The ham sandwich theorem asserts that, given bounded open sets
in
, there exists a hyperplane
that bisects each of these sets
, in the sense that each of the two half-spaces
on either side of the hyperplane captures exactly half of the volume of
. The shortest proof of this result proceeds by invoking the Borsuk-Ulam theorem.
A useful generalisation of the ham sandwich theorem is the polynomial ham sandwich theorem, which asserts that given bounded open sets
in
, there exists a hypersurface
of degree
(thus
is a polynomial of degree
such that the two semi-algebraic sets
and
capture half the volume of each of the
. (More precisely, the degree will be at most
, where
is the first positive integer for which
exceeds
.) This theorem can be deduced from the Borsuk-Ulam theorem in the same manner that the ordinary ham sandwich theorem is (and can also be deduced directly from the ordinary ham sandwich theorem via the Veronese embedding).
The polynomial ham sandwich theorem is a theorem about continuous bodies (bounded open sets), but a simple limiting argument leads one to the following discrete analogue: given finite sets
in
, there exists a hypersurface
of degree
, such that each of the two semi-algebraic sets
and
contain at most half of the points on
(note that some of the points of
can certainly lie on the boundary
). This can be iterated to give a useful cell decomposition:
Proposition 1 (Cell decomposition) Let
be a finite set of points in
, and let
be a positive integer. Then there exists a polynomial
of degree at most
, and a decomposition
into the hypersurface
and a collection
of cells bounded by
, such that
, and such that each cell
contains at most
points.
A proof is sketched in this previous blog post. The cells in the argument are not necessarily connected (being instead formed by intersecting together a number of semi-algebraic sets such as and
), but it is a classical result (established independently by Oleinik-Petrovskii, Milnor, and Thom) that any degree
hypersurface
divides
into
connected components, so one can easily assume that the cells are connected if desired. (Incidentally, one does not need the full machinery of the results in the above cited papers – which control not just the number of components, but all the Betti numbers of the complement of
– to get the bound on connected components; one can instead observe that every bounded connected component has a critical point where
, and one can control the number of these points by Bezout’s theorem, after perturbing
slightly to enforce genericity, and then count the unbounded components by an induction on dimension.)
Remark 1 By setting
as large as
, we obtain as a limiting case of the cell decomposition the fact that any finite set
of points in
can be captured by a hypersurface of degree
. This fact is in fact true over arbitrary fields (not just over
), and can be proven by a simple linear algebra argument (see e.g. this previous blog post). However, the cell decomposition is more flexible than this algebraic fact due to the ability to arbitrarily select the degree parameter
.
The cell decomposition can be viewed as a structural theorem for arbitrary large configurations of points in space, much as the Szemerédi regularity lemma can be viewed as a structural theorem for arbitrary large dense graphs. Indeed, just as many problems in the theory of large dense graphs can be profitably attacked by first applying the regularity lemma and then inspecting the outcome, it now seems that many problems in combinatorial incidence geometry can be attacked by applying the cell decomposition (or a similar such decomposition), with a parameter to be optimised later, to a relevant set of points, and seeing how the cells interact with each other and with the other objects in the configuration (lines, planes, circles, etc.). This strategy was spectacularly illustrated recently with Guth and Katz‘s use of the cell decomposition to resolve the Erdös distinct distance problem (up to logarithmic factors), as discussed in this blog post.
In this post, I wanted to record a simpler (but still illustrative) version of this method (that I learned from Nets Katz), namely to provide yet another proof of the Szemerédi-Trotter theorem in incidence geometry:
Theorem 2 (Szemerédi-Trotter theorem) Given a finite set of points
and a finite set of lines
in
, the set of incidences
has cardinality
This theorem has many short existing proofs, including one via crossing number inequalities (as discussed in this previous post) or via a slightly different type of cell decomposition (as discussed here). The proof given below is not that different, in particular, from the latter proof, but I believe it still serves as a good introduction to the polynomial method in combinatorial incidence geometry.
Let us begin with a trivial bound:
Lemma 3 (Trivial bound) For any finite set of points
and finite set of lines
, we have
.
The slickest way to prove this lemma is by the Cauchy-Schwarz inequality. If we let be the number of points
incident to a given line
, then we have
and hence by Cauchy-Schwarz
On the other hand, the left-hand side counts the number of triples with
. Since two distinct points
determine at most one line, one thus sees that the left-hand side is at most
, and the claim follows.
Now we return to the Szemerédi-Trotter theorem, and apply the cell decomposition with some parameter . This gives a decomposition
into a curve of degree
, and at most
cells
, each of which contains
points. We can then decompose
By removing repeated factors, we may take to be square-free.
Let us first deal with the incidences coming from the cells . Let
be the lines in
that pass through the
cell
. Clearly
and thus by the trivial bound
Now we make a key observation (coming from Bezout’s theorem: each line in can meet at most
cells
, because the cells
are bounded by a degree
curve
). Thus
and hence by Cauchy-Schwarz, we have
Putting all this together, we see that
Now we turn to the incidences coming from the curve . Applying Bezout’s theorem again, we see that each line in
either lies in
, or meets
in
points. The latter case contributes at most
incidences, so now we restrict attention to lines that are completely contained in
. The points in the curve
are of two types: smooth points (for which there is a unique tangent line to the curve
) and singular points (where
and
both vanish). A smooth point can be incident to at most one line in
, and so this case contributes at most
incidences. So we may restrict attention to the singular points. But by one last application of Bezout’s theorem, each line in
can intersect the zero-dimensional set
in at most
points (note that each partial derivative of
also has degree
), giving another contribution of
incidences. Putting everything together, we obtain
for any . An optimisation in
then gives the claim.
Remark 2 If one used the extreme case of the cell decomposition noted in Remark 1, one only obtains the trivial bound
On the other hand, this bound holds over arbitrary fields
(not just over
), and can be sharp in such cases (consider for instance the case when
is a finite field,
consists of all the points in
, and
consists of all the lines in
.)

23 comments
Comments feed for this article
18 February, 2011 at 8:36 am
mircea
Dear Prof. Tao,
Are there higher-dimensional versions of the Trotter-Szemeridi inequality? I ask this because the ham sandwich theorem seems not to be influenced by the dimension, whereas it would seem that the T-S theorem is.
Thank you!
18 February, 2011 at 9:10 am
Terence Tao
Yes (in principle, at least); and indeed, this is one of the advantages of the polynomial method over the other methods used to prove the Szemeredi-Trotter theorem (though the algebraic geometry can get more complicated in higher dimensions than the analysis of plane curves discussed in this post). Of course, since one can embed the plane in higher dimensions (or project a higher-dimensional incidence structure down to the plane), one needs to impose some additional non-degeneracy hypotheses in order to obtain a genuinely different higher-dimensional version of the theorem. One such theorem (in three dimensions, and assuming that not too many lines concentrate in a plane or regulus) is discussed at
17 September, 2023 at 6:14 am
Anonymous
Hello sir. I was wondering if this theorem had any applications in games (with ray tracing or binary space partition, even if very small?)
18 February, 2011 at 11:05 am
Gil Kalai
This is very nice! Can you deduce also the crossing lemma from the polynomial ham sandwitch theorem? (Or even the weak crossing lemma?)
There are some nice incidence and crossing problems in high dimension like: Conjecture: Let K be a 2-dimensional simplicial complex with e edges and t triangles. Then for every embedding of K into the number of crossing is at least . Problem: What is the maximum number of incidences between s lines and t planes in
. Problem: What is the maximum number of incidences between s lines and t planes in 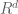 ?
?
(Those are taken from http://gilkalai.wordpress.com/2008/07/17/extermal-combinatorics-ii-some-geometry-and-number-theory/ )
18 February, 2011 at 11:14 am
Gil Kalai
(In the second problem it should be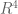 ; The crux for the first conjecture is to show that when you have a simplicial complex with
; The crux for the first conjecture is to show that when you have a simplicial complex with  edges and
edges and  triangles then when you embed it to
triangles then when you embed it to 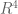 you must have at least one crossing.)
you must have at least one crossing.)
20 February, 2011 at 4:10 pm
Terence Tao
Dear Gil: I don’t see a way to use the polynomial method to bound crossing numbers in general, because the curves connecting points in a drawing are not restricted to be curves of bounded degree (and thus have no particular reason to be localised to only a small number of cells). Perhaps the method might be usable though to study crossings of restricted classes of drawings, such as drawings where the edges are straight line segments.
It would certainly be interesting to extend the method to higher-dimensional objects such as planes, but it seems that some non-trivial algebraic geometry would be needed to get sharp results.
21 February, 2011 at 11:43 am
Gil Kalai
Dear Terry: Doing it for the case of straight -line segments will already be interesting and having a crosing lemma for planar triangles in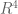 will be quite spectacular.
will be quite spectacular.
4 March, 2011 at 12:31 pm
Alfredo Hubard
I think this can be done, at least to some extent. If the curves representing the edges (or hyperedges) are algebraic, with bounded complexity. Check out theorem 18 in
http://arxiv.org/pdf/1102.1275v1
It is a version of the so called “same type lemma”, another way of saying “geometric Szemeredi” type result.
The application there is exactly of this type, a bound from below on the so called ” space crossing number” of straight line drawings of expanders in R3. The argument also gives good bounds for the crossing number of dense or random like graphs (in R2) or 2 complexes (in R4) or any other semialgebraic relation. If the graph (complex) is not dense nor random-like then something can be said with some classic extremal combinatorics but is rather weak
Some references:
Fox, Lafforgue, Gromov, Naor and Pach used another version of the same type lemma in a very similar way, I think that they also knew the lemma for semialgebraic relations.
Pach has several versions of it in different papers with different coauthors and applications, a very nice one to a Tverberg type theorem, Barany and Valtr coined the term (and proved one) “same type lemma” . All the versions are based on Ham Sandwiching, the particular ham sandwich type result used in BH11 and in FLGNP10 is the Yao-Yao partition, Lehec has a very nice proof the Yao Yao partition (which uses only the intermediate value theorem) and Alon was the first to use it in this combinatorial context.
I wonder if one can get the Katz-Guth decomposition in one stroke with the appropriate topological statement….
20 February, 2011 at 6:11 am
Nirman
Dear Prof. Tao,
are there any S-T type theorems for Projective spaces, maybe just planes, at least nicely behaved ones?
20 February, 2011 at 4:43 pm
Terence Tao
One can obtain projective Szemeredi-Trotter theorems from affine ones simply by covering projective space by copies of affine space. (One may lose some constant factors by doing so, but this is usually not a major concern in applications.)
20 February, 2011 at 9:32 pm
arnab
Thanks! Do you know if it is possible to obtain Beck’s theorem directly using this method, instead of going through Szemeredi-Trotter?
21 February, 2011 at 11:43 am
Weekly picks « Mathblogging.org developer.blog
[…] Friday you could also get some classic Terry Tao exposition, in this case, how to derive the Szemerédi-Trotter Theorem via the polynomial ham sandwich […]
24 February, 2011 at 6:31 am
Misha Rudnev
Dear Terry,
The question is more about the ham sandwich, but should extend, in principle, to ST-type results (where one should be careful as to what the “lines” are, etc.) In your Proposition 1, suppose d=3. Can one now replace R^3 with a three-dimensional manifold, which is “nicely”, by way of polynomials of bounded degree, embedded in some higher dimension, like say SO3 in R^9? Basically one would like to have a cell decomposition for a point set in a manifold, rather than the Euclidean space, with the estimates being controlled by Bezout, “as if” the manifold were R^3, as much as possible regardless of the dimension in which it is embedded.
Many Thanks,
Misha
24 February, 2011 at 6:39 am
Terence Tao
Yes, one can do this, either by randomly projecting, say, a 3-manifold in R^9 back down to R^3, performing the cell decomposition there, and pulling back, or else modifying the proof of the polynomial ham sandwich theorem (via Borsuk-Ulam) directly. In the latter case one has to (lower) bound the Hilbert function of the algebraic set one is working in, but there is an extensive literature on this function (at least in the bounded degree regime).
17 March, 2011 at 8:00 am
An incidence theorem in higher dimensions « What’s new
[…] In this paper we use the polynomial Ham Sandwich method of Guth and Katz (as discussed previously on this blog) to establish higher-dimensional versions of the Szemerédi-Trotter theorem, albeit […]
6 October, 2011 at 9:48 am
拓扑学奇趣之Borsuk-Ulam定理 « Fight with Infinity
[…] The Szemerédi-Trotter theorem via the polynomial Ham Sandwich […]
11 February, 2013 at 2:33 pm
Matthew Kahle
I am a little bit confused by the end of the argument “An optimization in $D$ then gives the claim.”
Optimizing for $D$ seems to yield something like $D \approx L^{-1/3} P^{2/3}$.
But then plugging in gives $$I(P,L) \ll |P|^{2/3}L^{2/3} + P.$$
This seems to prove the claim, but it is too strong. For example, consider the set of all lines through a single point.
11 February, 2013 at 11:43 pm
Terence Tao
Dear Matthew, one also has the constraint that D is a positive integer (in particular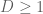 ) which means that the optimal value of D is more like
) which means that the optimal value of D is more like  .
.
30 June, 2013 at 5:48 pm
Polynomial partitioning: the basics (part 1) | Some Plane Truths
[…] We already discussed the Elekes-Sharir framework from item (i) here, here, and here (and due to several new developments, I might write more posts about this subject soon). This series of posts surveys the polynomial partitioning technique from item (ii). Basically, this is a technique for partitioning a -dimensional Euclidean space into a small number of “well behaved” cells. While the technique was originally introduced by Guth and Katz to solve the planar distinct distances problem, it already has several additional applications and extensions: a slightly improved upper bound for the three-dimensional unit distances problem (see here and here), improved bounds for various incidence problems (e.g., see here, here, and here), an alternative proof for the existence of a spanning tree with a low crossing number, and even a new range searching algorithm. Several recent works survey the basics of polynomial partitioning such as Zeev Dvir’s survey, Larry Guth’s lecture notes, this paper by Kaplan, Matoušek, and Sharir, and this blog post by Terry Tao. […]
25 October, 2013 at 7:48 am
Algebraic combinatorial geometry: the polynomial method in arithmetic combinatorics, incidence combinatorics, and number theory | What's new
[…] near-complete solution to the Erdos distance problem in the plane, and can be used to give a short proof of the Szemeredi-Trotter theorem. One of the aims of this survey is to try to present all of these disparate applications of the […]
3 December, 2013 at 8:34 pm
An incidence conjecture of Bourgain over fields of positive characteristic (with Hablicsek) | Quomodocumque
[…] In other words, the only way for a big family of lines to have lots of multiple intersections is for all those lines to be contained in a plane. (In the worst case where all the lines are in a plane, the incidences between points and lines are governed by the Szemeredi-Trotter theorem.) […]
7 October, 2019 at 11:01 pm
Configurations with many incidences and no triangles – Cosmin Pohoata
[…] theorem of Matousek (used also by Solymosi); see for instance these lecture notes of Guth or this blog post of Tao). Solymosi’s main observation is that under the additional assumption that the […]
19 May, 2022 at 5:43 pm
Freddie Manners
For what it’s worth, I think you can get away without the smooth points / singular points analysis in the final paragraph of the proof.
Certainly there can be at most lines
lines 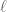 contained in
contained in  , as each one gives a divisor of
, as each one gives a divisor of 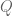 in
in ![\mathbb{R}[x,y]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BR%7D%5Bx%2Cy%5D&bg=ffffff&fg=545454&s=0&c=20201002) . So you can bound the number of incidences arising from these lines crudely by
. So you can bound the number of incidences arising from these lines crudely by  .
.
If this gets absorbed by the existing
this gets absorbed by the existing  and the the final optimization is not affected. If
and the the final optimization is not affected. If  , apply the theorem with the roles of
, apply the theorem with the roles of  and
and  reversed.
reversed.