Mathematicians study a variety of different mathematical structures, but perhaps the structures that are most commonly associated with mathematics are the number systems, such as the integers or the real numbers
. Indeed, the use of number systems is so closely identified with the practice of mathematics that one sometimes forgets that it is possible to do mathematics without explicit reference to any concept of number. For instance, the ancient Greeks were able to prove many theorems in Euclidean geometry, well before the development of Cartesian coordinates and analytic geometry in the seventeenth century, or the formal constructions or axiomatisations of the real number system that emerged in the nineteenth century (not to mention precursor concepts such as zero or negative numbers, whose very existence was highly controversial, if entertained at all, to the ancient Greeks). To do this, the Greeks used geometric operations as substitutes for the arithmetic operations that would be more familiar to modern mathematicians. For instance, concatenation of line segments or planar regions serves as a substitute for addition; the operation of forming a rectangle out of two line segments would serve as a substitute for multiplication; the concept of similarity can be used as a substitute for ratios or division; and so forth.
A similar situation exists in modern physics. Physical quantities such as length, mass, momentum, charge, and so forth are routinely measured and manipulated using the real number system (or related systems, such as
if one wishes to measure a vector-valued physical quantity such as velocity). Much as analytic geometry allows one to use the laws of algebra and trigonometry to calculate and prove theorems in geometry, the identification of physical quantities with numbers allows one to express physical laws and relationships (such as Einstein’s famous mass-energy equivalence
) as algebraic (or differential) equations, which can then be solved and otherwise manipulated through the extensive mathematical toolbox that has been developed over the centuries to deal with such equations.
However, as any student of physics is aware, most physical quantities are not represented purely by one or more numbers, but instead by a combination of a number and some sort of unit. For instance, it would be a category error to assert that the length of some object was a number such as ; instead, one has to say something like “the length of this object is
yards”, combining both a number
and a unit (in this case, the yard). Changing the unit leads to a change in the numerical value assigned to this physical quantity, even though no physical change to the object being measured has occurred. For instance, if one decides to use feet as the unit of length instead of yards, then the length of the object is now
feet; if one instead uses metres, the length is now
metres; and so forth. But nothing physical has changed when performing this change of units, and these lengths are considered all equal to each other:
It is then common to declare that while physical quantities and units are not, strictly speaking, numbers, they should be manipulated using the laws of algebra as if they were numerical quantities. For instance, if an object travels metres in
seconds, then its speed should be
where we use the usual abbreviations of and
for metres and seconds respectively. Similarly, if the speed of light
is
and an object has mass
, then Einstein’s mass-energy equivalence
then tells us that the energy-content of this object is
Note that the symbols are being manipulated algebraically as if they were mathematical variables such as
and
. By collecting all these units together, we see that every physical quantity gets assigned a unit of a certain dimension: for instance, we see here that the energy
of an object can be given the unit of
(more commonly known as a Joule), which has the dimension of
where
are the dimensions of mass, length, and time respectively.
There is however one important limitation to the ability to manipulate “dimensionful” quantities as if they were numbers: one is not supposed to add, subtract, or compare two physical quantities if they have different dimensions, although it is acceptable to multiply or divide two such quantities. For instance, if is a mass (having the units
) and
is a speed (having the units
), then it is physically “legitimate” to form an expression such as
, but not an expression such as
or
; in a similar spirit, statements such as
or
are physically meaningless. This combines well with the mathematical distinction between vector, scalar, and matrix quantities, which among other things prohibits one from adding together two such quantities if their vector or matrix type are different (e.g. one cannot add a scalar to a vector, or a vector to a matrix), and also places limitations on when two such quantities can be multiplied together. A related limitation, which is not always made explicit in physics texts, is that transcendental mathematical functions such as
or
should only be applied to arguments that are dimensionless; thus, for instance, if
is a speed, then
is not physically meaningful, but
is (this particular quantity is known as the rapidity associated to this speed).
These limitations may seem like a weakness in the mathematical modeling of physical quantities; one may think that one could get a more “powerful” mathematical framework if one were allowed to perform dimensionally inconsistent operations, such as add together a mass and a velocity, add together a vector and a scalar, exponentiate a length, etc. Certainly there is some precedent for this in mathematics; for instance, the formalism of Clifford algebras does in fact allow one to (among other things) add vectors with scalars, and in differential geometry it is quite common to formally apply transcendental functions (such as the exponential function) to a differential form (for instance, the Liouville measure of a symplectic manifold can be usefully thought of as a component of the exponential
of the symplectic form
).
However, there are several reasons why it is advantageous to retain the limitation to only perform dimensionally consistent operations. One is that of error correction: one can often catch (and correct for) errors in one’s calculations by discovering a dimensional inconsistency, and tracing it back to the first step where it occurs. Also, by performing dimensional analysis, one can often identify the form of a physical law before one has fully derived it. For instance, if one postulates the existence of a mass-energy relationship involving only the mass of an object , the energy content
, and the speed of light
, dimensional analysis is already sufficient to deduce that the relationship must be of the form
for some dimensionless absolute constant
; the only remaining task is then to work out the constant of proportionality
, which requires physical arguments beyond that provided by dimensional analysis. (This is a simple instance of a more general application of dimensional analysis known as the Buckingham
theorem.)
The use of units and dimensional analysis has certainly been proven to be very effective tools in physics. But one can pose the question of whether it has a properly grounded mathematical foundation, in order to settle any lingering unease about using such tools in physics, and also in order to rigorously develop such tools for purely mathematical purposes (such as analysing identities and inequalities in such fields of mathematics as harmonic analysis or partial differential equations).
The example of Euclidean geometry mentioned previously offers one possible approach to formalising the use of dimensions. For instance, one could model the length of a line segment not by a number, but rather by the equivalence class of all line segments congruent to the original line segment (cf. the Frege-Russell definition of a number). Similarly, the area of a planar region can be modeled not by a number, but by the equivalence class of all regions that are equidecomposable with the original region (one can, if one wishes, restrict attention here to measurable sets in order to avoid Banach-Tarski-type paradoxes, though that particular paradox actually only arises in three and higher dimensions). As mentioned before, it is then geometrically natural to multiply two lengths to form an area, by taking a rectangle whose line segments have the stated lengths, and using the area of that rectangle as a product. This geometric picture works well for units such as length and volume that have a spatial geometric interpretation, but it is less clear how to apply it for more general units. For instance, it does not seem geometrically natural (or, for that matter, conceptually helpful) to envision the equation as the assertion that the energy
is the volume of a rectangular box whose height is the mass
and whose length and width is given by the speed of light
.
But there are at least two other ways to formalise dimensionful quantities in mathematics, which I will discuss below the fold. The first is a “parametric” model in which dimensionful objects are modeled as numbers (or vectors, matrices, etc.) depending on some base dimensional parameters (such as units of length, mass, and time, or perhaps a coordinate system for space or spacetime), and transforming according to some representation of a structure group that encodes the range of these parameters; this type of “coordinate-heavy” model is often used (either implicitly or explicitly) by physicists in order to efficiently perform calculations, particularly when manipulating vector or tensor-valued quantities. The second is an “abstract” model in which dimensionful objects now live in an abstract mathematical space (e.g. an abstract vector space), in which only a subset of the operations available to general-purpose number systems such as or
are available, namely those operations which are “dimensionally consistent” or invariant (or more precisely, equivariant) with respect to the action of the underlying structure group. This sort of “coordinate-free” approach tends to be the one which is preferred by pure mathematicians, particularly in the various branches of modern geometry, in part because it can lead to greater conceptual clarity, as well as results of great generality; it is also close to the more informal practice of treating mathematical manipulations that do not preserve dimensional consistency as being physically meaningless.
— 1. The parametric approach —
In the parametric approach to formalising units and dimension, we postulate the existence of one or more dimensional parameters; for sake of discussion, let us initially use (representing the mass unit, length unit, and time unit respectively) for the dimensional parameters, though later in this discussion we will consider other sets of dimensional parameters. We will allow these parameters
to range freely and independently among the positive real numbers
, thus the parameter space (or structure group) here is given by the multiplicative group
. Later on, we will consider more general situations in which the parameter space is given by more general structure groups. (Actually, it would be slightly more natural to use a parameter space which was a torsor of the structure group, rather than the structure group itself; we discuss this at the very end of the post.)
We then distinguish two types of mathematical object in the “dimensionful universe”:
- Dimensionless objects
, which do not depend on the dimensional parameters
;
- Dimensionful objects
, which depend on the dimensional parameters
.
Similarly with “object” replaced by “number”, “vector”, or any other mathematical object. (Strictly speaking, with this convention, a dimensionless object is a degenerate special case of a dimensionful object; one could, if one wished, talk about strictly dimensionful objects in which the dependence of on
is non-constant.) Our conventions will be slightly different when we turn to dimensionful sets rather than dimensionful objects, but we postpone discussion of this subtlety until later.
The distinction between dimensionless and dimensionful objects is analogous to the distinction between standard and (cheap) nonstandard objects in (cheap) nonstandard analysis. However, whereas in nonstandard analysis the underlying parameter is usually thought of as an infinitely large parameter, in dimensional analysis the dimensional parameters
are usually thought of as neither being infinitesimally small or infinitely large, but rather a medium-sized quantity taking values comparable to those encountered in the physical system being studied.
A typical example of a dimensionful quantity is the numerical length of a physical rod
, in terms of a length unit which is
yards (say) long. For instance, if
is ten yards long, then
. Furthermore,
, since when
, the length unit is now
yards, i.e. a foot, and
is thirty feet long. More generally, we see that
Thus, a quantity which measures the numerical length of an object is a dimensionful quantity behaves inversely to the size of the length unit. More generally, let us say that a dimensionful numerical quantity has dimension
for some (dimensionless) exponents
if one has a proportionality relationship of the form
for some number . For instance, the speed of an object, measured in length units per time unit, where length unit is
yards long and the time unit is
seconds in duration, is a dimensionful quantity of dimension
. The presence of the negative signs in (1) may seem surprising at first, but this is due to the fact that (1) is describing the effect of a passive change of units rather than an active change of the object
.
(Note here one slight defect of this approach in modeling physical quantities, in that one has to select a preferred system of units (in this case, yards, seconds, and some unspecified mass unit) in order to interpret the parameters numerically. As mentioned above, one can avoid this by viewing the parameters as torsors rather than numbers; we will discuss this briefly at the end of this post.)
In the language of representation theory, the collection of dimensionful quantities of dimension is a weight space of the structure group
of weight
. One can indeed view dimensional analysis as being the representation theory of groups such as
, this viewpoint will become more prominent when we consider more general structure groups than
later in this section.
Note that with this definition, it is possible that some dimensionful quantities do not have any specific dimension , due to the dependence on
being more complicated than a simple power law relationship. To give a (contrived) example, the dimensionful quantity
does not have any specific dimension attached to it.
We can manipulate dimensionful quantities mathematically by applying any given mathematical operation pointwise for each choice of dimensional parameters . For instance, if
and
are two dimensionful numerical quantities, we can form their sum
by the formula
Similarly one can define ,
,
(if
is never vanishing),
,
, etc.. We also declare
if one has
for all
, and similarly declare
if one has
for all
, and so forth. Note that any law of algebra that is expressible as a universal identity will continue to hold for dimensionful quantities; for instance, the distributive law
holds for ordinary real numbers, and hence clearly also holds for dimensionful real numbers.
With these conventions, we now see a difference between dimensionally consistent and dimensionally inconsistent operations. If and
both have units
, then their sum
and difference
also has units
; but if
has units
and
has units
for some
, then the sum
or difference
, while still defined as a dimensionful quantity, no longrer has any single dimension. For instance, if one adds a length
to a speed
, one obtains a hybrid dimensionful quantity
which is not of the form (1). Similarly, applying a transcendental function
to a dimensionful quantity
will almost certainly generate a quantity with no specific dimension, unless the quantity
was actually dimensionless (in which case
will be dimensionless too, of course). On the other hand, dimensions interact very well with products and quotients: the product of a quantity of dimension
with a quantity of dimension
is a quantity of dimension
, and similarly for quotients.
Now we turn to equality. If two quantities have the same units
, then we see that in order to test the equality
of the two objects, it suffices to do so for a single choice of dimensional parameters
: if
for a single tuple
, then one has
for all
. Similarly for order relations such as
or
. In particular, if two quantities
have the same units, then we have the usual order trichotomy: exactly of
holds. In contrast, it is possible for two dimensionful quantities to be incomparable: for instance, using the quantities
and
from before, we see that none of the three statements
,
,
are true (which, in the dimensionful universe, means that they are valid for all choices of dimension parameters
): instead, we have
for
and
for
. Indeed, if
and
have different dimensions, we see that the equation
cannot hold at all, unless
and
both vanish. Thus we see that any non-trivial dimensionally inconsistent identity (in which the left and right-hand sides have different dimensions) can be automatically ruled out as being false.
A similar situation holds for inequality: if are strictly positive dimensionful quantities with different dimensions, then none of the statements
,
,
, or
can hold. (On the other hand, with our conventions, a strictly positive quantity is always greater than a strictly negative quantity, even when the dimensions do not match.) The situation gets more complicated though when dealing with quantities of hybrid dimension. For instance, the arithmetic mean-geometric mean inequality tells us that
for any two strictly positive dimensionful quantities , even if these quantities have different dimensions. For instance, if
has dimension
and
has dimension
, then the left-hand side
has dimension
, but the two terms
,
on the right-hand side have dimensions
and
respectively. But this inequality can still be viewed as dimensionally consistent, if one broadens the notion of dimensional consistency sufficiently. For instance, if
is the sum of
strictly positive quantities of dimension
for
and some
, and
is similarly the sum of
strictly quantities of dimension
for
and some
, it is an instructive exercise to show that an inequality of the form
or
can only hold if the convex hull of the
is contained in the convex hull of the
(and that equality
can only hold if the two sets
and
agree). Thus, for instance, (2) is dimensionally consistent in this generalised sense, because the exponent pair
associated to the left-hand side
lies in the convex hull of the exponent pairs
associated to the right-hand side
. On the other hand, this analysis helps explain why we almost never see such hybrid dimensional quantities appear in a physical problem, because while one can bound a positive quantity with a single dimension by a combination of positive quantities of different dimensions (as in (2)), the converse is not possible: one cannot bound a positive quantity of hybrid dimension by a quantity with a single dimension. As a consequence, if one is trying to establish an inequality
between two positive quantities of the same dimension by writing down a chain
of intermediate inequalities, one cannot have any of the intermediate quantities
be of hybrid dimension, as this will necessarily cause one of the inequalities in the chain to fail as soon as one attempts to bound a hybrid quantity by a non-hybrid quantity. Similarly if one wishes to prove an equality
instead of an inequality.
We have already observed that to verify a dimensionally consistent statement between dimensionful quantities, it suffices to do so for a single choice of the dimension parameters ; one can view this as being analogous to the transfer principle in nonstandard analysis, relating dimensionful mathematics with dimensionless mathematics. Thus, for instance, if
have the units of
,
, and
respectively, then to verify the dimensionally consistent identity
, it suffices to do so for a single choice of units
. For instance, one can choose a set of units (such as Planck units) for which the speed of light
becomes
, in which case the dimensionally consistent identity
simplifies to the dimensionally inconsistent identity
. Note that once we sacrifice dimensional consistency, though, we cannot then transfer back to the dimensionful setting; the identity
does not hold for all choices of units, only the special choice of units for which
. So we see a tradeoff between the freedom to vary units, and the freedom to work with dimensionally inconsistent equations; one can spend one freedom for another, but one cannot have both at the same time. (This is closely related to the concept of spending symmetry, which I discuss for instance in this post (or in Section 2.1 of this book).)
Thus far, we have only considered scalar dimensionful quantities: quantities which, for each choice of dimensional parameters , take values in a number system such as
. One can similarly consider vector-valued or matrix-valued dimensionful quantities, with only minor changes (though see below, when we consider coordinate systems to themselves be a dimensional parameter). We remark though that one could consider vectors in which different components have different dimensions. For instance, one could consider a four-dimensional vector
in which the first three components
have the dimension of length
, while the final component
has the dimension of time
.
Now we turn to the notion of a dimensionful set, which requires some care. We will define a dimensionful set to be a set of dimensionful objects
. Thus, for instance, the collection
of all dimensionful numbers of dimension
would be a dimensionful set; it is isomorphic to the reals
, because a dimensionful real number of a given dimension is entirely determined by its value for a single choice of parameters. But one should view the dimensionful sets
as
vary as being distinct copies of
. We say that a dimensionful set
of reals has dimension
if each element of
has this dimension.
Given a dimensionful set , one can evaluate it at any given choice
of parameters, by evaluating each point of
at this choice:
However, in contrast with the situation with dimensionful objects, a dimensionful set is not completely characterised by its evaluations
at each choice of parameters
. For instance, if one evaluates the dimensionful set
at any given
, one just gets the ordinary real numbers:
However, the sets and
are still distinct (indeed, they only intersect at the origin). The point is that membership of a dimensionful point
in a dimensionful set
is a global property rather than a local one; in order for
to lie in
, it is necessary that
for all
, but this condition is not sufficient (unless
and
have the same dimension, in which case it suffices to have
for just a single
).
Given two dimensionful sets , we define a dimensionful function
from
to
to be a family
of functions which maps points in
to points in
; thus, if
is a point in
, then the dimensionful object
defined by pointwise evaluation
is a point in . Thus, for instance, the squaring function
can be viewed both as a dimensionless function, and also as a function from
to
for any
. (Thus, when describing a dimensionful function
, it is not quite enough to specify the specific instantiations
of that function; one must also specify the dimensionful domain
and range
.) As another example, if
is a dimensionful quantity of some units
(representing amplitude) and
is a dimensionful quantity of units
(representing a time frequency), then the function
(thus
for all
) is a dimensional function from
to
.
A dimensionful function has instantiations
that scale according to the rule
for any and some dimensionless function
; conversely, every dimensionless function
creates a dimensionful function
in this fashion. As such, one can again transfer between the dimensionful and dimensionless settings when manipulating functions and objects, provided as before that all statements involved are dimensionally consistent.
An important additional operation available to dimensionful functions that is not available (in any non-trivial sense) to dimensionful scalars is that of integration. Given a dimensionful function on some one-dimensional dimensionful set
, one can form the integral
(assuming sufficient regularity and decay conditions on
and
, which we will not dwell on here) by the formula
One can verify that this integral is indeed a dimensionful quantity of dimension
. (One way to see this is to first verify the analogous claim for Riemann sums, and then to observe that the property of being a given dimension is a closed condition in the sense that it is preserved under limits.) In the opposite direction, the derivative
of this function, defined in the obvious fashion as
can be easily verified to be a dimensionful quantity of dimension . (As before, this can be seen by first considering Newton quotients and then taking limits.)
With this formalism, one can now use dimensional analysis to help test the truth of various estimates in harmonic analysis. Consider for instance the homogeneous Sobolev inequality
for all sufficiently nice functions (again, we will not dwell on the precise regularity needed here, as it is not the main focus of this post), for certain choices of exponents
and
, and a constant
that is independent of
. To dimensionally analyse this inequality, we introduce two dimensional parameters – a length unit
and an amplitude unit
– and view
as a function from
to
rather than from
to
; thus, by (3) (now using parameters
instead of
), we have
(As before, the exponents seem reversed from the more familiar rescaling , due to the fact that we are measuring change with respect to passive rescaling of units rather than an active rescaling of the function
.) We can then verify that
has dimension
,
has dimension
,
has dimension
, and so the left-hand side (4) of
has dimension
. A similar calculation (treating
as dimensionless) shows that the right-hand side of (4) has dimension
. If (4) holds for dimensionless functions, it holds for dimensionful functions as well (by applying the inequality to each instantiation of the dimensionful function); as the quantities in (4) are positive for non-trivial
, we conclude that (4) can only hold if we have the dimensional consistency relation
In fact, this condition turns out to be sufficient as well as necessary, although this is a non-trivial fact that cannot be proven purely by dimensional analysis; see e.g. these notes.
In a similar vein, one can dimensionally analyse the inhomogeneous Sobolev inequality
Using the same units as before, the left-hand side has dimension , and the right-hand side is a hybrid of the dimensions
and
, leading to the dimensional consistency relation
for this inequality, as a necessary condition for (5). (See also this blog post for an equivalent way to establish these conditions, using rescaled test functions instead of dimensional analysis; as mentioned earlier, the relation between these two approaches is essentially the difference between active and passive transformations.)
We saw earlier that hybrid inequalities (in which the right-hand side contains terms of different dimension) are not as useful or “efficient” as dimensionally pure inequalities (in which both sides have the same, single dimension). But it is often possible to amplify a hybrid inequality into a dimensionally pure one by optimising over all rescalings; see this previous blog post for a discussion of this trick (which, among other things, amplifies the inhomogeneous Sobolev inequality into the Gagliardo-Nirenberg inequality).
In all the above discussion, the dimensional parameters used (such as or
) were scalar quantities, taking values in the multiplicative group
, and representing units in one-dimensional spaces. But, when dealing with vector quantities, one can perform a more powerful form of dimensional analysis in which the dimensional parameters lie in a more general group (which we call the structure group of the dimensionful universe being analysed). Suppose for instance one wishes to represent a vector
in a three-dimensional vector space
. One could designate some basis
of this space
as a reference basis, so that
is expressible as some linear combination
, in which case one could identify
with the row vector
, and identify
with
. But one could instead represent
in some different basis
, where
is a
matrix (where, by an abuse of notation, we use
as shorthand for
), in which case one obtains a new decomposition
where the row vector is related to the original row vector
by the formula
where is the transpose of
. Motivated by this, we may take the matrix
as the dimensional parameter (taking values in the structure group
of invertible
matrices), and define a polar vector or type
tensor to be a dimensionful vector
taking values in the space
of three-dimensional row vectors and transforming according to the law (6). This is the three-dimensional analogue of a scalar quantity of dimension
(which, in the one-dimensional setting, is just a scalar parameter in
rather than an element of
). Indeed, one can view units as being simply the one-dimensional special case of coordinate systems. (As with previous transformation laws, the presence of the transpose inverse in (6) comes from the use of passive transformations rather than active ones.)
Now suppose we do not wish to model a vector in
, but rather a linear functional
on
. Using the standard basis
, one can identify
with the row vector
. Replacing that basis with
, we obtain a new row vector
, which is related to the original vector by the formula
We will call a dimensionful vector-valued quantity of the form (7) a covector or type
tensor. Thus we see that while polar vectors and covectors can both be expressed (for each choice of
) as an element of
, they transform differently with respect to coordinate change (coming from the two different right-actions of the structure group
on
given by (6), (7)) and so it is not possible for a vector and covector to be equal as dimensionful quantities (unless they are both zero). If one tries to add a non-zero vector to a non-zero covector, one still obtains a dimensionful quantity taking values in
, but it is no longer transforms according to a single group action such as (6) or (7), but is instead coming from a more complicated hybrid of two such actions. On the other hand, the dot product of a vector and a covector becomes a dimensionless scalar, whereas the dot product of a vector with another vector, or a covector with another covector, does not transform according to any simple rule. This makes the distinction between vectors and covectors well suited to problems in affine geometry, which by their nature transform well with respect to the action of
. (However, if the geometric problem involves concepts such as length and angles, which do not transform easily with respect to
actions, then the vector/covector distinction is much less useful.)
One can also assign dimensions to higher rank tensors, such as matrices, -vectors, or
-forms; the notation here becomes rather complicated, but is perhaps best described using abstract index notation. The dimensional consistency of equations involving such tensors then becomes the requirement in abstract index notation that the subscripts and superscripts on the left-hand side of a tensor equation must match those on the right-hand side, after “canceling” any index that appears as both a subscript and a superscript on one side. (Abstract index notation is discussed further in this previous blog post.)
Another type of dimensional analysis arises when one takes the structure group to be a Euclidean group such as or
, rather than
or (some power of)
. For instance, one might be studying Euclidean geometry in the Euclidean plane
, which one might identify with the Cartesian plane
by some reference isomorphism
(which can be viewed as a choice of origin, coordinate axes, orientation, and unit length on
), so that a given point
in the Euclidean plane
is associated to a Cartesian point
in
. If we let
denote a rigid motion of
(some combination of a translation, rotation, and/or reflection on
), this gives rise to a new isomorphism
, and a new Cartesian point
If we view as a dimensional parameter, we can then define a position vector to be a dimensionful quantity
taking values in
that transforms according to the law
for some . If, instead of considering the position of a single point
in the Euclidean plane, one considers the displacement
between two points
in that plane, a similar line of reasoning leads to the concept of a displacement vector, which would be a dimensionful quantity
taking values in
that transforms according to the law
where is the homogeneous portion of
(thus
is an orthogonal linear transformation on
, and
for all
). Thus we see a rigorous distinction between the concepts of position and displacement vector that one sometimes sees in introductory linear algebra or physics courses. Note for instance that one can add a position vector to a displacement vector to obtain another position vector, or a displacement vector to a displacement vector to obtain a further displacement vector, but when adding a position vector to another position vector, one obtains a new type of vector which is neither a position vector nor a displacement vector. (On the other hand, convex combinations of position vectors still give a position vector as output.) The dimensional analysis distinction between position and displacement vectors can be useful in situations in which the ambient plane
has no preferred origin, allowing for a clean action by the Euclidean group
(or at least the translation subgroup
).
A similar discussion can also be given in three-dimensions for the Euclidean group (or the orthogonal subgroup
); in addition to the position/displacement vector distinction, one can also distinguish polar vectors from axial vectors, leading in particular to the conclusion that the cross product of two polar vectors is an axial vector rather than a polar vector. Among other things, this helps explain why, in any identity involving cross products, such as the Hodge decomposition
of the three-dimensional Laplacian , either all terms have an even number of cross products, or all terms have an odd number of cross products.
In a similar vein, one can dimensionally analyse physical quantities in spacetime using the Poincaré group as the structure group, in which case the principle of special relativity can be interpreted as the assertion that all physical quantities transform cleanly with respect to this group action (as opposed to having a hybrid transformation law, or one which privileges a specific reference frame). Similarly, if one enlarges the structure group to the diffeomorphism group of spacetime, one recovers the principle of general relativity (though an important caveat here is that if the spacetime is topologically non-trivial, one needs to work with local coordinate charts (or atlases of such charts, and the structure group needs to be relaxed to a looser concept, such as that of a pseudogroup) rather than a single global coordinate chart, which greatly complicates the parametrisation space). Using a group of gauge transformations instead as the symmetry group leads to a mathematical framework suitable for gauge theory; and so forth.
In the preceding examples, the structure groups were all examples of continuous Lie groups: ,
,
, etc.. But even a discrete structure group can lead to a non-trivial capability for dimensional analysis. Perhaps the most familiar example is the use of the structure group
as the range of the dimensional parameter
, leading to two types of scalars: symmetric scalars
, which are dimensionless (so
), and antisymmetric scalars
, which transform according to the law
. A function
then transforms antisymmetric scalars to symmetric ones if the function is even, or to antisymmetric ones if the function is odd; this leads to the usual parity rules regarding combinations of even and odd functions, explaining for instance why in any trigonometric identity such as
the number of odd functions (sine, tangent, cotangent, and their inverses) in each term has the same parity. (Incidentally, this particular discrete structure group can be combined with continuous structure groups, giving rise to various mathematical structures used in the theory of supersymmetry in physics.)
— 2. The abstract approach —
The parameteric approach described above is essentially the one which is emphasised in physics courses, in which any mathematical representation of a physical object includes a description of how that representation transforms with respect to elements of the relevant structure group, so that in effect all coordinatisations of the object are considered simultaneously. However, in pure mathematics it is often more preferable to take a more abstract, “coordinate free” approach, in which explicit use of coordinates is avoided whenever possible, in order to keep the mathematical framework as close as possible to the underlying geometry or physics of the situation, and also in order to allow for easy generalisation to other contexts of mathematical interest in which coordinate systems become inconvenient to use (as we already saw in the case of general relativity on a topologically non-trivial situations, in which global coordinate systems had to be replaced by local ones), or completely unavailable (e.g. in studying more general topological spaces than manifolds). With this abstract, minimalistic approach, one models objects as elements of abstract structures in which only the bare minimum of operations (namely, the “geometric”, “physical”, or “dimensionally consistent” operations) are permitted, viewing any excess structure (such as coordinates) as superfluous ontological baggage to be discarded if possible.
We have already implicitly seen this philosophy when discussing the example of different coordinatisations of a three-dimensional vector space . One can simply forget about coordinatisations altogether, and view
as an abstract vector space
, with the only operations initially available on
being that of addition and scalar multiplication, which obey a standard set of compatibility axioms which we omit here. (Thus, for instance, the dot product of two vectors in
would be undefined, due to the lack of a canonical inner product structure on this space.) The dual space
of covectors is also a three-dimensional vector space, but because there is no canonical identification between
and
, there is no way (with only these minimal structural operations) to equate a vector to a covector, or to add a vector to a covector. Thus, in this framework, dimensionally inconsistent operations are not just inconvenient to use; they are impossible to write down in the first place (unless one introduces some non-canonical choices, such as an identification of
with
).
One can add or remove structures to this vector space , depending on the situation. For instance, if one wants to remove the preferred origin from the vector space, one can work instead with the slightly weaker structure of an affine space, in which no preferred origin is present. In order to recover the operations of Euclidean geometry, one can then place a Euclidean metric on the affine space; in some situations, one may also wish to add an orientation or a Haar measure to the list of structures. By adding or deleting such structures, one changes the group of isomorphisms of the space (or the groupoid of isomorphisms between different spaces in the same category), which serve as the analogue of the structure group in the parametric viewpoint. For instance, for a three-dimensional vector space with no additional structure, the group of isomorphisms is
(or more precisely, the group is isomorphic to this matrix group). Adding a Euclidean metric on this space reduces the group to
, but then deleting the origin increases it again to
, and so forth. In the Kleinian approach to geometry as described by the Erlangen program, the group of isomorphisms plays a primary role; indeed, one can view any given type of geometry (e.g. Euclidean geometry, affine geometry, projective geometry, spherical geometry, etc.) as the study of all structures on a given homogeneous space that are invariant with respect to the action of the group of isomorphisms.
Many foundational mathematical structures (e.g. vector spaces, groups, rings, fields, topological spaces, measure spaces, etc.) are routinely presented in this sort of abstract, axiomatic framework, without reference to explicit coordinates or number systems. (But there are some exceptions; for instance, the standard definition of a smooth manifold (or a complex manifold, etc.) makes reference to an altas of smooth coordinate charts, the standard definition of an algebraic variety or scheme makes reference to affine charts, and so forth.) One can apply the same abstract perspective to scalars, such as the length or mass of an object, by viewing these quantities as lying in an abstract one-dimensional real vector space, rather than in a copy of .
For instance, to continue the example of the system of dimensions from the previous section, we can postulate the existence of three one-dimensional real vector spaces
(which are supposed to represent the vector space of possible masses, lengths, and times, where we permit for now the possibility of negative values for these units). As it is physically natural to distinguish between positive and negative masses, lengths, or times, we endow these one-dimensional spaces with a total ordering (obeying the obvious compatibility conditions with the vector space structure), so that these spaces are ordered one-dimensional real vector spaces. However, we do not designate a preferred unit in these spaces (which would identify each of them with
).
We can then use basic algebraic operations such as tensor product to create further one-dimensional real vector spaces, without ever needing to explicitly invoke a coordinate system (except perhaps in the proofs of some foundational lemmas, though not in the statements of those lemmas). For instance, one can define to be the tensor product
of
and
, which can be defined categorically as the universal vector space with a bilinear product
(thus any other bilinear product
must factor uniquely through the universal bilinear product). Note that we can canonically place an ordering on this tensor product
by declaring the tensor product of two positive quantities to again be positive. Similarly, one can define
as the dual space to
(with a linear functional on
being positive if it is positive on positive values of
), define
as the tensor product of
and
, and so forth. This leads to a definition of
for any integers
(actually, to be pedantic, it leads to multiple definitions of
for each
, but these definitions can are canonically and naturally isomorphic to each other, and so by abuse of notation one can safely treat them as being a single definition). With a bit of additional effort (and taking full advantage of the one-dimensionality of the vector spaces), one can also define spaces with fractional exponents; for instance, one can define
as the space of formal signed square roots
of non-negative elements
in
, with a rather complicated but explicitly definable rule for addition and scalar multiplication. (Such formal square roots do occasionally appear naturally in mathematical applications; for instance, half-densities (formal square roots of measures) arise naturally in the theory of Fourier integral operators. However, when working with vector-valued quantities in two and higher dimensions, there are representation-theoretic obstructions to taking arbitrary fractional powers of units (though the double cover of orthogonal groups by spin groups does allow for spinor-valued quantities whose “dimension” is in some sense the square root of that of a vector).
If one views elements of as having dimension
then, operations which are dimensionally consistent are well-defined, but operations which are dimensionally inconsistent are not. For instance, one can multiply an element in
with an element in
to obtain a product in
, but one cannot canonically place this product in any other space
. One can compare two quantities
and
(i.e. decide if
,
, or
if they lie in the same spaces
, but not if they lie in different spaces (particularly if one is careful to keep the origins
of each of these vector spaces
distinct from each other). And so forth. Subject to the requirement of dimensional consistency, all the usual laws of algebra continue to hold; for instance, the distributive law
continues to hold as long as
have the same dimension. (The situation here is similar to that of a graded algebra, except that one does not permit addition of objects of different dimensions or gradings.) Thus, one expects many proofs of results that work in a dimensionless context to translate over to this abstract dimensionful setting. However, some results will not translate into this framework due to their dimensional inconsistency. For instance, the inequality (2) does not make sense if
lies in
and
lies in
, and similarly the inequality (5) does not make sense for
a nice function from
to
. (Note that the usual definitions of integral and dimension (as limits of Riemann sums and Newton quotients respectively) can be extended to this abstract dimensionful setting, so long as one keeps track of the dimensionality of all objects involved.) But if a statement is dimensionally consistent and can be proven in a dimensionless framework, then it should be provable in the abstract dimensionful setting as well (indeed, if all else fails, one can simply pick a set of coordinates to express all the abstract quantities here numerically, and then run the dimensionless argument). So, while the abstract framework is apparently less powerful than the parameterised framework due to the restricted number of operations available, in practice it can be a more useful framework to work in, as the operations that remain in the framework tend to be precisely the ones that one actually needs to solve problems (provided, of course, that one has chosen the right abstract formalism that is adapted to the symmetries of the situation).
It is possible to convert the abstract framework into the parametric one by making some non-canonical choices of a reference unit system. For instance, in the abstract dimensional system, after selecting a reference system of units
,
,
, one can then identify
with
by identifying
with
, so that any
gets identified with some real number
. For any
, one can then replace the units
with rescaled units
, which changes the identification of
with
, so that an element
is now identified with the real number
which is of course just (1). Thus we see that after selecting a reference unit system, one can convert an object which has dimension
in the abstract framework into an object
which has dimension
in the parametric framework; conversely, every object
that has dimension
in the parametric framework arises from a unique object
in the abstract framework (if one keeps the reference units
fixed). Similarly for sets of objects, or functions between such sets. Note though that objects in the parametric dimension that do not have a single dimension, but rather some hybrid of various dimensions, do not correspond to any particular object in the abstract setting, unless one performs some additional algebraic constructions in the latter setting, such as taking formal sums of spaces of different dimensionalities.
The need to select some arbitrary reference units in order to connect the abstract and parametric frameworks is a bit inelegant. One way to avoid this (which was alluded to previously) is to interpret
not as scalars in
, but rather as elements of the
-torsors
,
,
respectively. With this modification to the parametric framework, the reference units
can now be omitted. On the other hand, by turning the parameters
into abstractly dimensionful quantities instead of dimensionless scalars, one loses some of the power of the parametric model, namely the power to perform numerical operations even if they are dimensionally inconsistent, and so one may as well work entirely in the abstract setting instead.

88 comments
Comments feed for this article
4 February, 2018 at 8:31 pm
Ted
You say that one can define spaces with fractional exponents – is there a way to extend this construction to irrational exponents? Physical quantities with dimensions that are irrational powers of the base units come up as, e.g., the prefactors in two-point correlation functions for interacting conformal field theories.
2 March, 2018 at 7:43 pm
Anonymous
I’m still trying to read this article, which seems very fancy. I would have guessed that physical quantity was a pair (r,u) where r is a real number and u is an element of the free abelian group generated by the ground units (length, mass, time, etc.). I guess the addition rule (a,u)+(b,u) doesn’t work for things like temperatures though, which is why it is a torsor (modulo the discussion about absolute zero further up). Hmm.
16 October, 2018 at 2:55 pm
Ted
One slightly unfortunate aspect of considering dimensionful quantities as tensor products of 1D vector spaces is that the commutativity of multiplication is not very natural. We can’t simply promote naive products to tensor products, because then e.g. the unit (length*time) would be inequivalent to the unit (time*length). To remedy this, we need to e.g. fix some arbitrary ordering, e.g. that all the “length” basis vectors go to the left of all of the “time” basis vectors, which isn’t terribly natural.
24 October, 2018 at 7:53 am
Terence Tao
Well, in practice this is not a problem because there is a canonical isomorphism between the two different ways to take the tensor product of two vector spaces (and similarly for tensor products
between the two different ways to take the tensor product of two vector spaces (and similarly for tensor products  ,
,  of three spaces). So, up to the abuse of notation of identifying these two spaces, multiplication becomes commutative and associative again.
of three spaces). So, up to the abuse of notation of identifying these two spaces, multiplication becomes commutative and associative again.
4 October, 2019 at 7:24 am
Ashok M Dhareshwar
There is the project of establishing sound foundation for measurement by Krantz, Luce, Suppes and Tversky, which has resulted in a series of volumes entitled Foundations of Measurement. Is there any significant overlap between that project and your project of foundations of dimensional analysis?
10 June, 2020 at 5:29 pm
Josh Samani
Perhaps you’re already aware of this, but Whitney formalized dimensional analysis as well in “The mathematics of physical quantities: Part II: Quantity structures and dimensional analysis.”
21 July, 2020 at 1:19 pm
Mauricio Calvao
Sometimes (e. g. Gelfand & Fomin, “Calculus of variations”, Chap. 1, Sec. 2; or Kreiszig, “Introductory functional analysis with applications”, Chap. 2, Sec. 9, Prob. 6) people define a norm on the real vector space![C^1[a,b]](https://s0.wp.com/latex.php?latex=C%5E1%5Ba%2Cb%5D&bg=ffffff&fg=545454&s=0&c=20201002) of all real-valued functions
of all real-valued functions 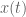 with closed interval
with closed interval ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=545454&s=0&c=20201002) for domain, via:
for domain, via:
where, of course,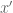 is the derivative of
is the derivative of  .
.
How can that be for cases where is *not* a dimensionless quantity, since then
is *not* a dimensionless quantity, since then  and
and 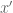 do not have the same dimensions and thus cannot be compared (added) at all? I do intuit this norm is trying, through the corresponding distance
do not have the same dimensions and thus cannot be compared (added) at all? I do intuit this norm is trying, through the corresponding distance  between two arbitrary functions in
between two arbitrary functions in ![C^1[a,b]](https://s0.wp.com/latex.php?latex=C%5E1%5Ba%2Cb%5D&bg=ffffff&fg=545454&s=0&c=20201002) , to formalize the notion that not only they have nearby values but also do so their derivatives; however it seems to miss the mark (just think of
, to formalize the notion that not only they have nearby values but also do so their derivatives; however it seems to miss the mark (just think of 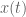 for
for  a position, with dimension of length, and
a position, with dimension of length, and  an instant, with dimension of time). If we modified the above norm so as to include a dimensional constant factor
an instant, with dimension of time). If we modified the above norm so as to include a dimensional constant factor  , with the same dimension of
, with the same dimension of  , in the second term of the RHS, then, dimensionally everything would now be fine. However, our results would seem to be dependent on this choice of scale, since these two norms would not be equivalent… Perhaps this is unavoidable and reflects the arbitrary choice of a tolerance degree in our comparison of the functions, taking into account their first derivatives. Of course, this issue is clearly generalized to
, in the second term of the RHS, then, dimensionally everything would now be fine. However, our results would seem to be dependent on this choice of scale, since these two norms would not be equivalent… Perhaps this is unavoidable and reflects the arbitrary choice of a tolerance degree in our comparison of the functions, taking into account their first derivatives. Of course, this issue is clearly generalized to ![C^k[a,b]](https://s0.wp.com/latex.php?latex=C%5Ek%5Ba%2Cb%5D&bg=ffffff&fg=545454&s=0&c=20201002) spaces.
spaces.
Thanks for any comments and clarifications.
29 July, 2020 at 1:08 pm
Terence Tao
You are correct that inhomogeneous norms such as the standard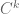 norms do not have a scale invariance and so cannot be assigned a single “dimension”; at best they can be viewed as a combination of expressions of different homogeneity, and as such they are sensitive to the choice of unit length scale. If one wants to proceed in a unit-independent fashion then the fix is as you say, to introduce a length scale parameter in front of the terms involving derivatives and to permit the inhomogeneous norms to depend on this choice of parameter. For instance, in this recent paper of mine I relied quite frequently on such scale-dependent
norms do not have a scale invariance and so cannot be assigned a single “dimension”; at best they can be viewed as a combination of expressions of different homogeneity, and as such they are sensitive to the choice of unit length scale. If one wants to proceed in a unit-independent fashion then the fix is as you say, to introduce a length scale parameter in front of the terms involving derivatives and to permit the inhomogeneous norms to depend on this choice of parameter. For instance, in this recent paper of mine I relied quite frequently on such scale-dependent 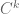 and Holder norms, see page 9.
and Holder norms, see page 9.
29 July, 2020 at 5:17 pm
Ted
What do you mean by “inhomogeneous norm”? I thought that “homogeneous” meant that scaling the vector by a scalar scales the norm by the absolute value of the same scalar (which, as far I can tell, is indeed the case for the $C^k$ norm), and that this property is part of the definition of a norm.
29 July, 2020 at 9:00 pm
Anonymous
All norms are homogeneous in that sense but when people call a norm homogeneous they mean the fourier multipliers that appear in the definition have the same homogeneity (eg. homogeneous H^2 has the symbol |\xi|^2 rather than 1+|\xi|^2)
29 July, 2020 at 9:07 pm
Anonymous
Correction: a better definition of homogeneous norm would be \|f(lambda x)\|=|lambda|^\alpha\|f\|
30 July, 2020 at 3:59 pm
Ted
Anonymous, in your second comment, do you mean $|f(\lambda x)| = |\lambda|^\alpha |f(x)|$, where $\lambda$ and $x$ are an arbitrary scalar and vector respectively and $f$ represents the norm? In that case, your equation is trivially true by definition for all norms, with $\alpha = 1$.
30 July, 2020 at 7:22 pm
Terence Tao
No; here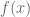 is shorthand for
is shorthand for  – a function in the function space of interest (e.g., a Holder space or a Sobolev space) – and
– a function in the function space of interest (e.g., a Holder space or a Sobolev space) – and 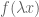 is shorthand for
is shorthand for 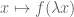 – a rescaled version of
– a rescaled version of  formed by dilating the underlying variable. For instance, if the function space in question is
formed by dilating the underlying variable. For instance, if the function space in question is 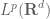 , then
, then  , thus the
, thus the 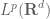 norm is homogeneous with exponent
norm is homogeneous with exponent 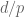 .
.
31 July, 2020 at 4:11 am
Ted
Ah, I see, thank you.
20 April, 2022 at 11:47 pm
Anonymous
I think this area lack something. deletion and annihilation can’t be expressed as minus – . $a_{-1} \oplus a = null $ such math symbol . But I don’t know is there any other people have done these work.
here is the paper about this area.
https://www.zhihu.com/question/273505468/answer/2425536318
27 March, 2024 at 5:12 am
Anonymous
Hello, I follow you from Turkey. I’m a civil engineer. As I was thinking about multiplication and understanding the nature of numbers, something started to confuse me. I realized that the multiplication we do when finding the area of a square is actually a magnitude in two different dimensions.
https://hizliresim.com/pejwcb5
First, consider a square with sides $4m$ long. The number $4$ and its unit is Meter. While one of these edges is on the x axis, the other is on the z axis. We multiply these edges $(4m)$, which are two different sizes, and an area emerges $16^{2}$. But the problem starts at this point. For example, if we multiply two 4m long edges on the x-axis, the result will be meaningless. Because we can multiply the length of 4m, which is the unit given by a number of the same size, by a number. For example, $(4m)cdot(4)$=16m Or we can multiply a 4m vector by a number. However, doesn’t $(4m)cdot(4m)$=undefined in one dimension? However, if there are two different sizes, I think these sizes are defined. So is there such a thing as dimensional warping? By size I don’t mean units. Thank you professor.