Next week (starting on Wednesday, to be more precise), I will begin my class on Perelman’s proof of the Poincaré conjecture. As I only have ten weeks in which to give this proof, I will have to move rapidly through some of the more basic aspects of Riemannian geometry which will be needed throughout the course. In particular, in this preliminary lecture, I will quickly review the basic notions of infinitesimal (or microlocal) Riemannian geometry, and in particular defining the Riemann, Ricci, and scalar curvatures of a Riemannian manifold. (The more “global” aspects of Riemannian geometry, for instance concerning the relationship between distance, curvature, injectivity radius, and volume, will be discussed later in this course.) This is a review only, in particular omitting any leisurely discussion of examples or motivation for Riemannian geometry; it is impossible to compress this subject into a single lecture, and I will have to refer you to a textbook on the subject for a more complete treatment (I myself am using the text “Riemannian geometry” by my colleague here at UCLA, Peter Petersen).
— Smooth manifolds —
Riemannian geometry takes place on smooth manifolds M of some dimension . Recall that a d-dimensional manifold (or d-manifold for short) M consists of the following structures:
- A topological space M (which for technical reasons we assume to be Hausdorff and second countable);
- An atlas of charts
, which are homeomorphisms from open sets
in M to open sets
in
, such that the
cover M.
We say that the manifold M is smooth if the charts define a consistent smooth structure, in the sense that the maps
is smooth (i.e. infinitely differentiable) on
for every
. One can then assert that a function
from M to another space with a smooth structure (e.g.
or
) is smooth if
is smooth on
for every
; a smooth map with an inverse which is also smooth is known as a diffeomorphism. The space of all smooth functions
is denoted
; this is a topological algebra over the reals. More generally, we have the algebra
for any open subset of M. (It is possible to view smooth manifolds more abstractly (and in a fully coordinate-independent fashion) by using the structure sheaf of algebras
to define the smooth structure, rather than the atlas of charts, but we will not need to take this perspective here.)
Remark 1. The most intuitive way to view manifolds is from an extrinsic viewpoint: as subsets of some larger-dimensional space (e.g. viewing curves as subsets of the plane, surfaces as subsets of a Euclidean space such as ). While every smooth manifold can be viewed this way (thanks to the Whitney embedding theorem), we will in fact not use the extrinsic perspective at all in this course! Instead, we will rely exclusively on the intrinsic perspective – by studying the various structures on a smooth manifold M purely in terms of objects that can be defined in terms of the atlas. In fact, once we set up the most basic such structure – the tangent bundle – we will often not use the atlas directly at all (thus working in a “coordinate-free” fashion). However, the “local coordinates” provided by the charts in an atlas will be useful for computations at various junctures.
Remark 2. It is a surprising and unintuitive fact that a single topological manifold can have two distinct smooth structures which are not diffeomorphic to each other! This is most famously the case for 7-spheres , giving rise to exotic spheres. However, in the case of 3-manifolds – which is the focus of this course – all smooth structures are diffeomorphic (a result of Munkres and Whitehead; see also Smale for higher-dimensional variants), and so this subtlety need not concern us.
[Aside: I was unable to find the relevant reference of Smale – does anyone know it?]
Remark 3. As is commutative, we will multiply by functions in this space on the left or on the right interchangeably. In noncommutative geometry, this algebra is replaced by a noncommutative algebra, and one has to take substantially more care with the order of multiplication, but we will not use noncommutative geometry here.
We will be interested in various vector bundles over a smooth manifold M. A vector bundle V is a collection of (real) vector spaces of a fixed dimension k (the fibres of the bundle) associated to each point
, whose disjoint union
can itself be given the structure of a smooth (d+k-dimensional) manifold, in such a way that for all sufficiently small neighbourhoods U of any given point x, the set
has a trivialisation, i.e. there is a diffeomorphism between
and
, with each fibre
being identified in a linearly isomorphic way with the vector space
. A (global) section of a vector bundle V is a smooth map
such that
for every
. The space of all sections is denoted
; it is a vector space over
, and furthermore is a module over
. We will sometimes also be interested in local sections
on some open subset U of M; the space of such sections (which form a module over
) will be denoted
. All of the discussion below on the global manifold M can be easily adapted to local open sets U in this manifold (indeed, one can interpret U itself as a manifold); as all our computations will be entirely local (and because of the ready availability of smooth cutoff functions), the theory on M and the theory on U will be completely compatible.
Example 1. The space can be canonically identified with the space of sections
of the trivial line bundle
.
In Riemannian geometry, the most fundamental vector bundle over a manifold M is the tangent bundle TM, defined by letting the tangent space at a point
be the space of all tangent vectors in M at x. A tangent vector
can be defined as a vector which can be expressed as the (formal) derivative
of some smooth curve
which passes through x at time zero, thus
. One can express these tangent vectors concretely by using any chart that covers x.
To be somewhat informal, given any point and tangent vector
, one can define a trajectory of points
for all “infinitesimal” t, which is only defined up to an error of
(as measured, for instance, in some coordinate chart), but whose derivative at
is equal to v. Thus, while the global manifold M need not have any reasonable notion of vector addition, we do have this infinitesimal notion of translation by a tangent vector which is well-defined up to second-order errors.
Given a tangent vector and a smooth function
, we can define the directional derivative
by the formula
(1)
(or, a bit more formally, for any curve
with
and
). This is a linear functional on
which annihilates constants and obeys the Leibniz rule
. (2)
Conversely, one can define the tangent space to be the space of all linear functionals on
with the above two properties, though we will not need to do so here.
A section of M is known as a vector field; it assigns a tangent vector
to each point
. A vector field X determines a first-order differential operator
, defined by setting
. From (2), we see that
is a derivation, i.e. it is linear over
and obeys the Leibniz rule
. (3)
Conversely, one can easily show that every derivation on arises uniquely in this manner. This provides a convenient means to define new types of vector fields. For example, if X and Y are two vector fields, one can easily see (from (3)) that the commutator
is also a derivation, and must thus be given by another vector field [X,Y], thus
(4)
for all vector fields X, Y and all scalar fields f.
Example 2. Suppose we have a local coordinate chart . The standard first-order differential operators
induced by the coordinates
on
can be viewed as vector fields, and pulled back via
to vector fields
on U. These in fact form a frame for U since they span the tangent space at every point. Since
and
commute in
, we see that
.
Exercise 1. Show that the map endows the space
of vector fields with the structure of an abstract Lie algebra. Also establish the Leibniz rule
(5)
for all and
.
Various operations on finite-dimensional vector spaces generalise easily to vector bundles. For instance, every finite-dimensional vector space V has a dual , and similarly every vector bundle V also has a dual bundle
, whose fibres
are the dual to the fibres
of V; one can also view
as the space of
-linear functionals from V to
. Similarly, given two vector bundles
over M, one can define the direct sum
, the tensor product
, the space
of fibre-wise linear transformations from V to W, the symmetric powers
and exterior powers
, and so forth. The construction of all of these concepts is straightforward but rather tedious, and will be omitted here.
Applying these constructions to the tangent bundle TM, one gets a variety of useful bundles for doing Riemannian geometry:
- The bundle
is the cotangent bundle; elements of
are cotangent vectors.
- Sections of
are known as k-forms.
- Sections of
are known as rank (k,l) tensor fields, and individual elements of this bundle are rank (k,l) tensors. Many tensors of interest obey various symmetry or antisymmetry properties, for instance k-forms are totally anti-symmetric rank (0,k) tensors. (To fully enumerate the various symmetry properties available to tensors is essentially equivalent to the finite-dimensional representation theory of the permutation group, which is a beautiful and important subject but will not be discussed here.)
It is convenient to use abstract index notation, denoting rank (k,l) tensor fields using k superscripted Greek indices and l subscripted Greek indices, thus for instance denotes a rank (1,3) tensor. One should think of these indices as placeholders; if one chooses a frame
for the tangent bundle (i.e. a collection of vector fields which form a basis for the tangent space at every point), which induces the associated dual frame
for the cotangent bundle, then this notation can be viewed as describing the coefficients of the tensor in terms of the basis generated by such frames, thus for instance
. (6)
But it is perhaps better to view a tensor such as as existing independently of any choice of frame, in which case the labels
are abstract placeholders.
Example 3. We continue Example 2. A local coordinate chart generates a (local) frame
with an associated dual frame
. These frames can be slightly easier to work with for computations than general frames, because we automatically have
as already noted in Example 2. On the other hand, it is often convenient to work in frames that don’t come from coordinate charts in order to obtain other good properties; in particular, it is very convenient to work in orthonormal frames, which are usually unavailable if one restricts attention to frames arising from coordinate charts.
We use the usual (and very handy) Einstein summation convention: repeated indices (with each repeated index appearing exactly once as a superscript and once as a subscript) are implicitly summed over a choice of frame (the exact choice is not important). For instance, the rank (0,4) tensor is defined to be the tensor which is given by the formula
(7)
for any choice of frame (one can easily verify that this definition is independent of the choice of frame). We will also apply this summation convention when the Greek labels are replaced with concrete counterparts arising from a frame, thus for instance we can now abbreviate (6) as
. (6′)
— Connections —
We have seen that vector fields allow us to differentiate scalar functions
to obtain a differentiated function
. Furthermore, this concept obeys the Leibniz rule (3), and is linear over
in X, or in other words
(8)
for all and
. As a consequence, one can interpret
as a
-linear functional on
, which is identified with a section
of the cotangent bundle, thus
.
Now suppose one wants to differentiate , where
is now a section of a bundle V. It turns out that there is now more than one good notion of differentiation. Each such notion can be formalised by the concept of a (linear) connection:
Definition 1. A connection
on a bundle V is an assignment of a section
(the covariant derivative of f in the direction X via the connection
) to each vector field
and section
, in such a way that
is bilinear in f and X, that the Leibniz rule (3) is obeyed for
and
(or vice versa), and the linearity rule (8) is obeyed for all
and
.
If
is such that
for all vector fields X, we say that f is parallel to the connection
.
A connection on the tangent bundle TM is known as an affine connection.
Remark 4. Informally, a connection assigns an infinitesimal linear isomorphism (the parallel transport map) to each infinitesimal tangent vector
, in a manner which is linear in v for fixed x. The connection between this informal definition and the above formal one is given by the formula
. One can make this informal definition more precise (e.g. using non-standard analysis) but we will not do so here. An alternate definition of a connection is as a complementary subbundle to the vertical bundle
in TV, known as a horizontal bundle, obeying some additional linearity conditions in the vertical variable.
Once one has a connection on a bundle V, one automatically can define a connection on the dual bundle and more generally on tensor powers
, by enforcing all possible instances of the Leibniz rule, e.g.
(9)
for all rank (2,1) tensors f and rank (1,1) tensors g. (It is a straightforward but tedious task to verify that all the Leibniz rules are consistent with each other, and that (9) and its relatives uniquely define a connection on every tensor power of V.) In particular, any connection on the tangent bundle (which is the case of importance in Riemannian geometry) naturally induces a connection on the cotangent bundle and the bundle of rank (k,l) tensors.
Here it is important to note that the indices are abstract, rather than corresponding to some frame: for instance, if is a connection on the tangent bundle TM, then after choosing a frame
, it is usually not the case that the coefficient
of a vector field
at a is equal to the derivative
of that component of f. Instead, one has a relationship of the form
(10)
where for each , the Christoffel symbol
of the connection relative to the frame
is a smooth function on M. It is important to note that Christoffel symbols are not tensors, because the expression
turns out to depend on the choice of frame.
Using the Leibnitz rule repeatedly, it is not hard to use (10) to give a formula for the components of derivatives of other tensors, e.g.
(11)
for any 1-form ,
(12)
for any rank (0,2) tensor g, and so forth.
We have remarked that Christoffel symbols are not tensors. On the other hand, because is linear in X, we can legitimately define a tensor field
, which is a section of
, thus
. It is also possible to express the difference of two connections as a tensor:
Exercise 2. Let be two connections on TM. Show that there exists a unique rank (1,2) tensor
such that
(13)
for all vector fields . Now interpret the Christoffel symbol
of a connection
on TM relative to a frame
as the difference
of that connection with the flat connection
induced by the trivialisation of the tangent bundle induced by that frame.
Let be a connection on TM. We say that this connection is torsion-free if we have the pleasant identity
(14)
(cf. Clairaut’s theorem) for all scalar fields , or in other words that the Hessian
of f is a symmetric rank (0,2) tensor.
Exercise 3. Show that is torsion-free if and only if
(15)
for all vector fields X, Y (or in coordinate-free notation, ).
Remark 5. Roughly speaking, the torsion-free connections are those which have a good notion of an infinitesimal parallelogram with corners for some infinitesimal t, such that each edge is the parallel transport of the opposing edge to error
. (Without the torsion-free hypothesis, the error is merely
.)
It would be nice if (14) extended to tensor fields f. This is true for flat connections, but false in general. The defect in (14) for such fields is measured by the curvature tensor of the connection
, defined by the formula
(16)
for all vector fields X,Y,Z (cf. (4)). One easily sees that R is indeed a section of and can thus be viewed as a rank (1,3) tensor.
Exercise 4. If is a torsion-free connection on TM, and
is the tensor form of the curvature R, defined by requiring that
, (17)
then show that
(18)
for all vector fields . What is the analogue of (18) if
is replaced by a rank (k,l) tensor?
Connections describe a way to transport tensors as one moves from point to point in the manifold. There is another way to transport tensors, which is induced by diffeomorphisms of the base manifold; this transportation procedure maps points
to points
, maps tangent vectors
to tangent vectors
(defined by requiring that the chain rule
hold for all curves
) and then maps other tensors in the unique manner consistent with the tensor operations (e.g.
). This procedure is important for describing symmetries of tensor fields (consider, for instance, what it means for the vector field
in
to be invariant under rotations around the origin). To relate this diffeomorphism transport to infinitesimal differential geometry, though, we have to look at an infinitesimal diffeomorphism, which we can view as the derivative
of a smoothly varying family
of diffeomorphisms, with
equal to the identity. By chasing all the definitions we see that
is just a vector field X. The infinitesimal rate of change
of a tensor field v under this diffeomorphism is known as the Lie derivative
of v with respect to the vector field X (it does not depend on any aspect of
other than its infinitesimal vector field). On scalars f, it agrees with directional derivative
, (19)
while on vector fields Y, it agrees with the commutator:
, (20)
and its action on all other tensors can be given by the Leibniz rule (as is the case for connections). It should be emphasised, though, that the Lie derivative is not a connection, because it is not linear (over ) in X;
in general.
— Riemannian manifolds and curvature tensors —
We now specialise our attention from smooth manifolds to our main topic of interest, namely Riemannian manifolds. Informally, a Riemannian manifold is a manifold equipped with notions of length, angle, area, etc. which are infinitesimally isomorphic at every point to the corresponding notions in Euclidean space. In Euclidean space, all these geometric notions can be defined in terms of a positive definite inner product, and Riemannian manifolds are similarly founded on a positive definite Riemannian metric.
Definition 2. A Riemannian manifold (M,g) is a smooth manifold M, together with a Riemannian metric
on M, i.e. a section of
which is positive definite in the sense that
is a positive-definite inner product on
for every point x.
We now use the metric g to build several other tensors of interest. Firstly, we have the inverse metric , which is the unique rank (2,0) tensor that inverts the (0,2) tensor g in the sense that
is the identity section of
; this tensor is also symmetric and positive-definite. One can use these tensors to raise and lower the indices of other tensors; for instance, given a rank (0,2) tensor
, one can define the rank (1,1) tensors
and
and the rank (2,0) tensor
. We will generally only use these conventions when there is enough symmetry that there is no danger of ambiguity.
Remark 6. All Riemannian manifolds can be viewed extrinsically (locally, at least) as subsets of a Euclidean space, thanks to the famous Nash embedding theorem. But we will not need this extrinsic viewpoint in this course.
After the metric, the next fundamental object in Riemannian geometry is the Levi-Civita connection.
Fundamental theorem of Riemannian geometry. Let (M,g) be a Riemannian manifold. Then there exists a unique affine connection
(which is known as the Levi-Civita connection) which is torsion-free and respects the metric g in the sense that
.
Exercise 5. Prove this theorem. (Hint: one can either (a) use abstract index notation and study expressions such as , (b) use coordinate-free notation and study expressions such as
, or (c) use local coordinates (e.g. use a frame
arising from a chart
as in Example 2) and work with the Christoffel symbols
. It is instructive to do this exercise in all three possible ways in order to appreciate the equivalence (and relative advantages and disadvantages) between these three perspectives.
Geometrically, the condition asserts that parallel transport by the Levi-Civita connection is an isometry. At a computational level, it means (in conjunction with the Leibnitz rule) that covariant differentiation using the Levi-Civita connection commutes with the raising and lowering operations, for instance given a vector field
we have
(21)
and so we may safely use raising and lowering operations in the presence of Levi-Civita covariant derivatives without much risk of serious error. We can also raise and lower the covariant derivative itself, defining
. (22)
This leads to the covariant Laplacian (or Bochner Laplacian)
(23)
defined on all tensor fields (for instance, when applied to scalar fields it becomes the trace of the Hessian, and is known as the Laplace-Beltrami operator). When applied to non-scalar fields, the covariant Laplacian differs slightly from the Hodge Laplacian (or Laplace-de Rham operator) by a lower order term which is given by the Weitzenböck identity.
As discussed earlier, all connections on TM have a curvature tensor in . The curvature of the Levi-Civita connection is known as the Riemann curvature tensor
, thus
. (24)
One also writes in co-ordinate free notation by defining
for vector fields X,Y,Z by the formula
(24′)
or equivalently as .
Because respects g, one eventually deduces from (24) and the Leibniz rule that
is skew-adjoint in the
indices:
. (25)
It is also clearly skew-symmetric in the indices. Also, from the analogue of (24) for 1-forms, i.e.
. (24”)
and the torsion-free nature of the connection, we have
(26)
for all scalar fields f. Cyclically summing this in we obtain the first Bianchi identity
. (27)
Exercise 6. Show that the above three symmetries of imply that
is a self-adjoint section of
, and that these conditions are in fact equivalent in three and fewer dimensions. (The claim fails in four and higher dimensions; see comments.)
Exercise 7. By differentiating (24) and cyclically summing, establish the second Bianchi identity
Exercise 8. Show that a Riemannian manifold (M,g) is locally isomorphic (as Riemannian manifolds) to Euclidean space if and only if the Riemann curvature tensor vanishes. (Hint: one direction is easy. For the other direction, the quickest way is to apply the Frobenius theorem to obtain a local trivialisation of the tangent bundle which is flat with respect to the Levi-Civita connection.) This illustrates the point that the Riemann curvature captures all the local obstructions that prevent a Riemannian manifold from being flat. (Compare this situation with the superficially similar subject of symplectic geometry, in which Darboux’s theorem guarantees that there are no local obstructions whatsoever to a symplectic manifold being flat.)
The Riemann curvature measures the “infinitesimal monodromy” of parallel transport. For our applications we will need to study a slightly different curvature, the Ricci curvature , which measures how much the volume-radius relationship on infinitesimal sectors has been distorted from the Euclidean one. (This will not be obvious presently, as we have not yet defined the volume measure
on a Riemannian manifold.) It is defined as the trace of the Riemannian tensor, or more precisely as
(One could also contract other indices than these, but due to the various symmetry properties of the Riemann tensor, one ends up with essentially the same tensor as a consequence.) We also write for
when X, Y are vector fields. The symmetries of
easily imply that
is a symmetric rank (2,0) tensor – just like the metric g! This observation will of course be vital for defining Ricci flow later. (This observation, as well as a similar observation for the stress-energy tensor, was also decisive in leading Einstein to the equations of general relativity, but that’s a whole other story.)
We can take the trace of the Ricci tensor to form the scalar curvature
up to normalisations, R can also be viewed as the trace of the Riemann tensor (viewed as a section of ). The scalar curvature measures how the relationship of volume of infinitesimal balls to their radius is distorted by the geometry.
The relationship between the Riemannian, Ricci, and scalar curvatures depends on the dimension:
- In one dimension, all three curvatures vanish; there are no degrees of freedom.
- In two dimensions, the Riemannian and Ricci curvatures are just multiples of the scalar curvature (by some tensor depending algebraically on the metric); there is only one degree of freedom.
- In three dimensions, the Riemann tensor is a linear combination of the Ricci curvature (see also Exercise 9 below). On the other hand, the scalar curvature does not control Ricci (or Riemann); the Ricci tensor contains an additional trace-free component. (However, once we start evolving by Ricci flow, we shall see that the Hamilton-Ivey pinching phenomenon will allow us to use the scalar curvature to mostly control Ricci and hence Riemann near singularities.)
- In four and higher dimensions, the Riemann tensor is not fully controlled by the Ricci curvature; there is an additional component to the Riemann tensor, namely the Weyl tensor. Similarly, the Ricci curvature is not fully controlled by the scalar curvature.
Exercise 9. (Ricci controls Riemann in three dimensions) In three dimensions, suppose that the (necessarily real) eigenvalues of the Riemann curvature at a point x (viewed as an element of ) are
. Show that the eigenvalues of the Ricci curvature at x (viewed as an element of
are
. Conclude in particular that
(31)
where we endow the (fibres of the) spaces and
with the Hilbert (or Hilbert-Schmidt) structure induced by the metric g.
Remark 7. The fact that Ricci controls Riemann in three dimensions, without itself degenerating into scalar curvature or zero, seems to explain why Ricci flow is especially powerful in three dimensions; it is still useful, but harder to work with, in two dimensions, useless in one dimension, and too weak to fully control the geometry in four and higher dimensions. It seems to me that the special nature of three dimensions stems from the fact that it is the unique number of dimensions in which 2-forms (which are naturally associated with curvature) are Hodge dual to vector fields (as opposed to scalars, or to higher-rank tensors); this is the same special feature of three dimensions which gives us the cross product (as opposed to the more general wedge product).
Because of the variety of curvatures, there are various notions of what it means for a manifold to have “non-negative curvature” at some point.
Definition 3. Let x be a point on a Riemannian manifold (M,g). We say that x has
- non-negative scalar curvature if
;
- non-negative Ricci curvature if
as a quadratic form on TM, i.e.
for all vectors
;
- non-negative sectional curvature if
for all vectors
;
- non-negative Riemann curvature if
as a quadratic form on
, thus
for all two-forms
.
It is not hard to show that, in arbitrary dimension, 4. implies 3. implies 2. implies 1. In one dimension, these conditions are vacuously true; in two dimensions; these conditions are all equivalent; and in three dimensions, non-negative Riemann curvature is equivalent to non-negative sectional curvature (because every 2-form is the wedge product of two one-forms in this case) but these conditions are otherwise distinct. In four and higher dimensions all of these conditions are distinct. One can also define the analogous notions of positive curvature (or negative curvature, or non-positive curvature) in the usual manner.
[Geometrically, positive scalar curvature means that infinitesimal balls have slightly less volume than in the Euclidean case; positive Ricci curvature means that infinitesimal sectors have slightly less volume than in the Euclidean case; and positive sectional curvature means that all infinitesimally geodesic two-dimensional surfaces have positive gaussian curvature. I don’t know of a geometrically simple way to describe positive Riemann curvature.]
A couple lectures from now, we shall compute these curvatures explicitly in a number of model cases (such as that of a homogeneous space). For now, we give a “cartoon” or “schematic” description of these curvatures when viewed in some local coordinate system , using the associated frame
as in Example 2 to express all tensors as arrays of numbers. Writing
, we thus schematically have the following relationships:
- The Christoffel symbols
are schematically of the form
. Thus a covariant derivative
of a tensor w looks schematically like
, and the Laplacian
looks like
.
- The Riemann curvature tensor
and the Ricci curvature tensor
schematically take the form
.
- The scalar curvature R schematically takes the form
. (Thus the scalar curvature has the same scaling as the Laplacian.)
Remark 8. Note how in all of these expressions, the “number of derivatives” and “number of g’s” stays fixed among all terms in a given expression. This can be viewed as an example of dimensional analysis in action, and is useful for catching errors in manipulations with these sorts of expressions. From a more representation-theoretic viewpoint, what is going on is that all of the above expressions have constant weight with respect to the joint (commuting) actions of the dilation operation on the underlying coordinate chart (which essentially controls the number of derivatives
that appear) and the homogeneity operation
(which, naturally enough, controls the number of g’s that appear).
[Update, Mar 27: more remarks added; various corrections.]

51 comments
Comments feed for this article
27 March, 2008 at 3:01 am
Pedro Lauridsen Ribeiro
The contribution of Smale to the uniqueness of the diffeomorphism
class of differentiable structures of S^3 is actually Theorem J (cf. p.
393) of his landmark paper on the proof of the Poincare conjecture in
higher dimensions (S. Smale, “Generalized Poincare Conjecture in
Dimensions Greater than Four”, Ann. Math. 74 (1961) 391-406).
There, he proves that there is a finite number of diffeomorphism
classes of differentiable structures in S^n, n odd, but when it comes
to the actual uniqueness for S^3, he quotes the result of Munkres.
27 March, 2008 at 7:53 am
Terence Tao
Dear Pedro: thanks for clarifying that point!
27 March, 2008 at 8:40 am
davidspeyer
I am tremendously excited about this series of posts. Therefore, I will celebrate with some nitpicks and questions. :)
Regarding Exercise 6: In dimension four and above, the first Bianchi identity and the skew symmetry in ,
,  are strictly stronger conditions on a
are strictly stronger conditions on a 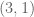 tensor then being a self-adjoint operator from
tensor then being a self-adjoint operator from  to itself.
to itself.
To see this, work with . Then the symmetries you refer to are
. Then the symmetries you refer to are
The condition that be a self-adjoint map from
be a self-adjoint map from  to itself is condition (1) combined with
to itself is condition (1) combined with
Consider the case where is antisymmetric in all its indices. This satisfies (1) and (3) (the latter because the permutation 3412 is even) but not (2).
is antisymmetric in all its indices. This satisfies (1) and (3) (the latter because the permutation 3412 is even) but not (2).
The symmetries above state that lies in
lies in  where
where 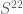 is the (2,2) Schur functor. (Exactly the beautiful and important topic you said you would avoid!) Here are two good ways of thinking about
is the (2,2) Schur functor. (Exactly the beautiful and important topic you said you would avoid!) Here are two good ways of thinking about 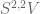 . One is that it is the subspace of
. One is that it is the subspace of 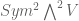 which maps to zero under the natural map to
which maps to zero under the natural map to 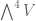 . An equivalent formulation is that
. An equivalent formulation is that 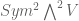 is the space of quadratic polynomials on
is the space of quadratic polynomials on 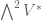 , while
, while  is the quotient space of
is the quotient space of 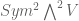 where we identify two quadratic polynomials if they agree on tensors of rank one.
where we identify two quadratic polynomials if they agree on tensors of rank one.
There is a typo in equation (26).
27 March, 2008 at 8:53 am
davidspeyer
A question regarding the definition of torsion free connections by saying that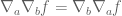 . I read this as saying that, if
. I read this as saying that, if  and
and  are two coordinate vector fields then
are two coordinate vector fields then  . As you say, “any connection on the tangent bundle (which is the case of importance in Riemannian geometry) naturally induces a connection on the cotangent bundle and the bundle of rank (k,l) tensors.” I thought that the connection on (0,0)-forms which was induced in this way was simply
. As you say, “any connection on the tangent bundle (which is the case of importance in Riemannian geometry) naturally induces a connection on the cotangent bundle and the bundle of rank (k,l) tensors.” I thought that the connection on (0,0)-forms which was induced in this way was simply 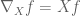 . Nothing else seems consistent with the Liebnitz rule. And, in this case, the requirement above is automatic.
. Nothing else seems consistent with the Liebnitz rule. And, in this case, the requirement above is automatic.
I do understand the definition by equation (15), so I in some sense know what torsion free connections are, but I don’t understand this way of thinking about them.
27 March, 2008 at 12:25 pm
Kestutis Cesnavicius
A small typo: in the comment on the definition of the directional derivative (before “This is a linear functional…”) I believe it should be instead of
instead of 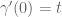 .
.
27 March, 2008 at 12:40 pm
Anonymous
Thanks a lot! Very nice exposition.
In Definition 1, isn’t g a section of V and f a scalar field?
There is a typo in (26), and a zero missing from (27).
27 March, 2008 at 1:09 pm
Terence Tao
Thanks for the corrections! But in definition 1, the Leibnitz rule works both ways (everything here is commutative, as we are not doing noncommutative geometry).
27 March, 2008 at 1:29 pm
Terence Tao
Dear David,
For some reason wordpress classified all your posts as spam; I’ve retrieved them manually, but if you (or anyone else) continues to have problems, please let me know (e.g. by email).
You’re right about Exercise 6; I’ve amended it accordingly. (I may have issues later in the course distinguishing what is true in three-dimensional Riemannian geometry, with what is true in general, since I will be primarily focused on the former; but please continue to nitpick these issues. :-) )
As for the torsion-free business, this is a little subtlety in the abstract placeholder notation (see also the discussion near (10)). Given a frame , the ab coefficient
, the ab coefficient  of the Hessian
of the Hessian  is not just
is not just 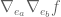 , because the outer derivative
, because the outer derivative  is acting on the vector field
is acting on the vector field  rather than on each component
rather than on each component  separately. Indeed, what one is doing here is first computing the first derivative
separately. Indeed, what one is doing here is first computing the first derivative  , which in coordinates is
, which in coordinates is  and in differential geometry notation is just df, and then taking the covariant derivative
and in differential geometry notation is just df, and then taking the covariant derivative  of that, giving the rank (0,2) tensor whose ab component is equal to
of that, giving the rank (0,2) tensor whose ab component is equal to ![{}[\nabla_{e_a} (df)] e_b = \nabla_{e_a}(\nabla_{e_b} f) + \Gamma_{ab}^c \nabla_{e_c} f](https://s0.wp.com/latex.php?latex=%7B%7D%5B%5Cnabla_%7Be_a%7D+%28df%29%5D+e_b+%3D+%5Cnabla_%7Be_a%7D%28%5Cnabla_%7Be_b%7D+f%29+%2B+%5CGamma_%7Bab%7D%5Ec+%5Cnabla_%7Be_c%7D+f&bg=ffffff&fg=545454&s=0&c=20201002) , where
, where 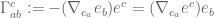 is the Christoffel symbol of the connection relative to the frame. If the vector fields
is the Christoffel symbol of the connection relative to the frame. If the vector fields 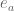 commute with each other (which is for instance the case if they arise from a local coordinate system), the torsion free condition is equivalent to the symmetry
commute with each other (which is for instance the case if they arise from a local coordinate system), the torsion free condition is equivalent to the symmetry  of the Christoffel symbol.
of the Christoffel symbol.
It takes a bit of getting used to, but I find abstract placeholder notation to be by far the quickest way to do Riemannian geometry computations; I have trouble getting the d’s and ‘s and
‘s and  ‘s and *’s sorted out once I have to deal with rank 4 tensors with various idiosyncratic symmetry properties (which happens a lot in Riemannian geometry) :-) .
‘s and *’s sorted out once I have to deal with rank 4 tensors with various idiosyncratic symmetry properties (which happens a lot in Riemannian geometry) :-) .
There is some abstract way to interpret abstract placeholder notation as some sort of morphism from an abstract tensor bundle to a concrete one, but I don’t recall exactly how to set it up properly.
27 March, 2008 at 1:37 pm
dsilvestre
I think on (27) on the first Bianchi identity a “= 0” is missing.
27 March, 2008 at 3:25 pm
anonymous
Dear Prof. Tao,
Missing from the “Online Resources” section of the course webpage is your own “short story” writeup of Perelman’s proof. Perhaps a link would be appropriate?
28 March, 2008 at 2:11 am
Dylan Thurston
Re the definition of torsion-free: the way I understood an expression like was to notice that
was to notice that  is a section of
is a section of  , independent of the connection. Then you can differentiate again, using the connection this time, to get a rank (0,2) tensor, which is required to be symmetric.
, independent of the connection. Then you can differentiate again, using the connection this time, to get a rank (0,2) tensor, which is required to be symmetric.
28 March, 2008 at 2:12 am
Dylan Thurston
Hmm, I don’t know how to get math to come out. Perhaps there should be a link to a reference near the Submit button?
28 March, 2008 at 7:58 am
Anonymous
You have to write “latex ” (without double quotes) just after the first dollar sign of the equation. For example: $ latex R^n$ (remove the first empty space before “latex”) becomes .
.
28 March, 2008 at 8:35 am
Terence Tao
Thanks for the suggestions! I can’t quite seem to modify the CSS to change the comment box directly, but I put some text about LaTeX just below and to the left of it.
28 March, 2008 at 9:26 am
285G, Lecture 1: Flows on Riemannian manifolds « What’s new
[…] Exercise 1. Show that (12) is consistent with the antisymmetry properties of the Riemann tensor, and with the Bianchi identities, as presented in the previous lecture. […]
28 March, 2008 at 3:10 pm
nobody
Dear Professor Tao,
What exactly makes a connection as in definition 1 “affine”? I was under the impression that an affine connection was one on the tangent bundle.
Also, in remark 5, what is the ambiguity in the O(t^3) characterization of torsion-freeness that leads you to say that this is only “roughly speaking”? It seems to me that this would be a perfectly valid alternative definition.
By the way, if my understanding is correct, the curvature does not measure the monodromy of parallel transport; it only does so infinitesimally. In particular, it is insensitive to the topology (in particular, the fundamental group) of the manifold.
28 March, 2008 at 3:52 pm
Terence Tao
Dear nobody,
Hmm, you’re right. I was confusing “affine connection” with “linear connection”. (Somewhat counterintuitively, the latter is a special case of the former, rather than the other way around.)
One can make remark 5 more precise but one has to make clearer what it means to transport an edge of length t “by parallel transport” by a distance t up to accuracy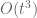 . This can be done, but requires a small amount of care.
. This can be done, but requires a small amount of care.
I’ve amended the remark on monodromy to emphasise it is only measuring _infinitesimal_ monodromy.
28 March, 2008 at 11:13 pm
Michael Kinyon
In the sentence preceding Definition 1, I think “notation” should be “notion”. (When reading it, I flashed on the old joke about differential geometry being the study of properties which are invariant under change of notation.)
29 March, 2008 at 2:30 am
Terence Tao
Thanks for the correction!
31 March, 2008 at 6:41 am
Arbieto
Dear Prof. Tao
I´m quite impressive for your exposition on geometric flows.
Oh, and I think that there is a typo when you talk about symmetric powers.
1 April, 2008 at 9:19 am
285G, Lecture 2: The Ricci flow approach to the Poincaré conjecture « What’s new
[…] structure, and with two manifolds considered equivalent if they are homeomorphic. As mentioned in Lecture 0, in three dimensions it is not difficult to move from the topological category back to the smooth […]
21 April, 2008 at 8:03 pm
285G, Lecture 7: Rescaling of Ricci flows and kappa-noncollapsing « What’s new
[…] one is the minimal scalar curvature . One can check (cf. the dimensional analysis at the end of Lecture 0) that scalar curvature has dimension -2 and is thus subcritical. The quantity , that measures the […]
24 April, 2008 at 5:36 pm
285A, Lecture 8: Ricci flow as a gradient flow, log-Sobolev inequalities, and Perelman entropy « What’s new
[…] prove the second identity, differentiate (30) and use the second Bianchi identity (Exercise 7 from Lecture 0).) Use the maximum principle to then conclude that the only compact gradient steady solitons are […]
16 May, 2008 at 4:14 pm
285G, Lecture 12: High curvature regions of Ricci flow and κ-solutions « What’s new
[…] RIemann curvature is equivalent to that of non-negative sectional curvature; see the discussion in Lecture 0. In any dimension, the conditions of non-negative bounded Riemann curvature imply that R and are […]
19 May, 2008 at 2:17 pm
285G, Lecture 13: Li-Yau-Hamilton Harnack inequalities and κ-solutions « What’s new
[…] identities make the Riemann, Ricci, and scalar curvatures are all essentially equivalent (see Lecture 0); in particular one has the […]
21 May, 2008 at 2:50 pm
Weiqi Gao
The definition of![{}[\nabla_X, \nabla_Y]](https://s0.wp.com/latex.php?latex=%7B%7D%5B%5Cnabla_X%2C+%5Cnabla_Y%5D&bg=ffffff&fg=545454&s=0&c=20201002) between formulas (3) and (4) contains a formula typo. Shouldn’t it be
between formulas (3) and (4) contains a formula typo. Shouldn’t it be 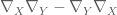 ?
?
21 May, 2008 at 5:32 pm
Terence Tao
Dear Weiqi: Thanks for the correction!
1 June, 2008 at 3:02 pm
285G, Lecture 16: Classification of asymptotic gradient shrinking solitons « What’s new
[…] the Ricci tensor is conformal: . Comparing this with the Bianchi identity (equation (28) from Lecture 0) we conclude that , and thus . Thus M has constant sectional curvature and is therefore a round […]
28 June, 2008 at 3:07 pm
The trouble with commuting II « The Pablog
[…] Physics. An excellent review of the basic structures used in Riemannian Geometry may be found on here on Terry Tao’s blog. Possibly related posts: (automatically generated)Living With The […]
9 July, 2008 at 10:32 am
Mohammad
Dear Prof Tao,
I think there is a typo in the schematic representation of Laplacian ( number 1 above the Remark 8 ), the second term should be g^-2*(dg)*dw .
10 July, 2008 at 9:41 am
Terence Tao
Dear Mohammad: thanks for the correction!
10 July, 2008 at 2:24 pm
JC
Hi, now the formula pointed out by Mohammed doesn’t parse.
10 July, 2008 at 5:28 pm
Terence Tao
Oops! Fixed now.
11 July, 2008 at 4:32 am
BD
The formula pointed out by Mohammad has been corrected wrongly!
11 July, 2008 at 9:11 am
Terence Tao
Ack! Glad to know that people are paying attention, at least.
28 September, 2008 at 12:18 am
ahmad
too high qualified ,u r talended thank u
29 September, 2008 at 8:49 am
What is a gauge? « What’s new
[…] a manner as possible; the precise definition is a little technical (see e.g. my lecture notes for a brief description). Suppose for instance one starts at some location x on the equator of […]
19 April, 2009 at 12:18 am
Paul Cernea
Dear Professor Tao,
First, thanks for posting this lecture series (and in fact the whole blog)! It’s truly illuminating for students like me who are trying to understand Ricci Flow.
Second, below Definition 3 you give a geometric interpretation of the different kinds of positive curvatures. I think I may have found a typo, but I’m not sure. You write that positive sectional curvature means that all infinitesimally geodesic surfaces have positive mean curvature. I know the analogous statement holds for positive Gaussian curvature. Is it also true for mean curvature?
Best regards,
Paul
19 April, 2009 at 1:53 pm
Terence Tao
Ah yes, you’re right, I meant positive Gaussian curvature here, thanks.
18 July, 2010 at 12:55 pm
Problemy milenijne matematyki – zaczyn do dyskusji « Jaronwoj Blog Warszawa Polska
[…] https://terrytao.wordpress.com/2008/03/26/285g-lecture-0-riemannian-manifolds-and-curvature/ […]
16 December, 2011 at 10:14 am
254B, Notes 3: Quasirandom groups, expansion, and Selberg’s 3/16 theorem « What’s new
[…] geometry, as well as the functional analysis of Sobolev spaces and distributions. See for instance this blog post for a very brief introduction to Riemannian geometry, and these two previous posts for an […]
29 December, 2012 at 1:05 pm
A mathematical formalisation of dimensional analysis « What’s new
[…] One can also assign dimensions to higher rank tensors, such as matrices, -vectors, or -forms; the notation here becomes rather complicated, but is perhaps best described using abstract index notation. The dimensional consistency of equations involving such tensors then becomes the requirement in abstract index notation that the subscripts and superscripts on the left-hand side of a tensor equation must match those on the right-hand side, after “canceling” any index that appears as both a subscript and a superscript on one side. (Abstract index notation is discussed further in this previous blog post.) […]
1 March, 2013 at 9:09 pm
anonymousCoward
Could you please clarify Exercise 2. Is the expectation to show uniqueness or to show that the difference of two covariant derivatives has the desired transformation property between overlapping charts?
1 March, 2013 at 9:41 pm
Terence Tao
The question asks for both existence and uniqueness of the tensor .
.
11 April, 2013 at 2:38 am
Conjectura de Poincaré explicada por Terry Tao | Adsu's Blog
[…] en 20 posts de la demostración de la conjetura de Poincaré hecha por Perelman. Enlazo aquí su Lecture 0 que nos puede servir tanto como introducción de los conceptos básicos de la geometría […]
25 May, 2015 at 1:58 pm
anon
Hi, huge thanks for this great crash course. A few typos:
1) Before Definition 1: an connection -> a connection
2) Before (10): Gamma(M) -> Gamma(TM)
3) After (14): ref to Clairaut’s theorem should refer to http://en.wikipedia.org/wiki/Symmetry_of_second_derivatives
4) (26) : exchange Del_alpha and Del_delta in the second summand
5) Some lines above Exercice 9: Change (see Exercice 8 below) to (see Exercice 9 below)
[Corrected, thanks – T.]
19 January, 2016 at 1:43 pm
Anonymous
what is the formula (26)? “formula does not parse”
[Not sure why this formula was not parsing before, but it seems to work now -T.]
20 January, 2016 at 11:53 pm
Anonymous
Formula (26) is just formula (24”) with omega replaced by nabla f. You can see the LaTeX for (26) by hovering your mouse over it, but beware that it has a typo (indices on the LHS should be “alpha beta delta – beta alpha delta”) although that shouldn’t cause the parse error.
8 October, 2017 at 12:10 am
Maths student
I’ve thought about whether in the informal description of tangent vectors, already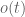 would be enough; I mean, this would already determine the derivative at
would be enough; I mean, this would already determine the derivative at  , right?
, right?
[Yes, though as long as the manifold is smooth, there is no real distinction between the two error rates (and for rough manifolds, defining geometric concepts such as curvature can become quite problematic if not done carefully -T.]
25 October, 2017 at 7:04 pm
qinyu95
Reblogged this on qinyugong.
8 August, 2023 at 2:37 pm
[讲义]黎曼流形入门 – 王俊凯@Physics
[…] 285G, Lecture 0: Riemannian manifolds and curvature […]