On Thursday, UCLA hosted a “Fields Medalist Symposium“, in which four of the six University of California-affiliated Fields Medalists (Vaughan Jones (1990), Efim Zelmanov (1994), Richard Borcherds (1998), and myself (2006)) gave talks of varying levels of technical sophistication. (The other two are Michael Freedman (1986) and Steven Smale (1966), who could not attend.) The slides for my own talks are available here.
The talks were in order of the year in which the medal was awarded: we began with Vaughan, who spoke on “Flatland: a great place to do algebra”, then Efim, who spoke on “Pro-finite groups”, Richard, who spoke on “What is a quantum field theory?”, and myself, on “Nilsequences and the primes.” The audience was quite mixed, ranging from mathematics faculty to undergraduates to alumni to curiosity seekers, and I severely doubt that every audience member understood every talk, but there was something for everyone, and for me personally it was fantastic to see some perspectives from first-class mathematicians on some wonderful areas of mathematics outside of my own fields of expertise.
Disclaimer: the summaries below are reconstructed from my notes and from some hasty web research; I don’t vouch for 100% accuracy of the mathematical content, and would welcome corrections.
Vaughan Jones – “Flatland: a great place to do algebra”
Vaughan gave a very accessible and engaging public lecture, that managed the rare feat of being both non-technical, and yet packing in a surprising amount of meaty mathematics. He began by noting how the Cartesian co-ordinate system of Descartes had demystified the notion of dimension, reducing the two-dimensional plane to collections of pairs of numbers, the three-dimensional space to triplets of numbers, and so forth. Of course, even so, the notion of the “fourth dimension” and beyond still retains a certain almost magical appeal, and Vaughan illustrated this by discussing the classic book “Flatland” by Edwin Abbott, which mostly revolves around a society of two-dimensional intelligent beings, and the difficulty they have with even conceiving of the third dimension. (As an amusing side note, Vaughan quoted a reviewer of that book from that era approving of Abbott’s higher-dimensional speculations as likely to be more significant than those of his contemporary Hamilton, who had just invented the quaternionic number system.)
Vaughan then talked about his own mathematical journey through dimensions, starting out in the infinite-dimensional theory of von Neumann algebras (in particular, in his celebrated paper developing an index theory for subfactors of von Neumann algebras), and then descending to three dimensions (through his achievements in knot theory) and more recently to two dimensions (through planar algebras). To describe the connections between all these topics, Vaughan first recalled how knots can be obtained from braids by tying the ends together; or equivalently, how braids can be viewed as “knots-with-boundary”. This brings group theory into the picture, because braids form a group. He then talked about Louis Kaufmann’s fundamental insight that braids (which can be viewed as a three-dimensional object) can be converted by a simple operation to a planar object (an element of the Temperley-Lieb algebra, which had also appeared in Vaughan’s paper on index theory). This led naturally to the more general notion of a planar algebra, which can very vaguely be viewed as a two-dimensional version of the more “linear” model of algebra (a sequence of one-input and one-output functions composed together), in which inputs and outputs are connected together by a planar tangle (a collection of non-crossing curves and loops). Other interesting examples of planar algebras included knots with boundary (as proposed by Conway) and tensors (as proposed by Penrose). He then noted how crucial the planarity was in order to obtain a rich algebraic structure; apparently, much of this interesting structure collapses if one allows the components in a tangle to cross each other. (As an analogy, he mentioned how much more rigid and easy a game of sudoku would be if one worked in and required all coordinate 2-planes (from all six families) to be labeled with some permutation of {1,…,9}, as opposed to just three of the families (the rows, the columns, and the squares, which are also all connected planar objects).)
To close, Vaughan mentioned how vertex algebra structures also arise naturally in the quantum theory of lattices, and in particular (as proposed by Freedman and others) could be useful in designing quantum computers. He then noted that the theory of the braid group (including of course the Jones polynomial) could also be viewed as the theory of dynamics of non-colliding points in the plane (by viewing time as a third dimension); quantising this, one then expects braid groups to play a role in the quantum Hall effect (and its fractional generalisation) that manifests itself at incredibly low temperatures, although despite many breakthroughs in the area, there has not yet been a physical model proposed that would truly be governed by a non-abelian braid group.
Efim Zelmanov – “Pro-finite groups”
Efim gave a much more technical, but also very beautiful, talk on some cutting edge research in group theory, revolving around the extent to which a group can be understood from a prescribed set of relations. One seeks to study infinite groups here, but Efim clearly distinguished between the “hopelessly infinite” groups, and the groups which are at least residually finite – groups which have enough finite models that one can distinguish points. For instance, the integers are residually finite because given any two distinct integers x, y, one can find a homomorphism
into a finite group which sends x and y to different values. One can then view a residually finite group as a subgroup of an infinite product of finite groups. If this subgroup is topologically complete, we say the group is pro-finite; the p-adics are a good example, as are the Galois groups
. One can localise these notions to a fixed (rational) prime p (replacing the notion of “finite group” with “finite p-group“), giving rise to the stricter notions of residually p-finite and pro-p-finite groups. The p-adics are again a good example of a pro-p-finite group. A little less obviously, the free (non-abelian) group
on m generators is residually p-finite for every p, and has a pro-p-finite completion
. An important “linear” example of a pro-p-finite group comes from the congruence subgroup
of
matrices over a commutative complete Noetherian ring
which are trivial when quotiented by a maximal ideal M whose quotient field is a characteristic p finite field; more generally, we say that a pro-p-finite group is linear if it is isomorphic to a subgroup of such a congruence subgroup.
The pro-p-completed free group F on m generators is universal, in the sense that every pro-p-group G with m generators can be realised as a quotient of F by the (completed) ideal generated by a collection of relations R. In principle, the relations R describe the group G completely (up to isomorphism, of course), but in practice, even such basic questions as whether G is finite or infinite can be difficult to discern just from the relations R. A fundamental result in this area is the Golod-Shafarevich theorem, which asserts that if there are sufficiently few relations (more precisely, ) and if one makes the technical hypothesis that the relations lie in the p-commutator
, then the group is infinite. Groups which obey these hypotheses are known as GS-groups. For instance, many Galois groups turn out to be GS-groups and thus infinite, which is an important fact to know in algebraic number theory.
Another important class of GS groups arise as the fundamental groups of compact hyperbolic 3-manifolds; Lubotzky showed that these are GS groups for all sufficiently large p. An important conjecture in this area is the virtual positive Betti number conjecture (due to Thurston and Waldhausen), which asserts that such groups have a large abelian subquotient, or more precisely there exists a finite index subgroup H which has a surjective image onto
. This conjecture is backed up by some impressive numerical evidence. Lubotzky and Sarnak observed that if this conjecture was true, it would imply the weaker conjecture that
does not have property
; this is now known as the Lubotzky-Sarnak conjecture. Recently, Lackenby showed a converse implication (deducing the Betti number conjecture from the Lubotzky-Sarnak conjecture) in the case of arithmetic groups. Efim and Lubotzky then conjectured that the LS conjecture in fact extends to all GS groups, but this was disproven by an explicit counterexample last year by Ershov. So it seems that there is more to these fundamental groups than just the GS property, at least if one believes these conjectures.
Efim then turned from low-dimensional topology to number theory, and in particular to questions relating to the Fontaine-Mazur conjecture, which asserts that Galois groups are so “nonlinear” that their image in any
can have only finite image. A weaker version of this conjecture asserts that such Galois groups are not linear in the sense mentioned earlier. These Galois groups are GS groups, and Efim showed that GS groups contain a copy of the pro-p-finite group F, and so to prove this weaker conjecture it would suffice to show that F is not linear, i.e. that F does not embed injectively into
for any n and
. This was shown by Zubkov when n=2, and very recently Efim verified the conjecture when n is arbitrary and p is sufficiently large depending on n. The question reduces to one of locating universal identities for generic
matrices over the p-adics (since the free group F, by definition, will not obey such identities). To prove this Efim had to generalise the problem to a representation theoretic version and “induct on representations”; I unfortunately didn’t understand this bit too well. As a consequence Efim showed that such universal identities exist, but his argument was non-constructive, so no explicit such identity is known.
Efim then closed by talking a little more about universal identities; he mentioned the Specht conjecture (proven by Kemer) that over a field of characteristic 0, there are only finitely many universal identities which generate all the others in a syntactical sense (i.e. by the laws of algebra). He then made the interesting remark that there appears to be essentially one and only one technique known to establish finiteness theorems (such as this one) in algebra, namely to appeal to Hilbert’s basis theorem (which asserts that every ideal in a finitely generated commutative ring is itself finitely generated).
Richard Borcherds – “What is a quantum field theory?”
Richard is best known for his work in lattices and group theory, most notably in explaining the monstrous moonshine phenomenon, but in recent years he has moved to a completely different area of mathematics, namely mathematical quantum field theory (QFT), which Richard did a very admirable job of explaining. He began by contrasting the very different perspectives of mathematicians and physicists to the subject; from the mathematical side of things, he mentioned the various axiomatic formulations proposed for QFT (Wightman axioms, Haag-Kastler axioms, Ostewalder-Schrader axioms, etc.), but then mentioned the main difficulty with these formulations, namely that none of the major interacting four-dimensional spacetime QFTs (QED, QCD, standard model, etc.) are known to obey any of these axioms. (The free QFTs obey the axioms, as well as many two-dimensional and a few three-dimensional ones.) On the physical side, the emphasis is more on computing the Green’s function for a QFT, which formally can be expressed as a Feynman path integral, which in turn is formally expandable as an infinite sum (essentially a Dyson series) over Feynman diagrams of various finite-dimensional integrals; these sums are often horribly divergent, but nevertheless by means of various tricks of varying levels of mathematical rigour, physicists have been able to compute at least the first few terms of these sums and get some predictions which are in extraordinary agreement with experimental data. Most of Richard’s talk was on explaining how the mathematical and physical viewpoints could (hopefully) be reconciled.
Richard gave us a very interesting and useful “complexity hierarchy” to view the various spaces in both classical and quantum field theory, using things like the symmetric algebra construction to go from one level to the next (thus one can view spaces in level n+1 as consisting of some sort of “polynomials” of objects in a level n space). According to Richard, one of the main reasons why QFT is conceptually difficult is that it routinely uses spaces which are very high up in the hierarchy. For example, in a classical field theory (CFT), ignoring all analytic questions of convergence, differentiability, integrability, etc.,
- “Level 0” spaces are finite-dimensional spaces such as the spacetime M, the gauge group G, the principal vector bundle B over M, and so forth. (For instance, in a scalar field theory, G is the real line, and B is just
.) Classical fields
are then just sections of these bundles; for instance, a scalar field is just a map
. The jet bundles of B also qualify as Level 0 spaces.
- “Level 1” spaces include things like the space of differential operators on M (or on the bundle B), which can be viewed as polynomials over the “Level 0” vector fields
. For instance, the d’Alembertian
would belong to this Level 1 space. A little more generally, the Poisson algebra of a jet bundle is a Level 1 space.
- “Level 2” spaces include the space of polynomial combinations of objects from Level 1 spaces applied to a classical field
. In particular the space
of Lagrangian densities, of which
is a typical example, is a Level 2 object. This is the level where standard explanations of classical field theory usually stop; the theory asserts that classical fields must be critical points for the associated action
, and that is an adequate description of the theory. But one can continue onward:
- “Level 3” spaces include the Poisson algebra generated by
, which contains such objects as the Poisson bracket
between two actions. This algebra is implicit in things such as Noether’s theorem, but is usually not discussed explicitly. Using the Poisson bracket structure, elements of this Level 3 space can be viewed as “vector fields” or “flows” on the space of all fields in the classical field theory; in particular, infinitesimal symmetries live in a Level 3 space.
- “Level 4” spaces include the universal enveloping algebra of the previously mentioned Poisson algebra (which is of course a Lie algebra). This is where “differential operators” on the space of all fields will live. I think also that canonical transformations (such as those given by non-infinitesimal symmetries, e.g. spatial translation by a non-zero distance) are also supposed to (formally) lie in a Level 4 space, though I am a bit uncertain on this point.
So while CFTs mostly top out at Level 2, QFTs seem to really require all levels up to Level 4:
- “Level 0” spaces of a QFT are much the same as those of the associated CFT: the spacetime, the bundle, etc. The quantum fields
are no longer sections of the bundle, though, but should be interpreted for each x as (nastily singular and unbounded) operators on some abstract Hilbert space (it seems to be unprofitable to try to make this space concrete until much later in the theory). (Incidentally, these quantum fields are not the wave function
that one is used to from the Schrödinger formulation of non-relativistic quantum mechanics, but instead represent the (spacetime) position operators from the Heisenberg formulation.)
- “Level 1” spaces again include the space of differential operators, but now acting on quantum fields rather than classical fields. (There is of course the usual problem that these operators might be unbounded and thus only be densely defined on the Hilbert space of interest, but there are standard ways to deal with these difficulties.)
- “Level 2” spaces again include the space
of all Lagrangians, are polynomials that convert a quantum field
to another (formally) operator-valued function of space time.
- “Level 3” spaces include the space of all Feynman path integrals, e.g.
. In particular they include Green’s functions.
- “Level 4” spaces include the space of generalised Wightman distributions, which include things like
where
is the vacuum state and
are various bump functions in spacetime, but also include more general objects in which the
factors are replaced by any other time-ordered operators, such as those coming from the Level 3 space. (I admit I didn’t understand this point very well.) Apparently, the space of all renormalisations is also a Level 4 space.
Richard then talked about the various attempts to build a QFT starting from the Lagrangian as the foundational object. He mentioned Dirac’s philosophy of building the Lie algebra structures first, and only worrying about exactly what the Hilbert space H was at a very late stage of the theory; indeed, trying to apply standard “prequantisation” methods such as proposing as the Hilbert space seemed to run into fundamental difficulties (e.g. the action of the center was wrong). There was some fix to this involving the choice of a “polarisation”, but this seemed somewhat ad hoc and didn’t seem to work in all cases (I didn’t follow this bit well). [Incidentally, Richard made a cute observation, which was that the theory becomes a little cleaner notationally when Hilbert spaces were not viewed as complex vector spaces, but rather as complex bimodules, with the complex numbers acting in the usual linear manner on the left but in an antilinear manner on the right,
. More generally, operators should act on vectors on the left in the usual manner but on the right by the adjoint operator. This ends up reconciling the “mathematical” and “physical” notation in the subject quite nicely.]
A more promising approach was to start by computing the Wightman distributions (which are slight variants of the Green’s function, the differences being technical and having to do with the time-ordering of the spacetime points
; the two can be related to each other via analytic continuation), and use that to construct the Hilbert space, or at least the portion of the Hilbert space generated from the vacuum state, via the GNS construction. (There are problems due to
being singular, but this can basically be dealt with by the theory of distributions.) This approach fits well with the Wightman axiom formulation of QFT mentioned earlier; unfortunately, it is not known how to make all the relevant series converge in order to verify these axioms for any of the physically relevant QFTs. However, one can often proceed perturbatively, which can be formalised by replacing the underlying field
(a field in the mathematical sense, not the physical one!) with the field of formal power series
, where
denotes the (dimensionless) coupling constants of the theory (e.g. the fine structure constant, which basically represents the charge of the electron) and which show up in the interaction (i.e. non-quadratic) terms of the Lagrangian. There are some significant mathematical problems in working with this perturbative field (in particular, the notion of positivity, or of completeness, has to be carefully redefined) but these are reasonably tractable issues. But even when working perturbatively, the individual terms in the Dyson series used to compute path integrals are usually still divergent. To extract meaningful values for these expressions, physicists employ the twin devices of regularisation and renormalisation. Regularisation introduces a smoothing parameter s to help the integral converge, sending
at the end of the day; one can either use s to modify the ambient dimension of the spacetime (which is somewhat dubious mathematically, since spacetime is only supposed to have a nonnegative integer number of dimensions rather than complex!), or to strengthen the dissipative and dispersive nature of the Laplacian by raising it to another power (here one is on firmer ground mathematically, thanks to the well established theory of pseudo-differential operators). However, even when one regularises, the terms still blow up in the limit
if the parameters
are kept fixed. However, one can renormalise away this issue by redefining
to be a certain meromorphic function of s, in such a way that a finite limit can now be extracted. This means that
goes to infinity as s goes to zero; for instance in QED, this is the assertion that the electron actually has an infinite “bare” charge but a finite “effective” charge. There can be multiple choices of renormalisation, but there are transformations which convert one to the other (I didn’t understand this point well). There is also some way to view renormalisations as some sort of coproduct-preserving homomorphism from the Level 3 space of all Green’s function-type objects to itself, but I was a little lost by this point.
Richard closed by giving an “executive summary” of QFT as being the unitary representation theory of a certain “Level 4” space (some sort of Lie algebra, I think) which incorporated the Lagrangian, the Poincaré group, and the complex structure (but quotiented somehow by the constraint of locality); all of these ingredients are basically mandated by the Wightman axioms.
Terence Tao – “Nilsequences and the primes”
Here I gave a more detailed presentation of the material I had discussed in my first Simons lecture, and focussing a bit more on the role of nilflows in characterising the “structure” or “conspiracies” which seem to control the additive behaviour of primes, as arising with my work with Ben Green, and also on the very recent connections between this work and Ratner’s theorem. My slides are available here.

16 comments
Comments feed for this article
27 April, 2007 at 11:53 am
Anon
Is monstrous moonshine really a completely different area? I was under the impression that vertex operators, infinite dimensional Grassmannians, and generalized Kac-Moody algebras arise naturally in conformal field theories, which are a baby version of QFT’s proper. Indeed, as far as I am aware Borcherd’s proof crucially relied on the no-ghost theorem from perturbative string theory.
27 April, 2007 at 12:06 pm
Terence Tao
Well, it’s outside my field, so I can’t really say, though Richard did tell me yesterday that he considers himself as having moved away from moonshine quite a bit, but perhaps this is only in regard to the focus of study, rather than the mathematical technology employed. He did list vertex algebras and Verma modules of affine Kac-Moody algebras as examples of “Level 2” objects, though, in his talk. (Verma modules of plain old Lie algebras are merely “Level 1” objects.)
27 April, 2007 at 6:51 pm
Greg Kuperberg
The symposium sounds very interesting, but it reminds of a quip that I made at a workshop that I attended not long ago. The workshop had an informal lunch buffet — I’m not sure that they even bothered with tablecloths — and a group of us had picked a particular table. I think that one Fields Medalist at the workshop (who shall remain nameless) was to eat with us. But he lost track of that and sat down with the other Fields Medalist at the workshop (who shall also remain nameless) at another table. So I said to the rest of the lunch party, “If it were only one Fields Medalist, we could still ask him to come sit with us. But since it’s two Fields Medalists, I think that we’re outvoted.” :-)
Anyway, to address the math question, yes, I believe that vertex operator algebras are intended as a axiomatization of a simplified part of conformal field theory. One of the simplifications is to restrict to CFT on a sphere with marked points, instead of surfaces with higher genus. Monstrous moonshine is an example CFT which is constructed with a certain amount of symmetry (that of the Leech lattice) but is revealed to have more symmetry (that of the monster group). It’s not my area either, but I think that this is a fair summary of what I have been told.
However, there is a great variety of quantum field theories in the world, so that you can easily move far away from any one set of examples and still do quantum field theory.
29 April, 2007 at 12:57 pm
Not Even Wrong » Blog Archive » Various Events and Other News
[…] the Fields Medalist blogging front, there’s a report from Terry Tao about a symposium at UCLA where he and three other Fields medalists gave talks. He gives a detailed […]
1 May, 2007 at 3:19 pm
Yi-Zhi Huang
Vertex operator algebras are the algebras of meromorphic
quantum fields on the sphere. Rartional conformal field
theories on the sphere and on the torus have now been
constructed mathematically using the representation theory
of vertex operator algebras. The higher-genus case
might be a little tedious but no fundamental difficulties
are expected. Indeed, in this construction, the Hilbert space
structure is the last step. Actually one can introduce the
Hilbert space structure using a suitable inner product
from the beginning but it is not very useful.
What we need is a nice dense subspace of the Hilbert
space constructed from representations of the vertex operartor
algebra such that correlation functions on Riemann surfaces
associated to elements of this dense subspace
can be constructed. Then in the last step, one can use these
correlation functions to give a topological completion
(not the inner product completion) of
the dense subspace and show that this completion is the
same as the inner product completion.
Now it is clear why the direct use of the Hilbert space might be
difficult: We can look at the construction of the Hilbert
space using correlation functions. These correlation functions
involve higher genus Riemann surface structure, but from the
Hilbert space structure obtained from
the inner product completion, we do not see anything
about Riemann surfaces.
1 May, 2007 at 5:40 pm
stevenm
Thanks for taking the time to provide summaries of these interesting talks. In Jones’ talk you mention he discusses the braid group and the Jones polynomial within the context of describing the dynamics of non-colliding points in the plane. I am wondering if he was referring to ‘vicious walkers’, which are Brownian motions or random walkers not allowed to intersect or which can annihilate when they meet. The probability densities for these types of random walks (for N particles) can be related to the partition function of a Chern-Simons theory on the 3-manifold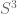 with gauge group U(N). As regards the Jones polynomial and QFT, a beautiful and quite famous result that should perhaps be mentioned here is that of Witten who demonstrated that the Jones polynomial has a
with gauge group U(N). As regards the Jones polynomial and QFT, a beautiful and quite famous result that should perhaps be mentioned here is that of Witten who demonstrated that the Jones polynomial has a
representation in terms of a topological quantum field theory, namely an non-abelian SU(2) Chern-Simons theory on a 3-manifold. In a sense, this result would also seem to be bridge between the talks of Jones and that of Borcherds on QFT. The problem mathematicians have with this construction of the Jones is the usual lack of a rigorous definition of the Feynman path integral measure, although for once the path integral here can actually be performed exactly.
I always find it particularly fascinating when fields that at first seem unrelated turn out to have these tantalizing connections: the Jones connects with von Neumann algebras, statistical mechanics, braids etc. as you mentioned, but also with 3-dimensional topological quantum field theory. In molecular biology the Jones polynomial–and its generalisations like the HOMFLY polynomial, derivable from the SU(N) Chern-Simons–are also a potentially useful and powerful tool in classifying and identifying knotted states and topological properties of dna, polymers and enzymes; essentially ‘biological strings’. But an SU(N) Chern-Simons theory can also be related to topological string theory in the large N limit. A lot of fascinating things and connections going on here. Incidently, did Borcherd mention anything about the hard problems of actually defining QFTs on 4-manifolds, specifically the Yang-Mills gauge theory, which of course is a Clay problem?
3 May, 2007 at 9:37 am
Terence Tao
Dear Stevenm,
Thanks for the interesting comments. Vaughan didn’t mention any sort of random walks in his talk, but given that these things already show up in classical stochastic field theories I am not surprised that some version of them also shows up in QFTs. As for the 4-dim QFTs, the sense I got from Richard was that the algebraic issues (working in the perturbative regime of formal power series) are reasonably well understood and on a fairly solid foundation, but all the analytic issues remain extremely difficult. (As an analogy, one can easily construct “global” “solutions” to the Navier-Stokes equation from analytic initial data by a formal power series expansion (e.g. using Cauchy-Kowaleski), but without any convergence result on such formal power series, this formal power series sheds no light on the global regularity problem.)
5 May, 2007 at 1:20 pm
Scott Carnahan
I’m not an expert on renormalization, but my impression was that there is a space of Lagrangians, a space of renormalization prescriptions (basically perturbative Feynman path integral measures), and a way to combine a Lagrangian with a renormalization prescription to get a “quantum field theory”, which is a family of Green’s functions or generalized Wightman distributions. The group of renormalizations is some infinite dimensional nonabelian nilpotent group that acts on both spaces (changing coupling constants, counterterms, etc), in a way that the resulting quantum field theory is fixed. Finite dimensional orbits of this action on Lagrangians are called renormalizable.
I think Witten proposed the mass gap problem as a Clay prize problem in part because of its very nonperturbative nature. He has mentioned in some articles that there is both theoretical and computational evidence that the mass gap is exponentially damped as coupling constants are taken to zero. Since perturbative expanions are basically calculating in a formal neighborhood of zero, it sounds like they would be quite useless for this problem.
10 June, 2007 at 1:53 pm
Infinite Reflections » Blog Archive » Terry Tao’s Career Advice and Prime Number Colloqium …
[…] A more technical talk is his Nilsequences and the primes – (The lack of) hidden patterns in the prime numbers [Fields Medalists Symposium- April 26, 2007 with Ben Green (Cambridge)] – [via his blog here […]
18 June, 2007 at 11:27 pm
Machine Learning (Theory) » How is Compressed Sensing going to change Machine Learning ?
[…] Tao, the recent Fields medalist, does a very nice job at explaining the framework here. He goes further in the theory description […]
27 June, 2009 at 7:02 pm
Anonymous
Dear Prof. Tao,
I am wondering who decides to give Fields Medal to whom?
is there a fix committe, does it change each year?
if someone is working on statistics, do you think that it is possible to get Fields medals?
thanks
15 September, 2010 at 12:39 pm
Robert
Nice article as always (I myself am interested in the mathematics of quantum field theory).
Small typographical correction: it’s “d’Alembertian” not “d’Lambertian”. Indeed, d’ followed by a consonant makes no sense. [Corrected, thanks – T.]
10 June, 2013 at 4:30 pm
galoisrepresentations
Dear Terry, In your discussion of the Zelmanov’s talk, it’s probably important to define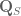 : it is the maximal Galois extension of the rationals which is unramified away from a finite set of primes
: it is the maximal Galois extension of the rationals which is unramified away from a finite set of primes  . Moreover, one only expects that the image of this group in a p-adic linear group will have finite image when the set
. Moreover, one only expects that the image of this group in a p-adic linear group will have finite image when the set  does not contain the prime
does not contain the prime  . The “usual” Fontaine-Mazur conjecture allows
. The “usual” Fontaine-Mazur conjecture allows  to be in
to be in  , in which case there are many interesting infinite image linear representations (for example, coming from the Tate modules of Elliptic curves, or from the cyclotomic character on the
, in which case there are many interesting infinite image linear representations (for example, coming from the Tate modules of Elliptic curves, or from the cyclotomic character on the 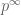 roots of unity).
roots of unity).
29 July, 2019 at 2:00 pm
Anonymous
Wow! The works and awards of Prof. T. Tao are extraordinary!
Link: https://en.wikipedia.org/wiki/Terence_Tao
30 July, 2019 at 9:01 pm
Anonymous
The journey is over, and this is a final goodbye.
22 August, 2019 at 3:26 pm
Anonymous
Oops! The journey is not over… And my math work is not done. And I am still learning from Prof. T. Tao.