The Skolem-Mahler-Lech theorem in algebraic number theory is a significant generalisation of the obvious statement that a polynomial either has finitely many zeroes (in particular, the set of zeroes is bounded), or it vanishes identically. It appeals to me (despite not really being within my areas of expertise) because it is one of the simplest (non-artificial) results I know of which (currently) comes with an ineffective bound – a bound which is provably finite, but which cannot be computed! It appears that to obtain an effective result, one may need a rather different proof. (I thank Kousha Etessami and Tom Lenagan for drawing this problem to my attention.)
Ineffective bounds seem to arise particularly often in number theory. I am aware of at least three ways in which they come in:
- By using methods from soft (infinitary) analysis.
- By using the fact that any finite set in a metric space is bounded (i.e. is contained in a ball of finite radius centred at a designated origin).
- By using the fact that any set of finite diameter in a metric space is bounded.
Regarding #1, there are often ways to make these arguments quantitative and effective, as discussed in my previous post. But #2 and #3 seem to be irreducibly ineffective: if you know that a set A has finite cardinality or finite diameter, you know it has finite distance to the origin, but an upper bound on the cardinality or diameter does not translate to an effective bound on the radius of the ball centred at the origin needed to contain the set. [In the spirit of the preceding post, one can conclude an effective “meta-bound” on such a set, establishing a large annulus in which the set has no presence, but this is not particularly satisfactory.] The problem with the Skolem-Mahler-Lech theorem is that all the known proofs use #2 at some point.
So, what is the Skolem-Mahler-Lech theorem? There are many ways to phrase it, but let us use the formulation using linear recurrence sequences, and in particular restrict attention to integer linear recurrence sequences for simplicity (which was the scope of the original result of Skolem; Mahler and Lech handled algebraic numbers and elements of fields of characteristic zero respectively. The situation in positive characteristic is more subtle, as this recent paper of Derksen shows). By definition, an integer linear recurrence sequence is a sequence of integers which obeys a linear recurrence relation
for some integer (the degree of the linear recurrence sequence), some integer coefficients
with
non-zero, and all
. This data, together with the first d values
of the sequence, clearly determine the entire sequence. The most famous example of a linear recurrence sequence is of course the Fibonacci sequence
given by
;
.
It is also a nice exercise to show that any polynomial sequence (e.g. the squares is a linear recurrence sequence), or more generally that the component-wise sum or product of two linear recurrence sequences is another linear recurrence sequence. (Hint: this is related to the fact that the sum or product of algebraic integers is again an algebraic integer.)
The Skolem-Mahler-Lech theorem concerns the set of zeroes of a given integer linear recurrence sequence. In the case of the Fibonacci sequence, the set of zeroes is pretty boring, just {0}. To give a somewhat trivial example, the linear recurrence sequence
;
has a zero set which is the even numbers . Similarly, the linear recurrence sequence
;
has a zero set , i.e. the odd numbers together with 0. One can ask whether more interesting zero sets are possible; for instance, can one design a linear recurrence system which only vanishes at the square numbers
? The Skolem-Mahler-Lech theorem says no:
Skolem-Mahler-Lech theorem. The zero set of a linear recurrence set is eventually periodic, i.e. it agrees with a periodic set for sufficiently large n. In fact, a slightly stronger statement is true: the zero set is the union of a finite set and a finite number of residue classes
.
Interestingly, all known proofs of this theorem require that one introduce the p-adic integers (or a thinly disguised version thereof). Let me quickly sketch a proof as follows (loosely based on the proof of Hansel). Firstly it is not hard to reduce to the case where the final coefficient
is non-zero. Then, by elementary linear algebra, one can get a closed form for the linear recurrence sequence as
where A is an invertible matrix with integer coefficients, and v, w are d-dimensional vectors with integer coefficients (one can write A, v, w explicitly in terms of
and
, but it is not necessary to do so for this argument). Since A is invertible, we can find a large prime p such that A is also invertible modulo p; for technical reasons we also need p to be larger than 2 so (any prime not dividing 2 det(A) will do). Let us now fix this p. The invertible matrices
over the finite field
take on only finitely many values, thus by the pigeonhole principle there must exist a finite
such that
, where I is the identity matrix.
This m is going to be the eventual period of the zero set; more precisely, for every , I claim that the modified zero set
is either finite, or equal to all of
(this will clearly imply the Skolem-Mahler-Lech theorem). To see this claim, suppose that this modified zero set is infinite for some r, thus
for infinitely any n. By construction of m, we can write for some integer-valued matrix B, thus
for infinitely many integers n, where
.
This identity makes sense in the (rational) integers , and hence also in the larger ring of p-adic integers
. On the other hand, observe from binomial expansion that P(n) can be expressed as a formal power series in p with coefficients polynomial in n:
.
Here the are polynomials with coefficients in the p-adic integers. Indeed, the binomial expansion of
contains terms involving a polynomial in
times
for natural number
. The number of times
divides
is
which grows slower than
since
was assumed to be larger than 2; hence each of the
can be built using only finitely many of the terms in the binomial expansion.
Because of this, the function extends continuously to a function
, such that
is a polynomial in n for each j. In other words, P is a uniform limit of polynomials in the p-adic topology. [Note that the Stone-Weierstrass theorem is not applicable here, because we are using p-adic valued functions rather than real or complex-valued ones.] What we need to show is that if P has infinitely many zeroes, then it vanishes everywhere (which is of course what we expect polynomial-like objects to do).
Now if for some
(either an integer or a p-adic integer, it doesn’t matter), one can then formally divide
by
(as in the factor theorem from high school algebra) to conclude that
for some continuous function Q which, like P, is a polynomial modulo
for each j, and whose “constant coefficient”
either vanishes, or has degree strictly less than the corresponding coefficient
of P. Iterating this fact, we eventually see that if P has infinitely many zeroes, then it contains a factor with vanishing constant coefficient, or in other words it is divisible by p. We iterate this fact again and conclude that if P has infinitely many zeroes then it must be divisible by arbitrarily many powers of p, and thus must vanish everywhere. This concludes the proof.
Now, the above proof clearly gives a quite effective and computable bound on the eventual period m of the zero set. By working somewhat harder, Evertse, Schlickewei, and Schmidt obtained an effective bound on how many exceptional zeroes there are – zeroes of one of these almost polynomials P which do not cause P to vanish entirely. But there appears to be no effective bound known as to how large these zeroes are! In particular, one does not even know how to decide whether this set is non-empty, thus we have
Open problem. Given an integer linear recurrence sequence (i.e. given the data
as integers), is the truth of the statement “
for all n” decidable in finite time?
(Note that I am only asking here for decidability, and not even asking for effective bounds.) It is faintly outrageous that this problem is still open; it is saying that we do not know how to decide the halting problem even for “linear” automata!
The basic problem seems to boil down to one of determining whether an “almost polynomial” (i.e. a uniform limit of polynomials) has an integer zero or not. It is not too hard to find the p-adic zeroes of P to any specified accuracy (by using the p-adic version of Newton’s method, i.e. Hensel’s lemma), but it seems that one needs to know the zeroes to infinite accuracy in order to decide whether they are integers or not. It may be that some techniques from Diophantine approximation (e.g. some sort of p-adic analogue of the Thue-Siegel-Roth theorem) are relevant. Alternatively, one might want to find a completely different proof of the Skolem-Mahler-Lech theorem, which does not use p-adics at all.
[Update, May 26: Typos, example, and full statement of SML theorem corrected.]
[Update, Sep 26, 2016: it was pointed out by Kamil Rychlewicz that the argument requires the prime p to be larger than 2.]

40 comments
Comments feed for this article
26 May, 2007 at 2:26 am
Johan Richter
There is a typo in your statement of the theorem, the “if” shoudl be “of”. (At least, the statement would make better sense than.)
26 May, 2007 at 5:01 am
Maurizio
There is also a typo about the recurrence with : the zeros are {2,6,10,…}, ie the numbers in the remainder class of 2 mod 4.
: the zeros are {2,6,10,…}, ie the numbers in the remainder class of 2 mod 4.
26 May, 2007 at 7:44 am
Terence Tao
Thanks for the corrections!
26 May, 2007 at 8:07 am
Emmanuel Kowalski
I’ve been very partial myself to the following “trivial” way of proving that a set is finite
without getting any more information at all: “A compact and discrete topological space
is finite”. This is clearly related to #2 and #3 above, and I find this to be often efficient
in (at least) understanding sophisticated finiteness theorems in number theory: they
are often obtained by combining two conditions, one of which looks like discreteness
and the other like compactness (but this is not always transferrable to a proof,
as far as I can see).
For instance the finiteness of ideal class group of number fields can be proved in this manner (using the adele/idele framework; the ideal class group being represented as a quotient of a compact group in such a way that the quotient topology is discrete). This is an interesting example also because in this case the proof can be made (and indeed, it was from the beginning) effective — the Minkowski bound from geometry of numbers gives an effective upper bound on the norm of ideals generating the ideal class group –, but it is effective in a non-practical way (it gives an exponential-time algorithm).
Incidentally, I’ve been wondering at some point what the analogue in “noncommutative geometry” of this simple statement could be. The best candidate I had what something
like : “any C^* algebra with unit which is equal to its enveloping von Neumann
algebra is finite dimensional”, but I don’t know it this is true (or if it makes sense!), the idea being that this means that any the first condition is analogue of compactness, and the second means “every measurable function is continuous”, so should be analogue
of discreteness.
In the paper of Evertse, Schlickewei and Schmidt, the main tool (if I remember right) is
Schmidt’s subspace theorem (or its generalizations), hence indeed clearly related to the Thue-Siegel-Roth theorem. Finding an effective version of this would thus solve
the problem — and many more besides…
26 May, 2007 at 8:41 am
Emmanuel Kowalski
P.S. Some typos in the previous comment:
(1) the second-to-last paragraph should read
Incidentally, I’ve been wondering at some point what the analogue in “noncommutative geometry” of this simple statement could be. The best candidate I had what something
like : “any C^* algebra with unit which is equal to its enveloping von Neumann
algebra is finite dimensional”, but I don’t know it this is true (or if it makes sense!). The idea is that the first condition is an analogue of compactness, and the second means “every measurable function is continuous”, so should be analogue of discreteness.
(2) I don’t know who first gave the proof of the finiteness of the ideal class group in the
manner which I mentioned; maybe Chevalley when introducing ideles? It is
explained at least in the chapter on global fields in the proceedings of the Brighton
conference on Algebraic Number Theory (edited by Cassels and Fr\”olich).
26 May, 2007 at 4:00 pm
Top Posts « WordPress.com
[…] Open question: effective Skolem-Mahler-Lech theorem The Skolem-Mahler-Lech theorem in algebraic number theory is a significant generalisation of the obvious statement that […] […]
27 May, 2007 at 7:36 am
Terence Tao
Dear Emmanuel,
Very interesting remarks! I might classify the “compact + discrete -> finite” method as being more in the spirit of #1, though. If one had a sufficiently quantitative measure of both compactness and discreteness, one could hope to obtain a quantitative measure of finiteness; for instance, if one is in a metric space, and one has a bound for metric entropy numbers (how many balls of radius are needed to cover the space) and minimal separation between elements (i.e. uniform discreteness), then one easily gets a bound on the cardinality. Things get harder when the topology is not metrisable or the discreteness is not uniform, though; even for closed subsets of [0,1] one already sees the weak Konig lemma come up in the compactness theory (i.e. Bolzano-Weierstrass) which suggests, at minimum, that the quantitative bounds extractable from this method are likely to be terrible.
are needed to cover the space) and minimal separation between elements (i.e. uniform discreteness), then one easily gets a bound on the cardinality. Things get harder when the topology is not metrisable or the discreteness is not uniform, though; even for closed subsets of [0,1] one already sees the weak Konig lemma come up in the compactness theory (i.e. Bolzano-Weierstrass) which suggests, at minimum, that the quantitative bounds extractable from this method are likely to be terrible.
I don’t have anything intelligent to say about the noncommutative version, but perhaps others will…
27 May, 2007 at 7:43 pm
Jordan Ellenberg
Akshay pointed this post out to me with the comment that it is reminiscent of Chabauty. That seems right. Chabauty’s theorem applies to curves X over Q with the property that genus(X) not give any bound on the height of a point on your curve. So again, one has a bound on the number of “exceptional” (which in this case means “rational”) points, but not a bound on their size.
27 May, 2007 at 7:45 pm
Jordan Ellenberg
Um, most of that comment was eaten for reasons not transparent to me. Briefly: Chabauty’s theorem, under some hypotheses, tells you that the rational points on a curve X are supported on the zeroes of some p-adic analytic functions. As in your post, with some work you can get a bound on the number of such zeroes (see e.g. Coleman, “Effective Chabauty”, and later work of Lorenzini-Tucker) but, again as above, there seems no way to leverage this into a bound on the height of a rational point.
28 May, 2007 at 6:49 am
Felipe Voloch
Skolem-Mahler-Lech and Chabauty are the same thing, actually. Chabauty extended ideas of Skolem from linear tori to abelian varieties. This is explained in e.g. Borevich-Shafarevich or Cassels book on local fields.
28 May, 2007 at 7:34 am
Terence Tao
Dear Jordan and Felipe, thank you for your comments! (Jordan: wordpress tends to eat anything which looks like html, in particular anything involving < and > can get mangled.)
I am very happy to hear about the connection between Skolem-Mahler-Lech and Chabauty. A really nice prize in this area would be an effective version of Faltings’ theorem (i.e. effective bounds on the heights of the rational points; I believe one already has effective bounds on the cardinality, and the problem is related to either #2 or #3 above). I understand that Chabauty’s theorem is like a baby version of Faltings’ theorem, so there is now a natural progression of difficulty from effective SML to effective Chabauty to effective Faltings, though it seems that even the first step looks quite hard.
29 May, 2007 at 7:08 am
A
“ineffective bound – a bound which is provably finite, but which cannot be computed!”
Are ineffective bounds uncomputable, in the sense that Turing might have intended, or have they simply not been computed in the proof?
Thanks,
A
29 May, 2007 at 8:42 am
Terence Tao
Dear A,
That is essentially correct, or more precisely an ineffective bound is one for which we do not know how to compute in the sense of Turing, even after close inspection of the proof. It may be, however, that new proofs may provide an effective bound on the same quantity.
To give a somewhat artificial example of an ineffective bound, let n be the first even number larger than 2 that cannot be expressed as the sum of two primes, or 0 if no such N exists (i.e. if the even Goldbach conjecture is true). Regardless of whether the Goldbach conjecture is true or false, this number n is clearly finite. However, the argument provides no effective bound n < N on the size of n. If it did, then the Goldbach conjecture would be decidable in finite time (we would simply verify whether all even numbers between 4 and N are the sum of two primes; if they are, and n < N, then the Goldbach conjecture must be true.)
1 June, 2007 at 3:51 am
martin hofmann
Re halting problem for “linear automata”: couldn’t one compute the eigenvalues of the matrix A first;
if they all have absolute value below 1 then we will get 0 eventually.
if the largest and the second largest eigenvalue (by absolute value) have different absolute value then the largest eigenvalue will dominate the behaviour and it should be possible to compute effectively when this happens. (zeroes could only occur prior to that point)
if the k largest eigenvalues (by absolute value) have equal absolute value then we could look at their arguments. I believe (this may well be wrong) that the argument of a complex solution of a real polynomial must be a rational fraction of 2*pi (because of the sum of angles in a polylateral).
By looking at the least common denominator of those fractions one could find out how close to each other their respective
powers could possibly get and once the contributions of smaller eigenvalues peter out one can again exclude the possibility of a zero.
Does that make some sense?
1 June, 2007 at 10:54 am
Kousha Etessami
It is worth pointing out that,
if one adopts a very rigid notion of “effectiveness”,
then Blondel and Portier (2002)
give a simple proof that:
“The presence of a zero in an integer linear recurrent sequence is NP-hard to decide”,
(Lin. Algebra and Its Applications, 351-352, pp. 91-98, 2002.). The proof is based on an old
automata-theoretic argument by Stockmeyer and Meyer.
The result applies already to non-negative
linear recurrence sequences (LRSs), where
the sequence is
x_i = u^T A^i v , i = 0,1,2,….
for a given non-negative dxd matrix A, and
given non-negative vectors u and v.
(In fact, if suffices to let u, A, and v, all have
entries in {0,1}.)
It is easy to see that for such non-negative
LRSs there is also an NP upper bound,
so this very restricted problem is NP-complete.
A simple corollary of the
NP-hardness proof is
the following lower bound: there is a family
of (non-negative) LRSs, L_n,
n=1,2, …, of
“encoding size” O(n)
(the coefficients are given in binary, etc.)
such that, for every n,
the sequence L_n does contain a zero,
but the smallest index for a zero is
2^{Omega(n)}.
(In other words, there is an “exponential”
lower bound on the location of the first zero
in the non-negative case.)
So, … perhaps a way to
gradually gain a better understanding
for the general LRS case (where the matrix
A can have both positive and negative entries)
would be to answer the following
Question: Is there a family of LRSs, L’_n,
n=1,2,…, of size O(n), such that
for every n, the sequence L’_n contains a zero,
but the smallest index for a zero is
2^{2^{Omega(n)}} ?
(Perhaps it is not hard to answer this affirmatively.
If so, then replace double-exponential by
triple-exponential, …. non-elementary,…
non-primitive-recursive,… etc.)
Even if one believes that an effective
Skolem-Mahler-Lech theorem should exist,
it is not at all clear (at least not to me)
what the right conjecture for the bound should be.
There is a lot of motivation,
in particular for applications in computer science,
for finding a small upper bound if one exists.
On the other hand, if one can show an
astronomical (e.g., non-elementary) lower bound,
then, at least from an applied perspective,
the decidability question becomes a lot less relevant.
2 June, 2007 at 2:03 am
martin hofmann
I try to make my suggestion a bit more precise. are the eigenvalues of A ordered by decreasing absolute value, so
are the eigenvalues of A ordered by decreasing absolute value, so 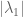 is largest then
is largest then
If
where the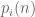 are polynomials in n of degree less than the (algebraic) multiplicity of
are polynomials in n of degree less than the (algebraic) multiplicity of 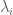 .
.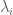 is a root of the real characteristic polynomial of A. I claim that therefore
is a root of the real characteristic polynomial of A. I claim that therefore 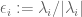 is a d-th root of unity.
is a d-th root of unity.
Each
Thus, we have
So, by distinguishing cases modulo n we are lead to deciding whether or not an expression of the form
where the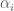 are positive real numbers and the
are positive real numbers and the 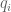 are complex polynomials in n, has a zero.
are complex polynomials in n, has a zero.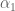 is the largest we can effectively compute
is the largest we can effectively compute 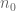 after which no more zeros can occur. Such
after which no more zeros can occur. Such 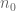 must be beyond the zeros of the
must be beyond the zeros of the 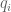 and be such that the contribution of the summands with
and be such that the contribution of the summands with 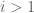 becomes negligible in view of the exponential gap between the summand i=1 and the later ones.
becomes negligible in view of the exponential gap between the summand i=1 and the later ones. so
so 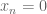 for large n because
for large n because 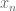 is an integer.
is an integer.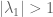 and
and  then
then 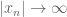 and we can compute a bound after which no more zeros can be expected from the polynomials
and we can compute a bound after which no more zeros can be expected from the polynomials 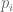 and the
and the 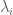 .
.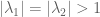 and (for simplicity)
and (for simplicity) 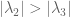
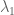 and
and  are roots of the characteristic polynomial of A their complex argument must be an integer multiple of
are roots of the characteristic polynomial of A their complex argument must be an integer multiple of  . This means that
. This means that 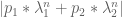 is either
is either  and therefore eventually dominates the contribution of the smaller eigenvalues or 0 which would occur periodically and once could then look recursively at the situation at smaller eigenvalues. I have here assumed that the coefficients
and therefore eventually dominates the contribution of the smaller eigenvalues or 0 which would occur periodically and once could then look recursively at the situation at smaller eigenvalues. I have here assumed that the coefficients  and
and 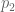 are constants rather than polynomials in n. The hope would be that a similar argument could be carried out in that more general case.
are constants rather than polynomials in n. The hope would be that a similar argument could be carried out in that more general case.
Assuming that
This does not contradict Kousha’s comments: It may well be that the bounds so obtainable are quite large and therefore the procedure becomes inefficient in practice.
PS:
Now, if
If
If
then since both
2 June, 2007 at 3:21 pm
Terence Tao
Dear Martin,
Thanks for your suggestions. Unfortunately, it is not the case that the argument of an algebraic integer is always a d^th root of unity. Consider for instance the number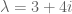 , which solves the equation
, which solves the equation 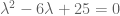 but whose argument has phase
but whose argument has phase  , which is a transcendental multiple of
, which is a transcendental multiple of 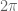 . Once there are multiple transcendental phases at the eigenvalues of the maximum magnitude, it is not clear how to proceed (though, as I said in my post, it may be that some tools from Diophantine approximation become relevant).
. Once there are multiple transcendental phases at the eigenvalues of the maximum magnitude, it is not clear how to proceed (though, as I said in my post, it may be that some tools from Diophantine approximation become relevant).
3 June, 2007 at 12:47 pm
Kousha Etessami
Regarding the latest comments, another reference worth mentioning
is the following fairly recent survey:
“Skolem’s problem: on the border between decidability and undecidability”,
authors: V. Halava, T. Harju, M. Hirvensalo, J. Karhumaki,
Tech report 683, Turku Unviersity Computer Science, 2005.
(Link:
http://www.tucs.fi/publications/insight.php?id=tHaHaHiKa05a )
They survey the known decidable cases, and in particular they use
spectral techniques (roughly related to Martin’s suggestions) combined
with Baker’s powerful theorem from
transcendental number theory on linear independence of logarithms
of algebraic numbers;
but all this only allows them to solve some special cases,
such as the case where the linear recurrence has length at most 5
(plus some cases where the eigenvalues of the correlated matrix
have restricted structure).
4 June, 2007 at 8:26 am
Terence Tao
Dear Kousha,
Thanks for the link to the interesting survey! It is remarkable how even Baker’s theorem only gets as far as length 5 recurrences. Perhaps this indicates that transcendence theory is in fact not quite the right tool for the task, and one needs to exploit the algebraic structure more…
6 June, 2007 at 9:16 am
Joel Ouaknine
As an aside, another interesting source of “ineffective bounds” arises from the theory of well-quasi orders, such as Higman’s Lemma or the Robertson-Seymour theorem. For example, Robertson-Seymour easily implies that there is a finite set S of graphs such that a given graph G is planar iff it does not have any graph in S as a minor. Now, of course, in this instance Kuratowski’s theorem tells us in fact that S precisely consists of K_{3,3} and K_5, but Robertson-Seymour could not even give us a bound on the cardinality of S, other than to say it was finite.
In general, there are many other such examples from the theory of algorithms in which no equivalent “Kuratwoski’s theorem” is known to exist. There are even cases in which no effective bounds can be given at all. For example, the set of reachable configurations of a “lossy counter machine” (a certain kind of faulty Turing machine) can always be represented by a finite automaton, however it is known that that automaton cannot in general be computed from the lossy counter machine, and in fact the minimum number of states of the representing automaton, while finite, cannot be computed either.
8 June, 2007 at 6:58 am
martin hofmann
Dear Terence,
thank you for taking the time to dispel my somewhat naive attempts at
using eigenvalues. A triangle with 2 angles equal to each other is
unfortunately not in general equilateral…
Now I was trying to understand your p-adic proof to see what exactly
is the measure going down in this hypothetical infinite regress. In
the techreport that Kousha pointed out they make a big deal of these
binomial coefficients and their respective v_p-values. In view of your
proof this looks like unnecessary hocus pocus. On the other hand, while
your argument is completely transparent to me when
P(n) mod p^j is a polynomial with integer
coefficients, I cannot yet see how it works when P(n) mod p^j
has fractional coefficients (perhaps with denominators = 0 mod p) like in
P(x) = choose(x,3) and p=3.
8 June, 2007 at 7:35 am
Felipe Voloch
Martin,
You are free to choose p, given the recurrence, and avoid its presence in denominators. On the other hand, the p-adic proof gives a bound on the number of solutions, when finite and it depends on p. To get the best bound sometimes requires some careful estimates or “hocus pocus”.
8 June, 2007 at 8:49 am
Terence Tao
Dear Emmanuel,
I asked my operator algebra colleagues here at UCLA about your question, and am enclosing a response from Sorin Popa and Narutaka Ozawa. Tim Austin also commented that the original formulation of the question can be answered in the negative: the ring of continuous is itself a von Neumann algebra, for example, being just
is itself a von Neumann algebra, for example, being just  .
.
functions on the Cech-Stone compactification of
—
Kowalski’s question can in fact be posed
 of A.
of A.
in two ways, on which I comment below.
Note first of all that requiring A to be
“equal” or merely isomorphic to its enveloping vN algebra
means already that the C* algebra A
is a W* algebra, i.e. an algebra that
can be represented faithfully on a Hilbert space as a vN algebra
and that by Sakai’s theorem this is equivalent to the fact that
it has predual as a Banach space. Also, Sakai’s theorem
identifies the enveloping vN algebra with the (Banach) bidual
1 Asking that the C*-algebra A be “equal” to (which is equal to the enveloping vN algebra),
(which is equal to the enveloping vN algebra), ,
,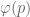 as close to 0
as close to 0 prevents that from happening.
prevents that from happening.
its bidual
in the sense that the canonical embedding of A into the bidual
is an equality. This trivially implies the algebra is finite
dimensional, since it is very easy to see that if it is
infinite dimensional then A contains a
non-normal state (i.e. a state which fails to be
completely additive on mutually orthogonal
projections), in fact even a “singular” state
i.e. a state with the property that it is identically 0
under projections p with
as you want. Or
2 Asking that the C* algebra A be isomorphic to its bidual .
.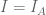 denotes a set of largest cardinality
denotes a set of largest cardinality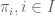 , in the vN algebra A, then
, in the vN algebra A, then
 has strictly larger cardinality than
has strictly larger cardinality than 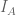
This also implies that A is finite dimensional, but
the proof is a bit more difficult: one can show that
if
such that there exist mutually orthogonal non-zero
projections
(unless of course A is fin dim).
8 June, 2007 at 9:41 am
Emmanuel Kowalski
Thanks for getting this information! Now I’ll try to understand the details.
I also wish I could get some interesting application… (At the time I was thinking vaguely about such questions, I was optimistically hoping there might be some tough finiteness questions in number theory, such as that of Tate-Shafarevich groups, which would be approachable by noncommutative geometry).
8 June, 2007 at 10:55 am
David Speyer
Here is a basic question, continuing the naive eigenvalue approach. Suppose that a_1, …, a_n are a collection of algebraic integers closed under the action of Gal(Q^{alg}/Q). Suppose that a_i/a_j is never a root of unity for i not equal to j. Does there always exist a norm ||, either archimedean or non-archimedean, such that the maximum of |a_1|, …, |a_n| is unique?
I find it completely implausible that such a thing should be true, but I don’t have a counter-example and it is true for n=2. (Kronecker’s Lemma applied to a_1/a_2, see for example Borevich and Shafarevich, “Number Theory”, Section 2.3 Thrm 2.) So I am curious whether anyone here has a counter-example.
The point is that, if the a_i are the eigenvalues of A, then whenever such a norm exists, we can give explicit bounds past which can’t be zero. For example, it is hard to bound (3+4i)^n-(3-4i)^n away from zero in the archimedean norm, but quite simple in the (1+2i)-adic norm.
8 June, 2007 at 11:03 am
David Speyer
Grrr, why do I always think of the good counterexamples after asking the questions?
(1+2i)*(2+3i), (1+2i)*(2-3i), (1-2i)(2+3i), (1-2i)(2-3i)
14 June, 2007 at 6:30 am
martin hofmann
Apparently one can use the Baker’s theorem to determine a bound on n
beyond which it can no longer happen that a nonzero but small contribution of the dominant eigenvalues cancels against the contribution of the smaller eigenvalues.
What seems difficult is when the contribution of the dominant eigenvalues is zero itself.
So, one is essentially lead to the following question: let exp(i phi_j) and exp(i theta_j) be algebraic numbers for j=1..ell. Let
Z = {n | exp(i (phi_1 + n theta_1)) + … + exp(i (phi_ell + n theta_ell)) = 0}
Can we effectively compute a number N so that Z is either infinite or contained in {0..N} ?
It would be enough to answer the question for exp(i (phi_j + n theta_j)) replaced by cos(phi_j + n theta_j) because eigenvalues come in conjugate pairs.
29 October, 2007 at 6:04 am
The Funny One
Hey Kousha,
Thanks for providing the link to the amazing survey, i was really impressed by it and the things people think of these days, thought it was just me.
20 January, 2008 at 2:25 pm
Navtej Kohli
Wish i had the talent to write such posts.
2 March, 2009 at 1:54 pm
Qiaochu Yuan
It occurred to me today that it’s possible to embed the Frobenius coin problem into this problem, as follows: the number of ways to represent a non-negative integer as a non-negative sum of a fixed set of non-negative integers has a rational generating function, equivalently, is a sequence that satisfies an integer linear recurrence. The coin problem asks for the largest number such that no such representations exist, i.e. the largest zero of such a sequence. And the coin problem is known to be NP-hard (in general) as well (although the existence of zeroes is trivial here). Perhaps this would be an instructive special case?
2 March, 2009 at 2:41 pm
davidspeyer
That’s interesting, but it isn’t hard to give a bound in the coin case — if I recall correctly, the product of the coin values works. The NP-hard problem is determining the actual position of that last zero. Whereas in Skolem-Mahler-Lech, we seem to actually have a computability issue — there is no known bound at all.
4 September, 2009 at 4:30 am
The Orbit Problem « Gödel’s Lost Letter and P=NP
[…] this a theorem? Terry Tao raises a related question in his famous blog on recurrence sequences. He gives it as an example of a question that we should know the answer to, […]
26 December, 2009 at 6:14 am
Mathematical Embarrassments « Gödel’s Lost Letter and P=NP
[…] linear recursion zero problem. An ME due to Tao is a problem about linear recurrences. Given a linear recurrence over the […]
18 March, 2010 at 5:22 pm
The Skolem-Mahler-Lech theorem « Cam's Blog
[…] proof of the SML theorem that I’ll give was essentially lifted from Terrence Tao’s blog. He in turn essentially lifted it from this paper of […]
11 September, 2010 at 8:56 pm
Vagabond
Incidentally a lemma due to Turan comes very close to proving Skolem Mahler Lech theorem. Its says if one knows the values of an exponential polynomial along an n length AP then one can find an estimate of it at the n+1 th point. Applied to the the specific case under consideration ( i.e. an exponential polynomial of order n) it says if the exponential polynomial vanishes at an arithmetic progression of length n then it vanishes on the complete arithmetic progression. So Szemeredi’s theorem tells us that the structure of the zero set has to be union of complete AP plus a set of dnsity zero set ( having no AP of length n). Though it does not prove Skolem Mahler Lech theorem it’s tantalizingly close and provides the extra information about the geometry of the zero sets …. that the exceptional set do not have an n length AP and using estimates from Ramsey theory one can find a bound on how many zeros can be there in an interval ?
13 September, 2010 at 6:40 pm
Richard Stanley
I am curious about generalizations of Mahler-Skolem-Lech. I believe it is still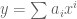 is algebraic (satisfies a polynomial equation whose coefficients are polynomials in
is algebraic (satisfies a polynomial equation whose coefficients are polynomials in  ) or more generally D-finite (satisfies a linear differential equation whose coefficients are polynomials in
) or more generally D-finite (satisfies a linear differential equation whose coefficients are polynomials in  ), then is the set of
), then is the set of  ‘s for which
‘s for which 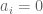 eventually a union of arithmetic progressions? This is known to be false for algebraically differential series
eventually a union of arithmetic progressions? This is known to be false for algebraically differential series  , i.e.,
, i.e.,  satisfies an equation that is a polynomial in
satisfies an equation that is a polynomial in  .
.
open for algebraic power series or even D-finite power series. Is this correct?
In other words, if
2 January, 2011 at 10:40 am
Peter Komjath
This paper may be of interest (sorry if already mentioned):
Bruce E. Litow: A Decision Method for the Rational Sequence Problem Electronic Colloquium on Computational Complexity (ECCC) 4(55): (1997)
7 April, 2013 at 3:54 am
From letter exchange to blog exchange | To All You Zombies
[…] https://terrytao.wordpress.com/2007/05/25/open-question-effective-skolem-mahler-lech-theorem/, retrieved 7.4.2013 […]
7 July, 2014 at 2:20 am
The subspace theorem approach to Siegel’s theorem on integral points on curves via nonstandard analysis | What's new
[…] may be bounded effectively; cf. the situation with the Skolem-Mahler-Lech theorem, discussed in this previous blog post.) Once again, the lower bound here is basically sharp except for the factor and the implied […]
7 November, 2021 at 11:23 am
Caleb Stanford (@calebstanford4)
Minor correction: in your definition of LRS, you need to require that . Otherwise, you allow eventually-periodic sequences like
. Otherwise, you allow eventually-periodic sequences like  for which the Skolem-Mahler-Lech theorem as stated does not hold (the zeros here are not a union of full residue classes).
for which the Skolem-Mahler-Lech theorem as stated does not hold (the zeros here are not a union of full residue classes).
[Corrected, thanks – T.]