For the past several years, my good friend and fellow Medalist Timothy Gowers has been devoting an enormous amount of effort towards editing (with the help of June Barrow-Green and Imre Leader) a forthcoming book, the Princeton Companion to Mathematics. This immense project is somewhat difficult to explain succinctly; a zeroth order approximation would be that it is an “Encyclopedia of mathematics”, but the aim is not to be a comprehensive technical reference, nor is it a repository of key mathematical definitions and theorems; it is neither Scholarpedia nor Wikipedia. Instead, the idea is to give a flavour of a subject or mathematical concept by means of motivating examples, questions, and so forth, somewhat analogous to the “What is a …?” series in the Notices of the AMS. Ideally, any interested reader with a basic mathematics undergraduate education could use this book to get a rough handle on what (say) Ricci flow is and why it is useful, or what questions mathematicians are trying to answer about (say) harmonic analysis, without getting into the technical details (which are abundantly available elsewhere). There are contributions from many, many mathematicians on a wide range of topics, from symplectic geometry to modular forms to the history and influence of mathematics; I myself have contributed or been otherwise involved in about a dozen articles.
If all goes well, the Companion should be finalised later this year and available around March 2008. As a sort of “advertising campaign” for this project (and with Tim’s approval), I plan to gradually release to this blog (at the rate of one or two a month) the various articles I contributed for the project over the last few years. [As part of this advertising, I might add that the Companion can already be pre-ordered on Amazon.]
I’ll inaugurate this series with my article on “wave maps”. This describes, in general terms, what a wave map is (it is a mathematical model for a vibrating membrane in a manifold), and its relationship with other concepts such as harmonic maps and general relativity. As it turns out, for editing reasons various articles solicited for the Companion had to be removed from the print edition (but possibly may survive in the on-line version of the Companion, though details are unclear at this point); Tim and I agreed that as wave maps were not the most crucial geometric PDE that needed to be covered for the Companion (there are other articles on the Einstein equations and Ricci flow, for instance), that this particular article would end up being one of the “deleted scenes”. As such, it seems like a logical choice for the first article to release here.
What's new 
16 comments
Comments feed for this article
30 August, 2007 at 3:26 pm
locke
Terry, I think you may underestimate the value of the companion to research mathematicians. In particular, if the articles are similar in scope and spirit to yours on wave maps, then I can see this being a fantastic resource for getting snapshots into other (many times impenetrable without significant effort) fields.
30 August, 2007 at 10:14 pm
Mike
Hi Mr Tao,
Thanks for posting this article on wave maps. It looks within reach of my single-semester PDE knowledge (especially the KE/PE technique and limits of influence), yet describes open areas of research. I’ll look forward to further deleted scenes.
I’ve read Mr Gowers’ articles on his discussions page, and his articles on analysis really struck a chord with my experience those types of classes. Most importantly, his ideas from the “defining a definition” make him seem like just the person to edit this sort of text (at least from this undergrad’s POV).
31 August, 2007 at 2:44 am
sgrajeev
The wave map looks like what we call a `non-linear sigma model’ (awkward terminology for sure) in physics. Is it the same thing?
If the target is SU(2) =S^3 this is the equation for the Goldstone bosons of the chiral model, which are the pi mesons. They were first described (Gell-Mann) by the linear sigma-model in which the field took values in R^4, the fourth direction being called sigma. Then it was found (Gursey) that a better description was to get rid of a degree of freedom by restricting to the sphere, which came to be called the non-linear sigma model.
31 August, 2007 at 8:15 am
Terence Tao
Dear sgrajeev,
That is correct; wave maps (at least into targets such as SU(2)) are what mathematicians call the (classical) nonlinear sigma model; as far as I know, the mathematicians who study wave maps have not attempted to look at the corresponding QFT (which would be a much more complicated version of the
model, which is the quantum version of what mathematicians call the cubic nonlinear wave equation). I think the renaming of this equation was designed to deliberately invoke the analogy with harmonic maps. (And nowadays there are also “Schrodinger maps”, which are to the free Schrodinger equation as wave maps are to the free wave equation, or harmonic maps are to Laplace’s equation.) Also, we are interested in more general targets than the sphere, for instance hyperbolic space is particularly interesting for its connections to general relativity and also because this is likely to be the first non-flat target for which we will be able to establish a large data global regularity result.
31 August, 2007 at 6:35 pm
Pavel Krapivsky
Dear Terry,
It is late and I may be missing something, but it looks as the 1st displaced equation in your “wave maps” article contains a typo (u appears twice on the right-hand side); analogous misprint is in equation (2).
Best wishes for the weekend, Paul
1 September, 2007 at 8:13 am
Anonymous
Are there results in the opposite direction? i.e., that smooth data will evolve into singularities when the target is positively curved.
Physically, its is clear that a Skyrme soliton (winding number one map S^3–>S^3) will evolve as a wave map into a point-like singularity.
(Follows from scaling). Is it interesting to prove rigorously that such singularities develop for `large’ data? Or, perhaps it is too obvious.–Rajeev
1 September, 2007 at 12:22 pm
Adam
Dear Terry,
By the more complicated version of the \Phi^4 model, do you mean
the famous 1964 Higgs field theory for electroweak unification? Another
new supercollider is being built, at CERN, to find a particle it predicts,
the Higgs boson, also referred to as “God’s particle” by some scientific
magazines. E. Witten wrote about this in a recent BAMS article.
This may be the last frontier of experimentally verifiable serious
theoretical physics.
Cheers,
Adam
1 September, 2007 at 8:16 pm
Anon
The article was an enjoyable read – though in addition to those typos previously pointed out, on page 5 it should be (R x R^n) instead of (R -> R^n), and “at a distance further than ct0 from x0” instead of “t0 from x0”.
4 September, 2007 at 8:58 am
Terence Tao
Dear Pavel and Anon: thank you for the corrections!
Dear Anonymous: There are two recent papers (by Rodnianski-Sterbenz and Krieger-Schlag-Tataru) that establish singularity formation for certain large data for wave maps into the sphere:
http://arxiv.org/abs/math/0605023
http://arxiv.org/abs/math/0610248
The two results are slightly different; the RS paper gives a stable blowup but does not have precise asymptotics, whereas the KST paper allows one to prescribe the asymptotics to some extent, but is a very unstable blowup (the initial data has to be extremely special).
Dear Adam: I am not so familiar with the Higgs model, but I believe it is slightly different, more analogous to coupling a scalar field to a Yang-Mills model than to the wave maps model (which does not involve a scalar field, but instead involves a field that takes values in a target manifold). There are broad similarities between all of these equations, though. For instance, there is a gauge symmetry in the wave maps equation (coming from a selection of an orthonormal frame on the tangent bundle of the target, or more precisely the pullback of that bundle by the wave map) which is very analogous to the gauge symmetry of a Yang-Mills model.
5 September, 2007 at 6:38 am
McGuigan
Thanks for sharing your interesting article on wave maps.
General relativity itself has a formulation in terms of wave maps from R^3 to R x SL(3,R)/SO(3) described by DeWitt in
http://prola.aps.org/abstract/PR/v160/i5/p1113_1
where he says:
“Einstein’s equations are revealed as geodesic equations in the manifold of 3-geometries, modified by the presence of a “force term.” The classical phenomenon of gravitational collapse shows that the force term is not powerful enough to prevent the trajectory of space-time from running into the frontier.”
These type of wave maps form singularities which are the same as those that occur in Einstein’s equation.
17 September, 2007 at 12:32 pm
Doug
Hi Terence,
I have been thinking about this phrase in this post ‘PCM “deleted scene”: Wave maps‘:
“… on what (say) Ricci flow is and why it is useful …”
and from the post ‘Simons Lecture III: Structure and randomness in PDE’
“The most famous recent example of the use of parabolic flows to establish geometric structure from topological objects is, of course, Perelman’s use of the Ricci flow applied to compact 3-manifolds with arbitrary Riemannian metrics …”
Questions:
If the parabolic flow is also in motion, then may the flow be a parabolic catenary?
If the flow is catenary in motion, then perhaps there exists an equivalent helix flow?
If the flow is helical in motion, then perhaps these may be geodesic trajectories?
Reasons for this speculation:
1 – At Strings 07, Urs Wiedemann [CERN] ‘Jet quenching in string theory and heavy ion collisions’ commented: “Our task: find catenary” in slide 38 of 38 [last line].
Click to access wiedemann.pdf
[These could be elliptic or hyperbolic rather than the more common parabolic catenary.]
2 – Rolling parabolic curves are catenaries.
3 – The catenoid and helicoid are in isometry, so there is probably an equivalent helix for each catenary.
4 – The helix is associated with trajectories.
a – Gun barrel rifling.
b – David Hestenes, ‘The Kinematic Origin of Complex Wave Functions’ discusses “Zitterbewegun interactions” and “helical lightlke [electromagnetic?] trajectory”
Click to access Kinematic.pdf
c – “Unseen curled-up dimensions” [or equivalent wording] of:
i – Lisa Randall, Raman Sundrum, ’A Large Mass Hierarchy from a Small Extra Dimension’.
ii – Nima Arkani-Hamed, Savas Dimopoulos, Gia Dvali. ’The Hierarchy Problem and New Dimensions at a Millimeter’.
d -Tamar Basar, Geert Jan Olsder, ‘Dynamic Noncooperative Game Theory’, chapter 8.
e – A possible link between continuous motion and the concept of continuous transformations of Sophus Lie.
17 September, 2007 at 12:55 pm
Terence Tao
Dear Doug,
The term “parabolic” when applied to PDEs has a rather technical meaning which is only indirectly connected to the parabola as a curve. Because the equations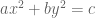
, 
, and 
describe an ellipse, parabola, and hyperbola respectively, the three PDE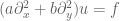 
, 
, and 
were labeled elliptic, parabolic, and hyperbolic PDE respectively. Later on, this classification of PDE was generalised to situations in which no ellipse, parabola, or hyperbola is visible at all.
Solutions to parabolic flows tend to become smoother and gradually flatter over time. For instance, the fundamental solution to the heat equation
on 
– which is the most basic of all the parabolic equations – is given by 
, thus at each time t, the solution is a Gaussian, whose amplitude decreases (and whose width increases) over time. There are some faint connections with parabolae (for instance, the level sets of the phase 
are parabolae) but I would in general caution against reading too much into the term “parabolic”.
21 September, 2007 at 1:16 pm
Doug
Hi Terence,
I think that I understand your comment about the term parabola encompassing more than a single curve in the context of PDE.
It is somewhat similar to there being more than one catenary:
– parabolic catenary [usually referred to as simply catenary]
– elliptic catenary
– hyperbolic catenary
– and
– perhaps other as yet unclassified catenaries.
However, I think that Urs Wiedemann and the others listed above may not realize the possibly significant relation of catenary and helix [as a geodesic]:
1 – on Earth, generally squirrels oppose gravity by climbing the cylindrical tree trunk in a helical manner – moving from one unfixed point to another.
2 – planets appear to revolve around a moving sun in a helical trajectory about a virtual cylinder – moving from one unfixed point to another – although often the sun is visualized as stationary and the planetary orbits as ellipses.
3 – bridges on earth tend to form a catenary between to two fixed points.
Thus there may be a gravity relation with both catenary and helix.
The ubiquity of the helix at so many different scales [gauges] seems to suggest the conveyance of information in many different forms.
Mathematical music example:
Pitch space of music [and probably radio waves and electromagnetic {EM}waves in general] have been described as both linear and helical.
“M.W. Drobisch (1855) was the first to suggest a helix (i.e. the spiral of fifths) to represent octave equivalence and reoccurrence (Lerdahl, 2001), and hence to give a model of pitch space.”
“… Euler (1739), Hermann von Helmholtz (1863/1885), Arthur von Oettingen (1866), Hugo Riemann (who should not be confused with the famous mathematician Bernhard Riemann), and Christopher Longuet-Higgins (1978) have modeled pitch relationships using two-dimensional (or higher-dimensional) lattices …”
http://en.wikipedia.org/wiki/Pitch_space
I do recognize that I may be wrong [by over-generalizing], but the helix is also involved transmitting information in nucleic acids and proteins and in EM solenoids.
9 October, 2007 at 8:15 pm
Doug
Hi Terence,
RE: Einstein … “the Einstein equations” and “general relativity”
This question is more about the special relativity E=mc^2.
Most of us have been taught that c is a constant.
What if c is a constant extrema [maximum]?
Is this subtle difference signifcant in both mathematics and physics?
Example: E=m*(MAX(a)), where MAX(a)=c^2
This would seem to imply that
E=(1/2)*m*(MAX(v))^2, where MAX(v)=c*2^(1/2)
I raise this question due to my interest in game theory.
2 June, 2008 at 10:08 am
Global regularity of wave maps III. Large energy from R^{1+2} to hyperbolic spaces « What’s new
[…] the last nine years or so, I have been working on and off on the global regularity problem for wave maps . The wave map equation is a nonlinear generalisation of the wave equation in which the unknown […]
29 June, 2008 at 7:31 am
Global regularity of wave maps IV. Absence of stationary or self-similar solutions in the energy class « What’s new
[…] In the first installment of this project, I was able to establish the global existence of smooth wave maps from 2+1-dimensional spacetime to hyperbolic space from arbitrary smooth initial data, […]