In the previous post, I discussed how an induction on dimension approach could establish Hilbert’s nullstellensatz, which we interpreted as a result describing all the obstructions to solving a system of polynomial equations and inequations over an algebraically closed field. Today, I want to point out that exactly the same approach also gives the Hahn-Banach theorem (at least in finite dimensions), which we interpret as a result describing all the obstructions to solving a system of linear inequalities over the reals (or in other words, a linear programming problem); this formulation of the Hahn-Banach theorem is sometimes known as Farkas’ lemma. Then I would like to discuss some standard applications of the Hahn-Banach theorem, such as the separation theorem of Dieudonné, the minimax theorem of von Neumann, Menger’s theorem, and Helly’s theorem (which was mentioned recently in an earlier post).
To simplify the exposition we shall only work in finite dimensions and with finite complexity objects, such as finite systems of linear inequalities, or convex polytopes with only finitely many sides. The results can be extended to the infinite complexity setting but this requires a bit of care, and can distract from the main ideas, so I am ignoring all of these extensions here.
Let us first phrase a formulation of the Hahn-Banach theorem – namely, Farkas’ lemma – which is deliberately chosen to mimic that of the nullstellensatz in the preceding post. We consider systems of linear inequalities of the form
where lies in a finite-dimensional real vector space, and
are affine-linear functionals. We are interested in the classic linear programming problem of whether such a system admits a solution. One obvious obstruction would be if the above system of inequalities are inconsistent in the sense that they imply
. More precisely, if we can find non-negative reals
such that
, then the above system is not solvable. Farkas’ lemma asserts that this is in fact the only obstruction:
Farkas’ lemma. Let
be affine-linear functionals. Then exactly one of the following statements holds:
- The system of inequalities
has a solution
.
- There exist non-negative reals
such that
.
As in the previous post, we prove this by induction on d. The trivial case d=0 could be used as the base case, but again it is instructive to look at the d=1 case first before starting the induction.
If d=1, then each inequality can be rescaled into one of three forms:
,
, or
, where
,
, or
is a real number. The latter inequalities are either trivially true or trivially false, and can be discarded in either case. As for the inequalities of the first and second type, they can be solved so long as all of the
which appear here are less than equal to all of the
which appear. If this is not the case, then we have
for some
, which allows us to fashion -1 as a non-negative linear combination of
and
, and the claim follows.
Now suppose that and the claim has already been proven for
. As in the previous post, we now split
for
and
. Each linear inequality
can now be rescaled into one of three forms:
,
, and
.
We fix x’ and ask what properties x’ must obey in order for the above system to be solvable in t. By the one-dimensional analysis, we know that the necessary and sufficient conditions are that for all
, and that
for all
and
. If we can find an x’ obeying these inequalities, then we are in conclusion (1) and we are done. Otherwise, we apply the induction hypothesis and conclude that we can fashion -1 as a non-negative linear combination of the
and of the
. But the
can in turn be expressed as a non-negative linear combination of
and
, and so we are in conclusion (2) as desired.
Exercise: use Farkas’ lemma to derive the duality theorem in linear programming.
— Applications —
Now we connect the above lemma to results which are closer to the Hahn-Banach theorem in its traditional form. We begin with
Separation theorem. Let A, B be disjoint convex polytopes in
. Then there exists an affine-linear functional
such that
for
and
for
.
Proof. We can view the system of inequalities for
and
for
as a system of linear equations on P (or, if you wish, on the coefficients of P). If this system is solvable then we are done, so suppose the system is not solvable. Applying Farkas’ lemma, we conclude that there exists
and
and non-negative constants
such that
for all P. Setting P to be an arbitrary constant, we conclude
and so by the affine nature of P, we can rearrange the above identity as
for all P; since affine functions separate points, we conclude that
.
But by convexity the left-hand side is in A and the right-hand side in B, a contradiction. .
The above theorem asserts that any two disjoint convex polytopes can be separated by a hyperplane. One can establish more generally that any two disjoint convex bodies can be separated by a hyperplane; in particular, this implies that if a convex function always exceeds a concave function, then there is an affine linear function separating the two. From this it is a short step to the Hahn-Banach theorem, at least in the setting of finite-dimensional spaces; if one wants to find a linear functional which has prescribed values on some subspace W, and lies between some convex and concave sets (e.g.
for some semi-norm
), then by quotienting out W we can reduce to the previous problem.
We turn now to the minimax theorem. Consider a zero-sum game between two players, Alice and Bob. Alice can pick any one of strategies using a probability distribution
of her choosing; simultaneously, Bob can pick any one of m strategies using a probability distribution
of his choosing. Alice’s expected payoff F then takes the form
for some fixed real coefficients
; Bob’s expected payoff in this zero-sum game is then
.
Minimax theorem. Given any coefficients
, there exists a unique optimal payoff
such that
- (Alice can expect to win at least
) There exists an optimal strategy
for Alice such that
for all q;- (Bob can expect to lose at most
) There exists an optimal strategy
for Bob such that
for all p.
Proof. By playing Alice’s optimal strategy off against Bob’s, we see that the supremum of the set of which obeys (1) is clearly finite, and less than or equal to the infimum of the set of
which obey (2), which is also finite. To finish the proof, it suffices to show that these two numbers are equal. If they were not equal, then we could find an
for which neither of (1) and (2) were true.
If (1) could not be satisfied, this means that the system of linear equations
has no solution. From the convexity of F(p,q) in q, we can replace this system with
.
Applying Farkas’ lemma, we conclude that some non-negative combination of ,
, and
for
are identically -1. A little bit of algebra shows that there must therefore exist a strategy q for Bob such that -1 can be expressed as a non-negative combination of
,
, and
. In particular,
must be negative for all strategies p for Alice, and so (2) is true, a contradiction.
.
The minimax theorem can be used to give game-theoretic proofs of various theorems of Hahn-Banach type. Here is one example:
Menger’s theorem. Let G be a directed graph, and let v and w be non-adjacent vertices in G. Then the maxflow from v to w in G (the largest number of disjoint paths one can find in G from v to w) is equal to the min-cut (the least number of vertices (other than v or w) one needs to delete from G to disconnect v from w).
The proof we give here is definitely not the shortest proof of Menger’s theorem, but it does illustrate how game-theoretic techniques can be used to prove combinatorial theorems.
Proof. Consider the following game. Bob picks a path from v to w, and Alice picks a vertex (other than v or w). If Bob’s path hits Alice’s vertex, then Alice wins 1 (and Bob wins -1); otherwise Alice wins 0 (and Bob wins 0 as well). Let be Alice’s optimal payoff. Observe that we can prove
by letting Bob picks one of some maximal collection of disjoint paths from v to w at random as his strategy; conversely, we can prove
by letting Alice pick a vertex from some minimal cut set at random as her strategy. To finish the proof we need to show that in fact
and
.
Let’s first show that . Let’s assume that Alice and Bob are both playing optimal strategies, to get the optimal payoff
for Alice. Then it is not hard to use the optimality to show that every path that Bob might play must be hit by Alice with probability exactly
(and any other path will be hit by Alice with probability at least
), and conversely every vertex that Alice might pick will be hit by Bob with probability
(and any other vertex will be hit by Bob with probability at most
).
Now suppose that two of Bob’s paths intersect at some intermediate vertex u. One can show that the two resulting sub-paths from v to u must have an equal chance of being hit by Alice, otherwise by swapping those two sub-paths one can create a path which Alice hits with probability strictly less than , a contradiction. Similarly, the two sub-paths from u to w must have equal chance of being hit by Alice.
Now consider all the vertices u that Alice can pick for which there exists a path of Bob which hits u before it hits any other vertex of Alice. Let U be the set of such u. Every path from v to w must hit U, because if it is possible to avoid U and instead hit another vertex of Alice, it will again be possible to crate a path that Alice hits with probability strictly less than , by the above discussion. Thus, U is a cut set. Any given path of Bob hits exactly one vertex in U (again by the above discussion). Since each u in U has a probability
of being hit by Bob, we thus see that this cut set has size exactly
. Thus
as desired.
Now we show that . Define an
-flow to be a collection of non-negative weights on the directed edges of G such that
- the net flow at v (the total inflow minus total outflow) is -1, and the net flow at w is +1;
- for any other vertex u, the net flow at u is zero, and total inflow or outflow at u is at most
.
We first observe that at least one -flow exists. Indeed, if we pick one of Bob’s optimal strategies, and weight each edge by the probability that Bob’s path passes through that edge, one easily verifies that this gives a
-flow.
Given an -flow, consider the directed graph G consisting of directed edges on which the weight of the
-flow is strictly between 0 and
. Observe that if an edge in G terminates at a vertex with net inflow less than
, then there must be a edge in G exiting this vertex also; conversely, if an edge in G terminates at a vertex with net inflow at least
, then there must be another edge in G coming into this vertex also. Similarly, if an edge in G originates in a vertex with net outflow less than
, there must be an edge in G entering this vertex; and if it originates in a vertex with net outflow at least
, then there must be another edge in G exiting this vertex. Thus, if G is not empty, then one can chase an edge backwards and forwards and end up with a simple oriented cycle consisting of edges in G and reversals of edges in G, such that at any vertex with net inflow at least
, every edge in G entering this vertex in the cycle is immediately followed by a reversed edge in G exiting the vertex, and similarly at any vertex with net outflow at least
, every reversed edge in G entering the vertex is immediately followed by an edge in G exiting the vertex. Given such a cycle, then one can modify the
-flow on this cycle by an epsilon, increasing the flow weight by
on edges on the cycle that go with the flow, and reducing them by the same
on edges that go against the flow; note that this preserves the property of being an
-flow. Increasing
, we eventually reduce one of the weights to zero, thus reducing the number of edges on which the flow is supported. We can repeat this procedure indefinitely until one arrives at an
-flow whose graph G is empty, thus every edge has weight either zero or
. Now, as v has outflow at least +1 and every vertex adjacent to v can have inflow at most
(recall that v is not adjacent to w), the flow must propagate from v to at least
other vertices. Each of these vertices must eventually flow to w (which is the only vertex with positive flow) by at least one path; by the above discussion, these paths need to be disjoint. Thus we have
as desired.
.
The above argument can also be generalised to prove the max-flow min-cut theorem, but we will not do so here.
Exercise: use Menger’s theorem to prove Hall’s marriage theorem.
Now we turn to Helly’s theorem. One formulation of this theorem is the following:
Helly’s theorem. Let
be a collection of convex bodies in
with
. If every d+1 of these convex bodies have a point in common, then all m of these convex bodies have a point in common.
The reader is invited to verify Helly’s theorem in the case, to get a flavour as to what is going on.
For simplicity we shall just consider the case when each of the are convex polytopes.
Proof. A convex polytope is the intersection of finitely many half-spaces. From this, one quickly sees that to prove Helly’s theorem for convex polytopes, it suffices to do so for half-spaces. Each half-space can be expressed as the form for some linear functional
and
. Note that by duality, one can view
as living in an d+1-dimensional vector space
.
Let say that there are m half-spaces involved, and let be the corresponding linear functionals. It suffices to show that if the system
has no solution, then there is some sub-collection
with
such that
also has no solution.
By Farkas’ lemma, we know that the system has no solution if and only if (0,-1) is a convex combination of the
. So everything reduces to establishing
Dual Helly theorem. Suppose that a vector v in a d+1-dimensional space can be expressed as a non-negative linear combination of a collection of vectors
. Then v is also a non-negative combination of at most d+1 vectors from that collection.
To prove this theorem, we use an argument a little reminiscent to that used to prove in the proof of Menger’s theorem. Suppose we can express v as a convex combination of some of the
. If at most d+1 of the vectors have non-zero coefficients attached to them then we are done. Now suppose instead that at least
vectors have non-zero coefficients, say
have non-zero coefficients. Then there is a linear dependency among these vectors, which allows us to find coefficients
, not all zero, such that
. We can then perturb our preceding non-negative combination by an epsilon multiple of this equation to obtain a new representation of 0 as a non-negative combination of vectors. If we increase epsilon, we must eventually send one of the coefficients to zero, decreasing the total number of vectors with non-zero coefficients. Iterating this procedure we eventually obtain the dual Helly theorem and hence the original version of Helly’s theorem.
[Update, Apr 30: Proof of Helly’s theorem fixed.]

27 comments
Comments feed for this article
1 December, 2007 at 3:58 am
Francois
Thank you for this expository note.
You might be interested in the following discrete variant of Farkas’ Lemma, where inequalities of the type “ ” are replaced by “is an integer”:
” are replaced by “is an integer”:
Let a full row-rank integer matrix and
a full row-rank integer matrix and 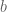 an integer vector.
an integer vector.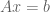 and
and  is an integer vector
is an integer vector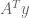 is an integer vector and
is an integer vector and 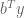 is not integer
is not integer
Exactly one of the following two systems has solutions:
1.
2.
(the continuous Farkas Lemma you described being equivalent to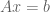 and
and  is
is 
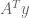 is
is  and
and 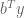 is not
is not  )
)
Exactly one of the following two systems has solutions:
1.
2.
I wonder to which other sets (besides and
and 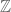 this can be generalized.
this can be generalized.
2 December, 2007 at 11:17 am
Anonymous
a doubt about the induction in the proof of hahn-banach:
you had written:
“If we can find an x’ obeying these inequalities, then we are in conclusion (1) and we are done. Otherwise, we apply the induction hypothesis and conclude that we can fashion -1 as a non-negative linear combination of the c_j(x’) and of the b_k(x’) – a_j(x’). But the b_k(x’) – a_j(x’) can in turn be expressed as a non-negative linear combination of t – a_j(x’) and b_k(x’)-t, and so we are in conclusion (2) as desired.”
But in the application of the induction hypothesis, each x’ may use a different linear combination of the c_j(x’) and b_k(x’)- a_j(x’) to get -1. what we want
is a linear combination of the formal linear polynomials c_j(X) and b_k(X) -a_j(X) to get -1 as formal linear polynomials (where X is an indeterminate).
Is this right?
3 December, 2007 at 8:30 pm
Terence Tao
Dear Francois: Thank you for pointing out the integer version of the Farkas lemma, which I was not aware of. It seems like one could adapt the proof in my post (i.e. induct on dimension, using a careful analysis of the one-dimensional case) to establish this version also, although the one-dimensional analysis is somewhat different (in particular, it seems to use the Chinese remainder theorem). I don’t know how general the phenomenon is, but one obvious thing to do is to replace the integers by other integral domains, e.g. the ring of terminating base p decimals for some fixed p.
Dear Anonymous: We only apply the induction hypothesis once. If we are not in the first case (in which there exists at least one x’ obeying the inequalities and
and  ), then there do not exist any x’ which obey these inequalities. The induction hypothesis then asserts that there must be a single non-negative linear combination of the affine-linear forms
), then there do not exist any x’ which obey these inequalities. The induction hypothesis then asserts that there must be a single non-negative linear combination of the affine-linear forms 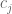 and
and  which sum to -1 (for any value of x’).
which sum to -1 (for any value of x’).
4 December, 2007 at 10:20 pm
Matthias Aschenbrenner
Generalizations of Farkas’ Lemma to other kinds of systems of (in-) equalities have been recently considered by Philip Scowcroft, Nonnegative solvability of linear equations in certain ordered rings, Trans. Amer. Math. Soc. 358 (2006), no. 8, 3535–3570, MR2218988 (2007k:03102). For example, he gives a Farkas-type condition of the existence of a non-negative integer solution x\in N^n to a system Ax=b where A, b have integer entries; also, for solutions in dense subrings of the reals, etc.
The equivalence between an existential statement (“there exists a solution …”) and a universal statement (“for all non-negative reals …”) as in your statement of Farkas’ Lemma hints, for a model-theorist, at the presence of a general quantifier-elimination result lurking in the background. (In this case, this is the quantifier elimination for the theory of ordered R-linear spaces, a.k.a. “extended Fourier-Motzkin elimination”.)
The integer version of Farkas’ Lemma mentioned by Francois is due to Kronecker (1884). One can also prove a “mixed real-integer” version by requiring only some of the coordinates in the solution to be integer. (Again, this can be deduced from a more general elimination result.)
6 December, 2007 at 12:13 am
Terence Tao
Dear Matthias,
Thanks for the references (and a belated welcome to UCLA)!
30 April, 2008 at 9:49 am
Arseny Akopyan
Dear Terry,
I do not understand the proof of the Helly theorem. Why may we suppose that half-spaces do not contain the origin? Say, if two of them are {x_n>-1} and {x_n<1}, then any point is contained in at least one of these two.
30 April, 2008 at 10:15 am
Terence Tao
Hmm, you’re right; one can’t normalise all the coefficients to equal 1. Fortunately, the proof can be modified to handle this case; I’ve made the appropriate corrections. (And I should adjust the version in the book as well…)
16 August, 2008 at 12:22 am
Sune Kristian Jakobsen
“Now we show that ” Don’t you mean
” Don’t you mean  ?
?
16 August, 2008 at 11:53 am
Terence Tao
Dear Sune: Thanks for the correction!
3 October, 2008 at 11:41 am
The Anonymous
Does anybody know of a simple, “pivoting-type” algorithm allowing one to determine whether the system of linear inequalities has a solution? Of course, one can reduce this system to one which is considered standard, but this requires more variables and inequalities to be brought into consideration; besides, the above system looks simpler and more appealing than the “standard” one, hence one can expect a nicer algorithm for handing it to exist.
has a solution? Of course, one can reduce this system to one which is considered standard, but this requires more variables and inequalities to be brought into consideration; besides, the above system looks simpler and more appealing than the “standard” one, hence one can expect a nicer algorithm for handing it to exist.
26 January, 2009 at 6:28 pm
245B, Notes 6: Duality and the Hahn-Banach theorem « What’s new
[…] of variants of the Hahn-Banach theorem (in the finite-dimensional setting) can be found at this blog post of mine. Possibly related posts: (automatically generated)Dual SpacesBasic Theory of Banach […]
30 May, 2009 at 1:54 pm
Structure and Randomness: Pages from Year One of a Mathematical Blog « Abner’s Postgraduate Days
[…] The Hahn-Banach theorem, Menger’s theorem, and Helly’s theorem The Hahn-Banach theorem is a theorem in mathematical analysis. The definition on wikipedia is too abstract for me to image what the usage of this ‘tool’ is, however, this article in fact discuss the famous lemma — Farkas’ lemma which is sometimes known as Hahn-Banach theorem. (T. Tao said that) Farkas’ lemma. Let be affine-linear functionals. Then exactly one of the following statements holds: […]
7 June, 2009 at 1:01 pm
Predavanje RAG.4 → (poglavje 1) « igor’s math Blog
[…] lema, separacija konveksnih množic, Hilbertov Nullstellensatz. Izhodišče tega razdelka je bil prispevek T. Tao (UCLA), kjer je predstavil zanimiv dokaz Farkaseve leme s pomočjo indukcije. Na […]
5 June, 2010 at 12:58 pm
254B, Lecture Notes 7: The transference principle, and linear equations in primes « What’s new
[…] theorem is applicable. (One could also use closely related results, such as the Farkas lemma: see this earlier blog post for more discussion.) Indeed, suppose that there was some for which and were disjoint. Then, by […]
26 June, 2010 at 9:28 am
The uncertainty principle « What’s new
[…] Convex duality More generally, a (closed, bounded) convex body in a vector space can be described either by listing a set of (extreme) points whose convex hull is , or else by listing a set of (irreducible) linear inequalities that cut out . The fundamental connection between the two is given by the Farkas lemma. […]
22 November, 2011 at 6:59 am
Jay
Dear Terence!
Could you please elaborate a little more on the proof of Helly’s theorem. Unfortunately for me it wasn’t obvious what’s the dual problem? According to the definition of Linear Programming, which objective function should be used? And please, few more words as conclusion why exactly the theorem is right.
Thanks!
13 November, 2012 at 3:28 pm
Alexander Shamov
Dear Prof. Tao,
It seems that in your proof of Farkas’ lemma we obtain a linear combination for every fixed , so that
, so that 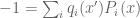 , where
, where 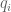 ‘s depend on
‘s depend on  in a way that we do not control, whereas we want them to be constant…
in a way that we do not control, whereas we want them to be constant…
13 November, 2012 at 5:09 pm
Terence Tao
When we apply the induction hypothesis to the system ,
,  , the coefficients
, the coefficients 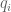 generated by conclusion 2 of Farkas’s lemma applied in dimension d-1 do not depend on the underlying variables
generated by conclusion 2 of Farkas’s lemma applied in dimension d-1 do not depend on the underlying variables 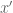 .
.
13 November, 2012 at 5:18 pm
Alexander Shamov
Ah, I see, thank you.
13 November, 2012 at 6:13 pm
HUMBERTO
ES INTERESANTE LA FORMA COMO SE INTERACTUA CON EL CONOCIMIENTO Y SOBRE TODO EN ESTE CAMPO DE LA MATEMÁTICAS
MI PREGUNTA ES
¿ SE RESTRINGE ESTE TIPO DE ANÁLISIS O EXTENSIÓN EN LA TEORÍA DE REPRESENTACIÓN DE CONJUNTOS PARCIALMENTE ORDENADOS EN EL CASO DE POSET CRÍTICOS ( KLEINER O NAZAROVA) O SE GENERA UN PUENTE NETAMENTE ALGEBRAICO?
18 February, 2015 at 1:51 pm
254A, Notes 4: Some sieve theory | What's new
[…] theorem; one can also proceed using one of the other duality results mentioned above. (See this previous blog post for some discussion of the connections between these various forms of linear duality.) Consider the […]
21 February, 2018 at 10:33 pm
John Baez
“Alice can pick any one of $n$ strategies.”
You need one of those darn “latex” commands here.
[Corrected, thanks – T.]
24 March, 2019 at 8:20 am
George Shakan
I am curious what intuitive crutches you use for thinking of high dimensional problems involving convexity. You do have a nice post on math overflow outlining some ideas for thinking in high dimensions in general..but the only example from that post that I can see to have a natural interpretation in terms of convexity is the two-player game.
25 March, 2019 at 1:46 pm
Terence Tao
I’ve actually asked other people (such as Keith Ball) about this, since I do not have much native experience with high-dimensional convex bodies. But the viewpoint of Vitali Milman that was pointed out by Gil Kalai in the same math overflow post ( https://mathoverflow.net/a/26010/766 ) is, I think, a good one: convex bodies in high dimensions are largely ellipsoidal but also can contain a number of “spikes” that are small in volume but which can protrude well beyond the main ellipsoid of the convex body. Foundational results in high dimensional convex geometry such as Dvoretsky’s theorem, the Bourgain-Tzafriri theorem, or the Johnson-Lindenstrauss lemma are broadly in line with this intuitive picture. (For low dimensions one has instead John’s ellipsoid theorem, which basically says that one just has the ellipsoid and no spikes.)
7 November, 2020 at 4:37 am
Peter Bob
“Then it is not hard to use the optimality to show that every path that Bob might play must be hit by Alice with probability exactly \alpha”
Would anybody be able to give a hint as to why this is true?
8 November, 2020 at 9:58 pm
Terence Tao
Oops, there was a typo in this paragraph; it is assumed that Alice and Bob are both playing optimal strategies (not just Alice). Since Alice is guaranteed a payoff of no matter what strategy Bob plays, every possible path has to be hit with probability at least
no matter what strategy Bob plays, every possible path has to be hit with probability at least  ; but the optimal strategy that Bob actually is playing gives a payoff of exactly
; but the optimal strategy that Bob actually is playing gives a payoff of exactly  , so all the paths that Bob uses also has to be hit with probability exactly
, so all the paths that Bob uses also has to be hit with probability exactly  (otherwise if one of these paths was hit with a larger probability, the payoff would be strictly larger than
(otherwise if one of these paths was hit with a larger probability, the payoff would be strictly larger than  ).
).
10 November, 2020 at 1:40 am
Anonymous
I see. Thank you very much for the answers and the exposition. The game-theoretic proof of Menger’s theorem is fascinating.