It’s now been almost a year since I moved my “What’s new?” page from my home page to this blog. Since then, I’ve been quite happy with the directions this blog has been headed in (most of which I had not anticipated when I started), and also with the level of feedback, some of which has been extremely informative to me (and, I hope, to other readers as well).
Anyway, after discussing things with some of my friends and colleagues, I have decided to convert some of the posts here from 2007 into a book format, in order to place some of the mathematical content here in a more formal and traditional context (with accurate citations and references, etc.). After some thought, I decided not to transcribe all of my posts from last year (there are 93 of them!), but instead to restrict attention to those articles which (a) have significant mathematical content, (b) are not announcements of material that will be published elsewhere, and (c) are not primarily based on a talk given by someone else. As it turns out, this still leaves about 33 articles from 2007, leading to a decent-sized book of a couple hundred pages in length. For various reasons (including legal reasons), I have decided not to incorporate the comments to each post directly into the book format, although corrections, mention of relevant references, etc. will be added with acknowledgments in the endnotes to each article.
I’ve converted a couple articles into a book format, and also created a table of contents, to see what it would look like. (The format comes from the American Mathematical Society, with whom I am planning to publish the book.) It looks like it will be relatively straightforward to convert the rest (at least compared to writing books from scratch, which I know from experience to be quite time-consuming!). I’ll of course post updates here on this blog when the book is closer to completion.
At present, the structure and content of the book is still rather flexible; like all things related to this blog, it is an experiment. As such, I am open to suggestions on these matters. (For instance, I do not have any particularly imaginative title for the book, other than “What’s new – 2007”. )
What's new 
25 comments
Comments feed for this article
25 January, 2008 at 10:02 pm
KenF
Everyone wants you to release the book under a creative commons license.
25 January, 2008 at 11:43 pm
Derek Buchanan
Perhaps a better title would be
What was new in 2007
because what was new in 2007 isn’t new in 2008!
26 January, 2008 at 12:21 am
Tom
Dear Prof. Tao,
that’s a very nice idea, and I would too suggest using a CC licence (or at least have an online copy available for private use, like Allen Hatcher’s topology book).
Also do you have a way of regularly archiving the whole blog content including comments (just in case the wordpress servers break down, it would be a huge loss!).
For the title I’d suggest to add an informative subtitle, and to think about it from a long-term perspective. For instance will there be such a book every year? If so will the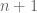
book always systematically report on any significant advances made on the open problems presented in years 
to 
even if it is not the subject of a post of yours in year 
? And so forth.
26 January, 2008 at 1:32 am
Attila Smith
Youpi!
which is French for
“What an excellent piece of news. I’m looking forward to buying this book
and devouring it, comfortably sitting in my best armchair, sipping cup after cup of moka coffee, Brahms gently played in the background ”
(French is a very concise language.)
26 January, 2008 at 4:44 am
Przemyslaw Chojecki
Superb idea. Would be also wonderful to see in the future an ongoing course in Dynamical Systems of yours in a book format, enriched maybe with solutions of some of exercises. Is it a chance for it?
Best Regards
26 January, 2008 at 11:42 am
DeadWolfe
I second the idea of making the dynamical systems notes into a book.
26 January, 2008 at 5:07 pm
km
Hi,
Will the book be sold in bookstores?
KM
26 January, 2008 at 6:15 pm
Anonymous
Good job!I think the many will appreciate your work.
26 January, 2008 at 7:24 pm
Terence Tao
Dear all: thanks for the suggestions so far!
A subtitle does indeed resolve my concerns about the title being somewhat obscure (and, as one commenter pointed out, somewhat anachronistic).
I have not planned far ahead enough to see what to do about the (as yet mostly non-existent) 2008 posts, including the 254A lecture series notes, but presumably if the conversion of the 2007 posts proceeds painlessly and successfully then I will be encouraged to repeat the process in the future (though perhaps not exactly on an annual basis, depending on how the blog evolves; the idea of publishing one book a year, on top of all my other duties, does seem slightly excessive).
The reminder to backup this blog is also a good suggestion, and one which I will now do on a regular basis. [It turns out that it was just a matter of clicking a button from a menu; see
http://faq.wordpress.com/2005/09/28/backups/
. I now have a 981KB XML file which seems to contain all the essential content of the blog as of today.]
Judging by how my other books have been faring (with the possible exception of my problem solving book), I would doubt that you would see this book physically in a store, but with the magic of on-line retailing I would imagine that availability is unlikely to be a concern (as with other books published by the AMS). In any case, the original blog posts that the book is going to be almost entirely based on will be available at this site.
I am not an expert in licensing issues, but it seems that the usual academic model (in which the content of one’s publications can be used freely by later authors, with proper citation and attribution of course) would suffice here. (As said above, I am restricting the book to my own content, as opposed to that generated from the comments or from colleagues; the book will be based on the blog, but will not be an exact replica of it.)
27 January, 2008 at 6:45 am
Isabel Lugo
I hope that this book will include the “career advice” posts, which I have found very useful in understanding how at least one “real mathematician” perceives mathematics. (I’m not sure if you consider them part of the blog proper, which is why I’m making this comment.)
Or, at the very least, I hope that more people read those posts. Such writings — by you and by other mathematicians — have made my transition from a student to a researcher (which is still in progress) easier to handle. The book venue may not be the right place for that, since it’s not obvious who exactly the market for the book is, and it may or may not include beginning graduate students, who are the ones who I’d think would benefit from such advice.
27 January, 2008 at 8:37 am
Harald Helfgott
(I do not know whether this belongs here or on the original entry on the non-commutative Freiman theorem, which I did not read at the time; feel free to move it, if necessary.)
You say that the growth of subsets of G=SL_2(F_p) which do *not* generate A has not been studied. As it happens, any subset of G that does not generate A is either in a dihedral group or in a Borel subgroup. It should take about two seconds to deduce a Freiman theorem for a dihedral group from the Freiman theorem over Z/nZ.
The case of subsets of a Borel is more interesting. I think I told you (on this blog) some time ago that the “right” formulation of the sum-product theorem is not over fields – or, rather, the sum-product theorem is a “shadow” of a more general result about groups with commuting automorphisms. That same general result has an even more direct application to Borel subgroups. You see, the maximal torus T (the set of diagonal matrices, say) in a Borel subgroup B (the set of upper triangular matrices) acts by conjugation on the nilpotent subgroup U consisting of the unipotent elements of B (the set of upper triangular matrices). The actions commute because T is abelian.
(I am leaving out an important technical condition that is fulfilled trivially for SL_2 (as opposed to SL_n).)
The consequence is that, if a subset A of a Borel contains at least M diagonal elements and at least one unipotent element other than the identity, it will grow by a factor of at least M^{epsilon}, unless almost all the unipotents are already in the set. One can get plenty of diagonal elements by the same method I used in my SL_2 paper – unless A lies in a very small number of cosets of the unipotents.
There are plenty of little corners left over, as you can see. Would you think it worthwhile to write the complete “non-commutative Freiman theorem” for SL_2 down in its entirety? Do you know whether somebody is already doing that? I may be getting a graduate student soon, and this might be a nice warm-up problem; I do not know what you think.
In general, I’d expect something much like Freiman’s theorem for unipotent groups; I would guess growth is forced for subsets of non-solvable groups that do not lie in a solvable subgroup; and, finally, I’d expect growth in solvable groups to be
described by a mildly complicated version of Freiman’s theorem when the
set of eigenvalues of elements of the set A is small, and to be forced otherwise. It seems clear to me that the second task is the hardest (given that we already know Freiman over abelian groups). Even the third task might not be hard.
Tell me if there is something you know that does not fit in this division.
27 January, 2008 at 10:58 am
Terence Tao
Dear Harald,
It would certainly be of interest for someone (such as your student) to write up a complete non-commutative Freiman theorem for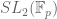
; I do not know of anyone who is already doing this. Besides the issue of subgroups, there is also the issue of what happens for very dense sets A (of size 
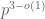). Presumably what happens here is that iterated products of A soon fill up all of 
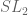, because of the lack of low-dimensional representations (i.e. quasirandomness). In any case, sorting all this out would be an excellent data point with which to test various candidates for the conjectured “non-commutative Freiman theorem”, at least for nice classical groups such as 
.
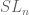Dear Isabel: Thanks for the suggestion. At this point it will depend to some extent on how much space everything else is going to take up. The case for making a print version of the career advice pages is a little less compelling to me than for the mathematically oriented pages, since the the latter is likely to continue to evolve slowly over time and is not really in need of a stable (and citeable) version. So I may save it for a future lean year in the blog if there is not enough other material to make a decent book.
Incidentally, I doubt that I will keep issuing updates to articles from year n in a book for year n+m; this is the kind of thing which is much better done in the online blog format than in the static book format.
28 January, 2008 at 2:48 am
Harald Helfgott
Dear Terry,
Gowers worked out (in effect) what happens for very dense sets A: as pointed out by Nikolov and Pyber, the result in his paper on Quasirandom Groups has the very nice consequence that, when |A|>p^{2.5+epsilon} or so, A*A*A is the entire group SL_2(F_p).
From a talk by Babai, I know that Babai, Nikolov and Pyber now have a beautiful and completely general result. They work out that A*A*A is in fact equal to G for sufficiently large subsets of G, where G is any group that lacks low-dimensional representations. Here “sufficiently large” is tight. Moreover, they give bounds on the number of copies of A that are needed to cover G for softer senses of “sufficiently large”.
28 January, 2008 at 8:11 am
Max
Dear Terry,
I would also like to hear your opinion on publishing the book under CC license and why do you have this opinion.
Thanks. :)
28 January, 2008 at 8:13 am
Max
Oops sorry, I didn’t notice that you’ve already answered to this question.
29 January, 2008 at 3:29 pm
Roberta
Congratulations!!
“Why global regularity for Navier-Stokes is hard” and “The parity problem in sieve theory” are my favourite ones.
But why not “Einstein’s derivation of E=mc^2”? I really like this post. ( (a) restriction? =P)
30 January, 2008 at 8:41 pm
Terence Tao
Dear Roberta,
I drafted the contents list before the Einstein post (the last post of 2007!). But thanks for reminding me to put it in. I hope to put an updated version of the book here in a few weeks.
31 January, 2008 at 6:46 am
Technoliterati « ,Never Neutral,
[…] Just recently, my friend Pablo left a comment on this blog with a link to mathematician’s Terence Tao’s blog, where he explains the process of making a book out of his blog posts. A professor of the […]
11 February, 2008 at 8:50 pm
t8m8r
If it is not secret what efficient method are you thinking of to convert the blog-formatted files to tex format?
13 February, 2008 at 7:36 am
Terence Tao
Dear t8m8r,
I am mostly relying on plain old search-and-replace, which takes care of a lot of the conversion, but of course many finer details (particularly in converting links to references) have to be taken care of by hand (and I want to go through the material carefully in any case).
13 February, 2008 at 10:13 am
t8m8r
Thanks a lot. I am just starting a blog and thought it would be nice to have tex-version of some of the posts. At the same time I was a bit lazy to convert by hand. Your answer “in any case I want to go through the material carefully” kind of settles the issue for me too.
27 February, 2008 at 6:37 am
Using MathTran in blogs and wikis « Jonathan Fine’s weblog
[…] In fact, let’s start with Terry Tao’s blog, which is on WordPress. In case you didn’t know, Terry Tao is an eminent and talented young mathematician who is extremely web-savvy. He decided to move from a static web-site to a blog for his news and discussion articles about a year ago. Original he moved to blogspot, but then soon moved on to WordPress, because it gave better LaTeX support. Last month he told us that he has decided to publish a book version of his blog. […]
19 April, 2008 at 2:23 pm
A draft version of the blog book « What’s new
[…] April, 2008 in book, non-technical, update A few months ago, I announced that I was going to convert a significant fraction of my 2007 blog posts into book format. For […]
7 December, 2010 at 5:14 am
Writing & Blogging | neverendingbooks
[…] Tao is reworking some of his better blogposts into a book, to be published by the AMS (here’s a preliminary […]
2 September, 2011 at 2:48 am
On Blogging and ‘Technoliterati’ | Networked Researcher
[…] Just recently, my friend Pablo left a comment on this blog with a link to mathematician’s Terence Tao’s blog, where he explains the process of making a book out of his blog posts. A professor of the […]