I’ve uploaded a new paper to the arXiv entitled “The sum-product phenomenon in arbitrary rings“, and submitted to Contributions to Discrete Mathematics. The sum-product phenomenon asserts, very roughly speaking, that given a finite non-empty set A in a ring R, then either the sum set or the product set
will be significantly larger than A, unless A is somehow very close to being a subring of R, or if A is highly degenerate (for instance, containing a lot of zero divisors). For instance, in the case of the integers
, which has no non-trivial finite subrings, a long-standing conjecture of Erdös and Szemerédi asserts that
for every finite non-empty
and every
. (The current best result on this problem is a very recent result of Solymosi, who shows that the conjecture holds for any
greater than 2/3.) In recent years, many other special rings have been studied intensively, most notably finite fields and cyclic groups, but also the complex numbers, quaternions, and other division algebras, and continuous counterparts in which A is now (for instance) a collection of intervals on the real line. I will not try to summarise all the work on sum-product estimates and their applications (which range from number theory to graph theory to ergodic theory to computer science) here, but I discuss this in the introduction to my paper, which has over 50 references to this literature (and I am probably still missing out on a few).
I was recently asked the question as to what could be said about the sum-product phenomenon in an arbitrary ring R, which need not be commutative or contain a multiplicative identity. Once one makes some assumptions to avoid the degenerate case when A (or related sets, such as A-A) are full of zero-divisors, it turns out that there is in fact quite a bit one can say, using only elementary methods from additive combinatorics (in particular, the Plünnecke-Ruzsa sum set theory). Roughly speaking, the main results of the paper assert that in an arbitrary ring, a set A which is non-degenerate and has small sum set and product set must be mostly contained inside a subring of R of comparable size to A, or a dilate of such a subring, though in the absence of invertible elements one sometimes has to enlarge the ambient ring R slightly before one can find the subring. At the end of the paper I specialise these results to specific rings, such as division algebras or products of division algebras, cyclic groups, or finite-dimensional algebras over fields. Generally speaking, the methods here give very good results when the set of zero divisors is sparse and easily describable, but poor results otherwise. (In particular, the sum-product theory in cyclic groups, as worked out by Bourgain and coauthors, is only recovered for groups which are the product of a bounded number of primes; the case of cyclic groups whose order has many factors seems to require a more multi-scale analysis which I did not attempt to perform in this paper.)
The key strategy is to study sets of the form
for various (which will usually be a non-zero-divisor), and some suitable threshold parameter M (which will be a little bit larger than the sum and product doubling constants of A). Roughly speaking,
collects all the dilates
of A which are “parallel” to the dilate
in an additive sense. There is a remarkable “self-improving property” of these sets which shows, under suitable hypotheses on A, a, and M, that every element x of
in fact obeys the improved estimate
for some M’ that can be arranged to be significantly smaller than M. In other words, there is a gap phenomenon: the quantity
can be very small or very large, but cannot be of intermediate size. This gap then leads to some very strong algebraic control on the
; for instance, under reasonable assumptions,
becomes an additive group, and also exhibits good multiplicative closure properties (for instance,
will be a subring). Once one has all this algebraic structure, the proofs of the theorems are then a relatively routine application of the sum-set theory and some elementary algebra.
There is still the issue of what to do when there are plenty of zero divisors. I don’t have a satisfactory resolution to this problem in general, but in the case of finite dimensional algebras over a field, in which the set of zero divisors forms an algebraic set, one can use some basic algebraic geometry to show that if a set of small additive doubling is concentrating inside the set of zero divisors, then it must in fact concentrate inside an affine subspace contained in the set of zero divisors. This does not fully determine the structure of such a set, but it seems to be a useful first step towards analysing this case further.
[See also my third Milliman lecture “Sum-product estimates, expanders, and exponential sums“.]

12 comments
Comments feed for this article
18 June, 2008 at 6:31 am
some_student
Dear Terry, this is interesting, do you know if similar robustness questions have been investigated for other structures than addition and multiplication? For instance if one were to consider the “tropical” operations and
and 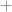 ? Or if one looked at a set equiped with one binary law (like
? Or if one looked at a set equiped with one binary law (like 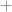 or
or  ) and one higher order law (e.g. a ternary operation that is not defined in tems of addition and multiplication)?
) and one higher order law (e.g. a ternary operation that is not defined in tems of addition and multiplication)?
18 June, 2008 at 7:30 am
Terence Tao
Dear some_student,
There is some work by Igor Shparlinski on an exponential version of sum-product in finite fields, where one looks at the sets {g^a+g^b: a in A, b in B} and {g^{ab}: a in A, b in B} for some generator g, and also on elliptic curve versions in which one looks at { x(aP) + x(bP): a in A, b in B} and {x(abP): a in A, b in B}, where P is a point on an elliptic curve of some order p, A and B are sets in F_p, and x is the x coordinate of the elliptic curve. Presumably there are many further variations on these themes.
One particularly nice problem, by the way, is to work out all the polynomials P(x,y) of two variables for which P(A,A) is necessarily much larger than A whenever A is a finite set of, say, integers with A+A small. Apart from trivial examples such as functions of a linear polynomial in x and y, it should be that one has a result of the form |P(A,A)| \geq |A|^{1+c} for any such P, where c depends on P. There is some work by Van Vu in this direction at
http://arxiv.org/abs/0705.0715
In the tropical setting, there is unlikely to be any phenomenon of this type, because of the degeneracy of the min operation: the min-set of A and A is just A, and so the min-sum problem is really just a sum problem.
22 June, 2008 at 11:33 pm
Adelaide Boy
Dear Terry,
Along with a recent Anonymous, I often read your posts without
understanding the details. I have been able to follow this paper
because you kept it elementary, and thankyou for that.
In your proof of 3.1.(i), you seem to assume that dA-AA is a subset
of AA-AA. However, d \in A-A, so dA-AA would be a
subset of AA-2AA. Is that right? Also, r and b seem to be
the same variable in this section.
Adelaide Boy
23 June, 2008 at 8:31 am
Terence Tao
Dear Adelaide Boy: Thanks for the corrections!
9 July, 2008 at 5:18 pm
Begging for Submissions « Rigorous Trivialities
[…] The sum-product phenomenon in arbitrary rings […]
13 July, 2008 at 4:01 am
John R Ramsden
I wonder if a related type of phenomenon, perhaps a special case, is at work with the Mahler measure of polynomials, which Graeme Taylor blogged about a few months ago at http://maths.straylight.co.uk/archives/114
Quoting from his article:
10 September, 2008 at 1:45 pm
another student
Dear Terry, is there any reason this specific conjecture is of interest? What would be its implications in the research in additive number theory?
10 September, 2008 at 7:51 pm
Terence Tao
Dear another student:
While the Erdos-Szemeredi conjecture, if true, might possibly have some direct application to number theory (it is tempting, for instance, to try to apply it to, say, the set of quadratic residues in an interval to learn something about their distribution), I would imagine that the new techniques, ideas, and insights that would go into any future proof of this conjecture may be even more interesting, in many ways, than the result itself. (A lot of problems in combinatorics or analysis are of this nature; they can be viewed as sort of benchmarks for measuring the technological progress of one’s tools.)
22 November, 2008 at 8:46 am
Marker lecture IV: “Sieving for almost primes and expanders” « What’s new
[…] are now some quite elementary proofs of this theorem, but I will not discuss them here (see e.g. my earlier blog post on this topic). I should note, though, that the bulk of the Bourgain-Gamburd-Sarnak work is preoccupied with […]
27 August, 2010 at 4:01 am
Xavier
Dear Terry, sorry for digging out this old thread.
Did you already consider non-associative rings ?
Those arising from octonion algebras, whose multiplication
verifies the Moufang identities: (ab)(ca)=(a(bc))a
There are some similarities between SL2(Z) (split-quaternions of norm 1)
and Zorn “Vektormatrix” (split-octonions). It would then be great to have an equivalent of Helfgott’s results concerning SL2(Z) for Vektormatrices over Z.
27 August, 2010 at 9:08 am
Terence Tao
I did not consider non-associative rings, and the arguments in my paper certainly rely on associativity in a number of places. To my knowledge, there is no literature on the sum-product question for octonions, though I can imagine that such a result is potentially within reach of the current technology.
5 February, 2012 at 11:33 am
254B, Notes 5: Product theorems, pivot arguments, and the Larsen-Pink non-concentration inequality « What’s new
[…] exponent in the sum-product theorem. A relatively recent survey of this literature can be found in this paper of mine. In , the best result currently in this direction is by Solymosi, who established that one can take […]