A dynamical system is a space X, together with an action of some group
. [In practice, one often places topological or measure-theoretic structure on X or G, but this will not be relevant for the current discussion. In most applications, G is an abelian (additive) group such as the integers
or the reals
, but I prefer to use multiplicative notation here.] A useful notion in the subject is that of an (abelian) cocycle; this is a function
taking values in an abelian group
that obeys the cocycle equation
(1)
for all and
. [Again, if one is placing topological or measure-theoretic structure on the system, one would want
to be continuous or measurable, but we will ignore these issues.] The significance of cocycles in the subject is that they allow one to construct (abelian) extensions or skew products
of the original dynamical system X, defined as the Cartesian product
with the group action
. (The cocycle equation (1) is needed to ensure that one indeed has a group action, and in particular that
.) This turns out to be a useful means to build complex dynamical systems out of simpler ones. (For instance, one can build nilsystems by starting with a point and taking a finite number of abelian extensions of that point by a certain type of cocycle.)
A special type of cocycle is a coboundary; this is a cocycle that takes the form
for some function
. (Note that the cocycle equation (1) is automaticaly satisfied if
is of this form.) An extension
of a dynamical system by a coboundary
can be conjugated to the trivial extension
by the change of variables
.
While every coboundary is a cocycle, the converse is not always true. (For instance, if X is a point, the only coboundary is the zero function, whereas a cocycle is essentially the same thing as a homomorphism from G to U, so in many cases there will be more cocycles than coboundaries. For a contrasting example, if X and G are finite (for simplicity) and G acts freely on X, it is not difficult to see that every cocycle is a coboundary.) One can measure the extent to which this converse fails by introducing the first cohomology group , where
is the space of cocycles
and
is the space of coboundaries (note that both spaces are abelian groups). In my forthcoming paper with Vitaly Bergelson and Tamar Ziegler on the ergodic inverse Gowers conjecture (which should be available shortly), we make substantial use of some basic facts about this cohomology group (in the category of measure-preserving systems) that were established in a paper of Host and Kra.
The above terminology of cocycles, coboundaries, and cohomology groups of course comes from the theory of cohomology in algebraic topology. Comparing the formal definitions of cohomology groups in that theory with the ones given above, there is certainly quite a bit of similarity, but in the dynamical systems literature the precise connection does not seem to be heavily emphasised. The purpose of this post is to record the precise fashion in which dynamical systems cohomology is a special case of cochain complex cohomology from algebraic topology, and more specifically is analogous to singular cohomology (and can also be viewed as the group cohomology of the space of scalar-valued functions on X, when viewed as a G-module); this is not particularly difficult, but I found it an instructive exercise (especially given that my algebraic topology is extremely rusty), though perhaps this post is more for my own benefit that for anyone else.
— Chains —
Throughout this discussion, the dynamical system X, the group G, and the group U will be fixed.
For any , we define an n-chain to be a formal integer linear combination of n+1-tuples
, where
and
. One may wish to think of each such tuple as an “oriented simplex” connecting the n+1 points
. Thus, a 0-chain is a formal combination
of points, a 1-chain is a formal combination
of “line segments” from
to
, and so forth. Let
be the space of n-chains; this is an abelian group. We also adopt the convention that
is trivial for
, we define the boundary map
to be the unique homomorphism such that
thus for instance
and so forth. Note that this is analogous to the boundary map in singular homology, if one views the n+1-tuple as a simplex as discussed earlier. We also define the boundary maps
for
to be the trivial map, thus for instance
. It is not hard to verify the fundamental relation
thus turning the sequence of groups into a chain complex.
An n-chain with vanishing boundary is called an n-cycle, while an n-chain which is the boundary of an (n+1)-chain is called an n-boundary; the spaces of n-cycles and n-boundaries are denoted and
respectively. Thus for instance
is both a 1-cycle and a 1-boundary. However, if g is a non-trivial group element that fixes x and G is abelian, one can show that
is a 1-cycle but not a 1-boundary.
We define the homology groups for all n. It is a nice exercise to compute these groups in some simple cases, e.g.
- If G acts transitively on X, then
.
- If G acts freely on X, then
is trivial for
.
- If X is a point, then
is the abelianisation of G. [Question: Is there a nice description of the higher homology groups
,
in this case?]
However, I don’t know of any application of these homology groups to the theory of dynamical systems.
— Cochains —
An n-cochain is a homomorphism from the space of n-chains to U. Since
is a free abelian group generated by the simplices
, we can view an n-cochain as a function
from
to U. (Again, we are ignoring all measure-theoretic or topological considerations here.) The space of all n-cochains is denoted
; this is an abelian group.
The boundary map defines by duality a coboundary map
, defined by the formula
for all and
; viewing F as a function on simplices, we thus have
Thus for instance
for 0-cochains ,
for 1-cochains , and so forth.
Because , we have
, and so
becomes a cochain complex. n-cochains whose coboundary vanishes are known as n-cocycles, and n-cochains which are the coboundary of an (n-1)-cochain are known as n-coboundaries. The spaces of n-cocycles and n-coboundaries are denoted
and
respectively, allowing us to define the
cohomology group
.
When n=0, and if the action of G is transitive (in the discrete category), minimal (in the topological category), or ergodic (in the measure-theoretic category), the only 0-cocycles are the constants, and the only 0-coboundary is the zero function, so . When n=1, it is not hard to see that the notion of 1-cocycle and 1-coboundary correspond to the notion of cocycle and coboundary discussed at the beginning of this post.
This whole theory raises the obvious question as to whether the higher cocycles, coboundaries, and cohomology groups have any relevance in dynamical systems. For instance, a 2-cocycle is (after minor notational changes) a function that obeys the 2-cocycle equation
while a 2-coboundary is a function of the form
for some . Is there some dynamical systems interpretation of these objects, much as 1-cocycles and 1-coboundaries can be interpreted as describing abelian extensions and essentially trivial abelian extensions respectively? I don’t know the answer to this question. (Perhaps one would have to start introducing the concept of a “2-dynamical system”, whatever that means.) In my forthcoming paper with Vitaly Bergelson and Tamar Ziegler, we do briefly encounter 2-coboundaries (we have to deal with various “quasi-cocycles” – 1-chains
whose 2-coboundary
does not vanish completely, as with 1-cocycles, but is still of a relatively simple form, such as a constant or a polynomial) but we do not make systematic use of this concept. (We also rely heavily in our paper on the cubic complexes
of Host and Kra, which have some superficial resemblance to the simplex structures appearing here, but I do not know if there is a substantive connection in this regard.)
Another oddity is that homology and cohomology, as it is classically defined, requires the space of chains, cochains, etc. to all be abelian groups; but for dynamical systems one can certainly talk about cocycles and coboundaries taking values in a non-abelian group U by modifying the definitions slightly, leading to the concept of a group extension of a dynamical system. (In this context, the first cohomology becomes a quotient space rather than a group; see also my earlier post interpreting these cocycles in the language of gauge theory.) It seems to me that in this case, the dynamical system concept of a cocycle or coboundary cannot be interpreted in terms of classical cohomology theory (but presumably can be handled by non-abelian group cohomology).
[Update, Dec 22: Some typos and LaTeX anomalies fixed.]
Update, Jan 8: Over at the n-Category Café, Minhyong Kim has provided a nice answer to my question about the relevance of higher order cohomology, such as , to the problem of extending dynamical systems. Suppose one has a short exact sequence
of abelian groups, thus one can view as the space of pairs
with
with some group addition law
(2)
for some function , that needs to obey a certain set of axioms to make
an abelian group, which we will not write down here. We then claim that we have a long exact sequence
, (3)
thus is capable of detecting whether a U-extension of a G-system X can be lifted to a
-extension.
The first map in (3) is obvious: the projection from to
induces a projection from 1-cocycles
to 1-cocycles
which maps 1-coboundaries to 1-coboundaries, and thus maps
to
. The second map requires a bit more thought. Suppose one is given a 1-cocycle
and asks whether it can be lifted to a 1-cocycle
by the above projection. Writing
for some
and using (1), (2), we see that the question is equivalent to finding a
that obeys the equation
or in other words, to show that the map is a V-valued 2-coboundary. The same observation (now setting
) shows that the map
is a
-valued 2-coboundary (indeed, it is the coboundary of
), hence a
-valued 2-cocycle, and thus
is a V-valued 2-cocycle, and so the map
is a map from 1-cocycles
to 2-cocycles
. Similarly, given two 1-cocycles
, we see that
differs from
by some V-valued 1-cochain, so on taking derivatives we see that
differs from
by some 2-coboundary, thus
is linear modulo 2-coboundaries. Finally, if
is a U-valued 1-coboundary, then
is the sum of a
-valued 1-coboundary and a V-valued 1-cochain, and so on taking derivatives we see that
maps 1-coboundaries to 2-coboundaries. (Presumably the above arguments are a special case of one of the standard diagram chasing lemmas in homological algebra, but I don’t know which one it is. One could also verify these facts from the axioms of B induced from (2) and the abelian group structure on
, but this turns out to be remarkably tedious.) Hence it induces a map from
to
, and then (3) is exact by the preceding discussion.

26 comments
Comments feed for this article
21 December, 2008 at 10:57 pm
AA
Minor typo: Fourth paragraph, first sentence should probably read “While every coboundary is a cocycle, the converse is not always true.”
21 December, 2008 at 11:49 pm
hilbertthm90
Thanks! This is the first post in a long while that’s in a field I could follow. I actually just posted on a similar thing but was giving results about cohomology groups of Galois groups. Actually, the real reason I came down here was to post the typo someone else already caught, then decided to actually comment anyway.
22 December, 2008 at 5:01 am
Mikael Vejdemo Johansson
The boundary formula you have listed above comes from a slightly more general formula by using specific choices for group actions from the left and the right on the modules considered – thus, with a slightly more general formula, we’d have , and
, and 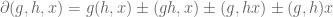 , et.c.
, et.c.
Would these formulae make sense in the dynamical systems world at all? Or is there nothing to be gained from extending to bimodules?
22 December, 2008 at 8:11 am
Marlowe, PI
Dear Terry:
I’m starting my thesis on certain cohomology theories, and it’s nice to find applications of the ideas in such diverse fields, specially since right now I’m focusing in the algebraic machinery and sometimes “real life” gets too blurred behind it.
As far as applications of higher cohomological groups goes, there seems to be a certain regularity in that if a certain cohomology group helps to classify extensions up to conjugation, the next cohomology group helps you find out if a certain candidate for an extension CAN be extended to a full extension. The most common example is when you want to deform a certain geometrical structure: you have a sequence of deformation parameters (each a cochain), and if you have a finite number of cochains you think might be the first part of a series, you can look at an associated cochain in the next cohomology group, pray for it to be zero, and if it is, that means the sequence can be continued one more step (in a possibly non unique way). The last paragraph might perhaps point in that direction?
8 July, 2016 at 4:51 pm
isomorphismes
Mark ____ (50centfunctions on tumblr) came up with a nice real-life dynamical system where the left and right inverses (thought of as undoing earlier-time moves or later-time moves) are noticeably different: touching up a billboard that’s been faded by the sun (right inverse), versus painting a billboard so that it will fade into the desired image (left inverse).
http://isomorphism.es/post/109259777716/good-example-of-a-function-from-real-life
22 December, 2008 at 8:18 am
Terence Tao
Thanks for the correction! I suppose the analogue of a bimodule in dynamical systems would be a space X with both a left and right action of a group G, which commute with each other; but I don’t know of any interesting example of this other than that when X is basically G itself (or maybe a quotient of G by a normal subgroup), in which case one is really doing group cohomology rather than dynamical systems.
19 October, 2023 at 10:06 am
Anonymous
There is a beautiful example of a bimodule in complex dynamics that first emerges in the `twisted rabbit’ problem. For concreteness consider a quadratic polynomial f(z) = z^2+c such that the forward orbit P(f) of 0 consists of exactly 3 points and f^3(0)=0. There are exactly 3 such polynomials; call this set S.
(The elements of S are often called the rabbit, the basilica, and the co-rabbit, based on the shape of their Julia sets.)
Now the space B of branched coverings of the plane admits an action of G, the mapping class group of the plane rel P(f), on the right and the left. Namely you can form the new map hfg(z) = h(f(g z)). The topological map hfg is combinatorial equivalent to a unique polynomial, which must be one of those in S. Predicting which element of S corresponds to, say h^n f, where h is a Dehn twist, is a delicate problem solved by Bartholdi and Nekrashevych in 2006. It involves a fairly complete description of the G-bimodule B. For a recent development and some illustrations, see:
Click to access TwistedRabbitTalkMichigan.pdf
-CTM
23 December, 2008 at 4:11 pm
Peter
It looks like you can also obtain this definition of homology using Hochshild homology (although someone should correct me if I’m not being careful enough). Given a ring and a bimodule
and a bimodule  , define
, define  , and for each
, and for each  the maps
the maps  for
for  by
by
with the nth boundary
To recover the homology defined in the post in the case of a group acting on a space
acting on a space  , I think you can take
, I think you can take  to be the group ring
to be the group ring  and
and  to be the free abelian group generated by points in
to be the free abelian group generated by points in  . The left module structure is given by the group action and the right module structure is the trivial structure.
. The left module structure is given by the group action and the right module structure is the trivial structure.
This is really just using slightly different language to describe the same thing, I suppose, but I guess in math writing problems or definitions in slightly different language is useful sometimes. Looking at it this way makes it seem a little bit more likely that it might be useful looking at right actions of other than the trivial one. I don’t know much about dynamical systems, so I’m not sure if it could actually be useful or not.
other than the trivial one. I don’t know much about dynamical systems, so I’m not sure if it could actually be useful or not.
25 December, 2008 at 7:56 am
Surya
I am thinking what all this means for information and coding theory. I had always wanted to build a geometric version of information theory based on a “cohomology” of dynamical systems. This cohomology might be a suitable candidate for that….
6 June, 2016 at 11:56 am
Pierre baudot
May be this paper could give an answer to the cohomological meaning for information:
http://www.mdpi.com/1099-4300/17/5/3253
6 June, 2016 at 12:01 pm
Pierre baudot
PS: The cohomology of information functions is constructed on Hochshild’s introduced by Peter in the last two posts and allows a unique characterisation of Shannon entropy.
8 January, 2009 at 2:22 am
David Corfield
This post was briefly discussed over at our blog.
8 January, 2009 at 4:04 pm
Terence Tao
Thanks David! I’ve taken the liberty of putting one of the comments on that blog posting (which answered one of my questions) in an update to the body of the post here. As Marlowe already predicted, the second cohomology group detects obstructions to a partial extension of a dynamical system lifting to a full extension.
19 January, 2009 at 11:34 am
An inverse theorem for the uniformity seminorms associated with the action of F^infty_p « What’s new
[…] as coboundaries, and two cocycles which differ by a coboundary are said to be cohomologous [see my previous post for further discussion]. Thus, our task is to show the cocycle is cohomologous to a phase […]
27 June, 2009 at 4:05 am
Adam Epstein
V. Nekresheych develops the notion of permutational bimodule, with many examples and applications, in his book “Self-Similar Groups”.
20 May, 2010 at 9:44 pm
254B, Notes 5: The inverse conjecture for the Gowers norm I. The finite field case « What’s new
[…] expression is known as a -coboundary (see this blog post for more discussion). To eliminate it, we use the finite characteristic to discretise the problem […]
17 July, 2010 at 12:20 pm
The cohomological equation for dynamical systems « Climbing Mount Bourbaki
[…] that I’m working on, so I shall not spend much time on it, though. Readers should look at this post on Terence Tao’s blog for more in this […]
7 June, 2011 at 7:32 am
Central extensions of Lie groups, and cocycle averaging « What’s new
[…] functions that obey this equation as cocycles (the reason for this terminology being explained in this previous blog post). The space of all such cocyles is denoted (or , if we wish to emphasise that we are working for […]
5 March, 2013 at 11:48 am
Freddie Manners
Rather a late correction, but in the section “cochains”, on the line just before the text “for 1-cochains $\rho : G \times H \rightarrow U”, I think there should be a $\rho(h, x)$ in place of a $\rho(g, x)$.
[Corrected, thanks – T.]
7 February, 2016 at 2:17 am
Trent Knebel
I don’t speak portuguese, but I wish I did because this mini-course on dynamical cohomology looks really interesting: https://www.youtube.com/playlist?list=PLo4jXE-LdDTT_z9urUQjYxl0uonw9xcBV
27 November, 2016 at 11:30 pm
mma
Dear Terry, I’m not a matematician, and just trying to make aquaintaince with homology and cohomology. Unfortunately, I don’t understand your singular cohomolgy analogy. For example, how do I derive your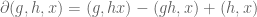 equation, based on this analogy? As far as I see,
equation, based on this analogy? As far as I see,  corresponds to the
corresponds to the  simplex, and the boundary of this (as the boundary of a simplicial complex) is
simplex, and the boundary of this (as the boundary of a simplicial complex) is  . How do your
. How do your  expression follow from this? Woould you explain this, please?
expression follow from this? Woould you explain this, please?
28 November, 2016 at 10:17 am
Terence Tao
To avoid confusion let’s use square brackets rather than parentheses to denote simplices. Then the identifications are
so in particular
and so the group boundary equation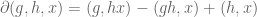 corresponds to the simplicial boundary equation
corresponds to the simplicial boundary equation ![[x,hx,ghx] = [hx,ghx] - [x,ghx] + [x,hx]](https://s0.wp.com/latex.php?latex=%5Bx%2Chx%2Cghx%5D+%3D+%5Bhx%2Cghx%5D+-+%5Bx%2Cghx%5D+%2B+%5Bx%2Chx%5D&bg=ffffff&fg=545454&s=0&c=20201002) .
.
28 November, 2016 at 12:57 pm
mma
Yes, as you guessed, I tried to convert the members in the wrong direction. Your squere brackets solved my confusion. Thank you very much, Terry!
5 December, 2016 at 11:26 pm
mma
I think that this correspondence is very similar to the “bar resolution” in Maclane’s Homology, (p.118, (5,11)), However, the numbering and the useage of square brackets and parentheses are opposite there.
8 July, 2018 at 8:08 am
1% quasimorphisms and group cohomology | What's new
[…] general, one can phrase this problem in the language of group cohomology (discussed in this previous post). Call a map a -cocycle. A -cocycle is a map obeying the […]
2 October, 2018 at 7:49 pm
Cohomologous functions and the Livsic theorem | Vaughn Climenhaga's Math Blog
[…] Remark 1 For a discussion of how this is connected to the notion of cohomology in algebraic topology, see Terry Tao’s blog post from December 2008. […]