Vitaly Bergelson, Tamar Ziegler, and I have just uploaded to the arXiv our paper “An inverse theorem for the uniformity seminorms associated with the action of “. This paper establishes the ergodic inverse theorems that are needed in our other recent paper to establish the inverse conjecture for the Gowers norms over finite fields in high characteristic (and to establish a partial result in low characteristic), as follows:
Theorem. Let
be a finite field of characteristic p. Suppose that
is a probability space with an ergodic measure-preserving action
of
. Let
be such that the Gowers-Host-Kra seminorm
(defined in a previous post) is non-zero.
- In the high-characteristic case
, there exists a phase polynomial g of degree <k (as defined in the previous post) such that
.
- In general characteristic, there exists a phase polynomial of degree <C(k) for some C(k) depending only on k such that
.
This theorem is closely analogous to a similar theorem of Host and Kra on ergodic actions of , in which the role of phase polynomials is played by functions that arise from nilsystem factors of X. Indeed, our arguments rely heavily on the machinery of Host and Kra.
The paper is rather technical (60+ pages!) and difficult to describe in detail here, but I will try to sketch out (in very broad brush strokes) what the key steps in the proof of part 2 of the theorem are. (Part 1 is similar but requires a more delicate analysis at various stages, keeping more careful track of the degrees of various polynomials.)
— A model case —
The theorem needs to be proven for all functions f with non-zero Gowers-Host-Kra norm in all ergodic systems, but to simplify the exposition let us look at a fairly specific type of function in a fairly specific type of system. Namely, we will assume that the system X is a circle extension of another ergodic
-system Y by a cocycle
, i.e. a measurable function obeying the cocycle identity
(1)
for all and almost every
. The circle extension X is defined as the Cartesian product
with shift map
(here we abuse notation a bit and use
to simultaneously denote the action on X and on Y). The function
we shall pick is the vertical coordinate function
.
Finally, we make the assumption that the base space Y (or more precisely, its -algebra) is already generated by phase polynomials of bounded degree.
Very roughly speaking, we can reduce the general case to the above case by an induction on k, together with some standard theory of Mackey and Furstenberg on isometric extensions and group extensions (cf. my lectures on the topological dynamics counterpart to these topics), and of Furstenberg-Weiss on characteristic factors, together with some Fourier analysis to reduce matters from (abelian) group extensions to circle extensions. These reductions are standard in the ergodic theory literature, but somewhat technical, and I will not discuss them further here.
— Cocycles and coboundaries —
Our task is to show that the vertical coordinate function , which we assume to have non-zero Gowers-Host-Kra seminorm, correlates with some bounded degree polynomial. To do this, it suffices to express the cocycle
in the form
(2)
for some measurable functions ,
, where
and
is a phase polynomial of bounded degree for each
. Indeed, we can rearrange (2) as
and so all derivatives of are phase polynomials of bounded degree, which implies that
is itself a phase polynomial of bounded degree, thus
is the product of F with a phase polynomial of bounded degree. But
, which is generated by phase polynomials of bounded degree, and so
can be approximated by a linear combination of phase polynomials of bounded degree, and thus in particular must correlate with at least one of them, as desired.
It thus remains to establish (2). Cocycles of the form are known as coboundaries, and two cocycles which differ by a coboundary are said to be cohomologous [see my previous post for further discussion]. Thus, our task is to show the cocycle
is cohomologous to a phase polynomial of bounded degree.
— The finite type condition —
We have yet to use the hypothesis that the vertical coordinate function has non-zero
norm. For this, we use a key observation of Host-Kra that this hypothesis implies (in fact it is basically equivalent to) a certain finite type condition on the cocycle
. We derive this condition somewhat informally as follows. If
is non-zero, then this means that the expected value of the expression
(3)
is non-zero, where ranges over “k-dimensional parallelopipeds” in X. (This can be made precise by using the cubic measures
of Host and Kra, but let us ignore this technical detail here.)
One way to make a k-dimensional parallelopiped is to start with a (k-1)-dimensional parallelopiped , shift it by a group element g, and glue the two (k-1)-dimensional parallelopipeds together. When one does so, the quantity (3) simplifies to
. (4)
Note that as does not depend on the vertical coordinate u, one can view the
as living in Y rather than in X.
We expect (4) to have a non-zero average in some sense. If we define the limiting average
(where denotes the limit after averaging g along a Følner sequence) we thus expect F to be non-zero at least some of the time; to simplify the discussion let us pretend that it is in fact always non-zero. The cocycle equation (1) implies that
and so, after defining , we see that
is a coboundary:
. (5)
When obeys this condition, we say that it is of type
. The challenge is now to “integrate” the derivative
out of (5) and obtain (2).
— Vertical differentiation —
The parallelopiped-based derivatives are difficult to work with directly (unless k is very small). It is convenient to replace them with a simpler type of derivative, a “vertical” derivative. To explain this, we first decompose Y as an extension
of a “simpler” system Z (where “simpler” means, roughly speaking, that we can generate it using polynomials of strictly lower degree than what one needs for Y), where U is a compact abelian group and
is a cocycle. It turns out that we can always decompose Y in this fashion, because Y is generated by polynomials; furthermore we can make the cocycle
a polynomial of bounded degree.
Once one does this, the system Y not only has an action of , but also has an action of the vertical group U, which commutes with the
action. Given any
, we can now define the vertical derivative
of any function
by the formula
It turns out that the general theory of cubic measures, as worked out by Host and Kra, allows one to relate vertical derivatives to the parallelogram derivatives
(basically, the point is that the group U happens to preserve the cubic measures
when applied correctly). Because of this, it is possible to deduce from (5) the “Conze-Lesigne type” equation
(5′)
for all . This equation is more tractable than (5) for a number of reasons, one of which being that y now lives in the system Y, rather than being a
-dimensional parallelopiped of points in Y. Our task is now to repeatedly integrate away the vertical derivatives on the left-hand side of (5′) to obtain (2).
This procedure will be done one derivative at a time. Let us focus on the final step. For this, we assume that we have already obtained an equation of the form
(5”)
for all , and almost every
, where
is a phase polynomial of bounded degree and
is a measurable function taking values in
; thus every vertical derivative of
is cohomologous to a bounded degree phase polynomial. (A technical but important point: it is possible to select
and
so that
is jointly measurable in both u and y, and similarly for
. This is ultimately possible because the space of bounded degree phase polynomials turns out to be discrete modulo constants.) The task is now to integrate (5”) to obtain (2). Actually, we will establish a weaker form of (2), namely
(6)
where and
is some measurable function. One can show that if (6) holds, then
obeys similar properties to the cocycle
, in particular the finite type condition (5). (It turns out to not quite be a cocycle, though, but merely a quasi-cocycle: a cocycle modulo phase polynomials. This is an important technical difficulty, but let us ignore it for this discussion.) Since Z is a simpler system than Y, it is possible to combine (6) with a suitable inductive argument to recover (2).
To summarise our progress so far, we are now at the point where every vertical derivative of is cohomologous to a polynomial (equation (5”)), and wish to integrate this information to conclude that
itself is cohomologous to a polynomial, times a vertically-invariant function.
— Reduction to the finite U case —
We now analyse the equation (5”) further. We have a cocycle relation
where denotes the action of vertical rotation by u. Inserting this relation into our hypothesis (5”), we see that
is a phase polynomial of bounded degree, and thus
is also a phase polynomial of bounded degree. In other words,
is a quasi-cocycle in u; it obeys the cocycle equation
modulo phase polynomials of bounded degree.
Suppose temporarily that was a genuine cocycle in u. Then, it is possible (using some Fourier analysis) to conclude that
is in fact a coboundary in u,
; this is basically because the action of U on Y is free and thus has no non-trivial cohomology. (One can get some idea of this by looking at the case when U and Y are finite.) We can now rewrite (5”) as
.
In particular, must be a cocycle in U, and is thus also a coboundary:
. Since the
are phase polynomials of bounded degree, and the cocycle
underlying the extension
is also a phase polynomial of bounded degree, it is possible to ensure that the “antiderivative” P of the
of the phase polynomials of bounded degree is also a polynomial of bounded degree. (Verifying this “integration lemma” requires a certain amount of algebraic computation – analogous to that required to show that the composition of two polynomials is again a polynomial, as was done for instance in this previous post of mine – but we will ignore this issue here.) We thus see that
has vanishing u derivative for every U, and is thus of the form
for some
, thus yielding (5”) as desired. Thus we see that we would be done if F was a genuine cocycle in U.
Unfortunately, F is only a quasi-cocycle in U; the cocycle equation only holds modulo phase polynomials. However, one can show that the space of phase polynomials (after quotienting out by constants) is discrete and thus at most countable. (This discreteness is closely related to the local testability of polynomials that was mentioned in a previous post.) Because of this, and the countable pigeonhole principle, we can find a single polynomial P for which the modified cocycle equation holds (modulo constants) for a set E of (u,v) of positive measure in
.
Now let us recall a basic fact from measure theory: if E is a positive measure subset of a compact abelian group U, then the difference set E-E contains an open neighbourhood of the origin. (This is basically because sets of positive measure can be approximated by open sets, as per Littlewood’s principle.). Using facts like this, and manipulating the above modified cocycle equation a few times, one eventually arrives at the conclusion that F is in fact a genuine cocycle on an open neighbourhood of the origin in U. (Here I am oversimplifying a number of technical details, which can be found in the paper. I will mention though that it was crucial here that was measurable in u, a fact alluded to earlier.)
Up until now, we have not used at all any properties of the underlying group (other than that it is abelian, discrete, and amenable). Now, for the first time, we exploit the finite characteristic. Because of this finite characteristic, all phase polynomials take values in roots of unity (modulo constants); since Y is given by polynomials, it is possible to show that U is then a torsion group (in fact, one can show it is the direct product of at most countably many cyclic groups). As a consequence of this, every open neighbourhood of the origin in U contains an open subgroup. Thus, we have managed to show that
is a cocycle, not for
, but rather for
where U’ is an open subgroup of U.
This is close enough to what we originally wanted that we can try repeating the above arguments. Doing this, we find at the end of the day that we can “quotient out” U’ from the problem and effectively reduce U to the quotient group U/U’. Since U is compact and U’ is open, U/U’ is finite. Thus, we have effectively reduced matters to the case in which U is finite.
— The finite U case —
Now let U be finite. The classification of finite abelian groups tells us that U is the product of cyclic groups. For simplicity let us suppose that U is a single cyclic group, and specifically the group of
roots of unity; this is not the most general case, but it illustrates the method (the general case is handled by a more complicated version of the arguments below).
Let e be the generator of U, thus . By the previous arguments, we know that F is a quasi-cocycle in U, thus
(6)
for some phase polynomial of bounded degree. We would like to eliminate the polynomials
from this equation to get a genuine cocycle.
We can partially do this by redefining the for
in terms of
by the formula
. (7)
One can show (using (6)) that this redefinition does not significantly affect (5”), and now we have the exact cocycle condition
(8)
whenever and
. However, (8) need not hold for all j, k. In order for this to be true, one must obey the line cocycle condition
(9)
(which would make the definition in (7) periodic in j). Conversely, if (9) holds then the cocycle given by (7) is a true cocycle in U, thus this condition completely describes the “cohomology” of U-cocycles here.
Now, in general, the that we initially start with need not satisfy (9). However, by using (6), one can show that the left-hand side of (9), while not identically 1, is at least a phase polynomial of bounded degree. At this point we use a key algebraic lemma (which I hope to comment more on in a future post): every phase polynomial of bounded degree has a
root which is also a phase polynomial of bounded (but slightly higher) degree. Thus we have
for some polynomial Q of bounded degree. But then what we can do is divide each by Q; this does not significantly affect (5”), but now recovers the line cocycle condition (9), and allows us to make
a cocycle on U, at which point one can argue as before.
The multidimensional case, when U is a product of cyclic groups, is a little more sophisticated than this; in addition to the line cocycle condition (9), there is an additional “zero curvature” condition that has to be obtained before one can build a cocycle in U, but it turns out that a suitably multidimensional generalisation of the formula (7) can ensure this.

9 comments
Comments feed for this article
20 January, 2009 at 1:18 am
bengreen
A tour de force which I shall enjoy reading on a forthcoming train journey. But please, please can you think of an alternative to the triangle-with-a-dot notation for multiplicative derivative?
20 January, 2009 at 5:02 am
Tom
Dear Terry, the paper is extremely well written and indeed a joy to read (even to an outsider like me). One typo: on page 8 (eq 1.2) there’s an extra 0 in the matrix.
Do you expect the sharpest constant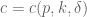 in theorem 1.27 to have a nice explicit form (at least for k=1 or k=p)?
in theorem 1.27 to have a nice explicit form (at least for k=1 or k=p)?
Finally I’d humbly concur that the current notation for the multiplicative derivative is a bit heavy to the eye, a trick to make the black dot a little smaller would to use the \scriptscriptsize command, here’s a wordpress try without preview: either this or that
or that  .
.
20 January, 2009 at 9:32 am
Terence Tao
Thanks for the correction! We actually had a lot of trouble deciding on the notation for the multiplicative derivative; we had considered or
or  or
or  but felt that the dots were too inconspicuous. I guess we erred in the other direction instead. I like the scriptsize idea (though my version of LaTeX is so far refusing to acknowledge \scriptscriptsize), I’ll try to see if I can centre the dot in the middle of the triangle. [update: OK, I managed to jerry rig this:
but felt that the dots were too inconspicuous. I guess we erred in the other direction instead. I like the scriptsize idea (though my version of LaTeX is so far refusing to acknowledge \scriptscriptsize), I’ll try to see if I can centre the dot in the middle of the triangle. [update: OK, I managed to jerry rig this:  .]
.]
(Alternatively, since we use multiplicative differentiation far more often than additive differentiation, another option is to make default to multiplicative and use some other notation for additive. But we felt that this might be confusing since
default to multiplicative and use some other notation for additive. But we felt that this might be confusing since  denotes additive differentiation in many other places in the literature. Anyway, I welcome further suggestions.)
denotes additive differentiation in many other places in the literature. Anyway, I welcome further suggestions.)
14 December, 2009 at 3:38 pm
Approximate bases, sunflowers, and nonstandard analysis « What’s new
[…] with respect to the shift . (This need to consider families is an issue that also comes up in the finite field ergodic theory analogue of the inverse conjectures, due to the unbounded number of generators in that case, but […]
20 May, 2010 at 9:45 pm
254B, Notes 5: The inverse conjecture for the Gowers norm I. The finite field case « What’s new
[…] handle the general case, which was worked out in two papers, one by myself and Ziegler, and one by Bergelson, Ziegler, and myself. It turns out that it is convenient to phrase these arguments in the language of ergodic theory. […]
11 January, 2011 at 6:59 am
The inverse conjecture for the Gowers norm over finite fields in low characteristic « What’s new
[…] for the Gowers norm, this time for vector spaces over a fixed finite field of prime order; with Vitaly Bergelson, we had previously established this claim when the characteristic of the field was large, so the […]
21 May, 2013 at 4:30 pm
Multiple recurrence and convergence results associated to $F_{p}^{omega}$-actions | What's new
[…] analogue of the structural theory of Host and Kra was worked out by Vitaly, Tamar, and myself in these previous papers (treating the high characteristic and low characteristic cases respectively). In […]
27 May, 2022 at 2:14 pm
Notes on inverse theorem entropy | What's new
[…] prime order (so that ), then the inverse theorem of Ziegler and myself (available in both high and low characteristic) allows one to obtain an -inverse theorem for some and the collection of […]
10 March, 2023 at 8:59 am
A Host–Kra ${bf F}^omega_2$-system of order 5 that is not Abramov of order 5, and non-measurability of the inverse theorem for the $U^6({bf F}^n_2)$ norm; The structure of totally disconnected Host–Kra–Ziegler factors, and the inverse th
[…] of Towsner for a closely related principle, and this paper of Jamneshan and I for a refinement). In a paper with Bergelson and Ziegler, we were able to establish Conjecture 2 in the “high characteristic” case , thus also […]