For these notes, is a fixed measurable space. We shall often omit the
-algebra
, and simply refer to elements of
as measurable sets. Unless otherwise indicated, all subsets of X appearing below are restricted to be measurable, and all functions on X appearing below are also restricted to be measurable.
We let denote the space of measures on X, i.e. functions
which are countably additive and send
to 0. For reasons that will be clearer later, we shall refer to such measures as unsigned measures. In this section we investigate the structure of this space, together with the closely related spaces of signed measures and finite measures.
Suppose that we have already constructed one unsigned measure on X (e.g. think of X as the real line with the Borel
-algebra, and let m be Lebesgue measure). Then we can obtain many further unsigned measures on X by multiplying m by a function
, to obtain a new unsigned measure
, defined by the formula
. (1)
If is an indicator function, we write
for
, and refer to this measure as the restriction of m to A.
Exercise 1. Show (using the monotone convergence theorem) that is indeed a unsigned measure, and for any
, we have
. We will express this relationship symbolically as
.
(2)
Exercise 2. Let m be -finite. Given two functions
, show that
if and only if
for m-almost every x. (Hint: as usual, first do the case when m is finite. The key point is that if f and g are not equal m-almost everywhere, then either f>g on a set of positive measure, or f<g on a set of positive measure.) Give an example to show that this uniqueness statement can fail if m is not
-finite. (Hint: take a very simple example, e.g. let X consist of just one point.)
In view of Exercises 1 and 2, let us temporarily call a measure differentiable with respect to m if
(i.e.
) for some
, and call f the Radon-Nikodym derivative of
with respect to m, writing
; (3)
by Exercise 2, we see if is
-finite that this derivative is defined up to m-almost everywhere equivalence.
Exercise 3. (Relationship between Radon-Nikodym derivative and classical derivative) Let m be Lebesgue measure on , and let
be an unsigned measure that is differentiable with respect to m. If
has a continuous Radon-Nikodym derivative
, show that the function
is differentiable, and
for all x.
Exercise 4. Let X be at most countable. Show that every measure on X is differentiable with respect to counting measure .
If every measure was differentiable with respect to m (as is the case in Exercise 4), then we would have completely described the space of measures of X in terms of the non-negative functions of X (modulo m-almost everywhere equivalence). Unfortunately, not every measure is differentiable with respect to every other: for instance, if x is a point in X, then the only measures that are differentiable with respect to the Dirac measure are the scalar multiples of that measure. We will explore the precise obstruction that prevents all measures from being differentiable, culminating in the Radon-Nikodym-Lebesgue theorem that gives a satisfactory understanding of the situation in the
-finite case (which is the case of interest for most applications).
In order to establish this theorem, it will be important to first study some other basic operations on measures, notably the ability to subtract one measure from another. This will necessitate the study of signed measures, to which we now turn.
[The material here is largely based on Folland’s text, except for the last section.]
— Signed measures —
We have seen that if we fix a reference measure m, then non-negative functions (modulo m-almost everywhere equivalence) can be identified with unsigned measures
. This motivates various operations on measures that are analogous to operations on functions (indeed, one could view measures as a kind of “generalised function” with respect to a fixed reference measure m). For instance, we can define the sum of two unsigned measures
as
(4)
and non-negative scalar multiples for
by
. (5)
We can also say that one measure is less than another
if
for all
. (6)
These operations are all consistent with their functional counterparts, e.g. , etc.
Next, we would like to define the difference of two unsigned measures. The obvious thing to do is to define
(7)
but we have a problem if and
are both infinite:
is undefined! To fix this problem, we will only define the difference of two unsigned measures
if at least one of them is a finite measure. Observe that in that case,
takes values in
or
, but not both.
Of course, we no longer expect to be monotone. However, it is still finitely additive, and even countably additive in the sense that the sum
converges to
whenever
are disjoint sets, and furthermore that the sum is absolutely convergent when
is finite. This motivates
Definition 1. (Signed measure) A signed measure is a map
such that
;
can take either the value
or
, but not both;
- If
are disjoint, then
converges to
, with the former sum being absolutely convergent if the latter expression is finite. [Actually, the absolute convergence is automatic from the Riemann rearrangement theorem. Another consequence of 3. is that any subset of a finite measure set is again finite measure, and the finite union of finite measure sets again has finite measure.]
Thus every unsigned measure is a signed measure, and the difference of two unsigned measures is a signed measure if at least one of the unsigned measures is finite; we will see shortly that the converse statement is also true, i.e. every signed measure is the difference of two unsigned measures (with one of the unsigned measures being finite). Another example of a signed measure are the measures defined by (1), where
is now signed rather than unsigned, but with the assumption that at least one of the signed parts
,
of f is absolutely integrable.
We also observe that a signed measure is unsigned if and only if
(where we use (6) to define order on measures).
Given a function , we can partition X into one set
on which f is non-negative, and another set
on which f is negative; thus
and
. It turns out that the same is true for signed measures:
Theorem 1. (Hahn decomposition theorem) Let
be a signed measure. Then one can find a partition
such that
and
.
Proof. By replacing with
if necessary, we may assume that
avoids the value
.
Call a set E totally positive if , and totally negative if
. The idea is to pick
to be the totally positive set of maximal measure – a kind of “greedy algorithm”, if you will. More precisely, define
to be the supremum of
, where E ranges over all totally positive sets. (The supremum is non-vacuous, since the empty set is totally positive.) We claim that the supremum is actually attained. Indeed, we can always find a maximising sequence
of totally positive sets with
. It is not hard to see that the union
is also totally positive, and
as required. Since
avoids
, we see in particular that
is finite.
Set . We claim that
is totally negative. We do this as follows. Suppose for contradiction that
is not totally negative, then there exists a set
in
of strictly positive measure. If
is totally positive, then
is a totally positive set having measure strictly greater than
, a contradiction. Thus
must contain a subset
of strictly larger measure. Let us pick
so that
, where
is the smallest integer for which such an
exists. If
is totally positive, then we are again done, so we can find a subset
with
, where
is the smallest integer for whch such a
exists. Continuing in this fashion, we either stop and get a contradiction, or obtain a nested sequence of sets
in
of increasing positive measure (with
). The intersection
then also has positive measure, hence finite, which implies that the
go to infinity; it is then not difficult to see that E itself cannot contain any subsets of strictly larger measure, and so E is a totally positive set of positive measure in
, and we again obtain a contradiction.
Remark 0. A somewhat simpler proof of the Hahn decomposition theorem is available if we assume to be finite positive variation (which means that
is bounded above as E varies). For each positive n, let
be a set whose measure
is within
of
. One can easily show that any subset of
has measure
, and in particular that
has measure
for any
. This allows one to control the unions
, and thence the lim sup
of the
, which one can then show to have the required properties. One can in fact show that any signed measure that avoids
must have finite positive variation, but this turns out to require a certain amount of work.
Let us say that a set E is null for a signed measure if
. (This implies that
, but the converse is not true, since a set E of signed measure zero could contain subsets of non-zero measure.) It is easy to see that the sets
given by the Hahn decomposition theorem are unique modulo null sets.
Let us say that a signed measure is supported on E if the complement of E is null (or equivalently, if
. If two signed measures
can be supported on disjoint sets, we say that they are mutually singular (or that
is singular with respect to
) and write
. If we write
and
, we thus soon establish
Exercise 5. (Jordan decomposition theorem) Every signed measure an be uniquely decomposed as
, where
are mutually singular unsigned measures. (The only claim not already established is the uniqueness.) We refer to
as the positive and negative parts (or positive and negative variations) of
.
This is of course analogous to the decomposition of a function into positive and negative parts. Inspired by this, we define the absolute value (or total variation)
of a signed measure to be
.
Exercise 6. Show that is the minimal unsigned measure such that
. Furthermore,
is equal to the maximum value of
, where
ranges over the partitions of E. (This may help explain the terminology “total variation”.)
Exercise 7. Show that is finite for every E if and only if
is a finite unsigned measure, if and only if
are finite unsigned measures. If any of these properties hold, we call
a finite measure. (In a similar spirit, we call a signed measure
-finite if
is
-finite.)
The space of finite measures on X is clearly a real vector space, and is denoted . (One can also complexify this space to obtain a complex vector space of complex finite measures, but we will not use such measures here.)
— The Lebesgue-Radon-Nikodym theorem —
Let m be a reference unsigned measure. We saw in the introduction that the map is an embedding of the space
of non-negative functions (modulo m-almost everywhere equivalence) into the space
of unsigned measures. The same map is also an embedding of the space
of absolutely integrable functions (again modulo m-almost everywhere equivalence) into the space
of finite measures. (To verify this, one first makes the easy observation that the Jordan decomposition of a measure
given by an absolutely integrable function f is simply
.)
In the converse direction, one can ask if every finite measure in
can be expressed as
for some absolutely integrable f. Unfortunately, there are some obstructions to this. Firstly, from (1) we see that if
, then any set that has measure zero with respect to
, must also have measure zero with respect to
. In particular, this implies that a non-trivial measure that is singular with respect to m cannot be expressed in the form
.
In the -finite case, this turns out to be the only obstruction:
Theorem 2. (Lebesgue–Radon-Nikodym theorem) Let m be an unsigned
-finite measure, and let
be a signed
-finite measure. Then there exists a unique decomposition
, where
is measurable and
. If
is unsigned, then f and
are also. If
is finite,
lies in
and
is finite.
Proof. We prove this only for the case when are finite rather than
-finite, and leave the general case as an exercise. The uniqueness follows from Exercise 2 and the previous observation that
cannot be mutually singular with m for any non-zero f, so it suffices to prove existence. By the Jordan decomposition theorem, we may assume that
is unsigned as well. (In this case, we expect f and
to be unsigned also.)
The idea is to select f “greedily“. More precisely, let M be the supremum of the quantity , where f ranges over all non-negative functions such that
. Since
is finite, M is finite. We claim that the supremum is actually attained for some f. Indeed, if we let
be a maximising sequence, thus
and
, one easily checks that the function
attains the supremum.
The measure is a non-negative finite measure by construction. To finish the theorem, it suffices to show that
.
It will suffice to show that for all
, as the claim then easily follows by letting
be a countable sequence going to zero. But if
were not singular with respect to m, we see from the Hahn decomposition theorem that there is a set E with
such that
, and thus
. But then one could add
to f, contradicting the construction of f.
Exercise 8. Complete the proof of Theorem 2 for the -finite case.
We have the following corollary:
Corollary 1. (Radon-Nikodym theorem) Let m be an unsigned
-finite measure, and let
be a signed finite measure. Then the following are equivalent.
for some measurable
.
whenever
.
- For every
, there exists
such that
whenever
.
When
is
-finite instead of finite, 1 and 2 are still equivalent.
When statement 1 or 2 (or 3, in the finite case) occurs, we say that
is absolutely continuous with respect to m, and write
. As in the introduction, we call f the Radon-Nikodym derivative of
with respect to m, and write
.
Proof. It suffices to establish the case when is finite. The implication of 3. from 1. is Exercise 11 from Notes 0. The implication of 2. from 3. is trivial. To deduce 1. from 2., apply Theorem 2 to
and observe that
is supported on a set of m-measure zero E by hypothesis. Since E is null for m, it is null for
and
also, and so
is trivial, giving 1.
Corollary 2. (Lebesgue decomposition theorem) Let m be an unsigned
-finite measure, and let
be a signed
-finite measure. Then there is a unique decomposition
, where
and
. (We refer to
and
as the absolutely continuous and singular components of
with respect to m.) If
is unsigned, then
and
are also.
Exercise 9. If every point in X is measurable, we call a signed measure continuous if
for all x. Let the hypotheses be as in Corollary 2, but suppose also that every point is measurable and m is continuous. Show that there is a unique decomposition
, where
,
is supported on an at most countable set, and
is both singular with respect to m and continuous. Furthermore, if
is unsigned, then
are also. We call
and
the singular continuous and pure point components of
respectively.
Example 1. A Cantor measure is singular continuous with respect to Lebesgue measure, while Dirac measures are pure point. Lebesgue measure on a line is singular continuous with respect to Lebesgue measure on a plane containing that line.
Remark 1. Suppose one is decomposing a measure on a Euclidean space
with respect to Lebesgue measure m on that space. Very roughly speaking, a measure is pure point if it is supported on a 0-dimensional subset of
, it is absolutely continuous if its support is spread out on a full dimensional subset, and is singular continuous if it is supported on some set of dimension intermediate between 0 and d. For instance, if
is the sum of a Dirac mass at
, one-dimensional Lebesgue measure on the x-axis, and two-dimensional Lebesgue measure on
, then these are the pure point, singular continuous, and absolutely continuous components of
respectively. This heuristic is not completely accurate (in part because I have left the definition of “dimension” vague) but is not a bad rule of thumb for a first approximation.
To motivate the terminology “continuous” and “absolutely continuous”, we recall two definitions on an interval , and make a third:
- A function
is continuous if for every
and every
, there exists
such that
whenever
is such that
.
- A function
is uniformly continuous if for every
, there exists
such that
whenever
has length at most
.
- A function
is absolutely continuous if for every
, there exists
such that
whenever
are disjoint intervals in I of total length at most
.
Clearly, absolute continuity implies uniform continuity, which in turn implies continuity. The significance of absolute continuity is that it is the largest class of functions for which the fundamental theorem of calculus holds (using the classical derivative, and the Lebesgue integral), as was shown in the previous course.
Exercise 10. Let m be Lebesgue measure on the interval , and let
be a finite unsigned measure.
- Show that
is a continuous measure if and only if the function
is continuous.
- Show that
is an absolutely continuous measure with respect to m if and only if the function
is absolutely continuous.
— A finitary analogue of the Lebesgue decomposition (optional) —
At first glance, the above theory is only non-trivial when the underlying set X is infinite. For instance, if X is finite, and m is the uniform distribution on X, then every other measure on X will be absolutely continuous with respect to m, making the Lebesgue decomposition trivial. Nevertheless, there is a non-trivial version of the above theory that can be applied to finite sets (cf. my blog post on the relationship between soft analysis and hard analysis). The cleanest formulation is to apply it to a sequence of (increasingly large) sets, rather than to a single set:
Theorem 3. (Finitary analogue of the Lebesgue-Radon-Nikodym theorem) Let
be a sequence of finite sets (and with the discrete
-algebra), and for each n, let
be the uniform distribution on
, and let
be another probability measure on
. Then, after passing to a subsequence, one has a decomposition
(9)
where
- (Uniform absolute continuity) For every
, there exists
(independent of n) such that
whenever
, for all n and all
.
- (Asymptotic singular continuity)
is supported on a set of
-measure
, and we have
uniformly for all
, where
denotes an error that goes to zero as
.
- (Uniform pure point) For every
there exists
(independent of n) such that for each n, there exists a set
of cardinality at most N such that
.
Proof. Using the Radon-Nikodym theorem (or just working by hand, since everything is finite), we can write for some
with average value 1.
For each positive integer k, the sequence is bounded between 0 and 1, so by the Bolzano-Weierstrass theorem, it has a convergent subsequence. Applying the usual diagonalisation argument (as in the proof of the Arzelà-Ascoli theorem), we may thus assume (after passing to a subsequence, and relabeling) that
converges for positive k to some limit
.
Clearly, the are decreasing and range between 0 and 1, and so converge as
to some limit
.
Since , we can find a sequence
going to infinity such that
as
. We now set
to be the restriction of
to the set
. We claim the absolute continuithy property 1. Indeed, for any
, we can find a k such that
. For n sufficiently large, we thus have
(10)
and
(11)
and hence
. (12)
If we take , we thus see (for n sufficiently large) that 1. holds. (For the remaining n, one simply shrinks delta as much as is necessary.)
Write , thus
is supported on a set of size
by Markov’s inequality. It remains to extract out the pure point components. This we do by a similar procedure as above. Indeed, by arguing as before we may assume (after passing to a subsequence as necessary) that the quantities
converge to a limit
for each positive integer j, that the
themselves converge to a limit d, and that there exists a sequence
such that
converges to d. If one sets
and
to be the restrictions of
to the sets
and
respectively, one can verify the remaining claims by arguments similar to those already given.
Exercise 11. Generalise Theorem 3 to the setting where the can be infinite and non-discrete (but we still require every point to be measurable), the
are arbitrary probability measures, and the
are arbitrary finite measures of uniformly bounded total variation.
Remark 2. This result is still not fully “finitary” because it deals with a sequence of finite structures, rather than with a single finite structure. It appears in fact to be quite difficult (and perhaps even impossible) to make a fully finitary version of the Lebesgue decomposition (in the same way that the finite convergence principle in this blog post of mine was a fully finitary analogue of the infinite convergence principle), though one can certainly form some weaker finitary statements that capture a portion of the strength of this theorem. For instance, one very cheap thing to do, given two probability measures , is to introduce a threshold parameter k, and partition
, where
, and
is supported on a set of m-measure at most
; such a decomposition is automatic from Theorem 2 and Markov’s inequality, and has meaningful content even when the underlying space X is finite, but this type of decomposition is not as powerful as the full Lebesgue decompositions (mainly because the size of the support for
is relatively large compared to the threshold k). Using the finite convergence principle, one can do a bit better, writing
for any function F and any
, where
,
,
is supported on a set of m-measure at most
, and
has total mass at most
, but this is still fails to capture the full strength of the infinitary decomposition, because
needs to be fixed in advance. I have not been able to find a fully finitary statement that is equivalent to, say, Theorem 3; I suspect that if it does exist, it will have quite a messy formulation.
[Update, Jan 5: Exercise added.]
[Update, Jan 7: Proof of Hahn decomposition theorem altered; my original proof works, but one of the steps was much trickier than I had anticipated, so I am reverting to Folland’s proof.]

74 comments
Comments feed for this article
16 March, 2022 at 7:20 am
J
Unfortunately, not every measure is differentiable with respect to every other: for instance, if x is a point in X, then the only measures that are differentiable with respect to the Dirac measure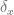 are the scalar multiples of that measure.
are the scalar multiples of that measure.
This remark in the notes may be changed to an exercise right after Exercise 4, which makes the Dirac measure a sharp contrast to the counting measure.
16 March, 2022 at 7:51 am
J
In the proof of Theorem 1:
 of totally positive sets with
of totally positive sets with  . It is not hard to see that the union
. It is not hard to see that the union 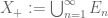 is also totally positive, and
is also totally positive, and 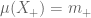 as required. Since
as required. Since  avoids
avoids 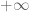 , we see in particular that
, we see in particular that 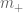 is finite.
is finite.
Indeed, we can always find a maximising sequence
In the last sentence, how does avoid
avoid 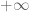 ?
?
16 March, 2022 at 9:59 am
Terence Tao
This reduction was obtained in the first sentence of the proof.
17 March, 2022 at 5:46 am
J
1. for
for 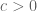 ” or “non-negative scalar multiples … for
” or “non-negative scalar multiples … for 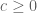 “.
“.
In (5), to be consistent, one either has “positive scalar multiples
2. It may be worth making a remark/exercise to mention complex measures. In 245A, one mostly deals with complex-valued functions . Also,
. Also, 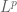 spaces are defined in notes 3, where one again uses complex-valued functions. The space
spaces are defined in notes 3, where one again uses complex-valued functions. The space  in the first paragraph under the title “The Lebesgue-Radon-Nikodym theorem”, however, consists of only real-valued functions. The measurable function
in the first paragraph under the title “The Lebesgue-Radon-Nikodym theorem”, however, consists of only real-valued functions. The measurable function  in Theorem 2 and Corollary 1 is also real-valued.
in Theorem 2 and Corollary 1 is also real-valued.
3.
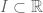 , and make a third: …
, and make a third: …
To motivate the terminology “continuous” and “singular continuous”, we recall two definitions on an interval
The following discussion seems to be more about “absolutely continuous” instead of “singular continuous”. Typo?
[Corrected, thanks – T.]
18 March, 2022 at 1:19 pm
Anonymous
Typo in the proof of Theorem 2:
We prove this only for the case when
[Corrected, thanks – T.]
14 June, 2022 at 10:59 am
Dingjun Bian
In the proof of Corollary 1 when deducing 1 from 2, did you meant quoting Theorem 2 instead of Theorem 1? Thank you.
[Corrected, thanks – T.]
17 June, 2022 at 4:05 am
N is a number
Prof. Tao when you refer to Folland’s text do you mean his book titled “Real analysis: Modern Techniques and Their Applications” ?
[Yes – T.]
17 June, 2022 at 7:57 am
Anonymous
yes.
17 June, 2022 at 4:45 am
N is a number
Prof. Tao in Exercise 2 is this the right way: almost everywhere, then either
almost everywhere, then either  or
or 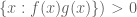 then there is some
then there is some 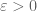 such that with
such that with 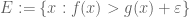 one has
one has 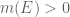 (otherwise take a sequence of positive reals
(otherwise take a sequence of positive reals  which converges to 0 and use countable additivity to get a contradiction). Now take a covering of
which converges to 0 and use countable additivity to get a contradiction). Now take a covering of  with measurable subsets of
with measurable subsets of  where each covering part has a finite
where each covering part has a finite  measure, then intersecting this covering parts with
measure, then intersecting this covering parts with  it follows that
it follows that 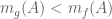 for some measurable
for some measurable 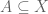 with
with 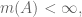 but this gives a contradiction.
but this gives a contradiction.
as you mention if f and g do not agree
Note: we required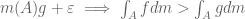 which is of course not true in general if
which is of course not true in general if  is infinite.
is infinite.
This gives us a recipe to construct counterexamples as asked for in the second part of the exercise.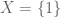 and if
and if 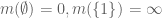 then for any non-negative extended real valued function
then for any non-negative extended real valued function  defined on
defined on  one has
one has 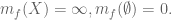
Just notice that (as you suggest) if
Is this correct?