Notational convention: In this post only, I will colour a statement red if it assumes the axiom of choice. (For the rest of the course, the axiom of choice will be implicitly assumed throughout.)
The famous Banach-Tarski paradox asserts that one can take the unit ball in three dimensions, divide it up into finitely many pieces, and then translate and rotate each piece so that their union is now two disjoint unit balls. As a consequence of this paradox, it is not possible to create a finitely additive measure on that is both translation and rotation invariant, which can measure every subset of
, and which gives the unit ball a non-zero measure. This paradox helps explain why Lebesgue measure (which is countably additive and both translation and rotation invariant, and gives the unit ball a non-zero measure) cannot measure every set, instead being restricted to measuring sets that are Lebesgue measurable.
On the other hand, it is not possible to replicate the Banach-Tarski paradox in one or two dimensions; the unit interval in or unit disk in
cannot be rearranged into two unit intervals or two unit disks using only finitely many pieces, translations, and rotations, and indeed there do exist non-trivial finitely additive measures on these spaces. However, it is possible to obtain a Banach-Tarski type paradox in one or two dimensions using countably many such pieces; this rules out the possibility of extending Lebesgue measure to a countably additive translation invariant measure on all subsets of
(or any higher-dimensional space).
In these notes I would like to establish all of the above results, and tie them in with some important concepts and tools in modern group theory, most notably amenability and the ping-pong lemma. This material is not required for the rest of the course, but nevertheless has some independent interest.
— One-dimensional equidecomposability —
Before we study the three-dimensional situation, let us first review the simpler one-dimensional situation. To avoid having to say “X can be cut up into finitely many pieces, which can then be moved around to create Y” all the time, let us make a convenient definition:
Definition 1. (Equidecomposability) Let
be a group acting on a space X, and let A, B be subsets of X.
- We say that A, B are finitely G-equidecomposable if there exist finite partitions
and
and group elements
such that
for all
.
- We say that A, B are countably G-equidecomposable if there exist countable partitions
and
and group elements
such that
for all i.
- We say that A is finitely G-paradoxical if it can be partitioned into two subsets, each of which is finitely G-equidecomposable with A.
- We say that A is countably G-paradoxical if it can be partitioned into two subsets, each of which is countably G-equidecomposable with A.
One can of course make similar definitions when
is an additive group rather than a multiplicative one.
Clearly, finite G-equidecomposability implies countable G-equidecomposability, but the converse is not true. Observe that any finitely (resp. countably) additive and G-invariant measure on X that measures every single subset of X, must give either a zero measure or an infinite measure to a finitely (resp. countably) G-paradoxical set. Thus, paradoxical sets provide significant obstructions to constructing additive measures that can measure all sets.
Example 1. If acts on itself by translation, then
is finitely
-equidecomposable with
, and
is finitely
-equidecomposable with
.
Example 2. If G acts transitively on X, then any two finite subsets of X are finitely -equidecomposable iff they have the same cardinality, and any two countably infinite sets of X are countably
-equidecomposable. In particular, any countably infinite subset of X is countably G-paradoxical.
Exercise 1. Show that finite G-equidecomposability and countable G-equidecomposability are both equivalence relations.
Exercise 2. (Banach-Schroder-Bernstein theorem) Let G act on X, and let A, B be subsets of X.
- If A is finitely G-equidecomposable with a subset of B, and B is finitely G-equidecomposable with a subset of A, show that A and B are finitely G-equidecomposable with each other. (Hint: adapt the proof of the Schroder-Bernstein theorem.)
- If A is finitely G-equidecomposable with a superset of B, and B is finitely G-equidecomposable with a superset of A, show that A and B are finitely G-equidecomposable with each other. (Hint: use part 1.)
- Show that claims 1 and 2 hold when “finitely” is replaced by “countably”.
Exercise 3. Show that if G acts on X, A is a subset of X which is finitely (resp. countably) G-paradoxical, and , then the recurrence set
is also finitely (resp. countably) G-paradoxical (where G acts on itself by translation).
Let us first establish countable equidecomposability paradoxes in the reals.
Proposition 1. Let
act on itself by translations. Then
and
are countably
-equidecomposable.
Proof. By Exercise 2, it will suffice to show that some set contained in is countably
-equidecomposable with
. Consider the space
of all cosets
of the rationals. By the axiom of choice, we can express each such coset as
for some
, thus we can partition
for some
. By Example 2,
is countably
-equidecomposable with
, which implies that
is countably
-equidecomposable with
. Since latter set is
and the former set is contained in [0,1], the claim follows.
Of course, the same proposition holds if [0,1] is replaced by any other interval. As a quick consequence of this proposition and Exercise 2, we see that any subset of containing an interval is
-equidecomposable with
. In particular, we have
Corollary 1. Any subset of
containing an interval is countably
-paradoxical.
In particular, we see that any countably additive translation-invariant measure that measures every subset of , must assign a zero or infinite measure to any set containing an interval. In particular, it is not possible to extend Lebesgue measure to measure all subsets of
.
We now turn from countably paradoxical sets to finitely paradoxical sets. Here, the situation is quite different: we can rule out many sets from being finitely paradoxical. The simplest example is that of a finite set:
Proposition 2. If G acts on X, and A is a non-empty finite subset of X, then A is not finitely (or countably) G-paradoxical.
Proof. One easily sees that any two sets that are finitely or countably G-equidecomposable must have the same cardinality. The claim follows.
Now we consider the integers.
Proposition 3. Let the integers
act on themselves by translation. Then
is not finitely
-paradoxical.
Proof. The integers are of course infinite, and so Proposition 2 does not apply directly. However, the key point is that the integers can be efficiently truncated to be finite, and so we will be able to adapt the Proposition 2 argument in our case.
Let’s see how. Suppose for contradiction that we could partition into two sets A and B, which are in turn partitioned into finitely many pieces
and
, such that
can be partitioned as
and
for some integers
.
Now let N be a large integer (much larger than ). We truncate
to the interval
. Clearly
. (1)
and
. (2)
From (2) we see that the set differs from
by only O(1) elements, where the bound in the O(1) expression can depend on
but does not depend on N. (The point here is that [-N,N] is “almost” translation-invariant in some sense.) Comparing this with (1) we see that
. (3)
Similarly with A replaced by B. Summing, we obtain
, (4)
but this is absurd for N sufficiently large, and the claim follows.
Exercise 4. Use the above argument to show that in fact no infinite subset of is finitely
-paradoxical; combining this with Example 2, we see that the only finitely
-paradoxical set of integers is the empty set.
The above argument can be generalised to an important class of groups:
Definition 2. (Amenability) Let
be a discrete, at most countable, group. A Følner sequence is a sequence
of finite subsets of G with
with the property that
for all
, where
denotes symmetric difference. A discrete, at most countable, group G is amenable if it contains at least one Følner sequence. Of course, one can define the same concept for additive groups
.
Remark 1. One can define amenability for uncountable groups by replacing the notion of a Følner sequence with a Følner net. Similarly, one can define amenability for locally compact Hausdorff groups equipped with a Haar measure by using that measure in place of cardinality in the above definition. However, we will not need these more general notions of amenability here. The notion of amenability was first introduced (though not by this name, or by this definition) by von Neumann, precisely in order to study these sorts of decomposition paradoxes.
Example 3. The sequence for
is a Følner sequence for the integers
, which are hence an amenable group.
Exercise 5. Show that any abelian discrete group that is at most countable, is amenable.
Exercise 6. Show that any amenable discrete group G that is at most countable is not finitely G-paradoxical, when acting on itself. Combined with Exercise 3, we see that if such a group G acts on a non-empty space X, then X is not finitely G-paradoxical.
Remark 2. Exercise 6 suggests that an amenable group G should be able to support a non-trivial finitely additive measure which is invariant under left-translations, and can measure all subsets of G. Indeed, one can even create a finitely additive probability measure, for instance by selecting a non-principal ultrafilter and a Følner sequence
and defining
for all
.
The reals (which we will give the discrete topology!) are uncountable, and thus not amenable by the narrow definition of Definition 2. However, observe from Exercise 5 that any finitely generated subgroup of the reals is amenable (or equivalently, that the reals themselves with the discrete topology are amenable, using the Følner net generalisation of Definition 2). Also, we have the following easy observation:
Exercise 7. Let G act on X, and let A be a subset of X which is finitely G-paradoxical. Show that there exists a finitely generated subgroup H of G such that A is finitely H-paradoxical.
From this, we see that is not finitely
-paradoxical. But we can in fact say much more:
Proposition 4. Let A be a non-empty subset of
. Then A is not finitely
-paradoxical.
Proof. Suppose for contradiction that we can partition A into two sets which are both finitely
-equidecomposable with A. This gives us two maps
,
which are piecewise given by a finite number of translations; thus there exists a finite set
such that
for all
and
.
For any integer , consider the
composition maps
for
. From the disjointness of
and an easy induction we see that the ranges of all these maps are disjoint, and so for any
the
quantities
are distinct. On the other hand, we have
. (5)
Simple combinatorics (relying primarily on the abelian nature of shows that the number of values on the RHS of (5) is at most
. But for sufficiently large N, we have
, giving the desired contradiction.
Let us call a group G supramenable if every non-empty subset of G is not finitely G-paradoxical; thus is supramenable. From Exercise 3 we see that if a supramenable group acts on any space X, then the only finitely G-paradoxical subset of X is the empty set.
Exercise 8. We say that a group has subexponential growth if for any finite subset S of G, we have
, where
is the set of n-fold products of elements of S. Show that every group of subexponential growth is supramenable.
Exercise 9. Show that every abelian group has subexponential growth (and is thus supramenable. More generally, show that every nilpotent group has subexponential growth and is thus also supramenable.
Exercise 10. Show that if two finite unions of intervals in are finitely
-equidecomposable, then they must have the same total length. (Hint: reduce to the case when both sets consist of a single interval. First show that the lengths of these intervals cannot differ by more than a factor of two, and then amplify this fact by iteration to conclude the result.)
Remark 3. We already saw that amenable groups G admit finitely additive translation-invariant probability measures that measure all subsets of G (Remark 2 can be extended to the uncountable case); in fact, this turns out to be an equivalent definition of amenability. It turns out that supramenable groups G enjoy a stronger property, namely that given any non-empty set A on G, there exists a finitely additive translation-invariant measure on G that assigns the measure 1 to A; this is basically a deep result of Tarski.
— Two-dimensional equidecomposability —
Now we turn to equidecomposability on the plane . The nature of equidecomposability depends on what group G of symmetries we wish to act on the plane.
Suppose first that we only allow ourselves to translate various sets in the planes, but not to rotate them; thus . As this group is abelian, it is supramenable by Exercise 9, and so any non-empty subset A of the plane will not be finitely
-paradoxical; indeed, by Remark 3, there exists a finitely additive translation-invariant measure that gives A the measure 1. On the other hand, it is easy to adapt Corollary 1 to see that any subset of the plane containing a ball will be countably
-paradoxical.
Now suppose we allow both translations and rotations, thus G is now the group of (orientation-preserving) isometries
for
and
, where
denotes the anti-clockwise rotation by
around the origin. This group is no longer abelian, or even nilpotent, so Exercise 9 no longer applies. Indeed, it turns out that G is no longer supramenable. This is a consequence of the following three lemmas:
Lemma 1. Let G be a group which contains a free semigroup on two generators (in other words, there exist group elements
such that all the words involving g and h (but not
or
) are distinct). Then G contains a non-empty finitely G-paradoxical set. In other words, G is not supramenable.
Proof. Let S be the semigroup generated by g and h (i.e. the set of all words formed by g and h, including the empty word (i.e. group identity). Observe that gS and hS are disjoint subsets of S that are clearly G-equidecomposable with S. The claim then follows from Exercise 2.
Lemma 2. (Semigroup ping-pong lemma) Let G act on a space X, let g, h be elements of G, and suppose that there exists a non-empty subset A of X such that gA and hA are disjoint subsets of A. Then g, h generate a free semigroup.
Proof. As in the proof of Proposition 4, we see from induction that for two different words w, w’ generated by g, h, the sets wA and w’A are disjoint, and the claim follows.
Lemma 3. The group
contains a free semigroup on two generators.
Proof. It is convenient to identify with the complex plane
. We set g to be the rotation
for some transcendental phase
be such that
is transcendental (such a phase must exist, since the set of algebraic complex numbers is countable), and let
be the translation
. Observe that g and h act on the set A of polynomials in
with non-negative integer coefficients, and that gA and hA are disjoint. The claim now follows from Lemma 2.
Combining Lemma 1 and Lemma 3 to create a countable, finitely paradoxical subset of , and then letting that set act on a generic point in the plane (noting that each group element in
has at most one fixed point), we obtain
Corollary 2. (Sierpinski-Mazurkiewicz paradox) There exist non-empty finitely
-paradoxical subsets of the plane.
We have seen that the group of rigid motions is not supramenable. Nevertheless, it is still amenable, thanks to the following lemma:
Lemma 4. Suppose one has a short exact sequence
of discrete, at most countable, groups, and suppose one has a choice function
that inverts the projection of G to K (the existence of which follows for instance from the well-orderability of G). If H and K are amenable, then so is G.
Proof. Let and
be Følner sequences for H and K respectively. Let
be a rapidly growing function, and let
be the set
. One easily verifies that this is a Følner sequence for G if f is sufficiently rapidly growing. (Strictly speaking, these
do not necessarily cover G, but this can be achieved by right-translating the
suitably. This can be done without choice because an at most countable set is always well-ordered.)
Exercise 11. Show that any finitely generated solvable group is amenable. More generally, show that any discrete, at most countable, solvable group is amenable.
Exercise 12. Show that any finitely generated subgroup of is amenable. (Hint: use the short exact sequence
, which shows that
is solvable (in fact it is metabelian)). Conclude that
is not finitely
-paradoxical.
Finally, we show a result of Banach.
Proposition 5. The unit disk D in
is not finitely
-paradoxical.
Proof. If the claim failed, then D would be finitely -equidecomposable with a disjoint union of two copies of D, say D and D+v for some vector v of length greater than 2. By Exercise 7, we can then find a subgroup G of
generated by a finite number of rotations
for
and translations
for
such that D and
are finitely G-equidecomposable. Indeed, we may assume that the rigid motions that move pieces of D to pieces of
are of the form
for some
, thus
(6)
for some partition of the disk. By incrementing
if necessary we may assume that
is one of the
.
By amenability of the rotation group SO(2), one can find a finite set of rotations such that
differs from
by at most
elements for all
. Let N be a large integer, and let
be the set of all linear combinations of
for
and
with coefficients in
. Observe that
is a finite set whose cardinality grows at most polynomially in N. Thus, by the pigeonhole principle, one can find arbitrarily large N such that
. (7)
On the other hand, from (6) and the rotation-invariance of the disk we have
(8)
for all . Averaging this over all
we conclude
(9)
contradicting (7).
Remark 4. Banach in fact showed the slightly stronger statement that any two finite unions of polygons of differing area were not finitely -equidecomposable. (The converse is also true, and is known as the Bolyai-Gerwien theorem.)
Exercise 13. Show that all the claims in this section continue to hold if we replace by the slightly larger group
of isometries (not necessarily orientation-preserving.
Remark 5. As a consequence of Remark 4, the unit square is not -paradoxical. However, it is
-paradoxical; this is known as the von Neumann paradox.
— Three-dimensional equidecomposability —
We now turn to the three-dimensional setting. The new feature here is that the group of rigid motions is no longer abelian (as in one dimension) or solvable (as in two dimensions), but now contains a free group on two generators (not just a free semigroup, as per Lemma 3). The significance of this fact comes from
Lemma 5. The free group on two generators is finitely
-paradoxical.
Proof. Let a, b be the two generators of . We can partition
, where
is the collection of reduced words of
that begin with c. From the identities
(8)
we see that is finitely
-equidecomposable with both
and
, and the claim now follows from Exercise 2.
Corollary 3. Suppose that
acts freely on a space X (i.e.
whenever
and
is not the identity). Then X is finitely
-paradoxical.
Proof. Using the axiom of choice, we can partition X as for some subset
of X. The claim now follows from Lemma 5.
Next, we embed the free group inside the rotation group SO(3) using the following useful lemma (cf. Lemma 2).
Exercise 14 (ping-pong lemma). Let G act on a set X. Suppose that there exist disjoint subsets of X, whose union is not all of X, and elements
, such that
. (9)
Then a, b generate a free group. (If drawn correctly, a diagram of the inclusions (9) resembles a game of doubles ping-pong of versus
, hence the name.)
Proposition 6.
contains a copy of the free group on two generators.
Proof. It suffices to find a space X that two elements of act on in a way that Exercise 14 applies. There are many such constructions. One is given (and motivated) in this blog post of David Speyer, based on passing from the reals to the 5-adics, where -1 is a square root and so SO(3) becomes isomorphic to PSL(2). At the end of the day, one takes
and
(11)
,
where denotes the integer powers of 5 (which act on column vectors in the obvious manner). The verification of the ping-pong inclusions (9) is a routine application of modular arithmetic.
Remark 6. This is a special case of the Tits alternative.
Corollary 4. (Hausdorff paradox) There exists a countable subset E of the sphere
such that
is finitely
-paradoxical, where
of course acts on
by rotations.
Proof. Let be a copy of the free group on two generators, as given by Proposition 6. Each rotation in
fixes exactly two points on the sphere. Let E be the union of all these points; this is countable since
is countable. The action of
on
is free, and the claim now follows from Corollary 3.
Corollary 5. (Banach-Tarski paradox on the sphere)
is finitely
-paradoxical.
Proof. (Sketch) Iterating the Hausdorff paradox, we see that is finitely
-equidecomposable to four copies of
, which can easily be used to cover two copies of
(with some room to spare), by randomly rotating each of the copies. The claim now follows from Exercise 2.
Exercise 15. (Banach-Tarski paradox on ) Show that the unit ball in
is finitely
-paradoxical.
Exercise 16. Extend these three-dimensional paradoxes to higher dimensions.

48 comments
Comments feed for this article
8 January, 2009 at 1:07 pm
Harald
In exercise 6, do you mean finitely G-paradoxical or countably G-paradoxical?
8 January, 2009 at 1:45 pm
Harald
Also – is it just me, or are your semidirect products SO(n) times R^n pointing in the wrong way? (Surely the triangle bit of the “times” sign should be a “normal subgroup” sign written in the right direction?)
8 January, 2009 at 1:55 pm
Harald
Isn’t a step missing in the proof of Corollary 2? Most elements of the semidirect product R^n ><| SO(n) do have fixed points when they act on R^2 (all rotations do).
8 January, 2009 at 2:26 pm
Terence Tao
Thanks for the corrections!
8 January, 2009 at 5:21 pm
Peter
There’s a stronger version of the Banach-Tarski paradox that was proved recently (by one of my friends) which says that there is a paradoxical decomposition of a sphere in which the pieces move continuously from the original sphere to the two new spheres while remaining disjoint the whole time. The article is pretty short, just 6 pages. BTW, I like the use of red to indicate which things rely on choice, it’s much nicer stylistically than writing “depends on choice” or something like that in each paragraph.
8 January, 2009 at 8:26 pm
Anonymous
While the axiom of choice was used in various places as indicated above, what is known if you are not allowed the axiom of choice? Namely, is it known that there is no Banach-Tarski like result if you do not assume the axiom choice? Perhaps a more concrete question is if you can construct nonmeasurable sets without the axiom choice (I haven’t seen any).
8 January, 2009 at 10:50 pm
Lieven
Solovay proved that ZF + the existence of an inaccessible cardinal + the existence of a Lebesgue measure over all sets of reals is equiconsistent with ZF. Shelah showed later that the use of an inaccessible cardinal is necessary. So in that sense, the use of choice is necessary to “construct” nonmeasurable sets of reals.
9 January, 2009 at 6:39 am
Marlowe, PI
It has been proved that the assertion “every set (in ) is (Lebesgue) measurable” + All other axioms of set theory save for choice is consistent iff the usual theory is consistent. Therefor, if you take out Choice and just keep the other axioms of set theory, you can¿t construct non measurable sets.
) is (Lebesgue) measurable” + All other axioms of set theory save for choice is consistent iff the usual theory is consistent. Therefor, if you take out Choice and just keep the other axioms of set theory, you can¿t construct non measurable sets.
9 January, 2009 at 10:38 am
Anonymous
Less than epsilon, LA
Dear Prof. Tao,
Thank you very much for your excellent blog. It is really helping us too much.
In some research papers and books, Laplace and Fourier transform of measures are used. Could you please explain those concepts and clarify the point which transformation uniquely determines the measure(for finite and infinite case)
thanks
9 January, 2009 at 4:41 pm
Terence Tao
Dear anonymous #1: you might be interested in the related discussion in the comments to Notes 0,
Dear anonymous #2: I plan to discuss this topic when I come to the Stone-Weierstrass theorem, as these sort of unique reconstruction questions are often obtainable directly as consequences of this theorem.
10 January, 2009 at 8:06 am
liuxiaochuan
Dear Professor Tao:
I didn’t quite follow Exercise 10. Are all the intervals with the same length. Could you explain the hint a little more?
Xiaochuan
10 January, 2009 at 8:51 am
Terence Tao
Dear Xiaochuan,
The two unions of intervals can consist of intervals of different lengths, but the exercise is to show that the two unions are equidecomposable if and only if their _total_ lengths are the same. But it is not difficult to see that any finite union of intervals is equidecomposable with a single interval of the same total length, so one can quickly reduce to the case of a single interval.
11 January, 2009 at 1:19 am
liuxiaochuan
Dear Professor Tao:
To make (8) hold, should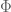 be asked to contain
be asked to contain 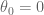 ?
?
Also, is the first equation of (8) correct? And in Prop. 5 and the proof, is actually
actually 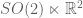 or not?
or not?
Xiaochuan
11 January, 2009 at 8:59 am
Terence Tao
While one can place 0 inside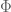 if one wishes, it is not necessary for the proof. There was a factor of 2 missing in the second expression in (8) which has now been corrected, and the direct product should indeed have been a semidirect product.
if one wishes, it is not necessary for the proof. There was a factor of 2 missing in the second expression in (8) which has now been corrected, and the direct product should indeed have been a semidirect product.
13 January, 2009 at 3:12 pm
Anonymous
Anonymous #1 (8 January @ 8:26 pm), the Wikipedia article on the Banach-Tarski paradox has a section about the strength of set theory needed to prove the paradox. You don’t need the full axiom of choice as given in ZFC, but you can’t quite do it in ZF. You can do it with a somewhat weakened version of AC.
28 January, 2009 at 7:16 am
245B, Notes 7: Well-ordered sets, ordinals, and Zorn’s lemma (optional) « What’s new
[…] induction, well-ordered sets, Zorn’s lemma | by Terence Tao Notational convention: As in Notes 2, I will colour a statement red if it assumes the axiom of choice. We will, of course, rely on […]
16 February, 2009 at 7:28 am
实分析0-10 « Liu Xiaochuan’s Weblog
[…] 第二节是全新的内容,我本人没有任何基础,讲的是Banach-Tarski悖论。该悖论是说,一个三维空间的单位球可以被拆成有限个部分,然后仅仅通过平移和旋转,就变成两个单位球。这够令人惊讶的了!但是存在性的证明,并没有具体给出如何拆的方法。而且一步步的看到最后,多少有点被绕糊涂了,没有整体的感觉,有兴趣的恐怕还的看看原始论文了。这篇帖子做了一个很不错的尝试,将所有跟选择公理有关的文字用红色表达。后来有些帖子涉及选择公理比较多的,也是这般处理的。此帖子中我还发现了一个很不多的博客,是由berkeley的几个博士生和博士们合写的。名字叫做Secret Blogging Seminar,叫做SB讨论班,链接在这里。本节中用到的关于将一个自由群嵌入到一个李群中去的方法,那个博客中有一个更清楚的帖子,做了更详细的阐述,我还没来得及细看。 […]
14 April, 2009 at 9:36 pm
Some notes on amenability « What’s new
[…] Remark 2 The non-amenability of the free group is related to the Banach-Tarski paradox (see my earlier lecture notes on […]
19 March, 2010 at 9:54 pm
A computational perspective on set theory « What’s new
[…] dimensional cases is that the free group is not amenable, whereas is amenable. See these previous blog posts for further discussion.) Possibly related posts: (automatically generated)The “no […]
16 April, 2010 at 1:21 pm
Phobos99
Hi, I was wondering if somebody knows a book or a paper that contais the proof of Proposition 1, because I’d like to quote it in my own work and I don’t like quoting a web page.
Thanks,
Phobos99
17 April, 2010 at 11:46 pm
Terence Tao
I believe the result goes back to Vitali; see http://en.wikipedia.org/wiki/Vitali_set
18 April, 2010 at 8:38 am
Phobos99
Thanks for a reply, bud I already knew that.) I talked to my advisor and he sees no problem in quoting this web page = problem solved:)
13 June, 2010 at 1:35 pm
Kestutis Cesnavicius
Several typos:
1. In Remark 2 “group G hould be” —> “group G should be”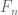 need not cover
need not cover  . If
. If  does not happen to be in the subsequent
does not happen to be in the subsequent 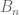 ‘s, the corresponding coset
‘s, the corresponding coset  will not be fully covered.
will not be fully covered.
2. The proof of Lemma 4 needs some additional argument: the sets
3. Proof of Proposition 5: in the 4th line direct product should be semidirect product; same in Remarks 4, 5, and the beginning of the last section.
4. Exercise 13: Isom(R)^2 should be Isom(R^2).
5. Last line of the proof of Lemma 5: c should be b.
15 June, 2010 at 5:52 pm
Terence Tao
Thanks for the corrections! Regarding Lemma 4, this can be fixed by right-translating each of the sets in the Folner sequence to cover the whole space (to do this without choice, one can use the fact that all at most countable sets are well-ordered.)
4 September, 2010 at 10:13 am
245A, prologue: The problem of measure « What’s new
[…] in three dimensions and higher, for reasons having to do with the property of amenability; see this blog post for further discussion of this interesting topic, which is unfortunately too much of a digression […]
26 September, 2010 at 12:32 pm
[Maths]Le lemme de Ping-Pong[*Inachevé] « Yichao's Blog
[…] [ref 3] : https://terrytao.wordpress.com/2009/01/08/245b-notes-2-amenability-the-ping-pong-lemma-and-the-banach… […]
6 October, 2011 at 5:48 am
The Banach-Tarski Paradox « Introduction to Ramsey Theory
[…] Terry Tao’s blog is, as always, a valuable […]
8 July, 2014 at 6:25 pm
Anonymous
Dear Professor Tao, and other readers.
I hope someone will still look at this comment section after all those years. I can’t figure out the 2 inequalities in (8) for Proposition 5. I still don’t understand how they can be derived, and the mysterious role of the N+5. I hope someone can explain this. Thank you.
8 July, 2014 at 9:06 pm
Terence Tao
First hint: One might try first proving the inequalities without the restrictions to the various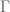 ‘s (ignoring for now the fact that the disks
‘s (ignoring for now the fact that the disks  have infinite cardinality, and focusing on finding the right subset inclusions that give the cardinality bounds), as this is an easier exercise that will guide you for the full problem.
have infinite cardinality, and focusing on finding the right subset inclusions that give the cardinality bounds), as this is an easier exercise that will guide you for the full problem.
It is also worth trying to draw all of the relevant sets to see how they fit together.
More complete solution:
For the first inequality, use the fact that when one translates by
by 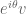 , one gets a new set disjoint from the first, and which is still contained in
, one gets a new set disjoint from the first, and which is still contained in  .
.
For the second inequality, use (6) and the fact that is contained in
is contained in 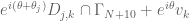 .
.
31 January, 2016 at 2:27 pm
Sebastian
On the second to last paragraph, why is translated by
translated by 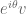 contained in
contained in  ? (I see it is contained in the other rotated copy of the disk, but not the “linear combination of
? (I see it is contained in the other rotated copy of the disk, but not the “linear combination of  ” part) Are we assuming from the get-go that
” part) Are we assuming from the get-go that  for some
for some  (which it seems one could do)?
(which it seems one could do)?
Also, is there a reason for choosing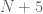 and
and  in the proof instead of
in the proof instead of 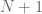 and
and  ? Would that work just as well?
? Would that work just as well?
1 February, 2016 at 8:32 am
Terence Tao
One can certainly replace 5 and 10 here by smaller quantities, but this does not significantly impact the remainder of the argument. It is general practice in mathematics to use round numbers such as 5, 10, or 100 as choices for absolute constants whose exact value is of little importance to the argument.
4 November, 2014 at 8:36 am
Assioma della Scelta e Paradosso di Banach-Tarski | Analisi Matematica 1
[…] che e’ lunga e difficile; il lettore interessato puo’ approfondire l’argomento in questo post (ma servono conoscenze molto piu’ avanzate di quelle del corso di Analisi […]
17 January, 2016 at 8:10 pm
Sebastian
Professor Tao:
Concerning Lemma 4, why does inverting the projection require choice? Couldn’t one well-order G (which is at most countable) and then define by \phi(gH)=min(gH)?
by \phi(gH)=min(gH)?
[Good point; I’ve modified the parenthetical accordingly – T.]
18 January, 2016 at 4:38 am
Anonymous
Well-ordering doesn’t imply the existence of minimums; the set of all integers is well-ordered, but it has infinitely many subsets that don’t have a minimal element.
18 January, 2016 at 7:12 am
Ian
https://en.wikipedia.org/wiki/Well-order
19 January, 2016 at 2:46 am
Anonymous
Oh, right. I forgot that the integers are not well-ordered by the usual order. Maybe the statement of Lemma 4 is slightly wrong; I don’t think G needs to be countable, as long as it’s well-ordered.
19 January, 2016 at 9:13 pm
Ian
Amenability was only defined for at most countable groups.
22 January, 2016 at 7:24 pm
Ian
Wouldn’t exercise 11 have to be modified accordingly as well?
[Fair enough – T.]
25 January, 2016 at 8:51 pm
Yotas Trejos
I’ve been studying this article and I’ve been struggling to understand some of the details in the proofs of Lemma 4 and Proposition 5. I would be very thankful if you could shed some light on this. My doubts are the following:
– In the proof of Lemma 4, I’d had trouble proving that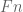 is a Folner sequence, could you please give me some additional hints?
is a Folner sequence, could you please give me some additional hints?
– In the proof of Proposition 5, I don’t quite understand how (or why) you partition a set using sums of sets.
– How does inequality (7) follow from the Pigeonhole Principle? (I verified it supposing by contradiction that the inequality is eventually false for large enough N, and concluded that the sequence grows exponentially, but this argument doesn’t seem to use the Pigeonhole Principle at all)
Thank you in advance
25 January, 2016 at 9:33 pm
Terence Tao
For Lemma 4, one has to show (roughly speaking) that for fixed , that
, that 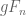 is close to
is close to 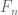 when
when  is large. The point is that for most
is large. The point is that for most  in
in 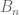 ,
,  still lies in
still lies in 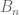 , and for
, and for 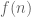 large enough,
large enough,  will be close to
will be close to  . It is an instructive exercise to make the above informal argument rigorous by using epsilons and deltas.
. It is an instructive exercise to make the above informal argument rigorous by using epsilons and deltas.
The sum in Proposition 5 was a typo which has now been corrected.
For (7), one can pigeonhole the quantities , where
, where  ranges over the multiples of 10 between 1 and some large number
ranges over the multiples of 10 between 1 and some large number  , into pigeonholes of the form
, into pigeonholes of the form ![[(1.01)^j, (1.01)^{j+1}]](https://s0.wp.com/latex.php?latex=%5B%281.01%29%5Ej%2C+%281.01%29%5E%7Bj%2B1%7D%5D&bg=ffffff&fg=545454&s=0&c=20201002) , where
, where  ranges up to about
ranges up to about  .
.
7 February, 2016 at 10:08 am
Sebastian
Professor Tao:
Is this argument correct to justify, in Corollary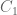 ,
,  of
of  may be used to cover the whole sphere, or is the justification a lot more trivial than this?
may be used to cover the whole sphere, or is the justification a lot more trivial than this?
45, that two copiesThe idea is to leave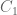 intact and then rotate
intact and then rotate  once to cover the remaining holes. We take as axis of rotation some line
once to cover the remaining holes. We take as axis of rotation some line 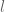 through the origin that has empty intersection with
through the origin that has empty intersection with  . Then, if we project each hole along the great circle passing through the hole and the poles into the maximum circle orthogonal to
. Then, if we project each hole along the great circle passing through the hole and the poles into the maximum circle orthogonal to 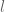 , one sees that the problem is reduced to rotating this newly punctured maximum circle in such a way that every hole is covered. If, say
, one sees that the problem is reduced to rotating this newly punctured maximum circle in such a way that every hole is covered. If, say  is the set of holes, one simply needs to find some angle of rotation
is the set of holes, one simply needs to find some angle of rotation  such that
such that  is disjoint from
is disjoint from  . But if these sets have non-empty intersection, so that
. But if these sets have non-empty intersection, so that  , it follows that
, it follows that 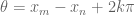 . But the right side of this equation takes countably many values, so we may pick an adequate real number
. But the right side of this equation takes countably many values, so we may pick an adequate real number  .
.
7 February, 2016 at 11:06 am
Ian
You probably meant Corollary 5.
[Corrected – T.]
7 February, 2016 at 4:55 pm
Terence Tao
This will work; one can also rotate and
and  by a random element
by a random element  of the orthogonal group (drawn using Haar measure). For any
of the orthogonal group (drawn using Haar measure). For any  , the probability that
, the probability that  maps
maps 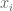 to
to 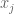 is zero (as this restricts
is zero (as this restricts  to a positive codimension subset of the orthogonal group). Hence by countable additivity, one almost surely has
to a positive codimension subset of the orthogonal group). Hence by countable additivity, one almost surely has  disjoint from
disjoint from  , and so
, and so  and
and 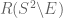 cover
cover 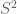 .
.
7 February, 2016 at 5:02 pm
Sebastian
Professor Tao:
The question I posted earlier today seems to have dissappeared, and more importantly your answer (which you seem to have posted recently according to the blog history) is also unreadable.
8 February, 2016 at 11:14 am
Richard
Re broken comments: this appears to be due to the wordpress “paged comments” misfeature. (There is never any reason to ever “page” web content, because “scrolling” has existed long before the web did. Just say no!)
Based on nothing but googling “comment-page-1” and “wordpress”, it may be that turning off “Break comments into pages with XXX top-level comments” in the admin interface /wp-admin/options-discussion.php might do the trick.
Or this might be a new bug in the rotten guts of wordpress.com
[Comments reverted to an unbroken page. (A previous commenter had requested the change due to some pages with 100+ comments being slow to load.) -T.]
24 January, 2018 at 1:49 pm
Maths student
Dear Prof. Tao,
I was not quite sure where to post, or whether this is of any value to you, but while tidying up, I was reading through some things on my to-do list, among them this writeup:
Click to access banach-tarski.pdf
I’m not sure whether the decomposition in the second equation* in the proof of thm. 1.1 holds true, because we e.g. have that the word represents the same group element as the word
represents the same group element as the word  .
.
The argument is of course still correct, and the fix is trivial: One only has to exclude all the elements which occur in both sets from one of the two.
24 January, 2018 at 2:29 pm
Maths student
I see you mean REDUCED words. OK.
7 April, 2022 at 2:58 am
Ahmad Hussein
Dear professor Tao,
In the proof of the Hausdorff paradox, you write: “the action of F2 on SO(3)\E is free”. I think it should be S2\E rather than SO(3)\E. Am I wrong?
Thank you and best regards.
[Corrected, thanks – T.]