One way to study a general class of mathematical objects is to embed them into a more structured class of mathematical objects; for instance, one could study manifolds by embedding them into Euclidean spaces. In these (optional) notes we study two (related) embedding theorems for topological spaces:
- The Stone-Čech compactification, which embeds locally compact Hausdorff spaces into compact Hausdorff spaces in a “universal” fashion; and
- The Urysohn metrization theorem, that shows that every second-countable normal Hausdorff space is metrizable.
— 1. The Stone-Čech compactification —
Observe that any dense open subset of a compact Hausdorff space is automatically a locally compact Hausdorff space. We now study the reverse concept:
Definition 1 A compactification of a locally compact Hausdorff space
is an embedding
(i.e. a homeomorphism between
and
) into a compact Hausdorff space
such that the image
of
is an open dense subset of
. We will often abuse notation and refer to
as the compactification rather than the embedding
, when the embedding is obvious from context.
One compactification
is finer than another
(or
is coarser than
) if there exists a continuous map
such that
; notice that this map must be surjective and unique, by the open dense nature of
. Two compactifications are equivalent if they are both finer than each other.
Example 1 Any compact set can be its own compactification. The real line
can be compactified into
by using the arctan function as the embedding, or (equivalently) by embedding it into the extended real line
. It can also be compactified into the unit circle
by using the stereographic projection
. Notice that the former embedding is finer than the latter. The plane
can similarly be compactified into the unit sphere
by the stereographic projection
.
Exercise 1 Let
be a locally compact Hausdorff space
that is not compact. Define the one-point compactification
by adjoining one point
to
, with the topology generated by the open sets of
, and the complement (in
) of the compact sets in
. Show that
(with the obvious embedding map) is a compactification of
. Show that the one-point compactification is coarser than any other compactification of
.
We now consider the opposite extreme to the one-point compactification:
Definition 2 Let
be a locally compact Hausdorff space. A Stone-Čech compactification
of
is defined as the finest compactification of
, i.e. the compactification of
which is finer than every other compactification of
.
It is clear that the Stone-Čech compactification, if it exists, is unique up to isomorphism, and so one often abuses notation by referring to the Stone-Čech compactification. The existence of the compactification can be established by Zorn’s lemma (see these lecture notes of mine from last year). We shall shortly give several other constructions of the compactification. (All constructions, however, rely at some point on the axiom of choice, or a related axiom.)
The Stone-Čech compactification obeys a useful functorial property:
Exercise 2 Let
be locally compact Hausdorff spaces, with Stone-Čech compactifications
. Show that every continuous map
has a unique continuous extension
. (Hint: uniqueness is easy; for existence, look at the closure of the graph
in
, which compactifies
and thus cannot be strictly finer than
.) In the converse direction, if
is a compactification of
such that every continuous map
into a compact space can be extended continuously to
, show that
is the Stone-Čech compactification.
Example 2 From the above exercise, we can define limits
for any bounded continuous function on
and any
. But one for coarser compactifications, one can only take limits for special types of bounded continuous functions; for instance, using the one-point compactification of
,
need not exist for a bounded continuous function
, e.g.
or
do not exist. The finer the compactification, the more limits can be defined; for instance the two point compactification
of
allows one to define the limits
and
for some additional functions
(e.g.
is well-defined); and the Stone-Čech compactification is the only compactification which allows one to take limits for any bounded continuous function (e.g.
is well-defined for all
).
Now we turn to the issue of actually constructing the Stone-Čech compactifications.
Exercise 3 Let
be a locally compact Hausdorff space. Let
be the space of continuous functions from
to the unit interval, let
be the space of tuples
taking values in the unit interval, with the product topology, and let
be the Gelfand transform
, and let
be the closure of
in
.
- Show that
is a compactification of
. ({\emph Hint}: Use Urysohn’s lemma and Tychonoff’s theorem.)
- Show that
is the Stone-Čech compactification of
. ({\emph Hint}: If
is any other compactification of
, we can identify
as a subset of
, and then project
to
. Meanwhile, we can embed
inside
by the Gelfand transform.)
Exercise 4 Let
be a discrete topological space, let
be the Boolean algebra of all subsets of
. By Stone’s representation theorem (Theorem 1 from Notes 1),
is isomorphic to the clopen algebra of a Stone space
.
- Show that
is a compactification of
.
- Show that
is the Stone-Čech compactification of
.
- Identify
with the space of ultrafilters on
. (See this post for further discussion of ultrafilters, and this post for further discussion of the relationship of ultrafilters to the Stone-Čech compactification.)
Exercise 5 Let
be a locally compact Hausdorff space, and let
be the space of bounded continuous complex-valued functions on
.
- Show that
is a unital commutative
-algebra (see Section 4 of Notes 12).
- By the commutative Gelfand-Naimark theorem (Theorem 14 of Notes 12),
is isomorphic as a unital
-algebra to
for some compact Hausdorff space
(which is in fact the spectrum of
. Show that
is the Stone-Čech compactification of
.
- More generally, show that given any other compactification
of
, that
is isomorphic as a unital
-algebra to a subalgebra of
that contains
(the space of continuous functions from
to
that converge to a limit at
), with
as the spectrum of this algebra; thus we have a canonical identification between compactifications and
-algebras between
and
, which correspond to the Stone-Čech compactification and one-point compactification respectively.
Exercise 6 Let
be a locally compact Hausdorff space. Show that the dual
of
is isomorphic as a Banach space to the space
of real signed Radon measures on the Stone-Čech compactification
, and similarly in the complex case. In particular, conclude that
.
Remark 1 The Stone-Čech compactification can be extended from locally compact Hausdorff spaces to the slightly larger class of Tychonoff spaces, which are those Hausdorff spaces
with the property that any closed set
and point
not in
can be separated by a continuous function
which equals
on
and zero on
. This compactification can be constructed by a modification of the argument used to establish Exercise 3. However, in this case the space
is merely dense in its compactification
, rather than open and dense.
Remark 2 A cautionary note: in general, the Stone-Čech compactification is almost never sequentially compact. For instance, it is not hard to show that
is sequentially closed in
. In particular, these compactifications are usually not metrisable.
— 2. Urysohn’s metrisation theorem —
Recall that a topological space is metrisable if there exists a metric on that space which generates the topology. There are various necessary conditions for metrisability. For instance, we have seen that metric spaces must be normal and Hausdorff. In the converse direction, we have
Theorem 3 (Urysohn’s metrisation theorem) Let
be a normal Hausdorff space which is second countable. Then
is metrisable.
Proof: (Sketch) This will be a variant of the argument in Exercise 3, but with a countable family of continuous functions in place of .
Let be a countable base for
. If
are in this base with
, we can apply Urysohn’s lemma and find a continuous function
which equals
on
and vanishes outside of
. Let
be the collection of all such functions; this is a countable family. We can then embed
in
using the Gelfand transform
. By modifying the proof of Exercise 3 one can show that this is an embedding. On the other hand,
is a countable product of metric spaces and is thus metrisable (e.g. by enumerating
as
and using the metric
). Since a subspace of a metrisable space is clearly also metrisable, the claim follows.
Recalling that compact metric spaces are second countable (Lemma 4 of Notes 10), thus we have
Corollary 4 A compact Hausdorff space is metrisable if and only if it is second countable.
Of course, non-metrisable compact Hausdorff spaces exist; is a standard example. Uncountable products of non-trivial compact metric spaces, such as
, are always non-metrisable. Indeed, we already saw in Notes 10 that
is compact but not sequentially compact (and thus not metrisable) when
has the cardinality of the continuum; one can use the first uncountable ordinal to achieve a similar result for any uncountable
, and then by embedding one can obtain non-metrisability for any uncountable product of non-trivial compact metric spaces, thus complementing the metrisability of countable products of such spaces. Conversely, there also exist metrisable spaces which are not second countable (e.g. uncountable discrete spaces). So Urysohn’s metrisation theorem does not completely classify the metrisable spaces, however it already covers a large number of interesting cases.

28 comments
Comments feed for this article
19 March, 2009 at 1:03 am
javier
With respect to Exercise 5, the algebra of functions of the Stone-Čech compactification admits a concrete realization by means of the original algebra of functions alone. The algebra of functions on corresponds to the so-called “multiplier algebra” of the algebra of functions on
corresponds to the so-called “multiplier algebra” of the algebra of functions on  . From an algebraic point of view, for any algebra
. From an algebraic point of view, for any algebra  the multiplier algebra
the multiplier algebra  is characterized as the biggest unital algebra containing
is characterized as the biggest unital algebra containing  as an essential ideal.
as an essential ideal.
There is a brief explanation about the construction of the multiplier algebra and its relation with compactification in the old ARTS blog:
http://www.neverendingbooks.org/ARTS/?p=28
19 March, 2009 at 4:40 am
Eric
To refine Remark 2 a bit, Stone-Cech compactifications (of completely regular spaces) are never metrizable unless the space you started with was already compact and metrizable. In particular, let X be any noncompact metrizable space. Then X is not sequentially compact, so there is some sequence in X with no accumulation point. Thus
in X with no accumulation point. Thus 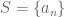 is closed in X and discrete, so by Tietze extension every bounded continuous function on S extends to X. It follows that the induced map
is closed in X and discrete, so by Tietze extension every bounded continuous function on S extends to X. It follows that the induced map 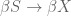 is an embedding, which implies
is an embedding, which implies  is not metrizable (or even sequentially compact) because
is not metrizable (or even sequentially compact) because  is not metrizable.
is not metrizable.
19 March, 2009 at 6:05 am
Mark Meckes
The html for the initial mention of the Urysohn metrization theorem is a bit garbled. [Fixed – T.]
19 March, 2009 at 10:31 am
anon
I don’t understand why the one-point compactification is the coarsest. If we take X = reals, then there is no continuous map X u {oo} = S^1 -> [-1,1] coinciding with the inclusion of X. But there is a unique map the other way round (sent all points in the complement of X in \bar{X} to infinity).
19 March, 2009 at 11:39 am
Anonymous
Could you clarify example 2 by some specific examples?
thanks
19 March, 2009 at 12:34 pm
Anonymous
Dear Prof. Tao,
I am planning to work in the field of PDE. For being a good researcher in this field, which of the following courses you think that a Ph. D. student should take
1-differential geometry
2-operator theory
3-topology
4-fourier analysis
5-harmonic analysis
thanks
19 March, 2009 at 4:53 pm
Matthew Emerton
Dear anon,
“Coarsest” means that all other compactifications map to the one point compactification. So the fact that [-1,1] maps to S^1 exactly shows that
S^1 is coarser than [-1,1] (as it should be).
You can think that giving a compactification means that you complete your space by adding a set of possible “directions at infinity”. In the one point compactification, you add just one point at infinity. (So whichever way you move off to infinity in the space, you always end up at the same point.) The compactification [-1,1] of R has two directions at infinity (one lying at the positive end of the real line, the other at the negative end). In the Stone-Cech compactification, you add all possible directions (in some precise sense).
With this heuristic, “coarse” means there are not many directions at infinity, while “fine” means that there are many. So the one-point compactification is the coarsest, and the Stone-Cech compactification is the finest.
19 March, 2009 at 9:05 pm
anon
That’s what I suspected, but isn’t coarser/finer stated exactly the other way round in Definition 1?
20 March, 2009 at 1:55 am
Terence Tao
Oops, that was reversed; I fixed it now.
21 March, 2009 at 6:25 am
Compactification and Metrisation « memoirs on a rainy day
[…] Compactification and Metrisation Published March 21, 2009 mathematics Tags: Analysis, bolzano weiestrass, compact, compact spaces, mathematics, metric spaces, metrics, terence tao Some great notes from Dr. Terence Tao’s lecture on compacity and metric spaces. […]
21 March, 2009 at 4:09 pm
Paul Leopardi
Thanks for the course notes. In Exercise 3, shouldn’t it say:
… let $\beta X$ be the closure of $\iota X$ in $Q$?
22 March, 2009 at 10:38 am
Pete L. Clark
“Uncountable products of compact metric spaces, such as…are usually non-metrisable also.”
Why not give the precise result?
If {X_i}_{i in I} is a family of nonempty metric spaces, then the product \Pi_i X_i is metrizable if and only if {i in I | # X_i > 1} is a countable set.
(Indeed, if the hypothesis holds, then the space is homeomorphic to a countable product of metrizable spaces so is easy to metrize with an explicit metric. If the hypothesis does not hold, then the product space is not even first countable: Problem 16A, Willard’s _General Topology_.) [Incorporated, thanks, – T.]
23 March, 2009 at 1:10 am
maxbaroi
In exercise 3, I believe it should say that is the closure of
is the closure of  in
in  . [Corrected, thanks, T.]
. [Corrected, thanks, T.]
29 March, 2009 at 1:26 am
The discussion of real analysis: 0 « Liu Xiaochuan’s Weblog
[…] would like start our first disscusion about this post, with the title ‘Compactification and metrisation (optional)’, which is also the last post of another […]
31 March, 2009 at 1:30 am
liuxiaochuan
Dear Professor Tao:
In exercise 3, how to prove the fact that X is open in and the situation in Remark 1 is different, I can’t work it out.
and the situation in Remark 1 is different, I can’t work it out.
31 March, 2009 at 4:34 am
Terence Tao
Dear liuxiaochuan,
If x is in X, and X is LCH, then there exists a compactly supported![f: X \to [0,1]](https://s0.wp.com/latex.php?latex=f%3A+X+%5Cto+%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) which is equal to 1 at x. Now look at the open neighbourhood of x in
which is equal to 1 at x. Now look at the open neighbourhood of x in  consisting of those y for which
consisting of those y for which 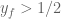 (say). One can show that this neighbourhood is contained entirely inside the compact support of f, and in particular lies in X.
(say). One can show that this neighbourhood is contained entirely inside the compact support of f, and in particular lies in X.
4 April, 2009 at 4:16 pm
245B, Notes 13: Compactification and Metrisation « Less Incompetence
[…] 245B, Notes 13: Compactification and Metrisation Here are some partial solutions to the problems formulated in Notes 13 that can be found here. […]
4 April, 2009 at 4:19 pm
maxbaroi
I just noticed that this doesn’t appear in the 245B category. [Corrected, thanks – T.]
20 January, 2010 at 8:06 am
Seminar „Funktionalanalysis“ « UGroh's Weblog
[…] Stone-Čech-Kompaktifizierung (T. Tao, Compactification and metrisation, Blognotes zur Vorlesung 245B; N. Carothers, l.c. Chap […]
14 March, 2010 at 5:46 am
yangtse
Dear Professor Tao:
In Folland’s Real Analysis 2nd ed. page145, he says that if X is an LCH space, then F={all f in C(X,[0,1]) with compact support} separates points
and closed sets by Urysohn’s lemma. A GLANCE AT the construction of the compactification (Y, e) associated to this F shows that Y consists of e(X) together with the single point of [0,1]^F all of whose coordinates are zero.
How to deduce this conclusion? I mean, how can you show that the closure of e(X) in [0,1]^F has only one point(say, the point of [0,1]^F all of whose coordinates are zero) more than e(X)?
14 March, 2010 at 10:26 am
Terence Tao
This is a good exercise in understanding the weak topology. Start with a point p in [0,1]^F that is not identically zero and not in e(X), and show that (a) there exists a function f in F that separates p from all but a compact set in X, and (b) for every x in that compact set, there exists f in F that separates p from an open neighbourhood of x. Then use compactness.
14 March, 2010 at 6:18 am
a novice
Dear Prof. Tao,
It seems that there is a mistake in the following argument I could not see it.Could you please help me out?
Let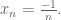 Since it is convergent we know that
Since it is convergent we know that 
Since for every
for every  there exists an
there exists an 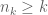 such that
such that 
now, for the above sequence, we should have but that is not correct.
but that is not correct.
Where is my mistake?
thanks
14 March, 2010 at 10:17 am
Terence Tao
The statement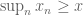 does not mean that there exists n such that
does not mean that there exists n such that 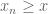 . Instead, it means that for every
. Instead, it means that for every 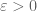 , there exists n such that
, there exists n such that 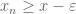 . Thus for instance
. Thus for instance  . Similarly for
. Similarly for  ,
,  , etc.
, etc.
27 April, 2010 at 2:40 pm
crosslegged
I’ve been searching in the literature for an example of a topological space whose Alexandroff compactification is (homeomorphic to) the Stone-Čech compactification — my prof. says he has seen it somewhere, but can’t remember where — do you have any such memory, or ideas?
15 October, 2011 at 10:58 am
254A, Notes 6: Ultraproducts as a bridge between hard analysis and soft analysis « What’s new
[…] to the space . Remark 4 More discussion on the Stone-Cech compactification can be found in this previous blog post. The compact space can also be endowed with an interesting semigroup structure, which is of […]
4 July, 2013 at 10:05 am
What does Kadison-Singer have to do with Quantum Mechanics? | tcs math - some mathematics of theoretical computer science
[…] Indeed, for every partition , a pure -measure can only put non-zero weight on projections involving coordinates of exactly one of or . Furthermore, if then . In other words, for every set of projections, the measure takes only values 0 or 1. Such finitely-additive measures are exactly given by ultrafilters on . The finitely-additive pure -measures are in one-to-one corresponds with such ultrafilters, the set of which can be identified with , the Stone-Cech compactification of the naturals. See Terry Tao’s notes on ultafilters and Stone-Cech compactification. […]
10 April, 2015 at 8:07 am
Matthias Hübner
Dear Prof. Tao,
in Definition 1 right after “One compactification … is finer … if there exists a continuous map …” the arrow should be reversed, or rather domain and codomain swapped. Finer compactifications project/surject onto coarser ones.
And in the following “… such that … notice that this map …” i should be replaced by i’ and vice versa: coarser embedding i’ equals finer embedding i followed by projection pi.
[Corrected, thanks – T.]
3 November, 2019 at 7:36 pm
The Stone-Čech Compactification – Part 3 – Maths to Share
[…] Wikipedia page on the Stone-Čech compactification and these notes by Terrence Tao were where I first learned of the Stone-Čech compactification. I learnt about […]