In set theory, a function is defined as an object that evaluates every input
to exactly one output
. However, in various branches of mathematics, it has become convenient to generalise this classical concept of a function to a more abstract one. For instance, in operator algebras, quantum mechanics, or non-commutative geometry, one often replaces commutative algebras of (real or complex-valued) functions on some space
, such as
or
, with a more general – and possibly non-commutative – algebra (e.g. a
-algebra or a von Neumann algebra). Elements in this more abstract algebra are no longer definable as functions in the classical sense of assigning a single value
to every point
, but one can still define other operations on these “generalised functions” (e.g. one can multiply or take inner products between two such objects).
Generalisations of functions are also very useful in analysis. In our study of spaces, we have already seen one such generalisation, namely the concept of a function defined up to almost everywhere equivalence. Such a function
(or more precisely, an equivalence class of classical functions) cannot be evaluated at any given point
, if that point has measure zero. However, it is still possible to perform algebraic operations on such functions (e.g. multiplying or adding two functions together), and one can also integrate such functions on measurable sets (provided, of course, that the function has some suitable integrability condition). We also know that the
spaces can usually be described via duality, as the dual space of
(except in some endpoint cases, namely when
, or when
and the underlying space is not
-finite).
We have also seen (via the Lebesgue-Radon-Nikodym theorem) that locally integrable functions on, say, the real line
, can be identified with locally finite absolutely continuous measures
on the line, by multiplying Lebesgue measure
by the function
. So another way to generalise the concept of a function is to consider arbitrary locally finite Radon measures
(not necessarily absolutely continuous), such as the Dirac measure
. With this concept of “generalised function”, one can still add and subtract two measures
, and integrate any measure
against a (bounded) measurable set
to obtain a number
, but one cannot evaluate a measure
(or more precisely, the Radon-Nikodym derivative
of that measure) at a single point
, and one also cannot multiply two measures together to obtain another measure. From the Riesz representation theorem, we also know that the space of (finite) Radon measures can be described via duality, as linear functionals on
.
There is an even larger class of generalised functions that is very useful, particularly in linear PDE, namely the space of distributions, say on a Euclidean space . In contrast to Radon measures
, which can be defined by how they “pair up” against continuous, compactly supported test functions
to create numbers
, a distribution
is defined by how it pairs up against a smooth compactly supported function
to create a number
. As the space
of smooth compactly supported functions is smaller than (but dense in) the space
of continuous compactly supported functions (and has a stronger topology), the space of distributions is larger than that of measures. But the space
is closed under more operations than
, and in particular is closed under differential operators (with smooth coefficients). Because of this, the space of distributions is similarly closed under such operations; in particular, one can differentiate a distribution and get another distribution, which is something that is not always possible with measures or
functions. But as measures or functions can be interpreted as distributions, this leads to the notion of a weak derivative for such objects, which makes sense (but only as a distribution) even for functions that are not classically differentiable. Thus the theory of distributions can allow one to rigorously manipulate rough functions “as if” they were smooth, although one must still be careful as some operations on distributions are not well-defined, most notably the operation of multiplying two distributions together. Nevertheless one can use this theory to justify many formal computations involving derivatives, integrals, etc. (including several computations used routinely in physics) that would be difficult to formalise rigorously in a purely classical framework.
If one shrinks the space of distributions slightly, to the space of tempered distributions (which is formed by enlarging dual class to the Schwartz class
), then one obtains closure under another important operation, namely the Fourier transform. This allows one to define various Fourier-analytic operations (e.g. pseudodifferential operators) on such distributions.
Of course, at the end of the day, one is usually not all that interested in distributions in their own right, but would like to be able to use them as a tool to study more classical objects, such as smooth functions. Fortunately, one can recover facts about smooth functions from facts about the (far rougher) space of distributions in a number of ways. For instance, if one convolves a distribution with a smooth, compactly supported function, one gets back a smooth function. This is a particularly useful fact in the theory of constant-coefficient linear partial differential equations such as , as it allows one to recover a smooth solution
from smooth, compactly supported data
by convolving
with a specific distribution
, known as the fundamental solution of
. We will give some examples of this later in these notes.
It is this unusual and useful combination of both being able to pass from classical functions to generalised functions (e.g. by differentiation) and then back from generalised functions to classical functions (e.g. by convolution) that sets the theory of distributions apart from other competing theories of generalised functions, in particular allowing one to justify many formal calculations in PDE and Fourier analysis rigorously with relatively little additional effort. On the other hand, being defined by linear duality, the theory of distributions becomes somewhat less useful when one moves to more nonlinear problems, such as nonlinear PDE. However, they still serve an important supporting role in such problems as a “ambient space” of functions, inside of which one carves out more useful function spaces, such as Sobolev spaces, which we will discuss in the next set of notes.
— 1. Smooth functions with compact support —
In the rest of the notes we will work on a fixed Euclidean space . (One can also define distributions on other domains related to
, such as open subsets of
, or
-dimensional manifolds, but for simplicity we shall restrict attention to Euclidean spaces in these notes.)
A test function is any smooth, compactly supported function ; the space of such functions is denoted
. (In some texts, this space is denoted
instead.)
From analytic continuation one sees that there are no real-analytic test functions other than the zero function. Despite this negative result, test functions actually exist in abundance:
- (i) Show that there exists at least one test function that is not identically zero. (Hint: it suffices to do this for
. One starting point is to use the fact that the function
defined by
for
and
otherwise is smooth, even at the origin
.)
- (ii) Show that if
and
is absolutely integrable and compactly supported, then the convolution
is also in
. (Hint: first show that
is continuously differentiable with
.)
- (iii) (
Urysohn lemma) Let
be a compact subset of
, and let
be an open neighbourhood of
. Show that there exists a function
supported in
which equals
on
. (Hint: use the ordinary Urysohn lemma to find a function in
that equals
on a neighbourhood of
and is supported in a compact subset of
, then convolve this function by a suitable test function.)
- (iv) Show that
is dense in
(in the uniform topology), and dense in
(with the
topology) for all
.
The space is clearly a vector space. Now we place a (very strong!) topology on it. We first observe that
, where
ranges over all compact subsets of
and
consists of those functions
which are supported in
. Each
will be given a topology (called the smooth topology) generated by the norms
for , where we view
as a
-dimensional vector (or, if one wishes, a
-dimensional rank
tensor); thus a sequence
converges to a limit
if and only if
converges uniformly to
for all
. (This gives
the structure of a Fréchet space, though we will not use this fact here.)
We are able to give a (very strong) topology as follows. Call a seminorm
on
good if it is continuous function on
for each compact
(or equivalently, the ball
is open in
for each compact
). We then give
the topology defined by all good seminorms. Clearly, this makes
a (locally convex) topological vector space.
Exercise 2 Let
be a sequence in
, and let
be another function in
. Show that
converges in the topology of
to
if and only if there exists a compact set
such that
are all supported in
, and
converges to
in the smooth topology of
.
Exercise 3
- (i) Show that the topology of
is first countable for every compact
.
- (ii) Show that the topology of
is not first countable. (Hint: given any countable sequence of open neighbourhoods of
, build a new open neighbourhood that does not contain any of the previous ones, using the
-compact nature of
.)
- (iii) As an additional challenge, construct a set
such that
is an adherent point of
, but
is not as the limit of any sequence in
.
There are plenty of continuous operations on :
- (i) Let
be a compact set. Show that a linear map
into a normed vector space
is continuous if and only if there exists
and
such that
for all
.
- (ii) Let
be compact sets. Show that a linear map
is continuous if and only if for every
there exists
and a constant
such that
for all
.
- (iii) Show that a linear map
from the space of test functions into a topological vector space generated by some family of seminorms (i.e., a locally convex topological vector space) is continuous if and only if it is sequentially continuous (i.e. whenever
converges to
in
,
converges to
in
), and if and only if
is continuous for each compact
. Thus while first countability fails for
, we have a serviceable substitute for this property.
- (iv) Show that the inclusion map from
to
is continuous for every
.
- (v) Show that a map
is continuous if and only if for every compact set
there exists a compact set
such that
maps
continuously to
.
- (vi) Show that every linear differential operator with smooth coefficients is a continuous operation on
.
- (vii) Show that convolution with any absolutely integrable, compactly supported function is a continuous operation on
.
- (viii) Show that the product operation
is continuous from
to
.
A sequence of continuous, compactly supported functions is said to be an approximation to the identity if the
are non-negative, have total mass
equal to
, and whose supports shrink to the origin, thus for any fixed
,
is supported on the ball
for
sufficiently large. One can generate such a sequence by starting with a single non-negative continuous compactly supported function
of total mass
, and then setting
; many other constructions are possible also.
One has the following useful fact:
Exercise 5 Let
be a sequence of approximations to the identity.
- (i) If
is continuous, show that
converges uniformly on compact sets to
.
- (ii) If
for some
, show that
converges in
to
. (Hint: use (i), the density of
in
, and Young’s inequality.)
- (iii) If
, show that
converges in
to
. (Hint: use the identity
, cf. Exercise 1(ii).)
Exercise 6 Show that
is separable. (Hint: it suffices to show that
is separable for each compact
. There are several ways to accomplish this. One is to begin with the Stone-Weierstrass theorem, which will give a countable set which is dense in the uniform topology, then use the fundamental theorem of calculus to strengthen the topology. Another is to use Exercise 5 and then discretise the convolution. Another is to embed
into a torus and use Fourier series, noting that the Fourier coefficients
of a smooth function
decay faster than any power of
.)
— 2. Distributions —
Now we can define the concept of a distribution.
Definition 1 (Distribution) A distribution on
is a continuous linear functional
from
to
. The space of such distributions is denoted
, and is given the weak-* topology. In particular, a sequence of distributions
converges (in the sense of distributions) to a limit
if one has
for all
.
A technical point: we endow the space
with the conjugate complex structure. Thus, if
, and
is a complex number, then
is the distribution that maps a test function
to
rather than
; thus
. This is to keep the analogy between the evaluation of a distribution against a function, and the usual Hermitian inner product
of two test functions.
From Exercise 4, we see that a linear functional is a distribution if, for every compact set
, there exists
and
such that
Exercise 7 Show that
is a Hausdorff topological vector space.
We note two basic examples of distributions:
- Any locally integrable function
can be viewed as a distribution, by writing
for all test functions
.
- Any complex Radon measure
can be viewed as a distribution, by writing
, where
is the complex conjugate of
(thus
). (Note that this example generalises the preceding one, which corresponds to the case when
is absolutely continuous with respect to Lebesgue measure.) Thus, for instance, the Dirac measure
at the origin is a distribution, with
for all test functions
.
Exercise 8 Show that the above identifications of locally integrable functions or complex Radon measures with distributions are injective. (Hint: use Exercise 1(iv).)
From the above exercise, we may view locally integrable functions and locally finite measures as a special type of distribution. In particular, and
are now contained in
for all
.
Exercise 9 Show that if a sequence of locally integrable functions converge in
to a limit, then they also converge in the sense of distributions; similarly, if a sequence of complex Radon measures converge in the vague topology to a limit, then they also converge in the sense of distributions.
Thus we see that convergence in the sense of distributions is among the weakest of the notions of convergence used in analysis; however, from the Hausdorff property, distributional limits are still unique.
Exercise 10 If
is a sequence of approximations to the identity, show that
converges in the sense of distributions to the Dirac distribution
.
More exotic examples of distributions can be given:
Exercise 11 (Derivative of the delta function) Let
. Show that the functional
for all test functions
is a distribution which does not arise from either a locally integrable function or a Radon measure. (Note how it is important here that
is smooth (and in particular differentiable, and not merely continuous.) The presence of the minus sign will be explained shortly.
Exercise 12 (Principal value of
) Let
. Show that the functional
defined by the formula
is a distribution which does not arise from either a locally integrable function or a Radon measure. (Note that
is not a locally integrable function!)
Exercise 13 (Distributional interpretations of
) Let
. For any
, show that the functional
defined by the formula
is a distribution that does not arise from either a locally integrable function or a Radon measure. Note that any two such functionals
differ by a constant multiple of the Dirac delta distribution.
Exercise 14 A distribution
is said to be real if
is real for every real-valued test function
. Show that every distribution
can be uniquely expressed as
for some real distributions
.
Exercise 15 A distribution
is said to be non-negative if
is non-negative for every non-negative test function
. Show that a distribution is non-negative if and only if it is a non-negative Radon measure. (Hint: use the Riesz representation theorem and Exercise 1(iv).) Note that this implies that the analogue of the Jordan decomposition fails for distributions; any distribution which is not a Radon measure will not be the difference of non-negative distributions.
We will now extend various operations on locally integrable functions or Radon measures to distributions by arguing by analogy. (Shortly we will give a more formal approach, based on density.)
We begin with the operation of multiplying a distribution by a smooth function
. Observe that
for all test functions . Inspired by this formula, we define the product
of a distribution with a smooth function by setting
for all test functions . It is easy to see (e.g. using Exercise 4(vi)) that this defines a distribution
, and that this operation is compatible with existing definitions of products between a locally integrable function (or Radon measure) with a smooth function. It is important that
is smooth (and not merely, say, continuous) because one needs the product of a test function
with
to still be a test function.
Exercise 16 Let
. Establish the identity
for any smooth function
. In particular,
where we abuse notation slightly and write
for the identity function
. Conversely, if
is a distribution such that
show that
is a constant multiple of
. (Hint: Use the identity
to write
as the sum of
and
times a test function for any test function
, where
is a fixed test function equalling
at the origin.)
Remark 1 Even though distributions are not, strictly speaking, functions, it is often useful heuristically to view them as such, thus for instance one might write a distributional identity such as
suggestively as
. Another useful (and rigorous) way to view such identities is to write distributions such as
as a limit of approximations to the identity
, and show that the relevant identity becomes true in the limit; thus, for instance, to show that
, one can show that
in the sense of distributions as
. (In fact,
converges to zero in the
norm.)
Exercise 17 Let
. With the distribution
from Exercise 12, show that
is equal to
. With the distributions
from Exercise 13, show that
, where
is the signum function.
A distribution is said to be supported in a closed set
in
for all
that vanish on an open neighbourhood of
. The intersection of all
that
is supported on is denoted
and is referred to as the support of the distribution; this is the smallest closed set that
is supported on. Thus, for instance, the Dirac delta function is supported on
, as are all derivatives of that function. (Note here that it is important that
vanish on a neighbourhood of
, rather than merely vanishing on
itself; for instance, in one dimension, there certainly exist test functions
that vanish at
but nevertheless have a non-zero inner product with
.)
Exercise 18 Show that every distribution is the limit of a sequence of compactly supported distributions (using the weak-* topology, of course). (Hint: Approximate a distribution
by the truncated distributions
for some smooth cutoff functions
constructed using Exercise 1(iii).)
In a similar spirit, we can convolve a distribution by an absolutely integrable, compactly supported function
. From Fubini’s theorem we observe the formula
for all test functions , where
. Inspired by this formula, we define the convolution
of a distribution with an absolutely integrable, compactly supported function by the formula
for all test functions . This gives a well-defined distribution
(thanks to Exercise 4(vii)) which is compatible with previous notions of convolution.
Example 1 One has
for all test functions
. In one dimension, we have
(why?), thus differentiation can be viewed as convolution with a distribution.
A remarkable fact about convolutions of two functions is that they inherit the regularity of the smoother of the two factors
(in contrast to products
, which tend to inherit the regularity of the rougher of the two factors). (This disparity can be also be seen by contrasting the identity
with the identity
.) In the case of convolving distributions with test functions, this phenomenon is manifested as follows:
Lemma 2 Let
be a distribution, and let
be a test function. Then
is equal to a smooth function.
Proof: If were itself a smooth function, then one could easily verify the identity
where . As
is a test function, it is easy to see that
varies smoothly in
in any
norm (indeed, it has Taylor expansions to any order in such norms) and so the right-hand side is a smooth function of
. So it suffices to verify the identity (3). As distributions are defined against test functions
, it suffices to show that
On the other hand, we have from (2) that
So the only issue is to justify the interchange of integral and inner product:
Certainly, (from the compact support of ) any Riemann sum can be interchanged with the inner product:
where ranges over some lattice and
is the volume of the fundamental domain. A modification of the argument that shows convergence of the Riemann integral for smooth, compactly supported functions then works here and allows one to take limits; we omit the details.
This has an important corollary:
Lemma 3 Every distribution is the limit of a sequence of test functions. In particular,
is dense in
.
Proof: By Exercise 18, it suffices to verify this for compactly supported distributions . We let
be a sequence of approximations to the identity. By Exercise 5(iii) and (2), we see that
converges in the sense of distributions to
. By Lemma 2,
is a smooth function; as
and
are both compactly supported,
is compactly supported also. The claim follows.
Because of this lemma, we can formalise the previous procedure of extending operations that were previously defined on test functions, to distributions, provided that these operations were continuous in distributional topologies. However, we shall continue to proceed by analogy as it requires fewer verifications in order to motivate the definition.
Exercise 19 Another consequence of Lemma 2 is that it allows one to extend the definition (2) of convolution to the case when
is not an integrable function of compact support, but is instead merely a distribution of compact support. Adopting this convention, show that convolution of distributions of compact support is both commutative and associative. (Hint: this can either be done directly, or by carefully taking limits using Lemma 3.)
The next operation we will introduce is that of differentiation. An integration by parts reveals the identity
for any test functions and
. Inspired by this, we define the (distributional) partial derivative
of a distribution
by the formula
This can be verified to still be a distribution, and by Exercise 4(vi), the operation of differentiation is a continuous one on distributions. More generally, given any linear differential operator with smooth coefficients, one can define
for a distribution
by the formula
where is the adjoint differential operator
, which can be defined implicitly by the formula
for test functions , or more explicitly by replacing all coefficients with complex conjugates, replacing each partial derivative
with its negative, and reversing the order of operations (thus for instance the adjoint of the first-order operator
would be
).
Example 2 The distribution
defined in Exercise 11 is the derivative
of
, as defined by the above formula.
Many of the identities one is used to in classical calculus extend to the distributional setting (as one would already expect from Lemma 3). For instance:
Exercise 20 (Product rule) Let
be a distribution, and let
be smooth. Show that
for all
.
Exercise 21 Let
. Show that
in three different ways:
- Directly from the definitions;
- using the product rule;
- Writing
as the limit of approximations
to the identity.
- (i) Show that if
is a distribution and
is an integer, then
if and only if is a linear combination of
and its first
derivatives
.
- (ii) Show that a distribution
is supported on
if and only if it is a linear combination of
and finitely many of its derivatives.
- (iii) Generalise (ii) to the case of general dimension
(where of course one now uses partial derivatives instead of derivatives).
Exercise 23 Let
.
- Show that the derivative of the Heaviside function
is equal to
.
- Show that the derivative of the signum function
is equal to
.
- Show that the derivative of the locally integrable function
is equal to
.
- Show that the derivative of the locally integrable function
is equal to the distribution
from Exercise 13.
- Show that the derivative of the locally integrable function
is the locally integrable function
.
If a locally integrable function has a distributional derivative which is also a locally integrable function, we refer to the latter as the weak derivative of the former. Thus, for instance, the weak derivative of is
(as one would expect), but
does not have a weak derivative (despite being (classically) differentiable almost everywhere), because the distributional derivative
of this function is not itself a locally integrable function. Thus weak derivatives differ in some respects from their classical counterparts, though of course the two concepts agree for smooth functions.
Exercise 24 Let
. Show that for any
, and any distribution
, we have
, thus weak derivatives commute with each other. (This is in contrast to classical derivatives, which can fail to commute for non-smooth functions; for instance,
at the origin
, despite both derivatives being defined. More generally, weak derivatives tend to be less pathological than classical derivatives, but of course the downside is that weak derivatives do not always have a classical interpretation as a limit of a Newton quotient.)
Exercise 25 Let
, and let
be an integer. Let us say that a compactly supported distribution
has of order at most
if the functional
is continuous in the
norm. Thus, for instance,
has order at most
, and
has order at most
, and every compactly supported distribution is of order at most
for some sufficiently large
.
- Show that if
is a compactly supported distribution of order at most
, then it is a compactly supported Radon measure.
- Show that if
is a compactly supported distribution of order at most
, then
has order at most
.
- Conversely, if
is a compactly supported distribution of order
, then we can write
for some compactly supported distributions of order
. (Hint: one has to “dualise” the fundamental theorem of calculus, and then apply smooth cutoffs to recover compact support.)
- Show that every compactly supported distribution can be expressed as a finite linear combination of (distributional) derivatives of compactly supported Radon measures.
- Show that every compactly supported distribution can be expressed as a finite linear combination of (distributional) derivatives of functions in
, for any fixed
.
We now set out some other operations on distributions. If we define the translation of a test function
by a shift
by the formula
, then we have
for all test functions , so it is natural to define the translation
of a distribution
by the formula
Next, we consider linear changes of variable.
Exercise 26 (Linear changes of variable) Let
, and let
be a linear transformation. Given a distribution
, let
be the distribution given by the formula
for all test functions
. (How would one motivate this formula?)
- Show that
for all linear transformations
.
- If
, show that
for all linear transformations
.
- Conversely, if
and
is a distribution such that
for all linear transformations
. (Hint: first show that there exists a constant
such that
whenever
is a bump function supported in
. To show this, approximate
by the function
for
an approximation to the identity.)
Remark 2 One can also compose distributions with diffeomorphisms. However, things become much more delicate if the map one is composing with contains stationary points; for instance, in one dimension, one cannot meaningfully make sense of
(the composition of the Dirac delta distribution with
); this can be seen by first noting that for an approximation
to the identity,
does not converge to a limit in the distributional sense.
Exercise 27 (Tensor product of distributions) Let
be integers. If
and
are distributions, show that there is a unique distribution
with the property that
for all test functions
,
, where
is the tensor product
of
and
. (Hint: like many other constructions of tensor products, this is rather intricate. One way is to start by fixing two cutoff functions
on
respectively, and define
on modulated test functions
for various frequencies
, and then use Fourier series to define
on
for smooth
. Then show that these definitions of
are compatible for different choices of
and can be glued together to form a distribution; finally, go back and verify (4).)
We close this section with one caveat. Despite the many operations that one can perform on distributions, there are two types of operations which cannot, in general, be defined on arbitrary distributions (at least while remaining in the class of distributions):
- Nonlinear operations (e.g. taking the absolute value of a distribution); or
- Multiplying a distribution by anything rougher than a smooth function.
Thus, for instance, there is no meaningful way to interpret the square of the Dirac delta function as a distribution. This is perhaps easiest to see using an approximation
to the identity:
converges to
in the sense of distributions, but
does not converge to anything (the integral against a test function that does not vanish at the origin will go to infinity as
). For similar reasons, one cannot meaningfully interpret the absolute value
of the derivative of the delta function. (One also cannot multiply
by
– why?)
Exercise 28 Let
be a normed vector space which contains
as a dense subspace (and such that the inclusion of
to
is continuous). The adjoint (or transpose) of this inclusion map is then an injection from
to the space of distributions
; thus
can be viewed as a subspace of the space of distributions.
- Show that the closed unit ball in
is also closed in the space of distributions.
- Conclude that any distributional limit of a bounded sequence in
for
, is still in
.
- Show that the previous claim fails for
, but holds for the space
of finite measures.
— 3. Tempered distributions —
The list of operations one can define on distributions has one major omission – the Fourier transform . Unfortunately, one cannot easily define the Fourier transform for all distributions. One can see this as follows. From Plancherel’s theorem one has the identity
for test functions , so one would like to define the Fourier transform
of a distribution
by the formula
Unfortunately this does not quite work, because the adjoint Fourier transform of a test function is not a test function, but is instead just a Schwartz function. (Indeed, by Exercise 55 of Notes 2, it is not possible to find a non-trivial test function whose Fourier transform is again a test function.) To address this, we need to work with a slightly smaller space than that of all distributions, namely those of tempered distributions:
Definition 4 (Tempered distributions) A tempered distribution is a continuous linear functional
on the Schwartz space
(with the topology given by Exercise 25 of Notes 2), i.e. an element of
.
Since embeds continuously into
(with a dense image), we see that the space of tempered distributions can be embedded into the space of distributions. However, not every distribution is tempered:
Example 3 The distribution
is not tempered. Indeed, if
is a bump function, observe that the sequence of functions
converges to zero in the Schwartz space topology, but
does not go to zero, and so this distribution does not correspond to a tempered distribution.
On the other hand, distributions which avoid this sort of exponential growth, and instead only grow polynomially, tend to be tempered:
Exercise 29 Show that any Radon measure
which is of polynomial growth in the sense that
for all
and some constants
, where
is the ball of radius
centred at the origin in
, is tempered.
Remark 3 As a zeroth approximation, one can roughly think of “tempered” as being synonymous with “polynomial growth”. However, this is not strictly true: for instance, the (weak) derivative of a function of polynomial growth will still be tempered, but need not be of polynomial growth (for instance, the derivative
of
is a tempered distribution, despite having exponential growth). While one can eventually describe which distributions are tempered by measuring their “growth” in both physical space and in frequency space, we will not do so here.
Most of the operations that preserve the space of distributions, also preserve the space of tempered distributions. For instance:
Exercise 30
- Show that any derivative of a tempered distribution is again a tempered distribution.
- Show that and any convolution of a tempered distribution with a compactly supported distribution is again a tempered distribution.
- Show that if
is a measurable function which is rapidly decreasing in the sense that
is an
function for each
, then a convolution of a tempered distribution with
can be defined, and is again a tempered distribution.
- Show that if
is a smooth function such that
and all its derivatives have at most polynomial growth (thus for each
there exists
such that
for all
) then the product of a tempered distribution with
is again a tempered distribution. Give a counterexample to show that this statement fails if the polynomial growth hypotheses are dropped.
- Show that the translate of a tempered distribution is again a tempered distribution.
But we can now add a new operation to this list using (5): as the Fourier transform maps Schwartz functions continuously to Schwartz functions, it also continuously maps the space of tempered distributions to itself. One can also define the inverse Fourier transform
on tempered distributions in a similar manner.
It is not difficult to extend many of the properties of the Fourier transform from Schwartz functions to distributions. For instance:
Exercise 31 Let
be a tempered distribution, and let
be a Schwartz function.
- (Inversion formula) Show that
.
- (Multiplication intertwines with convolution) Show that
and
.
- (Translation intertwines with modulation) For any
, show that
, where
. Similarly, show that for any
, one has
.
- (Linear transformations) For any invertible linear transformation
, show that
.
- (Differentiation intertwines with polynomial multiplication) For any
, show that
, where
and
is the
coordinate function in physical space and frequency space respectively, and similarly
.
Exercise 32 Let
.
- (Inversion formula) Show that
and
.
- (Orthogonality) Let
be a subspace of
, and let
be Lebesgue measure on
. Show that
is Lebesgue measure on the orthogonal complement
of
. (Note that this generalises the previous exercise.)
- (Poisson summation formula) Let
be the distribution
Show that this is a tempered distribution which is equal to its own Fourier transform.
One can use these properties of tempered distributions to start solving constant-coefficient PDE. We first illustrate this by an ODE example, showing how the formal symbolic calculus for solving such ODE that you may have seen as an undergraduate, can now be (sometimes) justified using tempered distributions.
Exercise 33 Let
, let
be real numbers, and let
be the operator
.
- If
, use the Fourier transform to show that all tempered distribution solutions to the ODE
are of the form
for some constants
.
- If
, show that all tempered distribution solutions to the ODE
are of the form
for some constants
.
Remark 4 More generally, one can solve any homogeneous constant-coefficient ODE using tempered distributions and the Fourier transform so long as the roots of the characteristic polynomial are purely imaginary. In all other cases, solutions can grow exponentially as
or
and so are not tempered. There are other theories of generalised functions that can handle these objects (e.g. hyperfunctions) but we will not discuss them here.
Now we turn to PDE. To illustrate the method, let us focus on solving Poisson’s equation
in , where
is a Schwartz function and
is a distribution, where
is the Laplacian. (In some texts, particularly those using spectral analysis, the Laplacian is occasionally defined instead as
, to make it positive semi-definite, but we will eschew that sign convention here, though of course the theory is only changed in a trivial fashion if one adopts it.)
We first settle the question of uniqueness:
Exercise 34 Let
. Using the Fourier transform, show that the only tempered distributions
which are harmonic (by which we mean that
in the sense of distributions) are the harmonic polynomials. (Hint: use Exercise 22.) Note that this generalises Liouville’s theorem. There are of course many other harmonic functions than the harmonic polynomials, e.g.
, but such functions are not tempered distributions.
From the above exercise, we know that the solution to (6), if tempered, is defined up to harmonic polynomials. To find a solution, we observe that it is enough to find a fundamental solution, i.e. a tempered distribution
solving the equation
Indeed, if one then convolves this equation with the Schwartz function , and uses the identity
(which can either be seen directly, or by using Exercise 31), we see that
will be a tempered distribution solution to (6) (and all the other solutions will equal this solution plus a harmonic polynomial). So, it is enough to locate a fundamental solution
. We can take Fourier transforms and rewrite this equation as
(here we are treating the tempered distribution as a function to emphasise that the dependent variable is now
). It is then natural to propose to solve this equation as
though this may not be the unique solution (for instance, one is free to modify by a multiple of the Dirac delta function, cf. Exercise 16).
A short computation in polar coordinates shows that is locally integrable in dimensions
, so the right-hand side of (7) makes sense. To then compute
explicitly, we have from the distributional inversion formula that
so we now need to figure out what the Fourier transform of a negative power of (or the adjoint Fourier transform of a negative power of
) is.
Let us work formally at first, and consider the problem of computing the Fourier transform of the function in
for some exponent
. A direct attack, based on evaluating the (formal) Fourier integral
does not seem to make much sense (the integral is not absolutely integrable), although a change of variables (or dimensional analysis) heuristic can at least lead to the prediction that the integral (8) should be some multiple of . But which multiple should it be? To continue the formal calculation, we can write the non-integrable function
as an average of integrable functions whose Fourier transforms are already known. There are many such functions that one could use here, but it is natural to use Gaussians, as they have a particularly pleasant Fourier transform, namely
for (see Exercise 42 of Notes 2). To get from Gaussians to
, one can observe that
is invariant under the scaling
for
. Thus, it is natural to average the standard Gaussian
with respect to this scaling, thus producing the function
, then integrate with respect to the multiplicative Haar measure
. A straightforward change of variables then gives the identity
where
is the Gamma function. If we formally take Fourier transforms of this identity, we obtain
Another change of variables shows that
and so we conclude (formally) that
thus solving the problem of what the constant multiple of should be.
Exercise 35 Give a rigorous proof of (9) for
(when both sides are locally integrable) in the sense of distributions. (Hint: basically, one needs to test the entire formal argument against an arbitrary Schwartz function.) The identity (9) can in fact be continued meromorphically in
, but the interpretation of distributions such as
when
is not locally integrable is somewhat complicated (cf. Exercise 12) and will not be discussed here.
Specialising back to the current situation with , and using the standard identities
we see that
and similarly
and so from (7) we see that one choice of the fundamental solution is the Newton potential
leading to an explicit (and rigorously derived) solution
to the Poisson equation (6) in for Schwartz functions
. (This is not quite the only fundamental solution
available; one can add a harmonic polynomial to
, which will end up adding a harmonic polynomial to
, since the convolution of a harmonic polynomial with a Schwartz function is easily seen to still be harmonic.)
Exercise 36 Without using the theory of distributions, give an alternate (and still rigorous) proof that the function
defined in (10) solves (6) in
.
Exercise 37
- Show that for any
, a fundamental solution
to the Poisson equation is given by the locally integrable function
where
is the volume of the unit ball in
dimensions.
- Show that for
, a fundamental solution is given by the locally integrable function
.
- Show that for
, a fundamental solution is given by the locally integrable function
.
This we see that for the Poisson equation,
is a “critical” dimension, requiring a logarithmic correction to the usual formula.
Similar methods can solve other constant coefficient linear PDE. We give some standard examples in the exercises below.
Exercise 38 Let
. Show that a smooth solution
to the heat equation
with initial data
for some Schwartz function
is given by
for
, where
is the heat kernel
(This solution is unique assuming certain smoothness and decay conditions at infinity, but we will not pursue this issue here.)
Exercise 39 Let
. Show that a smooth solution
to the Schrödinger equation
with initial data
for some Schwartz function
is given by
for
, where
is the Schrödinger kernel
and we use the standard branch of the complex logarithm (with cut on the negative real axis) to define
. (Hint: You may wish to investigate the Fourier transform of
, where
is a complex number with positive real part, and then let
approach the imaginary axis.) (The close similarity with the heat kernel is a manifestation of Wick rotation in action. However, from an analytical viewpoint, the two kernels are very different. For instance, the convergence of
to
as
follows in the heat kernel case by the theory of approximations to the identity, whereas the convergence in the Schrödinger case is much more subtle, and is best seen via Fourier analysis.)
Exercise 40 Let
. Show that a smooth solution
to the wave equation
with initial data
for some Schwartz functions
is given by the formula
for
, where
is the distribution
where
is Lebesgue measure on the sphere
, and the derivative
is defined in the Newtonian sense
, with the limit taken in the sense of distributions.
Remark 5 The theory of (tempered) distributions is also highly effective for studying variable coefficient linear PDE, especially if the coefficients are fairly smooth, and particularly if one is primarily interested in the singularities of solutions to such PDE and how they propagate; here the Fourier transform must be augmented with more general transforms of this type, such as Fourier integral operators. A classic reference for this topic is the four volumes of Hörmander’s “The analysis of linear partial differential operators”. For nonlinear PDE, subspaces of the space of distributions, such as Sobolev spaces, tend to be more useful.

171 comments
Comments feed for this article
30 December, 2022 at 5:38 pm
Anonymous
Does one have a nontrivial example of good seminorms on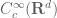 ?
?
[Pretty much all of the standard seminorms are good, e.g., the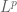 or
or 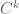 norms. -T.]
norms. -T.]
31 December, 2022 at 7:56 am
Anonymous
In Exercise 11, how to show that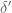 does not arise from a locally integrable function? Suppose
does not arise from a locally integrable function? Suppose  is such that for all test function
is such that for all test function  ,
,
If this is not possible, for any , one can find a text function
, one can find a text function  such that the identity above does not hold. How can one find
such that the identity above does not hold. How can one find  ? Or does one need another approach?
? Or does one need another approach?
31 December, 2022 at 7:58 pm
Terence Tao
Use a sequence of test functions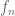 which are uniformly bounded and have uniformly bounded support, but for which
which are uniformly bounded and have uniformly bounded support, but for which 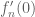 goes to infinity.
goes to infinity.
1 January, 2023 at 5:25 am
Anonymous
… We make the trivial remark that if
Where is the remark used when defining the topology on ?
?
[Oops, this was from an earlier version of the notes; this remark can be safely deleted. -T]
1 January, 2023 at 12:09 pm
Anonymous
If and
and  are two different distributions in
are two different distributions in  . how can one find two disjoint open sets to separate
. how can one find two disjoint open sets to separate  and
and  for showing Hausdorff in Exercise 7? While it is clear to see what convergence in
for showing Hausdorff in Exercise 7? While it is clear to see what convergence in  means from Definition 1, it is unclear how one can construct the desired open sets in the weak* topology.
means from Definition 1, it is unclear how one can construct the desired open sets in the weak* topology.
7 January, 2023 at 7:52 am
Terence Tao
If and
and  are distinct distributions, then there is a test function
are distinct distributions, then there is a test function  such that
such that 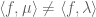 . One can then use the level sets of the linear functional
. One can then use the level sets of the linear functional 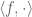 to separate
to separate  and
and  .
.
8 January, 2023 at 4:38 pm
Anonymous
So, since one can separate two real numbers by disjoint intervals and
and  , and the linear functional associated with
, and the linear functional associated with  is continuous, the inverse images of
is continuous, the inverse images of  and
and  under
under 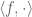 give the open sets separating
give the open sets separating  and
and  .
.
The way a linear functional is used to separate things looks like something very similar to the spirit of the Geometric Hahn-Banach theorem in Notes 6 of 245B. Are there any connections?
11 January, 2023 at 9:27 am
Anonymous
If , can one define the weak derivative as
, can one define the weak derivative as  where the limit is taken as a
where the limit is taken as a 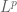 limit? How strong is this one compared to the distributional limit?
limit? How strong is this one compared to the distributional limit?
12 January, 2023 at 9:46 am
Terence Tao
This is basically the Fréchet derivativederivative, and is more restrictive than the weak derivative (if a function is Fréchet differentiable, then it is weakly differentiable and the two derivatives agree, but not every weakly differentiable function will be Fréchet differentiable – you are invited to come up with a counterexample).
18 January, 2023 at 12:39 pm
Anonymous
A minor typo above Exercise 2: is supposed to be
is supposed to be  .
.
12 February, 2023 at 12:10 pm
Anonymous
In Folland’s Real Analysis, the author makes a comment in his book that:
… the definition (of the topology on ) is rather complicated and of little importance for the elementary theory of distributions, so we shall omit it.
) is rather complicated and of little importance for the elementary theory of distributions, so we shall omit it.
In Rudin’s Functional Analysis, Section 6, it is indeed in a rather complicated way:
6.3 Definitions Let be a nonempty open set in
be a nonempty open set in  .
.
(a) For every compact denotes the Fréchet space topology of
denotes the Fréchet space topology of 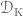 , as described in Sections 1.46 and 6.2.
, as described in Sections 1.46 and 6.2.
(b)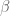 is the collection of all convex balanced sets
is the collection of all convex balanced sets 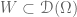 such that
such that  for every compact
for every compact  .
.
(c) is the collection of all unions of sets of the form
is the collection of all unions of sets of the form  , with
, with  and
and 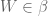 . This will be the topology on
. This will be the topology on  .
.
But in this set of notes, the definition of the topology above Exercise 2 seems rather simple compared to the mentioned ones: all one needs are nothing but the notion of “good” seminorms! Are they all equivalent?
15 February, 2023 at 12:26 pm
Anonymous
Sorry if the question above is unclear. Here is a modified version of the question.
The following is a sketch of how Rudin in his Functional Analysis defines the topology on the space of test functions where
of test functions where  is a nonempty open subset of
is a nonempty open subset of 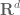 . I am wondering if the special case when
. I am wondering if the special case when  in Rudin gives exactly the same topology as the one in this set of notes. (There are several other definitions on Wikipedia (https://en.wikipedia.org/wiki/Spaces_of_test_functions_and_distributions): none of those looks like the one in this note.)
in Rudin gives exactly the same topology as the one in this set of notes. (There are several other definitions on Wikipedia (https://en.wikipedia.org/wiki/Spaces_of_test_functions_and_distributions): none of those looks like the one in this note.)
– For each compact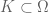 , define
, define  , which is the same as
, which is the same as  in this note.
in this note.
– Define the smooth topology on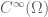 with the seminorms
with the seminorms
where is the union of the compact set
is the union of the compact set 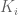 and
and 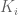 is contained in the interior of
is contained in the interior of 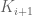 .
.
– is a closed subspace of
is a closed subspace of 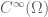 with the smooth topology. (The topology
with the smooth topology. (The topology 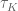 on
on  should be the same as the smooth topology on
should be the same as the smooth topology on  in this note.)
in this note.)
– Let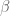 be the set of convex balanced sets
be the set of convex balanced sets 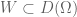 such that
such that  for every compact
for every compact 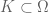 .
.
– The topology on is then defined by sets of the form
is then defined by sets of the form 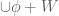 with
with 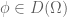 and
and  .
.
4 October, 2023 at 11:03 pm
Anonymous
Hi Prof. Tao,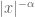 . So what about the Fourier transform of
. So what about the Fourier transform of  with positive
with positive  ? Can we apply the same technique?
? Can we apply the same technique?
Thanks for the wonderful notes. I really admire the procedure for computing the Fourier transform of
[Sure, though the result will be a somewhat exotic distribution, not given as a locally integrable function. -T]