One of the most notorious open problems in functional analysis is the invariant subspace problem for Hilbert spaces, which I will state here as a conjecture:
Conjecture 1 (Invariant Subspace Problem, ISP0) Let
be an infinite dimensional complex Hilbert space, and let
be a bounded linear operator. Then
contains a proper closed invariant subspace
(thus
).
As stated this conjecture is quite infinitary in nature. Just for fun, I set myself the task of trying to find an equivalent reformulation of this conjecture that only involved finite-dimensional spaces and operators. This turned out to be somewhat difficult, but not entirely impossible, if one adopts a sufficiently generous version of “finitary” (cf. my discussion of how to finitise the infinitary pigeonhole principle). Unfortunately, the finitary formulation that I arrived at ended up being rather complicated (in particular, involving the concept of a “barrier”), and did not obviously suggest a path to resolving the conjecture; but it did at least provide some simpler finitary consequences of the conjecture which might be worth focusing on as subproblems.
I should point out that the arguments here are quite “soft” in nature and are not really addressing the heart of the invariant subspace problem; but I think it is still of interest to observe that this problem is not purely an infinitary problem, and does have some non-trivial finitary consequences.
I am indebted to Henry Towsner for many discussions on this topic.
— 1. Initial reductions —
The first reduction is to get rid of the closed invariant subspace , as this will be the most difficult object to finitise. We rephrase ISP0 as
Conjecture 2 (Invariant Subspace Problem, ISP1) Let
be an infinite dimensional complex Hilbert space, and let
be a bounded linear operator. Then there exist unit vectors
such that
for all natural numbers
.
Indeed, to see that ISP1 implies ISP0, we simply take to be the closed invariant subspace generated by the orbit
, which is proper since it is orthogonal to
. To see that ISP0 implies ISP1, we let
be an arbitrary unit vector in the invariant subspace
, and
be an arbitrary unit vector in the orthogonal complement
.
The claim is obvious if is not separable (just let
be arbitrary, and
to be a normal vector to the separable space spanned by
), so we may normalise
to be
. We may also normalise
to be a contraction (thus
), and let
be the coefficients of
.
The next step is to restrict to a compact space of operators. Define a growth function to be a monotone increasing function
. Given any growth function
, we say that a linear contraction
with coefficients
is
-tight if one has the bound
For instance, if the matrix is band-limited to the region
, it is
-tight with
. If it is limited to the region
, then it is
-tight with
. So one can view
-tightness as a weak version of the band-limited property.
The significance of this concept lies in the following lemma:
Lemma 3 (Sequential compactness)
- (i) Every contraction
is
-tight with respect to at least one growth function
.
- (ii) If
is a growth function and
is a sequence of
-tight contractions, then there exists a subsequence
which converges in the strong operator topology to an
-tight contraction
. Furthermore, the adjoints
converge in the strong operator topology to
.
Proof: To prove (i), observe that if is a contraction and
, then
and
and hence by the monotone convergence theorem we can find such that (1), (2). By increasing
as necessary one can make
monotone.
To prove (ii), we apply the usual Arzelá-Ascoli diagonalisation argument to extract a subsequence that converges componentwise (i.e. in the weak operator topology) to a limit
. From Fatou’s lemma we see that
is an
-tight contraction. From the tightness one can upgrade the weak operator topology convergence to strong operator topology convergence (i.e.
for all ) by standard arguments, and similarly for the adjoints.
We will similarly need a way to compactify the unit vectors . If
is a growth function and
are natural numbers, we say that a unit vector
is
-tight if one has
for all , with the convention that
. Similarly, we say that
is
-tight if one has (3) for all
. One has the following variant of Lemma 3:
Lemma 4 (Sequential compactness) Let
be a growth function.
- (i) Every unit vector
is
-tight with respect to at least one increasing sequence
. In fact any finite number of unit vectors
can be made
-tight with the same increasing sequence
.
- (ii) If
, and for each
,
is a
-tight unit vector, then there exists a subsequence
of
that converges strongly to an
-tight unit vector
.
The proof of this lemma is routine and is omitted.
In view of these two lemmas, ISP0 or ISP1 is equivalent to
Conjecture 5 (Invariant Subspace Problem, ISP2) Let
be a growth function, and let
be an
-tight contraction. Then there exist a sequence
and a pair of
-tight unit vectors
such that
for all natural numbers
.
The compactness given by the -tightness and
will be useful for finitising later.
— 2. Finitising —
Now we need a more complicated object.
Definition 6 A barrier is a family
of finite tuples
of increasing natural numbers
, such that
- (i) Every infinite sequence
of natural numbers has at least one initial segment
in
; and
- (ii) If
is a sequence in
, then no initial segment
with
lies in
.
I learned the terminology “barrier” after asking this question on MathOverflow. Examples of barriers include
- The family of all tuples
of increasing natural numbers with
;
- The family of all tuples
of increasing natural numbers with
;
- The family of all tuples
of increasing natural numbers with
.
We now claim that ISP2 is equivalent to the following finitary statement. Let denote the
space on
.
Conjecture 7 (Finitary invariant subspace problem, FISP0) Let
be a growth function, and let
be a barrier. Then there exists a natural number
such that for every
-tight contraction
, there exists a tuple
in
with
, and
-tight unit vectors
, such that
for all
.
We now show that ISP2 and FISP0 are equivalent.
Proof of ISP2 assuming FISP0. Let be a growth function, and let
be an
-tight contraction. Let
denote the set of all tuples
with
such that there does not exist
-tight unit vectors
such that
holds for all
. Let
be those elements of
that contain no proper initial segment in
.
Suppose first that is not a barrier. Then there exists an infinite sequence
such that
for all
, and thus
for all
. In other words, for each
there exists
-tight unit vectors
such that
for all
. By Lemma 4, we can find a subsequence
that converge strongly to
-tight unit vectors
. We conclude that
for all
, and ISP2 follows.
Now suppose instead that is a barrier. Let
be a growth function larger than
to be chosen later. Then the
-tight contraction
is also
-tight, as is the restriction
of
to any finite subspace. Using FISP0, we can thus find
with
and
-tight unit vectors
such that
for all , and in particular for all
. Note that
are almost in
, up to an error of
. From this and the
-tightness of the contraction
, we see (if
is sufficiently rapid) that
and
differ by at most
for
. We conclude that
and so , a contradiction. This yields the proof of ISP2 assuming FISP0.
Proof of FISP0 assuming ISP2. Suppose that FISP0 fails. Then there exists a growth function and a barrier
such that, for every
, there exists an
-tight contraction
such that there does not exist any tuples
in
with
, and
-tight unit vectors
, such that
for all
.
We extend each by zero to an operator on
, which is still a
-tight contraction. Using Lemma 3, one can find a sequence
going to infinity such that
converges in the strong (and dual strong) operator topologies to an
-tight contraction
. Let
be a growth function larger than
to be chosen later. Applying ISP2, there exists an infinite sequence
and
-tight unit vectors
such that
for all
.
As is a barrier, there exists a finite initial segment
of the above sequence that lies in
. For
sufficiently large, we have
, and also we see from the strong operator norm convergence of
to
(and thus
to
for any
, as all operators are uniformly bounded) that
for all .
Now we restrict to
, and then renormalise to create unit vectors
. For
large enough, we have
and we deduce (for large enough) that
are
-tight and
for all
. But this contradicts the construction of the
, and the claim follows.
— 3. A special case —
The simplest example of a barrier is the family of -tuples
, and one of the simplest examples of an
-tight contraction is a contraction that is
-band-limited, i.e. the coefficients
vanish unless
. We thus obtain
Conjecture 8 (Finitary invariant subspace problem, special case, FISP1) Let
be a growth function and
. Then there exists a natural number
such that for every
-band-limited contraction
, there exists
and unit vectors
with
(i.e.
are
-close to
) such that
for all
.
This is perhaps the simplest case of ISP that I do not see how to resolve. (Note that the finite-dimensional operator will have plenty of (generalised) eigenvectors, but there is no particular reason why any of them are “tight” in the sense that they are
-close to
.) Here is a slightly weaker version that I still cannot resolve:
Conjecture 9 (Finitary invariant subspace problem, special case, FISP2) Let
be a growth function, let
, and let
be a
-band-limited contraction. Then there exists
and unit vectors
such that
(i.e.
are
-close to
) such that
for all
.
This claim is implied by ISP but is significantly weaker than it. Informally, it is saying that one can find two reasonably localised vectors , such that the orbit of
is highly orthogonal to
for a very long period of time, much longer than the degree to which
are localised.

24 comments
Comments feed for this article
29 June, 2010 at 1:19 pm
Alon
“(in particular, involving a strange concept which, for want of a better name, ” – and there it breaks. Intriguing!
[Oops, that was a remnant from an earlier draft of the article. Fixed now. -T]
29 June, 2010 at 5:12 pm
Miguel
It is understood that v,w in conjecture 9 are also unit vectors.
[Corrected, thanks – T.]
30 June, 2010 at 4:29 am
Orr
Statement of Lemma 3, “strong operator norm topology”, it seems you mean “strong operator topology”.
[Corrected, thanks – T.]
30 June, 2010 at 5:10 pm
Miguel Lacruz
When you say that conjecture 9 is implied by ISP, you mean that this is so in an elementary way or because it is a special case of FISP0?
1 July, 2010 at 8:42 am
Terence Tao
FISP2 is a consequence of FISP1, which is in turn a consequence of FISP0.
1 July, 2010 at 2:44 pm
Miguel Lacruz
Here is an attempt to apply dilation theory in conjecture 9. The idea is that any contraction on the Hilbert space
on the Hilbert space 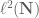 has a unitary power dilation, that is,
has a unitary power dilation, that is, 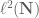 is a subspace of a larger Hilbert space
is a subspace of a larger Hilbert space  and there is a unitary operator
and there is a unitary operator  with the nice property that
with the nice property that  for all
for all 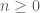 , where
, where 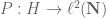 represents the orthogonal projection. This suggests the following modification of conjecture 9:
represents the orthogonal projection. This suggests the following modification of conjecture 9:
Claim A There exists and there are unit vectors
and there are unit vectors 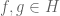 such that
such that
where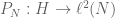 denotes the orthogonal projection.
denotes the orthogonal projection.
Now, consider the vectors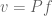 ,
, 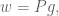 and notice that
and notice that
and therefore
for all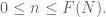 I wonder if this kind of argument can be turned into a proof that FISP2 is a consequence of claim A. Notice that the spectral theorem can be applied to represent the unitary operator
I wonder if this kind of argument can be turned into a proof that FISP2 is a consequence of claim A. Notice that the spectral theorem can be applied to represent the unitary operator  on the Hilbert space
on the Hilbert space  as a multiplication operator, that is,
as a multiplication operator, that is,  where
where 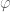 is a measurable function and
is a measurable function and 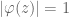 a.e.
a.e.
It is clear that claim A has the following equivalent formulation:
Claim B There exists and there is a function
and there is a function  such that
such that
1 July, 2010 at 4:10 pm
Miguel Lacruz
Sure enough, the function in claim B has norm one.
in claim B has norm one.
2 July, 2010 at 6:41 am
Miguel Lacruz
Claim B should also reflect in the symbol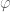 the fact that
the fact that  is a power dilation of a 1-band limited contraction. What can be said about the symbol
is a power dilation of a 1-band limited contraction. What can be said about the symbol  of the minimal unitary power dilation for a 1-band limited contraction?
of the minimal unitary power dilation for a 1-band limited contraction?
4 July, 2010 at 8:21 am
Richard
Terry,
I only read part of this entry, but here goes nuthin’.
Let T: H => H, and let x be in H.
2 3
Consider x, T(x), T (x) [= T(T(x))], T (x), etc.; let V be the subspace of H they generate.
2
If y is in V, then y = a x + a T(x) + a T (x) + … ; then
0 1 2
2
T(y) = T(a x + a T(x) + a T (x) + …)
0 1 2
2 3
= a T(x) + a T (x) + a T (x) + … , which is still in V; so, if y is in V, so is
0 1 2
T(y).
The desired result follows immediately.
2
Take care, T .
— Rich
P.S. When you speak of this comment in the future — and you will — please be kind. (This is, of course, a paraphrase of a famous line from “T and Sympathy”.)
4 July, 2010 at 10:32 am
Miguel Lacruz
oh, come on, rich, you know better than that!
5 July, 2010 at 10:17 am
Richard
Obviously, the subspace I attempted to describe above may => not <= be proper.
Sorry 'bout that.
5 July, 2010 at 6:19 pm
Miguel Lacruz
The operator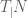 in the proof of ISP2 assuming FISP0 should be called the compression rather than the restriction of
in the proof of ISP2 assuming FISP0 should be called the compression rather than the restriction of  to the subspace
to the subspace 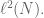 I say this because the subspace
I say this because the subspace  is not necessarily invariant under
is not necessarily invariant under 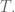
21 July, 2010 at 6:50 am
A New Million Dollar Prize? « Gödel’s Lost Letter and P=NP
[…] have a non-trivial closed invariant sub-space?” See this for some history. See Terence Tao for a recent discussion of this famous […]
13 September, 2010 at 3:27 pm
Miguel Lacruz
Dear Terry,
You stated the invariant subspace problem for operators on Hilbert space as a conjecture. My comment goes as follows: why a conjecture, with such a few examples of Hilbert space operators, ? As a comparison, with a whole lot of numerical evidence, the Riemann hypothesis, is still just a hypothesis. Could you please comment on this?
All my best,
Miguel
13 September, 2010 at 4:28 pm
Terence Tao
Well, as the name suggests, the invariant subspace problem is usually termed a “problem” rather than a “conjecture”, and I think there are opinions in both directions as to what the answer to the problem is. The only reason I called it a conjecture was to be able to talk about the logical relationships between different formulations of that conjecture; it is clear what a statement such as “Conjecture 1 implies Conjecture 2” means, whereas “Problem 1 implies Problem 2” does not make as much sense, because problems are usually not formulated as true-false statements the way a conjecture is.
There is a limit to how much one should read into a name, but I expect that RH is termed a hypothesis due to the immense number of consequences it has. In contrast, I don’t know of many other statements, in functional analysis or otherwise, that would be directly impacted by the solution to the ISP.
14 September, 2010 at 3:32 pm
Miguel Lacruz
Dear Terry,
Thanks for a lot again for your reply, and thanks a lot as well for your clear explanation. Now my comment is the following.
There are a few, but really beautiful results about the existence of invariant subspaces, and they all make very good use of some fixed point theorem. I am thinking about the work of Victor Lomonosov.
I wonder if these results could be reversed to reduce the ISP to, say, a stronger version of Ky Fan’s fixed point theorem. Would that elevate the ISP to the category of the RH?
I ask you please to comment on this.
All my best,
Miguel
27 October, 2010 at 7:00 am
yujiayang
Dear Terry,
In your proof of ISP2 assuming FISP0,
you claim:
(if F’ is sufficiently rapid) the two vectors differ by at most 1/m for 0=< n =1 your hints can’t be used to prove the estimation,unlucky we also can’t find a way to prove your claim.Obviously,it’s a key step for your proof,do you notice this problem?
All my best,
Yu
27 October, 2010 at 8:44 am
Terence Tao
The easiest way to see this is by (sequential) compactness. If the claim was not true, then for every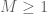 there would exist an F-tight operator
there would exist an F-tight operator 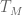 and unit vectors
and unit vectors 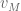 that are within
that are within  of
of  , such that
, such that 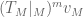 and
and  differ by at least some
differ by at least some 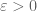 which is independent of
which is independent of  . There is enough compactness here to make
. There is enough compactness here to make 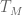 converge to a limit
converge to a limit  in the strong operator topology, and
in the strong operator topology, and 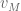 converge to a unit vector
converge to a unit vector  in
in  , after taking a subsequence. But then
, after taking a subsequence. But then 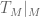 also converges to
also converges to  in the strong operator topology, and so
in the strong operator topology, and so 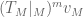 and
and  both converge to
both converge to  , a contradiction.
, a contradiction.
One can also argue directly by carefully choosing one’s epsilons in the right order. The point is that because is strongly localised to
is strongly localised to  (with an accuracy that can be made as strong as one wishes by choosing
(with an accuracy that can be made as strong as one wishes by choosing 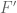 rapid enough) and
rapid enough) and  is
is  -tight, then
-tight, then  is strongly localised to some larger
is strongly localised to some larger  (where
(where 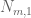 does not depend on
does not depend on 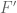 , but rather on
, but rather on 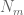 ,
,  , and how strong one wishes the localisation to be). One can then obtain similar localisations for
, and how strong one wishes the localisation to be). One can then obtain similar localisations for  , and this is enough to obtain the desired approximation if
, and this is enough to obtain the desired approximation if 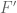 is large enough.
is large enough.
30 October, 2010 at 5:17 am
yujiayang
Dear Terry,
I compute your second suggestion and find that:
Let G(n)=max{F((n+1)^12),n},
if F'(n)>max{G^n(n),16(n+1)^6}for all n in N ( G^n means n composition of G)
then your claim do hold.
Your hint:”T is F-tight, then Tv is strongly localised to some larger L^2(N(m,1)) …” play a key role in this construction.
Thanks for your wise suggestion!
Best wishes!
Yu
26 January, 2013 at 9:30 am
Carnaval Matemáticas: Resuelto el problema del subespacio invariante « Francis (th)E mule Science's News
[…] están bien Terence Tao, “Finitary consequences of the invariant subspace problem,” What’s New, 29 Jun 2010; Adam Azzam, “The Invariant Subspace Problem and Lomonosov’s Theorem,” Part 1, Part […]
26 January, 2013 at 10:46 am
Eva Gallardo y Carl Cowen resuelven el problema del subespacio invariante - Gaussianos
[…] Finitary consequences of the invariant subspace problem en el blog de Terence Tao. […]
12 January, 2014 at 3:36 am
Carnaval Matemáticas: Resuelto el problema del subespacio invariante [erróneamente] | La Ciencia de la Mula Francis
[…] están bien Terence Tao, “Finitary consequences of the invariant subspace problem,” What’s New, 29 Jun 2010; Adam Azzam, “The Invariant Subspace Problem and Lomonosov’s Theorem,” Part 1, Part […]
30 August, 2020 at 9:02 am
SK Rayamajhi
Why is compact operator so prevalent in Invariant subspace problem?
31 August, 2020 at 5:31 pm
Terence Tao
Compact operators are basically those operators that can be well approximated (in various senses) by finite rank operators, and finite-dimensional linear algebra provides plenty of invariant subspaces for finite rank operators. So it is natural to expect that many of the partial results on the invariant subspace problem for finite rank operators can be extended to the compact case. But this still falls well short of the general case, as the class of all bounded operators is much “larger” than the space of compact operators (as witnessed by the complexity of the Calkin algebra).