Let be a finite additive group. A tiling pair is a pair of non-empty subsets
such that every element of
can be written in exactly one way as a sum of an element
of
and an element
of
, in which case we write
. The sets
are then called tiles, with
being a complementary tile to
and vice versa. For instance, every subgroup
of
is a tile, as one can pick one representative from each coset of
to form the complementary tile. Conversely, any set formed by taking one representative from each coset of
is also a tile.
Tiles can be quite complicated, particularly when the group is “high-dimensional”. We will therefore restrict to the simple case of a cyclic group
, and restrict even further to the special case when the modulus
is square-free. Here, the situation should be much simpler. In particular, we have the following conjecture of Coven and Meyerowitz, which asserts that the previous construction of a tile is, in fact, the only such construction:
Conjecture 1 (Coven-Meyerowitz conjecture, square-free case) Let
be square-free, and let
be a tile of
. Then there exists a subgroup
of
such that
consists of a single representative from each coset of
.
Note that in the square-free case, every subgroup of
has a complementary subgroup
(thus
). In particular,
consists of a single representative from each coset of
, and so the examples of subgroups of
are covered by the above conjecture in the square-free case.
In the non-square free case, the above assertion is not true; for instance, if is a prime, then the multiples of
in
are a tile, but cannot be formed from taking a single representative from all the cosets of a given subgroup. There is a more general conjecture of Coven and Meyerowitz to handle this more general case, although it is more difficult to state:
Conjecture 2 (Coven-Meyerowitz conjecture, general case) Let
be a natural number, and let
be a tile of
. Then there exists a set
of prime powers with
such that the Fourier transform
vanishes whenever
is a non-zero element of
whose order is the product of elements of
that are powers of distinct primes. Equivalently, the generating polynomial
is divisible by the cyclotomic polynomials
whenever
is the product of elements of
that are powers of distinct primes.
It can be shown (with a modest amount of effort) that Conjecture 2 implies Conjecture 1, but we will not do so here, focusing instead exclusively on the square-free case for simplicity.
It was observed by Laba that Conjecture 2 is connected to the following well-known conjecture of Fuglede:
Conjecture 3 (One-dimensional Fuglede conjecture, tiling to spectral direction) Let
be a compact subset of
of positive measure which is a tile (thus
for some set
). Then
(with Lebesgue measure) has a spectrum, that is to say an orthogonal set of plane waves
.
Indeed, it was shown by Laba that Conjecture 2 implies Conjecture 3 in the case when is the finite union of unit intervals. Actually, thanks to the more recent work of Farkas, Matolcsi, and Mora we know that Conjecture 2 in fact implies the universal spectrum conjecture of Lagarias and Wang, which in turn was known to imply Conjecture 3 in full generality. (On the other hand, the conjecture fails in four and higher dimensions; see the papers of Kolountzakis-Matolcsi and of Farkas-Revesz.)
Given the simple statement of Conjecture 1, it is perhaps somewhat surprising that it remains open, even in simple cases such as when is the product of just four primes. One reason for this is that some plausible strengthenings of this conjecture (such as the Tijdeman-Sands conjecture) are known to be false, as we will review below. On the other hand, as we shall see, tiling sets have a lot of combinatorial structure, and in principle one should be able to work out a lot of special cases of the conjecture. Given the combinatorial nature of this problem, it may well be quite suitable for a polymath project in fact, if there is sufficient interest.
— 1. Some facts about tiling pairs —
Let be a tiling pair for a cyclic group
of cyclic order. In this section we collect some well-known facts about such pairs, which can be found for instance in the previously cited paper of Coven and Meyerowitz.
The first fact is an obvious cardinality identity:
In particular, and
are divisors of
, and thus are products of disjoint sets of prime factors of
.
The next fact is a physical space separation proeprty
Indeed, if there is a collision between a non-zero difference
of elements of
, and a difference
of elements of
, then one also has a collision
in the sumset
, so that
and
is no longer a tiling pair.
Example 1 If
is a subgroup
, and
is formed by taking a single representative from each coset of
, then
is equal to
, while
can take arbitrary values in
.
In the converse direction, if two non-empty subsets of
obey both (1) and (2), then they must be a tiling pair, since the sums in
are disjoint and have the same cardinality as
.
Now we use Fourier analysis to get more structural information. Observe that the relationship can be rewritten as
and hence (by taking Fourier transforms) as
Note that the case of this identity is again (1). The remaining cases of this identity can be reformulated equivalently as a frequency space separation property
where is the support of
. Conversely, if
obey both (3) and (1), then the above argument shows that
.
Example 2 Continuing Example 1,
is supported on
, while
vanishes on
.
Now we use some basic Galois theory to obtain an important structural control on the Fourier supports. Let us call two elements of
equivalent if one has
for some
coprime to
(or equivalently, if
).
Lemma 4
and
are unions of equivalence classes, with
being the only equivalence class in common.
Proof: By (3) and symmetry, it suffices to show that is the union of equivalence classes. In other words, if
and
is coprime to
, it suffices to show that
if and only if
. But observe that
is an integer polynomial in the
root of unity
, and
is the same polynomial but with
replaced by another primitive
root
of unity. But from the Galois theory of the cyclotomic field
, we know that there is a field automorphism that maps
to
, and so
is non-zero precisely when
is non-zero, and the claim follows.
Remark 1 One can also obtain the above lemma from the theory of cyclotomic polynomials and unique factorisation, noting that the product of the generating polynomials
and
form a multiple of
, and that each cyclotomic polynomial
is irreducible and has zeroes corresponding to a single equivalence class in
.
This feature of Fourier supports has an important corollary:
Corollary 5 (Dilation invariance) Let
for some
. If
is an integer coprime to
, then
, where
is the dilation of
by
.
Proof: From Lemma 4 one has . Since tiling is equivalent to the conditions (1) and (3), the claim follows.
Applying this dilation invariance to the physical space separation property, we conclude
Corollary 6 (Strong physical space separation) The sets
and
lie in disjoint equivalence classes; thus any non-zero equivalence class may contain an element of
or an element of
, but not both.
We can rephrase this corollary in the following more combinatorial way, taking advantage of the square-free hypothesis. We factor the square-free integer as
for some finite set of primes
. By the Chinese remainder theorem, we may then identify
with the Cartesian product
, where
is the cyclic group of order
(but we shall downplay the group structure and often view
simply as a set of
points), which each residue class
being identified with its quotients
. Define a diagonal in
to be a pair
such that
for all
; we say that a subset of
is diagonal-free if it contains no diagonals. Observe that if
contains a diagonal
, then
contains an element
with all coefficients non-zero, or equivalently an invertible element of
. As all invertible elements are equivalent, we conclude from Corollary 6 that at least one of
is diagonal-free. More generally, if
is a non-empty subset of
, define a
-slice of
to be a subset of
of the form
where is a fixed element of
for each
. Thus, for instance, if one has three primes
in
, then
is a subset of
, and a
slice would be a set of the form
for some .
Corollary 7 (Strong physical space separation, combinatorial formulation) Let us view
as subsets of
, and let
be a non-empty subset of
. Then one of the following statements is true:
- All
-slices of
are diagonal-free.
- All
-slices of
are diagonal-free.
Indeed, a diagonal in a -slice of
would create an element of
in the equivalence class of
-tuples whose support was precisely
.
Conversely, we see that any subsets of
with
obeying the conclusion of Corollary 7 will necessarily obey (2) and thus be a tiling pair. Thus we see the rather remarkable fact that the property of being a tiling pair is in fact not dependent on the underlying group structure of
, but only on the Cartesian product structure of
; for instance, one can arbitrarily apply a permutation (or relabeling) of one of the factors
of
to
or
(or both) and still get a tiling pair.
Remark 2 One can make the above independence of the underlying group structure even more striking, as follows. For each prime
in
, let
be an arbitrary quasigroup (or latin square) operation on
, that is to say a binary operation (not assumed to be either commutative or associative) with the property that for each
, the maps
and
are permutations of
. (This quasigroup assumption is of course obeyed by the addition law
on
after identifying
with a cyclic group of order
, but clearly there are also many other quasigroup laws than these.) We can then define a law
in the obvious manner:
The remarkable thing is then that
and
form a tiling pair with respect to the usual addition law
on
if and only if they form a tiling pair with respect to this more general law
, thanks to Corollary 7 and its inverse.
Example 3 Let us partition
, and let
be an element of
. Then one can create a tiling pair by setting
(identifying
with
in the obvious manner), and setting
to consist of a single representative of each slice
for each
. Observe that if
is non-empty and contained in
, then all
-slices of
are diagonal-free; but if
is non-empty and not contained in
, then all
-slices of
are diagonal-free.
Example 4 Suppose
. We consider the sets
and
where
is a constant and
,
, and
are arbitrary functions. One easily verifies that
and
are a tiling pair. If
is a non-empty subset of
, one can check that the
-slices of
are diagonal-free whenever the first element of
is either
or
, and the
-slices of
are diagonal-free whenever the first element of
is either
or
.
One can generalise these sorts of examples to more complicated tiling pairs in general products
, in which each coordinate is free for one of
, and a function of the previous coordinates for the other
.
We isolate one particular instance of Corollary 7: that at least one of or
is a partial graph in any given direction.
Corollary 8 (Graph structure) Let
, and view
as
. Then at least one of
and
is contained in a graph
for some function
.
Indeed, we know that either one of or
obeys the vertical line test, in the sense that its
-slices are diagonal-free (and thus have cardinality at most one).
Now we convert the Fourier-analytic tiling criterion (Lemma 4) into a combinatorial form. We need a definition:
Definition 9 Let
be a product set. A cube in
is a collection of
elements of
of the form
for
, where for each
,
are elements of
. A function
is said to be balanced if the alternating sum of
on any cube vanishes, thus
whenever
for
.
Example 5 If
is a function, then
is balanced if and only if
for all
and
. Equivalently,
takes the form
for some functions
and
.
We have the following equivalent characterisations of balanced functions:
Lemma 10 Let
be the product of cyclic groups, and let
be a function. Then the following are equivalent:
- (i)
is balanced.
- (ii)
is the sum of functions which depend on all but one of the coordinates in
(i.e. they factor through
for some
).
- (iii)
vanishes on the equivalence class
.
Proof: It is easy to see that (ii) implies (i) or (iii), and from the Fourier inversion formula we see that (iii) implies (ii). To see that (i) implies (ii), we apply (4) with (say) to rewrite
in terms of functions that depend on a proper subset of the
.
Combining this with Lemma 4 applied to the equivalence class in the above lemma, we conclude that at least one of and
is balanced. We can also reach the other equivalence classes by projection. Given a subset
of
, let
be the projection map, and given a function
, let
be the pushforward function
Note that the Fourier transform of is essentially the Fourier transform of
restricted to
. From Lemma 4 we conclude that
Corollary 11 (Strong frequency space separation, combinatorial formulation) Let
be a non-empty subset of
. Then at least one of
and
is balanced.
Conversely, if obey the conclusions of (11) and are such that
, then
are a tiling pair.
Example 6 Continuing Example 3,
is balanced whenever
is contained in
, and
is balanced otherwise.
Example 7 Continuing Example 4,
is balanced whenever the largest element of
is
or
, and
is balanced whenever the largest element of
is
or
.
A one-dimensional function is balanced if and only if it is constant. This leads to the following conclusion:
Corollary 12 Let
. Then
is balanced if and only if
divides
, and similarly for
.
Proof: If does not divide
, then
cannot be constant (since it takes integer values on
and has a total
norm of
), and so is not balanced; by Corollary 11, this implies that
is balanced. Since
divides exactly one of
and
, the claim follows.
This already gives a simple case of the Coven-Meyerowitz conjecture:
Proposition 13 The square-free Coven-Meyerowitz conjecture is true when
is a prime.
Proof: Write . Then
is constant on
and has
norm
, and is thus equal to
everywhere. In other words,
meets every coset of
exactly once, and the claim follows.
Corollary 14 The square-free Coven-Meyerowitz conjecture is true when
is the product of at most two primes.
Proof: The claim is trivial when or
, and the only remaining case is covered by Proposition 13.
Remark 3 The paper of Coven-Meyerowitz in fact establishes the general (not necessarily square-free) conjecture when
has at most two distinct prime factors.
— 2. The codimension one case —
Now we give a slightly more difficult case of the conjecture.
Proposition 15 The square-free Coven-Meyerowitz conjecture is true when
is a prime.
We now prove this proposition. We induct on , assuming the claim has been proven for smaller
.
Write , and let
be a tiling complement of
, thus
. As in the proof of Proposition 13,
meets each coset of
exactly once, thus
takes the form
where is a function.
Suppose first that takes values in a proper coset of
(or equivalently, that
takes values in a proper coset of
). Thus
takes values in a translate of
for some
containing
. Then every
-slice of
is essentially a tiling complement of
in
, which among other things implies that
is the product of some primes
in
, and each slice of
then has cardinality
. By the inductive hypothesis, each such slice of
must then consist of one representative from each coset of
in
(note that this is the only subgroup of
that would give the correct cardinality for each slice of
). Gluing the slices together we conclude that
consists of one representative from each coset of
in
as desired. So we may assume that
does not take values in a proper coset of
, and so
does not take values in a proper coset of
. (To put it another way, each component of
is a non-constant function.)
Suppose contains at least one other element than
. Then
is non-constant, so can find
such that
. It is then not difficult to see that one can construct a cube which contains
and no other elements of
except possibly for
. Furthermore, the only time
cannot be avoided is if
and
differ only in the
coordinate. In either case we see that
cannot be balanced. More generally, the same argument shows that
is not balanced for any
containing
and at least one other element, which by Corollary 11 implies that
is balanced for all such
. In other words, the Fourier transform
is supported on
. By the Fourier inversion formula, this implies a decomposition
for some functions ,
and all
,
. But as
only takes the values
or
, we see that at least one of
or
is constant, thus
is either just a function of
or a function of
. In the latter case this would imply that
is a multiple of
, which is absurd since
is square-free; so
must be a function of
; since
, this implies that
is a coset of
and the claim follows.
Corollary 16 The square-free Coven-Meyerowitz conjecture is true when
is the product of at most three primes.
— 3. Slices —
There is an interesting property of the slices of a tiling pair which seems like it should be exploitable further. Pick a prime
in
, and for each
, let
be the slice
of
(identifying
with
in the usual manner). Similarly define
for
.
Proposition 17 (Sums of slices) There exists a partition of
into sets
for
and
for
such that
for all
.
Proof: Since all the sums in are distinct, we see for each
that the sums in
are also distinct, and so
is well-defined. If
are distinct elements of
, and
are distinct elements of
, then from Corollary 7 we see that
and
are disjoint. Thus, for any
, the set
is diagonal-free. But this set also must have cardinality
, since
. Thus, this set is either a vertical line
or a horizontal line
. Letting
denote the set where the former case occurs for a given
, and
the set where the latter case occurs, one obtains the claim.
Here is one small application of the above proposition.
Corollary 18 Suppose the square-free Coven-Meyerowitz conjecture is true for
. Then the square-free Coven-Meyerowitz conjecture is true for any tiling
of
for which at least one of the slices
with
is empty.
Proof: Suppose for instance that is empty. Then by (5), we see that
is empty for all
; thus
is independent of
. As the
are disjoint, this implies that the
are disjoint. Thus, if
, then
for any
. In particular, the
all have the same cardinality. Thus, by hypothesis,
consists of one representative of each coset of some subgroup of
; multiplying this subgroup by
, we conclude that
also meets one representative of each coset of a subgroup of
. Similarly, each of the
consists of one representative of each coset of some subgroup of
; as all the
have the same cardinality and
is square-free, this subgroup must be independent of
. Thus
also consists of exactly one representative of each coset of the same subgroup in
, and the claim follows.
— 4. A counterexample —
In this section we note a counterexample of Szabo to a natural conjecture (due to Sands, with a very similar conjecture also formulated by Tijdeman). In the square-free case, the conjecture reads:
Conjecture 19 (Tijdeman-Sands conjecture) Let
be a tiling of a square-free cyclic group
. Then at least one of
or
is contained in a coset of a proper subgroup of
.
This conjecture would imply the (square-free) Coven-Meyerowitz conjecture, as can be seen from Corollary 18. All the preceding examples of tilings listed previously satisfy this conjecture. However, Szabo showed that this conjecture fails when consists of six primes
. The idea is to start with a base tiling which does not directly counter the conjecture, but then modify it to disprove the conjecture. The base example is given by the sets
and
where ,
,
are arbitrary functions.
It is easy to see that , regardless of what the functions
. Furthermore, if
are chosen to be non-constant, then
is not contained in any proper coset of
. On the other hand,
is clearly contained in a coset of a proper subgroup of
, namely itself. However, this can be remedied by modifying
slightly. If we let
be the line
and be the translated line
then one easily verifies that
In particular, if we remove from
and replace it with
, then the new set obtained is still a tiling complement to
. In a similar spirit, if we let
and
then , and if
and
then . Furthermore,
are disjoint. Thus if we let
be the set
then we see that remains a tiling complement of
. However, it is not difficult to see that unlike
,
is not contained in any coset of a proper subgroup of
.
Remark 4 This construction does not prohibit the weaker conjecture that, given a tiling
, that there is a prime
such that one of the slices
with
is empty; this would still be enough to obtain the Coven-Meyerowitz conjecture, at least in the square-free case.
Remark 5 As noted by Szabo, the same construction also counters a conjecture of Corrádi that if
, then at least one of
or
consists of unions of cosets of a non-trivial subgroup of
.
Remark 6 Curiously, even though Conjecture 19 is false as stated, it is true in a “density” sense. Indeed, from Corollary 7 we know that at least one of
and
is diagonal-free. If say
is diagonal-free, we may translate so that
, and then
is contained in the union of all the “hyperplanes”
through
. If
consists of
primes, then there are
such hyperplanes, so by the pigeonhole principle, one of the hyperplanes contains at least
of the elements of
. Perhaps it may be possible to exploit this sort of observation in the regime where
is bounded and the primes
were large, though I was unable to get any particularly strong control on
or
out of this.
— 5. Some sub-problems —
The full Coven-Meyerowitz conjecture seems difficult, even in the square-free case, but some subproblems seem feasible. For instance:
Problem 20 Is the square-free Coven-Meyerowitz conjecture true when
is the product of four primes,
? In view of Proposition 13 and Proposition 15, one may assume that
and
.
Or:
Problem 21 Suppose we already know that a tile
obeys the square-free Coven-Meyerowitz conjecture (i.e. it consists of one representative of each coset of a subgroup
of
). Does this imply that every tiling complement
of
also obeys the conjecture (replacing
with
, of course?).

10 comments
Comments feed for this article
20 November, 2011 at 5:58 am
Marius Buliga
Re Remark 2, such binary operations are called quasigroup operations. If defined on finite sets then they are also called “latin squares”.
[Remark updated to reflect this terminology, thanks – T.]
4 December, 2011 at 7:28 pm
Ben Wieland
The statement of Lemma 4 is missing some hats.
[Corrected, thanks -T.]
5 December, 2011 at 12:14 am
Aaron Meyerowitz
For conjecture 2 the condition is not quite that rather that
rather that  so a set perhaps
so a set perhaps 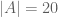 and
and  If I recall correctly (and I need to check), an
If I recall correctly (and I need to check), an  leading to a counterexample has at least 6 prime factors (so the first open cases are
leading to a counterexample has at least 6 prime factors (so the first open cases are  or
or  for square free.)
for square free.)
[Corrected, thanks – T.]
5 December, 2011 at 12:25 pm
ameyerowitz
Thanks for the thoughts. This gives me things to consider.
A few observations:
The conditions address but not
but not  , the conditions can be phrased so that they assume
, the conditions can be phrased so that they assume  is a tile for some unspecified finite cyclic group.
is a tile for some unspecified finite cyclic group.
1) Thus in Conjecture 2 rather than saying vanishes where
vanishes where  has order in
has order in 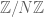 which is a product… one can say
which is a product… one can say  vanishes when
vanishes when  is an integer which is a product …
is an integer which is a product …
2) Corollary 5 remains true if we merely require that is coprime to
is coprime to  (which will of course make it coprime to
(which will of course make it coprime to  .)
.)
I worry that I am missing something but let me put this out there for possible correction:
3) In the event that and
and  is coprime to
is coprime to  (as will certainly be the case when
(as will certainly be the case when  is square-free) we also have
is square-free) we also have  and here
and here  is a subgroup.
is a subgroup.
4) Note that is a tile of
is a tile of 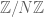 if and only if
if and only if  is a tile of
is a tile of  where
where  and
and  is the largest divisor of
is the largest divisor of  coprime to
coprime to  .
.
5 December, 2011 at 12:41 pm
Terence Tao
Unfortunately I don’t know how to free the proof of Lemma 4 (and hence Corollary 5) from the dependence on N, as one needs coprimality of m and N to get the Galois automorphism of the cyclotomic ring of order N. If one could obtain your conclusion 3), this would immediately resolve Conjecture 1. This does seem to be a nice reformulation of that conjecture, though…
5 December, 2011 at 12:26 pm
ameyerowitz
Sorry, don’t have the hang of this yet and not sure how to delete and fix the latex above. [I repaired the latex; one has to insert the keyword “latex” at the beginning of every math mode fragment, as explained in the bottom left corner of this blog. Unfortunately there is no ability to anyone other than myself to edit comments. -T.]
1 January, 2012 at 12:04 am
Dr Emmanuel Amiot
I am happy to bring to your notice that problem 20 is solved, as is the case . These are two cases when
. These are two cases when  is a Hajos group, and in that case any direct sum decomposition of the cyclic group can be projected on a decomposition of a subgroup. I proved in Amiot, E., Rhythmic canons and Galois theory, Grazer Math. Ber., 347 (2005), 1–25 that condition (T2) is preserved under this operation and the converse (and some others), and hence as (tiling => (T2)) for the subgroups it must be true initially. In more modern times it boils down to expressions of DFT in
is a Hajos group, and in that case any direct sum decomposition of the cyclic group can be projected on a decomposition of a subgroup. I proved in Amiot, E., Rhythmic canons and Galois theory, Grazer Math. Ber., 347 (2005), 1–25 that condition (T2) is preserved under this operation and the converse (and some others), and hence as (tiling => (T2)) for the subgroups it must be true initially. In more modern times it boils down to expressions of DFT in  vs.
vs.  .
.
This kind of transformational process fails with the Szabo counterexamples family, unfortunately. Maybe this is what Aaron had in mind in his first comment.
Some computational progress in that direction has been made since, with fresh ideas from Matolcsi & Koloutzakis, see Journal of Mathematics and Music, Volume 3, Issue 2 July (2009).
9 January, 2012 at 10:16 pm
Izabella Laba
I was just looking at it today. Is there a reason why the argument from Lemma 2.3 in the Coven-Meyerowitz case wouldn’t cover the square-free case? Or am I missing something?
Suppose that with N square-free. Let r be a prime dividing |B|, then r does not divide |A|. By Tijdeman’s theorem,
with N square-free. Let r be a prime dividing |B|, then r does not divide |A|. By Tijdeman’s theorem,  . Let
. Let  , then |B’|=|B|/r (this follows for example because
, then |B’|=|B|/r (this follows for example because  divides B(x), so that B has the same number of elements in each congruence class mod r). Then
divides B(x), so that B has the same number of elements in each congruence class mod r). Then  . Dividing everything by r, we get that
. Dividing everything by r, we get that  , where B”=B’/r and |B”|=N/r.
, where B”=B’/r and |B”|=N/r.
Iterating the procedure with one prime factor of |B| at a time, we eventually get a tiling , so that A = {0,1,…,|A|-1} (mod |A|). In particular, the Coven-Meyerovitz conditions hold for A.
, so that A = {0,1,…,|A|-1} (mod |A|). In particular, the Coven-Meyerovitz conditions hold for A.
The argument doesn’t really seem to require that N be square-free, only that |B| be relatively prime to |A|.
10 January, 2012 at 11:32 am
Terence Tao
Ah, you’re right, this does seem to resolve the square-free case (Conjecture 1). (Aaron already tried to tell me this in an earlier comment, but I somehow missed the point of his remarks.) What had happened was that I had taken the proof of Lemma 3.1 in the Coven-Meyerowitz paper and simplified it to give Lemma 4 above, but the cost of this simplification is that I needed r to be coprime to N and not just to |A|. But you are right, the original argument in Coven-Meyerowitz (or Tijdeman) does seem to work in this case.
2 January, 2024 at 11:35 am
Anonymous
In Example 3, do you mean for to consist of a single representative of
to consist of a single representative of  for each
for each  ?
?
[Corrected, thanks – T.]