A Fourier-free proof of the Furstenberg-Sarkozy theorem

28 February, 2013 in expository, math.CO | Tags: Cauchy-Schwarz, density increment argument, Furstenberg-Sarkozy theorem, van der Corput lemma | by Terence Tao

The following result is due independently to Furstenberg and to Sarkozy:

Theorem 1 (Furstenberg-Sarkozy theorem) Let ${\delta > 0}$ , and suppose that ${N}$ is sufficiently large depending on ${\delta}$ . Then every subset ${A}$ of ${[N] := \{1,\ldots,N\}}$ of density ${|A|/N}$ at least ${\delta}$ contains a pair ${n, n+r^2}$ for some natural numbers ${n, r}$ with ${r \neq 0}$ .

This theorem is of course similar in spirit to results such as Roth’s theorem or Szemerédi’s theorem, in which the pattern ${n,n+r^2}$ is replaced by ${n,n+r,n+2r}$ or ${n,n+r,\ldots,n+(k-1)r}$ for some fixed ${k}$ respectively. There are by now many proofs of this theorem (see this recent paper of Lyall for a survey), but most proofs involve some form of Fourier analysis (or spectral theory). This may be compared with the standard proof of Roth’s theorem, which combines some Fourier analysis with what is now known as the density increment argument.

A few years ago, Ben Green, Tamar Ziegler, and myself observed that it is possible to prove the Furstenberg-Sarkozy theorem by just using the Cauchy-Schwarz inequality (or van der Corput lemma) and the density increment argument, removing all invocations of Fourier analysis, and instead relying on Cauchy-Schwarz to linearise the quadratic shift ${r^2}$ . As such, this theorem can be considered as even more elementary than Roth’s theorem (and its proof can be viewed as a toy model for the proof of Roth’s theorem). We ended up not doing too much with this observation, so decided to share it here.

The first step is to use the density increment argument that goes back to Roth. For any ${\delta > 0}$ , let ${P(\delta)}$ denote the assertion that for ${N}$ sufficiently large, all sets ${A \subset [N]}$ of density at least ${\delta}$ contain a pair ${n,n+r^2}$ with ${r}$ non-zero. Note that ${P(\delta)}$ is vacuously true for ${\delta > 1}$ . We will show that for any ${0 < \delta_0 \leq 1}$ , one has the implication

$\displaystyle P(\delta_0 + c \delta_0^3) \implies P(\delta_0) \ \ \ \ \ (1)$

for some absolute constant ${c>0}$ . This implies that ${P(\delta)}$ is true for any ${\delta>0}$ (as can be seen by considering the infimum of all ${\delta>0}$ for which ${P(\delta)}$ holds), which gives Theorem 1.

It remains to establish the implication (1). Suppose for sake of contradiction that we can find ${0 < \delta_0 \leq 1}$ for which ${P(\delta_0+c\delta^3_0)}$ holds (for some sufficiently small absolute constant ${c>0}$ ), but ${P(\delta_0)}$ fails. Thus, we can find arbitrarily large ${N}$ , and subsets ${A}$ of ${[N]}$ of density at least ${\delta_0}$ , such that ${A}$ contains no patterns of the form ${n,n+r^2}$ with ${r}$ non-zero. In particular, we have

$\displaystyle \mathop{\bf E}_{n \in [N]} \mathop{\bf E}_{r \in [N^{1/3}]} \mathop{\bf E}_{h \in [N^{1/100}]} 1_A(n) 1_A(n+(r+h)^2) = 0.$

(The exact ranges of ${r}$ and ${h}$ are not too important here, and could be replaced by various other small powers of ${N}$ if desired.)

Let ${\delta := |A|/N}$ be the density of ${A}$ , so that ${\delta_0 \leq \delta \leq 1}$ . Observe that

$\displaystyle \mathop{\bf E}_{n \in [N]} \mathop{\bf E}_{r \in [N^{1/3}]} \mathop{\bf E}_{h \in [N^{1/100}]} 1_A(n) \delta 1_{[N]}(n+(r+h)^2) = \delta^2 + O(N^{-1/3})$

$\displaystyle \mathop{\bf E}_{n \in [N]} \mathop{\bf E}_{r \in [N^{1/3}]} \mathop{\bf E}_{h \in [N^{1/100}]} \delta 1_{[N]}(n) \delta 1_{[N]}(n+(r+h)^2) = \delta^2 + O(N^{-1/3})$

and

$\displaystyle \mathop{\bf E}_{n \in [N]} \mathop{\bf E}_{r \in [N^{1/3}]} \mathop{\bf E}_{h \in [N^{1/100}]} \delta 1_{[N]}(n) 1_A(n+(r+h)^2) = \delta^2 + O( N^{-1/3} ).$

If we thus set ${f := 1_A - \delta 1_{[N]}}$ , then

$\displaystyle \mathop{\bf E}_{n \in [N]} \mathop{\bf E}_{r \in [N^{1/3}]} \mathop{\bf E}_{h \in [N^{1/100}]} f(n) f(n+(r+h)^2) = -\delta^2 + O( N^{-1/3} ).$

In particular, for ${N}$ large enough,

$\displaystyle \mathop{\bf E}_{n \in [N]} |f(n)| \mathop{\bf E}_{r \in [N^{1/3}]} |\mathop{\bf E}_{h \in [N^{1/100}]} f(n+(r+h)^2)| \gg \delta^2.$

On the other hand, one easily sees that

$\displaystyle \mathop{\bf E}_{n \in [N]} |f(n)|^2 = O(\delta)$

and hence by the Cauchy-Schwarz inequality

$\displaystyle \mathop{\bf E}_{n \in [N]} \mathop{\bf E}_{r \in [N^{1/3}]} |\mathop{\bf E}_{h \in [N^{1/100}]} f(n+(r+h)^2)|^2 \gg \delta^3$

which we can rearrange as

$\displaystyle |\mathop{\bf E}_{r \in [N^{1/3}]} \mathop{\bf E}_{h,h' \in [N^{1/100}]} \mathop{\bf E}_{n \in [N]} f(n+(r+h)^2) f(n+(r+h')^2)| \gg \delta^3.$

Shifting ${n}$ by ${(r+h)^2}$ we obtain (again for ${N}$ large enough)

$\displaystyle |\mathop{\bf E}_{r \in [N^{1/3}]} \mathop{\bf E}_{h,h' \in [N^{1/100}]} \mathop{\bf E}_{n \in [N]} f(n) f(n+(h'-h)(2r+h'+h))| \gg \delta^3.$

In particular, by the pigeonhole principle (and deleting the diagonal case ${h=h'}$ , which we can do for ${N}$ large enough) we can find distinct ${h,h' \in [N^{1/100}]}$ such that

$\displaystyle |\mathop{\bf E}_{r \in [N^{1/3}]} \mathop{\bf E}_{n \in [N]} f(n) f(n+(h'-h)(2r+h'+h))| \gg \delta^3,$

so in particular

$\displaystyle \mathop{\bf E}_{n \in [N]} |\mathop{\bf E}_{r \in [N^{1/3}]} f(n+(h'-h)(2r+h'+h))| \gg \delta^3.$

If we set ${d := 2(h'-h)}$ and shift ${n}$ by ${(h'-h) (h'+h)}$ , we can simplify this (again for ${N}$ large enough) as

$\displaystyle \mathop{\bf E}_{n \in [N]} |\mathop{\bf E}_{r \in [N^{1/3}]} f(n+dr)| \gg \delta^3. \ \ \ \ \ (2)$

On the other hand, since

$\displaystyle \mathop{\bf E}_{n \in [N]} f(n) = 0$

we have

$\displaystyle \mathop{\bf E}_{n \in [N]} f(n+dr) = O( N^{-2/3+1/100})$

for any ${r \in [N^{1/3}]}$ , and thus

$\displaystyle \mathop{\bf E}_{n \in [N]} \mathop{\bf E}_{r \in [N^{1/3}]} f(n+dr) = O( N^{-2/3+1/100}).$

Averaging this with (2) we conclude that

$\displaystyle \mathop{\bf E}_{n \in [N]} \max( \mathop{\bf E}_{r \in [N^{1/3}]} f(n+dr), 0 ) \gg \delta^3.$

In particular, by the pigeonhole principle we can find ${n \in [N]}$ such that

$\displaystyle \mathop{\bf E}_{r \in [N^{1/3}]} f(n+dr) \gg \delta^3,$

or equivalently ${A}$ has density at least ${\delta+c'\delta^3}$ on the arithmetic progression ${\{ n+dr: r \in [N^{1/3}]\}}$ , which has length ${\lfloor N^{1/3}\rfloor }$ and spacing ${d}$ , for some absolute constant ${c'>0}$ . By partitioning this progression into subprogressions of spacing ${d^2}$ and length ${\lfloor N^{1/4}\rfloor}$ (plus an error set of size ${O(N^{1/4})}$ , we see from the pigeonhole principle that we can find a progression ${\{ n' + d^2 r': r' \in [N^{1/4}]\}}$ of length ${\lfloor N^{1/4}\rfloor}$ and spacing ${d^2}$ on which ${A}$ has density at least ${\delta + c\delta^3}$ (and hence at least ${\delta_0+c\delta_0^3}$ ) for some absolute constant ${c>0}$ . If we then apply the induction hypothesis to the set

$\displaystyle A' := \{ r' \in [N^{1/4}]: n' + d^2 r' \in A \}$

we conclude (for ${N}$ large enough) that ${A'}$ contains a pair ${m, m+s^2}$ for some natural numbers ${m,s}$ with ${s}$ non-zero. This implies that ${(n'+d^2 m), (n'+d^2 m) + (|d|s)^2}$ lie in ${A}$ , a contradiction, establishing the implication (1).

A more careful analysis of the above argument reveals a more quantitative version of Theorem 1: for ${N \geq 100}$ (say), any subset of ${[N]}$ of density at least ${C/(\log\log N)^{1/2}}$ for some sufficiently large absolute constant ${C}$ contains a pair ${n,n+r^2}$ with ${r}$ non-zero. This is not the best bound known; a (difficult) result of Pintz, Steiger, and Szemeredi allows the density to be as low as ${C / (\log N)^{\frac{1}{4} \log\log\log\log N}}$ . On the other hand, this already improves on the (simpler) Fourier-analytic argument of Green that works for densities at least ${C/(\log\log N)^{1/11}}$ (although the original argument of Sarkozy, which is a little more intricate, works up to ${C (\log\log N)^{2/3}/(\log N)^{1/3}}$ ). In the other direction, a construction of Rusza gives a set of density ${\frac{1}{65} N^{-0.267}}$ without any pairs ${n,n+r^2}$ .

Remark 1 A similar argument also applies with ${n,n+r^2}$ replaced by ${n,n+r^k}$ for fixed ${k}$ , because this sort of pattern is preserved by affine dilations ${r' \mapsto n'+d^k r'}$ into arithmetic progressions whose spacing ${d^k}$ is a ${k^{th}}$ power. By re-introducing Fourier analysis, one can also perform an argument of this type for ${n,n+d,n+2d}$ where ${d}$ is the sum of two squares; see the above-mentioned paper of Green for details. However there seems to be some technical difficulty in extending it to patterns of the form ${n,n+P(r)}$ for polynomials ${P}$ that consist of more than a single monomial (and with the normalisation ${P(0)=0}$ , to avoid local obstructions), because one no longer has this preservation property.

26 comments

Comments feed for this article

28 February, 2013 at 11:16 pm

Hossein

WOW!

1 March, 2013 at 1:30 am

anon

Typo: “Suppose for sake of contradiction that …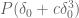 $P(\delta_0 + c\delta_0^3)$ holds” – should this be $P(\delta_0 + c\delta_0^4)$ ?

[Corrected, thanks. Actually I found just now that one could actually get back the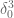 $\delta_0^3$ gain in density by being a bit more careful with the Cauchy-Schwarz, and updated the post accordingly. -T]

1 March, 2013 at 4:09 am

Michael

In the three equations before equation (2) I think r+h+h’ should be 2r+h+h’

[Corrected, thanks – T.]

1 March, 2013 at 6:32 am

Anonymous

Thank you for the nice post! Actually, through shifting by (r+h)^2 one obtains 2r instead of r, and later 2rd but this is a minor thing.

1 March, 2013 at 6:38 am

Gil Kalai

Terry, What are the upper and lower bounds on the required density in this case?

[Thanks for the question! I just added a link to the best known lower bound, by Ruzsa, at the end of this post. The best known upper bound is due to Pintz, Steiger, and Szemeredi and is also given at the end of the post. -T.]

2 March, 2013 at 3:03 am

Ben Green

Terry, I don’t think my arguments from 2002 give 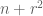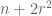$n$ , $n + r^2$ , $n + 2r^2$ – in the paper you refer to, the common difference has to be a sum of two squares, a much weaker result. Also, the original Fourier -analytic argument of S\’ark\”ozy, which is not too complicated, gives a bound of $(\log N)^{-c}$ . The idea of this argument is to make sure your large Fourier coefficient is near a low-complexity rational, so you pass to a subprogression with small common difference.

[Corrected, thanks – T.]

2 March, 2013 at 10:45 am

Gil Kalai

Thanks for the lower bound, Terry, That’s quite a gap :)

I have another question: For Roth we have 2 finite alphabet analogs: The first is DHJ(3) (the density Hales Jewett for 3-letters alphabet) and the second is the cupset problem (a set of (0,1,n}^n without an affine line). (Of course, there are intermediate problems, etc.)

For Furstenberg-Sarkozy we have a DHJ analog (which is the first case of a polynomial DHJ that Tim proposed to study; it is over a 2-letters alphabet, the ground set has the structure of edges of a complete graph, and asks for a Sperner theorem where the difference correspond to a complete graph).

The first unknown case of polynomial DHJ

My question is about an analog analogous to the the cupset analog. Maybe you have to exclude a difference is in a quadric? Do you know?

(If the forbidden things will includes those of the polynomial DHJ this would be nice but not necessary)

2 March, 2013 at 11:48 am

Terence Tao

Well, the most direct capset analogue of the Furstenberg-Sarkozy theorem is that every dense subset of the polynomial ring ${\bf F}_3[t]$ contains a pair of polynomials of the form $p(t), p(t)+q(t)^2$ for $q(t)$ non-zero. 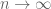Here density is in the sense that the density in the space of polynomials of degree less than $n$ (which is isomorphic as a vector space to ${\bf F}_3^n$ ) is bounded from below as $n \to \infty$ . Pretty much any of the known proofs of the Furstenberg-Sarkozy theorem will adapt to this finite field setting (and in fact the arguments will usually become a little bit simpler) But this is not a purely alphabetical statement, because the operation of squaring a polynomial becomes quite complicated if one attempts to interpret it purely in terms of combinatorial operations on the coefficients (it is convolution rather than pointwise addition).

2 March, 2013 at 11:58 am

Gil Kalai

That’s fine, but why F_3 and not F_2?

2 March, 2013 at 4:18 pm

Terence Tao

The squaring function $q(t) \mapsto q(t)^2$ behaves quite differently in characteristic 2 as compared to odd (or zero) characteristic; in particular, in this characteristic the squaring function becomes linear ( $q(t)^2 = q(t^2)$ ), and the result here collapses to something more analogous to the Ajtai-Szemeredi corners theorem than the Furstenberg-Sarkozy theorem.

14 March, 2013 at 1:19 pm

Gil Kalai

Regarding $Z_p^n$ as representing polynomials in one variable of degree less than n is very natural, but we can have other versions, e.g., polynomials of degree 2 in some m variables (or “bipartite” polynomials of degree 2) , which may make sense over $Z_2$ as well. In particular, it will be nice to have cupset versions related to versions of polynomial HJT that Tim Gowers considered here http://gowers.wordpress.com/2009/11/14/the-first-unknown-case-of-polynomial-dhj/ .

3 March, 2013 at 1:33 pm

Neil Lyall

Terry, thanks for the very nice post!

Just wanted to point out that I believe the argument you present can be adapted in a standard way, using Lucier’s increment strategy (with the polynomials changing with each iteration), to obtain the analogous result for full class of so-called intersective polynomials. A nice exposition of Lucier’s iterative procedure can be found at the beginning of Chapter 6 (pp 40-42) of Alex Rice’s Ph.D. thesis, see http://www.math.uga.edu/~arice/AlexThesis.pdf

A quick calculation seems to give a bound of the order
$C_k/(\log\log N)^{1/2^{k-1}}$ for intersective polynomials of degree $k$ .

10 March, 2013 at 6:45 am

Joseph

Thank you for one more great post. You work inspire me, Dr. Tao.

Can anyone help me with a very basic question? How does (1) guarantee that the infimus of the set of all \delta>0 for which P(\delta) holds is zero? And how does analyzing this leads to the fact that P holds for all \delta>0?

Sorry for the basic question, but I got stuck.

10 March, 2013 at 10:22 am

anon

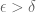Define the set $A = \{\delta: P(\delta)\}$ . If $\delta \in A$ then for any $\epsilon > \delta$ we have $\epsilon \in A$ , simply because the theorem is stronger for smaller $\delta$ . So the set is some interval (closed $[\delta_0, \infty)$ or open $(\delta_0,\infty)$ ) and trivially it contains 1. Let’s call $\delta_0$ infimum of $A$ . $\delta_0$ may or may not be in $A$ but anything greater than it definitely is in $A$ .

If $\delta_0 = 0$ , then we are done, since this means $A$ contains any positive value, which proves the theorem. So let’s assume $\delta_0 > 0$ and derive a contradiction.

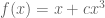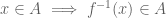Let $f(x) = x + c x^3$ . Note that $f$ is (strictly) increasing and continuous. From (1) we have $f(x) \in A \implies x \in A$ . Equivalently, $x \in A \implies f^{-1}(x) \in A$ .

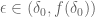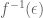Take any number $\epsilon \in (\delta_0, f(\delta_0))$ . Since $\epsilon > \delta_0$ we have $\epsilon \in A$ , therefore $f^{-1}(\epsilon) \in A$ . But since $\epsilon < f(\delta_0)$ we have $f^{-1}(\epsilon) < \delta_0$ . So we have a number $f^{-1}(\epsilon)$ which is in $A$ and smaller than $\delta_0$ , contradiction.

10 March, 2013 at 12:14 pm

Joseph

Dear anon,

Thank you for your nice explanation!

I now got the idea.

Sincerely, Joseph

11 March, 2013 at 6:20 am

Joseph

Dear anon,

Thank you again. But just a quick question: as we define f(x) = x+cx^3, can we consider the same value of c for all x? I mean, the beginning of Tao’s proof says that for any 0<delta00. Can we then fix c when defining f(x) (for example, by taking a c that satisfies (1) for any delta, if such one exists)?

Otherwise, if we state f(x) = x+c(x)x^3, with c now a function, can we still guarantee that f is invertible?

Sorry if the question is too basic… This is a new field for me.

Regards,

Joseph.

[It appears that you used some < and > signs in your answer that became interpreted as HTML and thus disappeared. If you use < and > instead then this should avoid the problem. In any case, $c$ is indeed the fixed absolute constant from (1). -T.]

13 March, 2013 at 6:45 pm

Joseph

Never mind, I got it… Once you assume that the infimum is delta0 > 0, you define f(x) = x+cx^3, with c the value that satisfies (1) for that particular delta0 value (so, yes, a unique value for c). Than f is of course increasing and continuous, and everything else follows… I was thinking in a different way, but your explanation was perfect. Thanks!

23 March, 2013 at 7:50 am

solver6

Hello, i don’t understand wy ${\bf E}_{n\in [N]}{\bf E}_{r\in [N^{1/3}]}{\bf E}_{h\in[n^{1/100}]}1_A(n)\delta1_{[N]}(n+(r+h)^2)={\delta}^2+O(N^{1/3})$ holds. Can someone help me.

23 March, 2013 at 9:21 am

Terence Tao

For all but about $O(N^{2/3})$ of the choices of n (the choices that are closest to the boundary of $[N]$ , the inner average ${\bf E}_{r \in [N^{1/3}]} {\bf E}_{h \in [n^{1/100}]} \delta 1_{[N]}(n+(r+h)^2)$ is equal to $\delta$ .

19 April, 2013 at 6:32 am

Anonymous

Hi, I don’t understand the move from the inequality depending only on $h,n,r$ to the one depending also on $h’$.

Any help?

19 April, 2013 at 8:21 am

Terence Tao

$|{\bf E}_{h \in A} c(h)|^2 = {\bf E}_{h \in A} {\bf E}_{h' \in A} c(h) c(h')$ whenever $c(h)$ is real-valued.

21 April, 2013 at 9:33 am

Anonymous

Maybe the left side should be squared?

[Corrected, thanks – T.],

6 May, 2015 at 8:39 am

Ned

Hi, I need some help: I don’t understand how Cauchy-Schwarz is applied.

6 May, 2015 at 2:26 pm

Terence Tao

Cauchy-Schwarz bounds ${\bf E}_{n \in [N]} {\bf E}_{r \in [N^{1/3}]} |f(n)| | E_{h \in [N^{1/100}]} f(n+(r+h)^2)|$ by the geometric mean of ${\bf E}_{n \in [N]} |f(n)|^2$ and ${\bf E}_{n \in [N]} {\bf E}_{r \in [N^{1/3}]} | E_{h \in [N^{1/100}]} f(n+(r+h)^2)|^2$ .

8 May, 2015 at 12:26 am

Ned

thanks!

25 December, 2023 at 7:31 pm

Marcel Goh

Let $P$ be the progression $\{n + dr : r\in [N^{1/3}]$ obtained near the end of the proof. I think strictly speaking, the fact that ${\bf E}_{r\in [N^{1/3}]} f(n+dr) \gg \delta^3$ only gives us $|A\cap P| / |P| \ge c\delta^3 + \delta |[N]\cap P|\over |P|$ . But to ensure that $P\subseteq [N]$ , we can throw away the largest $2N^{1/3+1/100}$ elements of $[N]$ at the cost of introducing an error term of $O(N^{-2/3+1/100})$ . (This doesn’t matter because the whole thing will still be $\gg \delta^3$ .) Then we only sum over $n\in [N-2N^{1/3+1/100}]$ , and the elements $n+dr$ will always be in $[N]$ .

	Anonymous on Erratum for “An inverse…
	Anonymous on Infinite partial sumsets in th…
	Anonymous on Infinite partial sumsets in th…
	Anonymous on A Banach algebra proof of the…
	Anonymous on A Banach algebra proof of the…
	Aleksandar on 245C, Notes 4: Sobolev sp…
	Anonymous on Erratum for “An inverse…
	Anonymous on Erratum for “An inverse…
	Anonymous on Erratum for “An inverse…
	Anonymous on Erratum for “An inverse…
	Terence Tao on 245C, Notes 4: Sobolev sp…
	Terence Tao on 275A, Notes 3: The weak and st…
	Terence Tao on What is a gauge?
	Terence Tao on Erratum for “An inverse…
	Terence Tao on 275A, Notes 3: The weak and st…

A Fourier-free proof of the Furstenberg-Sarkozy theorem

Recent Comments

Articles by others

Diversions

Mathematics

Selected articles

Software

The sciences

Top Posts

Archives

Categories

The Polymath Blog

26 comments

Leave a comment Cancel reply

For commenters

A Fourier-free proof of the Furstenberg-Sarkozy theorem

Share this:

Recent Comments

Articles by others

Diversions

Mathematics

Selected articles

Software

The sciences

Top Posts

Archives

Categories

The Polymath Blog

26 comments

Leave a comment Cancel reply

For commenters