The lonely runner conjecture is the following open problem:
Conjecture 1 Suppose one has
runners on the unit circle
, all starting at the origin and moving at different speeds. Then for each runner, there is at least one time
for which that runner is “lonely” in the sense that it is separated by a distance at least
from all other runners.
One can normalise the speed of the lonely runner to be zero, at which point the conjecture can be reformulated (after replacing by
) as follows:
Conjecture 2 Let
be non-zero real numbers for some
. Then there exists a real number
such that the numbers
are all a distance at least
from the integers, thus
where
denotes the distance of
to the nearest integer.
This conjecture has been proven for , but remains open for larger
. The bound
is optimal, as can be seen by looking at the case
and applying the Dirichlet approximation theorem. Note that for each non-zero
, the set
has (Banach) density
for any
, and from this and the union bound we can easily find
for which
for any , but it has proven to be quite challenging to remove the factor of
to increase
to
. (As far as I know, even improving
to
for some absolute constant
and sufficiently large
remains open.)
The speeds in the above conjecture are arbitrary non-zero reals, but it has been known for some time that one can reduce without loss of generality to the case when the
are rationals, or equivalently (by scaling) to the case where they are integers; see e.g. Section 4 of this paper of Bohman, Holzman, and Kleitman.
In this post I would like to remark on a slight refinement of this reduction, in which the speeds are integers of bounded size, where the bound depends on
. More precisely:
Proposition 3 In order to prove the lonely runner conjecture, it suffices to do so under the additional assumption that the
are integers of size at most
, where
is an (explicitly computable) absolute constant. (More precisely: if this restricted version of the lonely runner conjecture is true for all
, then the original version of the conjecture is also true for all
.)
In principle, this proposition allows one to verify the lonely runner conjecture for a given in finite time; however the number of cases to check with this proposition grows faster than exponentially in
, and so this is unfortunately not a feasible approach to verifying the lonely runner conjecture for more values of
than currently known.
One of the key tools needed to prove this proposition is the following additive combinatorics result. Recall that a generalised arithmetic progression (or ) in the reals
is a set of the form
for some and
; the quantity
is called the rank of the progression. If
, the progression
is said to be
-proper if the sums
with
for
are all distinct. We have
Lemma 4 (Progressions lie inside proper progressions) Let
be a GAP of rank
in the reals, and let
. Then
is contained in a
-proper GAP
of rank at most
, with
Proof: See Theorem 2.1 of this paper of Bilu. (Very similar results can also be found in Theorem 3.40 of my book with Van Vu, or Theorem 1.10 of this paper of mine with Van Vu.)
Now let , and assume inductively that the lonely runner conjecture has been proven for all smaller values of
, as well as for the current value of
in the case that
are integers of size at most
for some sufficiently large
. We will show that the lonely runner conjecture holds in general for this choice of
.
let be non-zero real numbers. Let
be a large absolute constant to be chosen later. From the above lemma applied to the GAP
, one can find a
-proper GAP
of rank at most
containing
such that
in particular if
is large enough depending on
.
We write
for some ,
, and
. We thus have
for
, where
is the linear map
and
are non-zero and lie in the box
.
We now need an elementary lemma that allows us to create a “collision” between two of the via a linear projection, without making any of the
collide with the origin:
Lemma 5 Let
be non-zero vectors that are not all collinear with the origin. Then, after replacing one or more of the
with their negatives
if necessary, there exists a pair
such that
, and such that none of the
is a scalar multiple of
.
Proof: We may assume that , since the
case is vacuous. Applying a generic linear projection to
(which does not affect collinearity, or the property that a given
is a scalar multiple of
), we may then reduce to the case
.
By a rotation and relabeling, we may assume that lies on the negative
-axis; by flipping signs as necessary we may then assume that all of the
lie in the closed right half-plane. As the
are not all collinear with the origin, one of the
lies off of the
-axis, by relabeling, we may assume that
lies off of the
axis and makes a minimal angle with the
-axis. Then the angle of
with the
-axis is non-zero but smaller than any non-zero angle that any of the
make with this axis, and so none of the
are a scalar multiple of
, and the claim follows.
We now return to the proof of the proposition. If the are all collinear with the origin, then
lie in a one-dimensional arithmetic progression
, and then by rescaling we may take the
to be integers of magnitude at most
, at which point we are done by hypothesis. Thus, we may assume that the
are not all collinear with the origin, and so by the above lemma and relabeling we may assume that
is non-zero, and that none of the
are scalar multiples of
.
with for
; by relabeling we may assume without loss of generality that
is non-zero, and furthermore that
where is a natural number and
have no common factor.
We now define a variant of
by the map
where the are real numbers that are linearly independent over
, whose precise value will not be of importance in our argument. This is a linear map with the property that
, so that
consists of at most
distinct real numbers, which are non-zero since none of the
are scalar multiples of
, and the
are linearly independent over
. As we are assuming inductively that the lonely runner conjecture holds for
, we conclude (after deleting duplicates) that there exists at least one real number
such that
We would like to “approximate” by
to then conclude that there is at least one real number
such that
It turns out that we can do this by a Fourier-analytic argument taking advantage of the -proper nature of
. Firstly, we see from the Dirichlet approximation theorem that one has
for a set of reals of (Banach) density
. Thus, by the triangle inequality, we have
for a set of reals of density
.
Applying a smooth Fourier multiplier of Littlewood-Paley type, one can find a trigonometric polynomial
which takes values in , is
for
, and is no larger than
for
. We then have
where denotes the mean value of a quasiperiodic function
on the reals
. We expand the left-hand side out as
From the genericity of , we see that the constraint
occurs if and only if is a scalar multiple of
, or equivalently (by (1), (2)) an integer multiple of
. Thus
and is the Dirichlet series
By Fourier expansion and writing , we may write (4) as
The support of the implies that
. Because of the
-properness of
, we see (for
large enough) that the equation
and conversely that (7) implies that (6) holds for some with
. From (3) we thus have
In particular, there exists a such that
Since is bounded in magnitude by
, and
is bounded by
, we thus have
for each , which by the size properties of
implies that
for all
, giving the lonely runner conjecture for
.

58 comments
Comments feed for this article
13 May, 2015 at 10:27 pm
domotorp
I’m in a hurry, but we have also investigated results similar to Lemma 4: http://arxiv.org/abs/0912.0424. One can show that a single exponential bound in d is not sufficient using this result of Alon and Vu: http://www.math.tau.ac.il/~nogaa/PDFS/av1.pdf.
14 May, 2015 at 8:54 pm
domotorp
I’m sorry, now after taking a proper look, our results seem unrelated, they just contain similar words and bounds.
14 May, 2015 at 1:24 am
Anonymous
In conjecture 2, it seems that “the origin” should be “the integers”.
[Corrected, thanks – T.]
14 May, 2015 at 4:42 am
Bogdan
You proved that if the conjecture is false for a given n, then it false for SOME v_1, …, v_n of size n^(Cn^2). Can similar methods to be extended to prove a stronger result, that if the conjecture is false for a given n, then it false for MANY v_1, …, v_n of size n^(Cn^2), say, for a positive proportion (independent of n) of all tuples v_1, …, v_n of this size. Then, for the first unproved case n=8, we could check the conjecture for some RANDOM tuples bouded by 8^64C (if C is not too lagre), and, if true, confirm the original conjecture for n=8, with probability, arbitrary closed to 1.
14 May, 2015 at 10:28 am
Terence Tao
One can certainly establish the conjecture for “most” choices of ; for instance, if the
; for instance, if the  are linearly independent over
are linearly independent over 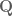 (which occurs for almost every choice of reals
(which occurs for almost every choice of reals  ), then the
), then the  behave as independent random variables and the claim is quite easy to show in this case. However, all of the difficulty of the problem is concentrated in “special” choices of
behave as independent random variables and the claim is quite easy to show in this case. However, all of the difficulty of the problem is concentrated in “special” choices of  , and knowing that the conjecture is true for “most” choices doesn’t make much impact on this most difficult case. (An analogy is with Fermat’s last theorem: it is easy to show that the equation
, and knowing that the conjecture is true for “most” choices doesn’t make much impact on this most difficult case. (An analogy is with Fermat’s last theorem: it is easy to show that the equation 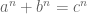 is false for “most” choices of $a,b,c,n$, for just about any notion of “most”, but this does not really make a dent in solving the problem.)
is false for “most” choices of $a,b,c,n$, for just about any notion of “most”, but this does not really make a dent in solving the problem.)
15 May, 2015 at 2:22 am
Bogdan
You completely misundersood my comment :) I wil try again.
Your theorem is: If there is at least one counterexample for ANY v_1, …, v_n, then there is at least ONE counterexample for bounded v_1, …, v_n.
Now, assume we have a stronger result, namely:
Statement A: If there is at least one counterexample for any v_1, …, v_n, then positive proportion of ALL bounded v_1, …, v_n are all counterexamples.
Then, trying at random, we could rule out a possibility that positive proportion of ALL bounded v_1, …, v_n are all counterexamples, and
use statement A to prove the result in full.
Example how this may work.
Statement B: If there is at least one counterexample N to odd Goldbach’s conjecture, then at least N/log N even numbers in the region from 2 to N are ALL counterexamples to even Goldbach’s conjecture.
Proof is trivial. If N is a counterexample to odd Goldbach’s conjecture, then N-p is a counterexample to the even Goldbach’s conjecture for any odd p less than N.
Now, we can check even Goldbach’s conjecture for sufficiently many random numbers below exp(3100), and the odd Goldbach’s conjecture for numbers below exp(3100) follows from statement B. See https://rjlipton.wordpress.com/2014/06/06/is-this-a-proof-2/ for a variant of this argument.
15 May, 2015 at 7:25 am
Terence Tao
Ah, I see what you are saying now. I doubt that this sort of “counterexample dispersion” effect is present in this problem; roughly speaking, the only symmetry we have available in this problem to convert one counterexample into many counterexamples are Freiman homomorphisms. (There is a technicality here in that there is some loss in the lower bound on runner separation every time one applies such a homomorphism, based on the quality of that homomorphism, but let me ignore this technicality for sake of current discussions.) There are enough homomorphisms present to “rectify” any finite set of speeds into a set of bounded integers, but not enough to obtain a positive proportion of such sets. As mentioned in my previous comment, for randomly selected sets of speeds (which all lie, more or less, in a single Freiman isomorphism class) the claim is trivial to prove, but this does not have much bearing on all the other Freiman isomorphism classes (and if the conjecture is to fail, it is likely to come from a very special, carefully constructed, Freiman isomorphism class, which will not be detectable by random search).
14 May, 2015 at 6:39 am
Anonymous
It seems that the (closely related) Littlewood conjecture complements this conjecture for (where
(where  is constrained to be an integer.)
is constrained to be an integer.)
15 May, 2015 at 12:21 am
Anonymous
Correction: In conjecture 1 (to be exactly equivalent to conjecture 2), it seems that “different speeds” should be interpreted as “there is at least one runner whose speed is different from the speeds of the other runners”.
[The formulations are equivalent, as can be seen by replacing multiple runners with the same speed with a single runner of that speed. -T.]
15 May, 2015 at 8:05 am
Anonymous
The simple identity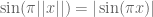 implies that conjecture 2 has the following analytic formulation
implies that conjecture 2 has the following analytic formulation
It is easy to verify that the (outer) maximum is attained at an intersection point of two sine curves (with corresponding velocities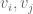 ), i.e.
), i.e.
Implying that is rational (a multiple of
is rational (a multiple of  or
or 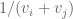 ).
).
Therefore (without loss of generality) may be assumed to be rational (with denominator being the sum or difference of two integer velocities).
may be assumed to be rational (with denominator being the sum or difference of two integer velocities).
15 May, 2015 at 3:01 pm
arch1
Is Conjecture 2 equivalent to asking whether one can see infinitely far from the origin in an n-space occupied by opaque n-cubes of side length (n-1)/(n+1) centered at half-integer coordinates?
..and no fair peeking down a coordinate axis:-)
17 May, 2015 at 12:15 am
Terence Tao
Yes; indeed, the original literature on the lonely runner conjecture was motivated by such “view-obstruction” formulations of the problem.
17 May, 2015 at 9:06 am
arch1
Thanks. As a layperson this motivates me to try understand more of this posting. At first blush, it’s very surprising to me that such a basic view obstruction question, in such an apparently simple, symmetrical, static setting, is so hard.
16 May, 2015 at 9:18 am
Drive by shooting
Would you buy this argument?
We can generalize the velocities to be arbitrary real numbers, for example by choosing a frame of reference traveling with an arbitrary runner. The system then satisfies the constraints of the Poincare recurrence theorem, for the
velocities to be arbitrary real numbers, for example by choosing a frame of reference traveling with an arbitrary runner. The system then satisfies the constraints of the Poincare recurrence theorem, for the  positions, and the
positions, and the  velocities. But any group of $n-1$ runners must then also fulfill the constraints of the Poincare recurrence theorem. Thus, fix a reference frame to an arbitrary runner, and consider a volume of the position space of the remaining
velocities. But any group of $n-1$ runners must then also fulfill the constraints of the Poincare recurrence theorem. Thus, fix a reference frame to an arbitrary runner, and consider a volume of the position space of the remaining 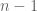 runners, of length
runners, of length 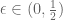 for each of the
for each of the 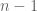 runners, and exactly opposite to the origin of the chosen runner. By the Poincare recurrence theorem the
runners, and exactly opposite to the origin of the chosen runner. By the Poincare recurrence theorem the 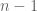 runners must revisit this volume infinitely often. We then have for any
runners must revisit this volume infinitely often. We then have for any 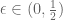 each runner is separated from all the other runners by that amount infinitely often.
each runner is separated from all the other runners by that amount infinitely often.
17 May, 2015 at 12:15 am
Terence Tao
In order to apply the Poincare recurrence theorem, the region of space considered must be visited at least once before one can conclude that it is visited infinitely often. (With stronger hypotheses on the dynamical system, such as minimality, one does not need this additional hypothesis, however the system will only be minimal in the easy case when the relative velocities are linearly independent over the rationals.)
17 May, 2015 at 1:42 am
James Smith
A small thing that confused me: you say in your definition of the problem that all the runners start at the origin. To say they start at the same place might be a little clearer. And I wonder now I come to think of it if the circle were indeed replaced with a disc how the problem would unfold.
[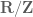 denotes the additive unit circle, rather than the multiplicative (or geometric) unit circle
denotes the additive unit circle, rather than the multiplicative (or geometric) unit circle 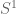 – one can think of it as the geometric unit circle transformed by a logarithmic change of variables. In particular, the identity element 1 of the multiplicative unit circle becomes the identity element 0 of the additive unit circle. -T.]
– one can think of it as the geometric unit circle transformed by a logarithmic change of variables. In particular, the identity element 1 of the multiplicative unit circle becomes the identity element 0 of the additive unit circle. -T.]
17 May, 2015 at 1:18 pm
James Smith
I never made the distinction before. Thanks for clearing it up!
17 May, 2015 at 7:33 pm
victor
What if the velocities are random, ie, the velocity of the $i$th runner is $v_0 \exp( \mu t + \sigma B^i_t)$ where $B^i_t$ is standard Brownian Motion and is independent across the runners? The deterministic problem is the limiting case where $\mu = 0$ and $\sigma= \infty$. Would it make sense to solve the stochastic problem first?
18 May, 2015 at 9:14 am
Terence Tao
This is an irreducible Markov process (where the state space tracks both position and velocity) and so the stochastic runners will almost surely traverse a dense set of states, which amongst other things establishes the lonely runner property for such a set of runners. The difficulty in this conjecture lies not with such “generic” situations, but rather with very special “arithmetically structured” situations in which the runner velocities all have a rigid relationship with each other (e.g. they are all rational multiples of each other with small height).
18 May, 2015 at 9:22 am
victor
Thanks for clarifying Prof Tao.
27 October, 2015 at 6:23 am
Antoine
Hello, with all my respect, Dr. Tao, your point of the optimal and relation to the Dirichlet approximation theorem. well i haven’t seen that, from the stated theorem at wiki,
and relation to the Dirichlet approximation theorem. well i haven’t seen that, from the stated theorem at wiki,  is what precisely in the theorem? thanks.
is what precisely in the theorem? thanks.
[The would correspond to the “
would correspond to the “ ” in the Wikipedia formulation of the theorem (and the time
” in the Wikipedia formulation of the theorem (and the time  would correspond to
would correspond to  , and
, and  to
to  ). -T]</I<
). -T]</I<
20 November, 2015 at 3:37 am
Antoine
Thanks sorry i didn’t expect a reply!, anyway the $q$ depends on $\alpha $ in the theorem no, so for a fixed $q$ maybe there exist $\alpha$ such that the less or equal is bigger or equal, did i miss something? t.y.
20 November, 2015 at 3:39 am
Antoine
No Tex sorry.
20 November, 2015 at 8:36 am
Terence Tao
The Dirichlet approximation theorem (with the substitutions indicated) tells us that for any real , there exists a
, there exists a  between
between  and
and  (depending on
(depending on  ) such that
) such that 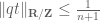 . Setting
. Setting  for
for 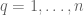 , we conclude that Conjecture 2 fails if the quantity
, we conclude that Conjecture 2 fails if the quantity 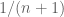 is replaced by any smaller quantity.
is replaced by any smaller quantity.
20 November, 2015 at 8:47 am
Anonymous
Thank you.
19 December, 2015 at 8:20 am
Antoine
Thanks
12 January, 2016 at 12:08 pm
Elliott
Prof. Tao, can’t the bound 1/(n+1) be seen to be optimal without referring to the Dirichlet approximation theorem? For speeds 1,…,n let t = 1/(n+1). Then ||1/(n+1)|| and ||n/(n+1)|| both equal 1/(n+1).
12 January, 2016 at 4:16 pm
Terence Tao
This doesn’t immediately preclude Conjecture 2 holding with 1/(n+1) replaced by a larger bound, because there could be a different value of t (other than t = 1/(n+1)) in which the numbers t, 2t, …, nt are further away from the origin than in your example. (But this scenario is ruled out by the Dirichlet approximation theorem.)
25 April, 2019 at 2:52 am
Stephen Mc Guire
Dirichlet’s theorem tells us that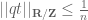 not that
not that 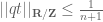 . So we can, at best, conclude that all runners are within
. So we can, at best, conclude that all runners are within  of the lonely runner i.e. the runner stationary at 0. Perhaps I’m misunderstanding something?
of the lonely runner i.e. the runner stationary at 0. Perhaps I’m misunderstanding something?
26 April, 2019 at 1:32 pm
Terence Tao
The Dirichlet approximation theorem does indeed show that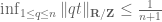 for all
for all  and all natural numbers
and all natural numbers 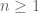 . (For some reason the Wikipedia entry only gives the weaker estimate
. (For some reason the Wikipedia entry only gives the weaker estimate  , but the stronger bound is what actually comes out of carefully optimising the proof, and in particular observing that some pair amongst
, but the stronger bound is what actually comes out of carefully optimising the proof, and in particular observing that some pair amongst  must be at a distance at most
must be at a distance at most 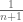 from each other.)
from each other.)
20 November, 2015 at 12:14 am
koza3301
Could you explain how to prove that “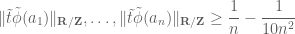 for a set
for a set 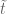 of reals of (Banach) density
of reals of (Banach) density 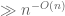 ” from the Dirichlet approximation theorem?
” from the Dirichlet approximation theorem?
20 November, 2015 at 8:35 am
Terence Tao
Cover the n-torus by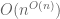 boxes of sidelength
boxes of sidelength 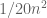 . By the Dirichlet box principle (pigeonhole principle), one of these boxes will contain
. By the Dirichlet box principle (pigeonhole principle), one of these boxes will contain 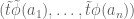 for a set of
for a set of 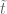 of positive density. Now subtract to get the claim. (This argument is identical to the one used to prove the usual Dirichlet approximation theorem. There are some technical issues regarding the nature of density used here, but by using some equidistribution theory one can show that all the usual notions of density (lower Banach, upper Banach, etc.) agree for the sets in question.)
of positive density. Now subtract to get the claim. (This argument is identical to the one used to prove the usual Dirichlet approximation theorem. There are some technical issues regarding the nature of density used here, but by using some equidistribution theory one can show that all the usual notions of density (lower Banach, upper Banach, etc.) agree for the sets in question.)
20 November, 2015 at 8:43 am
koza3301
Thanks :)
19 December, 2015 at 8:32 am
Antoine
Hi, I’ve got another question Prof. Tao if no bother; a result such as: their exist infinite times when say the $k$ runners are all distant from each other by at least $a\dfrac{1}{k}$ with $a$ less than $1,$ can be bigger than $\dfrac{1}{2}$ and it depends on the speed of the $k$ runners, Where it stands on a crowded scale for this problem, thanks all respect.
23 March, 2016 at 9:53 pm
David R
What do you think of this argument Prof. Tao? Suppose we use the following three lemmas to prove the slowest runner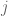 becomes lonely:
becomes lonely:
Lemma 1: Let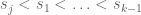 for
for 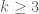 . Then
. Then 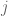 becomes lonely if and only if there exists
becomes lonely if and only if there exists 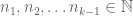 such that
such that ![\bigcap_{i = 1}^{k - 1} \bigg [\frac{n_i + \frac{1}{k}}{s_i - s_j}, \frac{n_i + \frac{k - 1}{k}}{s_i - s_j}\bigg ] \neq \emptyset](https://s0.wp.com/latex.php?latex=%5Cbigcap_%7Bi+%3D+1%7D%5E%7Bk+-+1%7D+%5Cbigg+%5B%5Cfrac%7Bn_i+%2B+%5Cfrac%7B1%7D%7Bk%7D%7D%7Bs_i+-+s_j%7D%2C++%5Cfrac%7Bn_i+%2B+%5Cfrac%7Bk+-+1%7D%7Bk%7D%7D%7Bs_i+-+s_j%7D%5Cbigg+%5D+%5Cneq+%5Cemptyset&bg=ffffff&fg=545454&s=0&c=20201002)
Proof:: Straightforward in both directions.
Lemma 2: Let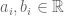 and
and 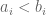 . Then
. Then ![\bigcap_{i = 1}^{k} [a_i, b_i] \neq \emptyset](https://s0.wp.com/latex.php?latex=%5Cbigcap_%7Bi+%3D+1%7D%5E%7Bk%7D+%5Ba_i%2C+b_i%5D+%5Cneq+%5Cemptyset&bg=ffffff&fg=545454&s=0&c=20201002) if and only if
if and only if  for all
for all 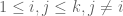 ..
..
Proof: ( ). Proof by contradiction.
). Proof by contradiction. ). Proof by contrapositive.
). Proof by contrapositive.
(
Lemma 3: Let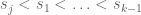 for
for 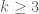 .Then there exists
.Then there exists 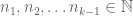 such that
such that
for ,
, 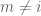 .
.
Proof: Try a proof by induction. Proving the base case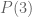 follows easily from the fact that the LRC has been proven for
follows easily from the fact that the LRC has been proven for 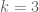 . Proving that
. Proving that  looks to be quite difficult though.
looks to be quite difficult though.
We can then make the following argument:
Theorem 1: Let . Then
. Then  becomes lonely.
becomes lonely.
Proof: By Lemma 3, there exists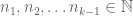 such that
such that
for all ,
, 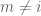 . Hence, there exists
. Hence, there exists 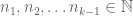 such that
such that
for all ,
, 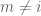 . By setting
. By setting
and because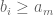 for
for 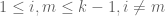 we have from Lemma 2,
we have from Lemma 2,
By Lemma 1, becomes lonely for all T in the intersection.
becomes lonely for all T in the intersection.
The thing that’s interesting about this argument is that if we can prove Lemma 3, then we can repeat essentially the same argument to prove that runners with some intermediate speed as well as runners with the fastest speed become lonely. The argument for proving that the fastest runner becomes lonely would be almost identical to the argument for the slowest runner.
7 June, 2016 at 5:48 am
Klaus85
Dear Terry, I have just found this arxiv-paper (http://arxiv.org/abs/1606.01783) claiming to proof the lonely-runner conjecture. It is the highest-rated paper of today on scirate, thus i thought it might be serios; but i would love to hear more details by an expert. Does it investigate the same question as mentioned here, or is it a weaker variation? Thanks so much!
7 June, 2016 at 4:33 pm
Terence Tao
The paper has been withdrawn due to an error on the last line.
7 June, 2016 at 4:58 pm
anthonyquas
Can you say in more detail where the error was?
7 June, 2016 at 5:38 pm
Terence Tao
The final inequality is not true in the case.
case.
7 June, 2016 at 8:50 pm
David Lui
do you think this is an easily fixable problem, or would it require significant effort to fix, or is the proof outright wrong?
8 June, 2016 at 8:22 am
Terence Tao
Probably the author is the best person to answer this. But one test can come from the observation that the lonely runner conjecture is only barely true in the case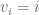 (as pointed out in above in the blog post) or permutations or affine transformations thereof. As such, any proof of the lonely runner conjecture should also only barely work in this case (in particular, any key inequality in the proof should hold with equality in this case). This did not seem to be the case in this most recent attempt to prove the conjecture, which suggests at minimum that a significant modification of the argument would be required.
(as pointed out in above in the blog post) or permutations or affine transformations thereof. As such, any proof of the lonely runner conjecture should also only barely work in this case (in particular, any key inequality in the proof should hold with equality in this case). This did not seem to be the case in this most recent attempt to prove the conjecture, which suggests at minimum that a significant modification of the argument would be required.
7 June, 2016 at 4:31 pm
anthonyquas
I have read through the Beck paper once without finding any problems in it. It does indeed address the full Lonely Runner Conjecture as described in this blog post. I am about to re-read.
7 June, 2016 at 8:41 pm
Curious Party
What time was the mistake found? A wager was placed on this result being false.
7 June, 2016 at 11:07 pm
Mike Miller
I find this to be in extremely poor taste.
8 June, 2016 at 7:42 am
David Lui
is it asking when it was found, or the wager part that you find to be in poor taste?
8 June, 2016 at 2:38 pm
Classy Mofo
Perhaps it is your own taste that is poor?
29 August, 2016 at 2:52 am
giorgi
Hello terence tao. (1,2…m-1 and i are indexes ) i just proof what conjecture is equivalent to this conjecture (i mean if we proof “”this” then lonely runner conjecture is true too): q1, q2, …qm-1 is any positive numbers , if q1, q2, …qm-1
we can Multiplicate some number k (k>0) and get this type of similar proportion numbers: C1+N1, C2+N2 , …. Cm-1+Nm-1 , were Ci are numbers between 1/m<=Ci<=(m-1)/m and Ni are natural numbers then "lonely runner" is true too. what you think about it?
p.s. im just lover of mathematics and sorry for my english and "latex"
7 September, 2016 at 8:44 am
একেলা দৌড়বিদের কনজেকচার (The Lonely Runner Conjecture) - বিজ্ঞান স্কুল
[…] আরও পড়ার জন্য দেখতে পারেন এখানে https://terrytao.wordpress.com/2015/05/13/a-remark-on-the-lonely-runner-conjecture/ […]
10 January, 2017 at 1:40 pm
Some remarks on the lonely runner conjecture | What's new
[…] to Contributions to discrete mathematics. I had blogged about the lonely runner conjecture in this previous blog post, and I returned to the problem recently to see if I could obtain anything further. The results […]
22 October, 2018 at 11:30 am
dsp
This will probably turn out to be a very stupid question, but anyway: I have been thinking about what happens when you replace the Euclidean distance in the lonely runner conjecture with the p-adic one, i. e., what can one say about the set of vectors of distances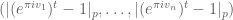 , where
, where  are fixed rational numbers,
are fixed rational numbers,  ranges over
ranges over 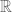 and
and  denotes the p-adic absolute value of
denotes the p-adic absolute value of  ? I’ve come up with something I can’t understand. I guess my (as I said, probably stupid) question boils down to this:
? I’ve come up with something I can’t understand. I guess my (as I said, probably stupid) question boils down to this:
1) For an algebraic number , the product of all the p-adic absolute values of
, the product of all the p-adic absolute values of  equals
equals 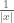 .
.
2) For any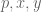 ,
, 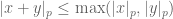
So if is a sufficiently large positive integer, since the Euclidean distance between, say, 1 and
is a sufficiently large positive integer, since the Euclidean distance between, say, 1 and 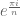 is smaller than 1, for at least one
is smaller than 1, for at least one  , we must have that the p-adic distance between the two numbers is
, we must have that the p-adic distance between the two numbers is 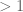 by 1). But by 2), this distance is at most
by 1). But by 2), this distance is at most  , and
, and  since it is a root of unity.
since it is a root of unity.
I hope this isn’t too far off topic.
24 October, 2018 at 9:40 am
Terence Tao
I’m not sure one can make sense p-adically of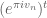 if
if  is real, since
is real, since 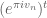 will then in general just be a transcendental complex number. However, there is some work on studying function field analogues of the lonely runner conjecture which you may be interested in: https://arxiv.org/abs/1711.01207
will then in general just be a transcendental complex number. However, there is some work on studying function field analogues of the lonely runner conjecture which you may be interested in: https://arxiv.org/abs/1711.01207
1 December, 2019 at 5:17 am
Florent L. B. Périat
Hi, Prof. Tao, I found one iterative algorithm which seems to make the times for the different runners to be lonely converge. So proving its completeness, would also proves the conjecture ? But, the program does not always converge to a solution, especially when the speeds are only integers. Would a kind of ghost decimal speed value that does not increment k help ?
PS : Sorry for my English
29 December, 2021 at 11:11 pm
Aditya Guha Roy
Prof. Tao are you aware of any literature where the authors have tried to approach this problem probabilistically.
(This problem seems to scream “use probability” in my ears, but that might be due to my lack of experience in mathematics or my obsession with probability.)
29 December, 2021 at 11:15 pm
Aditya Guha Roy
Reblogged this on Aditya Guha Roy's weblog.
7 November, 2022 at 12:42 am
martin
Has the opposite problem been considered in the literature (or elsewhere)? I would be interested whether ALL runners need to be close (how close?) to the integers at some point in time. Obviously we would need to remove the condition of start at the origin at t=0.
8 November, 2022 at 1:28 am
martin
Oh I see this is in a sense equivalent to the original problem because close to the integers means far away from the half-integers.
However for the removal of the start condition I did not find anything except a comment by Wills to a 2012 talk in Siegen by Goddyn that maybe Hans-Gill or Dumir did work on this. So the question still stands: what about removing the start condition – is there some literature?
9 November, 2022 at 1:43 am
martin
After more search, there is https://arxiv.org/abs/2009.12080 which calls the generalization the “shifted lonely runner conjecture” and proves it for 4 runners (i.e one stationary and n=3 non-stationary ones).
7 November, 2022 at 12:21 pm
Anonymous
Is it possible to show that that the conjecture is true for “almost every runners velocities” (in some sense) the conjecture is true?