Because of Euler’s identity , the complex exponential is not injective:
for any complex
and integer
. As such, the complex logarithm
is not well-defined as a single-valued function from
to
. However, after making a branch cut, one can create a branch of the logarithm which is single-valued. For instance, after removing the negative real axis
, one has the standard branch
of the logarithm, with
defined as the unique choice of the complex logarithm of
whose imaginary part has magnitude strictly less than
. This particular branch has a number of useful additional properties:
- The standard branch
is holomorphic on its domain
.
- One has
for all
in the domain
. In particular, if
is real, then
is real.
- One has
for all
in the domain
.
One can then also use the standard branch of the logarithm to create standard branches of other multi-valued functions, for instance creating a standard branch of the square root function. We caution however that the identity
can fail for the standard branch (or indeed for any branch of the logarithm).
One can extend this standard branch of the logarithm to complex matrices, or (equivalently) to linear transformations
on an
-dimensional complex vector space
, provided that the spectrum of that matrix or transformation avoids the branch cut
. Indeed, from the spectral theorem one can decompose any such
as the direct sum of operators
on the non-trivial generalised eigenspaces
of
, where
ranges in the spectrum of
. For each component
of
, we define
where is the Taylor expansion of
at
; as
is nilpotent, only finitely many terms in this Taylor expansion are required. The logarithm
is then defined as the direct sum of the
.
The matrix standard branch of the logarithm has many pleasant and easily verified properties (often inherited from their scalar counterparts), whenever has no spectrum in
:
- (i) We have
.
- (ii) If
and
have no spectrum in
, then
.
- (iii) If
has spectrum in a closed disk
in
, then
, where
is the Taylor series of
around
(which is absolutely convergent in
).
- (iv)
depends holomorphically on
. (Easily established from (ii), (iii), after covering the spectrum of
by disjoint disks; alternatively, one can use the Cauchy integral representation
for a contour
in the domain enclosing the spectrum of
.) In particular, the standard branch of the matrix logarithm is smooth.
- (v) If
is any invertible linear or antilinear map, then
. In particular, the standard branch of the logarithm commutes with matrix conjugations; and if
is real with respect to a complex conjugation operation on
(that is to say, an antilinear involution), then
is real also.
- (vi) If
denotes the transpose of
(with
the complex dual of
), then
. Similarly, if
denotes the adjoint of
(with
the complex conjugate of
, i.e.
with the conjugated multiplication map
), then
.
- (vii) One has
.
- (viii) If
denotes the spectrum of
, then
.
As a quick application of the standard branch of the matrix logarithm, we have
Proposition 1 Let
be one of the following matrix groups:
,
,
,
,
, or
, where
is a non-degenerate real quadratic form (so
is isomorphic to a (possibly indefinite) orthogonal group
for some
. Then any element
of
whose spectrum avoids
is exponential, that is to say
for some
in the Lie algebra
of
.
Proof: We just prove this for , as the other cases are similar (or a bit simpler). If
, then (viewing
as a complex-linear map on
, and using the complex bilinear form associated to
to identify
with its complex dual
, then
is real and
. By the properties (v), (vi), (vii) of the standard branch of the matrix logarithm, we conclude that
is real and
, and so
lies in the Lie algebra
, and the claim now follows from (i).
Exercise 2 Show that
is not exponential in
if
. Thus we see that the branch cut in the above proposition is largely necessary. See this paper of Djokovic for a more complete description of the image of the exponential map in classical groups, as well as this previous blog post for some more discussion of the surjectivity (or lack thereof) of the exponential map in Lie groups.
For a slightly less quick application of the standard branch, we have the following result (recently worked out in the answers to this MathOverflow question):
Proposition 3 Let
be an element of the split orthogonal group
which lies in the connected component of the identity. Then
.
The requirement that lie in the identity component is necessary, as the counterexample
for
shows.
Proof: We think of as a (real) linear transformation on
, and write
for the quadratic form associated to
, so that
. We can split
, where
is the sum of all the generalised eigenspaces corresponding to eigenvalues in
, and
is the sum of all the remaining eigenspaces. Since
and
are real,
are real (i.e. complex-conjugation invariant) also. For
, the restriction
of
to
then lies in
, where
is the restriction of
to
, and
The spectrum of consists of positive reals, as well as complex pairs
(with equal multiplicity), so
. From the preceding proposition we have
for some
; this will be important later.
It remains to show that . If
has spectrum at
then we are done, so we may assume that
has spectrum only at
(being invertible,
has no spectrum at
). We split
, where
correspond to the portions of the spectrum in
,
; these are real,
-invariant spaces. We observe that if
are generalised eigenspaces of
with
, then
are orthogonal with respect to the (complex-bilinear) inner product
associated with
; this is easiest to see first for the actual eigenspaces (since
for all
), and the extension to generalised eigenvectors then follows from a routine induction. From this we see that
is orthogonal to
, and
and
are null spaces, which by the non-degeneracy of
(and hence of the restriction
of
to
) forces
to have the same dimension as
, indeed
now gives an identification of
with
. If we let
be the restrictions of
to
, we thus identify
with
, since
lies in
; in particular
is invertible. Thus
and so it suffices to show that .
At this point we need to use the hypothesis that lies in the identity component of
. This implies (by a continuity argument) that the restriction of
to any maximal-dimensional positive subspace has positive determinant (since such a restriction cannot be singular, as this would mean that
positive norm vector would map to a non-positive norm vector). Now, as
have equal dimension,
has a balanced signature, so
does also. Since
,
already lies in the identity component of
, and so has positive determinant on any maximal-dimensional positive subspace of
. We conclude that
has positive determinant on any maximal-dimensional positive subspace of
.
We choose a complex basis of , to identify
with
, which has already been identified with
. (In coordinates,
are now both of the form
, and
for
.) Then
becomes a maximal positive subspace of
, and the restriction of
to this subspace is conjugate to
, so that
But since and
is positive definite, so
as required.

24 comments
Comments feed for this article
4 May, 2015 at 1:36 am
Anonymous
It seems that the standard logarithm can be extended for a more general class of operators on a complex Banach space via its Cauchy integral formula representation (provided that the integration contour encloses the spectrum of
on a complex Banach space via its Cauchy integral formula representation (provided that the integration contour encloses the spectrum of  and avoids the branch cut).
and avoids the branch cut).
[Remark added – T.]
4 May, 2015 at 8:26 pm
Anonymous
In the Cauchy integral representation (property (iv) before proposition 1), the denominator in the integrand should be
in the integrand should be  (but it seems better to use the standard notation
(but it seems better to use the standard notation 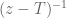 for the nonscalar resolvent of
for the nonscalar resolvent of  ).
).
[Corrected, thanks – T.]
4 May, 2015 at 5:30 am
Leo Stein
You currently have ${z\in \mathbb{C} : |\Im z| < \pi }$ in your definition of the standard branch of Log. I believe this is a typo, and you mean \arg instead of \Im
[The restriction on is on the range of Log, not the domain – T.]
is on the range of Log, not the domain – T.]
4 May, 2015 at 5:43 am
Jarred Barber
You have a minor typo in Prop 1: 0 <= k <= n-k should be 0 <= k <= n
[Corrected – T.]
4 May, 2015 at 6:01 am
Daniel
It may be good to remark that the standard branch (like any branch) of the logarithm also has one not so nice property: In general Log (zw) is not equal to Log z + Log w. For the multivalued function log it is true that log (zw) = log z + log w in the sense of (Minkowski) sum of sets.
[Remark added – T.]
4 May, 2015 at 8:27 am
Anonymous
The identity is satisfied for the standard branch near
is satisfied for the standard branch near  in
in  and therefore (by analytic continuation) also globally on the product of the corresponding domains (for
and therefore (by analytic continuation) also globally on the product of the corresponding domains (for  and
and 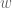 ) in
) in  .
.
4 May, 2015 at 10:17 am
Anonymous
Correction: In order to use the analytic continuation argument, the domains of and
and 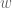 should be sufficiently restricted (e.g. to the open right half plane) so that their “productset” should be connected and not intersecting the branch line (i.e.
should be sufficiently restricted (e.g. to the open right half plane) so that their “productset” should be connected and not intersecting the branch line (i.e.  should be well defined).
should be well defined).
4 May, 2015 at 6:47 am
Anonymous
Since the standard logarithm is holomorphic on its domain, it is uniquely determined (via analytic continuation) by its value at any single point in the domain (e.g. at
at  ).
).
4 May, 2015 at 1:16 pm
Ben
Typo: you wrote Log(zw)=Log(z)Log(w).
[Corrected, thanks – T.]
4 May, 2015 at 3:55 pm
David Speyer
This choice of standard branch has the slightly odd property that, if is a Lie subgroup of
is a Lie subgroup of  , then
, then  may not land in the Lie algebra of
may not land in the Lie algebra of  . For example, if
. For example, if  is
is  , and
, and  has eigenvalues
has eigenvalues 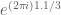 ,
, 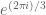 and
and 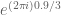 , then your logarithm will have eigenvalues
, then your logarithm will have eigenvalues  and hence trace
and hence trace 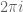 , not
, not  . Indeed, for
. Indeed, for  , I think your fundamental domain is disconnected, having three regions where the logarithm has trace
, I think your fundamental domain is disconnected, having three regions where the logarithm has trace  ,
,  and
and 
A while back I noticed a way to fix this for simply connected compact groups. Let be the Lie algebra. Let
be the Lie algebra. Let  be the set of
be the set of  such that the spectrum of
such that the spectrum of  lies in
lies in  . Then
. Then  is a convex neighborhood of the origin in
is a convex neighborhood of the origin in 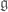 , and the exponential map
, and the exponential map  is an open immersion with dense image. In the
is an open immersion with dense image. In the  case, this means that we lift
case, this means that we lift 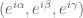 in the unique manner such that
in the unique manner such that 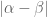 ,
,  and
and  and
and 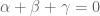 . For example, we lift
. For example, we lift  to
to  .
.
The argument I found went through a bunch of root system combinatorics, although I assume there is a simple explanation for it that I missed. I'd be curious whether people have seen this before.
4 May, 2015 at 7:08 pm
Allen Knutson
For a simply connected compact group, consider the composite where
where  is the coweight lattice and
is the coweight lattice and  the Weyl alcove. Now consider the preimage of the far wall of the Weyl alcove; I think your
the Weyl alcove. Now consider the preimage of the far wall of the Weyl alcove; I think your  is the connected component around
is the connected component around  of the complement.
of the complement.
Maybe this is the root system combinatorics you were talking about. Anyway yes, at least one person has seen it before.
5 May, 2015 at 6:52 am
David Speyer
Yup, that’s the root system combinatorics I was thinking about, although I phrased it differently in my mind.
5 May, 2015 at 10:55 pm
Lei Wang
About Proposition 3, what about lies in the other components of
lies in the other components of  ? I feel one can still show bounds on
? I feel one can still show bounds on  .
.
6 May, 2015 at 7:49 am
Terence Tao
It appears that the same argument gives either or
or 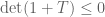 for any
for any  , where the sign of the inequality depends on whether the restriction (and projection) of
, where the sign of the inequality depends on whether the restriction (and projection) of  to a maximal totally positive subspace is orientation preserving or not.
to a maximal totally positive subspace is orientation preserving or not.
6 May, 2015 at 8:04 am
Lei Wang
There are four components in total, right ? Can one prove a stronger statement like in one (or even two) of the four ?
in one (or even two) of the four ?
6 May, 2015 at 8:08 am
Terence Tao
I believe this is the case when is odd. For instance, for odd
is odd. For instance, for odd  , the component of
, the component of  containing
containing  will necessarily have an odd number of eigenvalues at -1 (counted with algebraic multiplicity), since all nearby eigenvalues come in pairs
will necessarily have an odd number of eigenvalues at -1 (counted with algebraic multiplicity), since all nearby eigenvalues come in pairs  , and so
, and so  is necessarily zero on this component. (One way to think about this is that one inequality comes from considering the projection of
is necessarily zero on this component. (One way to think about this is that one inequality comes from considering the projection of  onto the totally positive space, and the other inequality comes from analysing the totally negative space. When
onto the totally positive space, and the other inequality comes from analysing the totally negative space. When  is even, it looks like both arguments give the same inequality rather than opposing inequalities.)
is even, it looks like both arguments give the same inequality rather than opposing inequalities.)
6 May, 2015 at 1:56 pm
Lei Wang
It appears to me this is independent of . In the
. In the  and
and 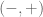 component one has
component one has 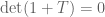 , while in the
, while in the  component
component  ;
;  component
component 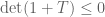 . Again, just an empirical observation plus some guesswork from a computational physicists :-)
. Again, just an empirical observation plus some guesswork from a computational physicists :-)
6 May, 2015 at 2:30 pm
Terence Tao
I think you are correct. In particular, is always singular on the
is always singular on the 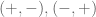 components. It would be interesting to have an elementary proof of this in the case when n is even (the argument I gave only worked then n is odd). It generalises the assertion that an orthogonal matrix of determinant -1 necessarily has an odd number of eigenvalues at -1 (because the product of all the other eigenvalues is positive), regardless of the parity of dimension.
components. It would be interesting to have an elementary proof of this in the case when n is even (the argument I gave only worked then n is odd). It generalises the assertion that an orthogonal matrix of determinant -1 necessarily has an odd number of eigenvalues at -1 (because the product of all the other eigenvalues is positive), regardless of the parity of dimension.
2 June, 2015 at 7:23 am
Gergely Harcos
Dear Lei, here is a direct argument that you asked for in our email correspondence. Assume that . Following the blog entry, we can assume that
. Following the blog entry, we can assume that  has no spectrum at
has no spectrum at  , for otherwise
, for otherwise 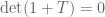 . Then,
. Then,
hence . Furthermore, the sign of
. Furthermore, the sign of 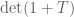 equals the sign of
equals the sign of  , which in turn equals
, which in turn equals 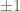 depending whether
depending whether  lies in the
lies in the  component or the
component or the  component. Done.
component. Done.
9 May, 2015 at 9:10 am
Anonymous
I share the assessment of:
therefore ;
; 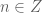 we have.
we have.
$latex e^{\frac{1+i \sqrt{n}}{n}} = e^{\frac{1}{n}}
15 May, 2015 at 3:28 am
Sign problems, Terry Tau, and open science | This Condensed Life
[…] For spin unpolarized systems it’s pretty clear why each A_i is of this form, but for others systems it’s not as clear. Anyways, this was the question he posed to mathoverflow. Amazingly people jumped on it, and it wasn’t long before Fields Medalist Terrance Tao got involved! It was then only a matter of 3 days before the conjecture was proven to be true in a mathematically rigorous way. For a full writeup of the proof, you can check out Tao’s blog. […]
31 May, 2015 at 9:48 am
E.L. Wisty
Reblogged this on Pink Iguana.
26 September, 2015 at 6:09 am
gninrepoli
There is a clear link between the natural logarithm, and trigonometric functions (cosine, sine, which are defined on the two-dimensional space). I have a question. Built on whether the model such as four-dimensional space? I mean the same functions for the study of the nature of prime numbers for example.Until I see the study of the same prime numbers only with a two-dimensional space.And I’m still interested in the nature of prime numbers in what space they are located? Maybe in the third? At least describe them by using the same two-dimensional space is difficult. Perhaps this is more a philosophy than mathematics.
26 September, 2015 at 6:25 am
gninrepoli
I mean the opening of a Cartesian system, and then the natural logarithm. Later there were complex numbers.