There is a very nice recent paper by Lemke Oliver and Soundararajan (complete with a popular science article about it by the consistently excellent Erica Klarreich for Quanta) about a surprising (but now satisfactorily explained) bias in the distribution of pairs of consecutive primes when reduced to a small modulus
.
This phenomenon is superficially similar to the more well known Chebyshev bias concerning the reduction of a single prime to a small modulus
, but is in fact a rather different (and much stronger) bias than the Chebyshev bias, and seems to arise from a completely different source. The Chebyshev bias asserts, roughly speaking, that a randomly selected prime
of a large magnitude
will typically (though not always) be slightly more likely to be a quadratic non-residue modulo
than a quadratic residue, but the bias is small (the difference in probabilities is only about
for typical choices of
), and certainly consistent with known or conjectured positive results such as Dirichlet’s theorem or the generalised Riemann hypothesis. The reason for the Chebyshev bias can be traced back to the von Mangoldt explicit formula which relates the distribution of the von Mangoldt function
modulo
with the zeroes of the
-functions with period
. This formula predicts (assuming some standard conjectures like GRH) that the von Mangoldt function
is quite unbiased modulo
. The von Mangoldt function is mostly concentrated in the primes, but it also has a medium-sized contribution coming from squares of primes, which are of course all located in the quadratic residues modulo
. (Cubes and higher powers of primes also make a small contribution, but these are quite negligible asymptotically.) To balance everything out, the contribution of the primes must then exhibit a small preference towards quadratic non-residues, and this is the Chebyshev bias. (See this article of Rubinstein and Sarnak for a more technical discussion of the Chebyshev bias, and this survey of Granville and Martin for an accessible introduction. The story of the Chebyshev bias is also related to Skewes’ number, once considered the largest explicit constant to naturally appear in a mathematical argument.)
The paper of Lemke Oliver and Soundararajan considers instead the distribution of the pairs for small
and for large consecutive primes
, say drawn at random from the primes comparable to some large
. For sake of discussion let us just take
. Then all primes
larger than
are either
or
; Chebyshev’s bias gives a very slight preference to the latter (of order
, as discussed above), but apart from this, we expect the primes to be more or less equally distributed in both classes. For instance, assuming GRH, the probability that
lands in
would be
, and similarly for
.
In view of this, one would expect that up to errors of or so, the pair
should be equally distributed amongst the four options
,
,
,
, thus for instance the probability that this pair is
would naively be expected to be
, and similarly for the other three tuples. These assertions are not yet proven (although some non-trivial upper and lower bounds for such probabilities can be obtained from recent work of Maynard).
However, Lemke Oliver and Soundararajan argue (backed by both plausible heuristic arguments (based ultimately on the Hardy-Littlewood prime tuples conjecture), as well as substantial numerical evidence) that there is a significant bias away from the tuples and
– informally, adjacent primes don’t like being in the same residue class! For instance, they predict that the probability of attaining
is in fact
with similar predictions for the other three pairs (in fact they give a somewhat more precise prediction than this). The magnitude of this bias, being comparable to , is significantly stronger than the Chebyshev bias of
.
One consequence of this prediction is that the prime gaps are slightly less likely to be divisible by
than naive random models of the primes would predict. Indeed, if the four options
,
,
,
all occurred with equal probability
, then
should equal
with probability
, and
and
with probability
each (as would be the case when taking the difference of two random numbers drawn from those integers not divisible by
); but the Lemke Oliver-Soundararajan bias predicts that the probability of
being divisible by three should be slightly lower, being approximately
.
Below the fold we will give a somewhat informal justification of (a simplified version of) this phenomenon, based on the Lemke Oliver-Soundararajan calculation using the prime tuples conjecture.
To explain the Lemke Oliver-Soundararajan bias, it is convenient to relax the requirement that the primes are consecutive, and just look at small prime differences
between primes
that are somewhat close (in the sense that
is of size
, which corresponds by the prime number theorem to the mean spacing between primes), but not necessarily consecutive. (This relaxation changes some of the constants in the Lemke Oliver-Soundarajaran analysis, basically by eliminating the need to invoke the inclusion-exclusion principle, but does not affect the qualitative nature of the bias.) The naive Cramér random model for the primes (discussed for instance in this post) suggests, as a first approximation, that for any
, the number of prime differences
that are equal to
with
should be on the order of
. Of course, this naive model is well known to require some adjustment: most obviously, prime differences
are almost always even, so the number of solutions to
is close to zero when
is odd. A little less obviously, values of
, such as
, which are multiples of three should (all other things being equal) be twice as likely to be prime differences as values of
(such as
) which are not; that is to say, one expects about twice as many “sexy primes” as “twin primes“. This is ultimately because the lower prime
in a sexy prime pair
can lie in either of the two residue classes
,
, but the lower prime
in a twin prime pair
can only lie in the residue class
(after excluding the first twin prime pair
).
The Lemke Oliver-Soundararajan bias pushes back against this phenomenon slightly; roughly speaking, it says that a typical number that is a multiple of
is only about
times as likely to be a prime difference as a typical number
that is a non-multiple of
, for some absolute constant
(which can be computed explicitly from their work, but I will not do so here).
This bias can be established assuming the Hardy-Littlewood prime tuples conjecture (with a sufficiently good error term). This conjecture asserts, roughly speaking, that the number of solutions to with
and some given even
is proportional to
, where
is the quantity
The proportionality constant depends on the implicit constants in the relation , and also involves the twin prime constant
it will not play an important role though in our analysis, so we omit it. The reason for the factor can be explained from the following simple calculation: if
is an odd prime, and we select two numbers
independently at random that are coprime to
(and equally likely to be in each of the
primitive residue classes mod
), then the probability that
can be calculated to be
times as large as the probability that
for any given
not divisible by
. For instance, if
, then
is twice as likely to equal
as it is equal
, as we have already observed before.
Naively, one would expect the quantity to be about twice as large when
is a multiple of three than when
is not a multiple of
, due to the
factor of
in (1). However, it turns out that when restricting to the range
, the average value of
for
a multiple of
is only about
as large as the average value of
for
not a multiple of
.
If we strip out the term in (1), creating a new function
then the previous bias turns out to be a consequence of an asymptotic roughly of the form
for some absolute constants and all
. (Actually, to avoid some artificial boundary issues one should replace the restriction
with a smoother weight such as
, but we will ignore this technicality for sake of discussion.) Indeed, assuming the asymptotic (2), we have
whereas
so we see that has a slightly lower mean (by a factor of about
) on the multiples of
than in general, which implies the corresponding claim about
. We thus see that the Lemke Oliver-Soundarajan bias can be traced to the lower order term
in (2).
In the paper of Lemke Oliver and Soundararajan, the asymptotic (2) (smoothed out as discussed above) is obtained from standard complex methods, based on an analysis of the Dirichlet series
As it turns out, this Dirichlet series has poles at both and
(it contains a factor of
), contributing to the
and
terms respectively. One can also establish (2) (with smoothing) using elementary number theory methods (as in this previous post); we sketch the argument as follows. We can factor
as a Dirichlet convolution
where vanishes unless
is the product of distinct primes greater than or equal to
, in which case
(with the convention ). Then we have
Morally speaking, behaves like
; we can use pseudorandomness heuristics to argue that the fluctuation around this main term give a lower order contribution (and one can argue this rigorously when using smoother weights like
). The term
can be interpreted as
, as per this previous post. Assuming this approximation, we obtain the approximation
The sequence behaves somewhat like
. As such, one expects (and can calculate)
to have an asymptotic of the form
, while
has an asymptotic of the form
for some explicit constants
, which gives (2).
Remark 1 One way of thinking about (2) is that the function
behaves on the average like
. The bulk of the bias effect is then coming from small values
of
, that is from prime gaps that are significantly smaller than average; one should not see the bias effect if one restricts to prime gaps of the typical size of
. This is consistent with the general philosophy that one does not expect to see “long-range” correlations between the primes.

81 comments
Comments feed for this article
14 March, 2016 at 5:05 pm
Biases between consecutive primes – jiangose
[…] https://terrytao.wordpress.com/2016/03/14/biases-between-consecutive-primes/ […]
14 March, 2016 at 8:15 pm
Asvin
I am not sure if the following question makes complete sense but do we expect a function field analogue for this phenomenon?
Consecutive primes no longer makes sense but perhaps one can ask what fraction of primes with degree < d+2 are in the same residue class or something along these lines?
Perhaps this is easier to prove?
15 March, 2016 at 8:56 am
Terence Tao
Yes, I think something along these lines can be proven, particularly if one works with differences of irreducible polynomials rather than trying to come up with a good notion of “consecutive” irreducible polynomials. In particular, the analysis given in this blog post, when translated to a finite field setting, seems to indicate that a low degree polynomial is a little bit less likely than naively expected to be the difference of two high degree irreducible polynomials
is a little bit less likely than naively expected to be the difference of two high degree irreducible polynomials 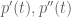 if
if  is divisible by a very small polynomial
is divisible by a very small polynomial  (where “naively expected” means what one would expect if
(where “naively expected” means what one would expect if 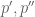 were random polynomials chosen to be coprime to
were random polynomials chosen to be coprime to  ).
).
14 March, 2016 at 9:16 pm
John Baez
The word “adjustement” should be adjusted to “adjustment”.
[Corrected, thanks – T.]
14 March, 2016 at 11:19 pm
Anonymous
It seems that in the ninth row below (2), the coefficient 3 in the RHS is not needed.
[Corrected, thanks – T.]
15 March, 2016 at 12:04 am
Anonymous
Is there any influence of this bias on the spacing between zeta zeros on the critical line?
15 March, 2016 at 8:50 am
Terence Tao
Interesting question. The Lemke Oliver-Soundararajan bias can be explained in terms of the prime tuples conjecture, which can also be used to explain (at least part of) the GUE hypothesis for spacings between zeroes (as per the work of Goldston and Montgomery on the pair correlation conjecture), so I would presume that this bias is consistent with the GUE hypothesis, for which we have quite a bit of numerical evidence and other supporting data.
15 March, 2016 at 2:58 am
Anonymous
Since this bias is implied by the prime tuples conjecture, does this means that the remainder term in the prime tuple conjecture is unbiased?
15 March, 2016 at 8:53 am
Terence Tao
The remainder term in the prime tuples conjecture is conjectured to be only the size of the main term, and so should not have any appreciable influence on the Lemke Oliver-Soundararajan bias, which is significantly larger (of size about
the size of the main term, and so should not have any appreciable influence on the Lemke Oliver-Soundararajan bias, which is significantly larger (of size about  of the main term). In particular, this remainder term could be heavily biased or significantly larger than expected and still it would not have a visible effect on the Lemke Oliver-Soundararajan bias (see also the remarks at the top of page 7 of their paper).
of the main term). In particular, this remainder term could be heavily biased or significantly larger than expected and still it would not have a visible effect on the Lemke Oliver-Soundararajan bias (see also the remarks at the top of page 7 of their paper).
15 March, 2016 at 9:30 pm
Michael D. Moffitt
I had thought Richard Brent proved something along these lines back in 1974 (“The Distribution of Small Gaps Between Successive Primes”).
Theorems aside, this result seems to hold trivially – maybe I am missing something? For instance, the pop science article implies that one would expect the last digit of a successive prime to be randomly distributed. Why would anyone assume this? If p is prime, surely p + 6 has a greater chance of being prime than p + 10 (since p + 10 has the chance of landing on a multiple of 3, whereas p + 6 cannot).
Is there something more to this?
16 March, 2016 at 12:53 am
Anurag Sahay
Yes. The bias that you’d expect from this phenomenon is not as large as the actual observed bias.
16 March, 2016 at 1:06 am
Michael D. Moffitt
Ah, ok. In the paper, the authors purport an expectation that one should expect *equally* occurring residue pairs. I don’t see how that can be reconciled with the known distribution of prime gaps … especially in Base 10, it appears that the “p + 6” peak explains away a majority of the differences in occurrence.
16 March, 2016 at 1:00 am
Michael D. Moffitt
I should have phrased my question this way: given that the distribution of prime gaps is well-known to be highly multimodal (with peaks at 6 & 12, dips at 8, etc.), wouldn’t it have taken a miracle for all pairwise residues to occur at identical frequencies in the first place? I would never have expected a uniform distribution to begin with.
16 March, 2016 at 9:15 am
Terence Tao
The precise phrase used by the authors (at the bottom of page 1) is “roughly equally often”. (The modifier “roughly” makes a crucial distinction, analogous to the distinction between the law of large numbers and the gambler’s fallacy.) The surprise is not that there exist some biases in the distribution, but that the quantitative magnitude of the bias is so large. As mentioned in the post, the Chebyshev bias, for instance, only explains about of the bias, and irregularities in small prime gaps such as
of the bias, and irregularities in small prime gaps such as 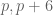 , or the simple fact that after a given residue class (such as
, or the simple fact that after a given residue class (such as 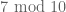 ), one has to wait longer for the next appearance of that class than any other class, can explain a further
), one has to wait longer for the next appearance of that class than any other class, can explain a further  of the gap, but what was unexpected was that the bias was even larger than that, being proportional to
of the gap, but what was unexpected was that the bias was even larger than that, being proportional to  . This indicates that there are some systematic biases in prime gaps at moderately large scales, which in my blog post is captured by the terms involving the factor
. This indicates that there are some systematic biases in prime gaps at moderately large scales, which in my blog post is captured by the terms involving the factor 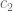 . This can be compared with the classical computation of Gallagher on the average behaviour of prime gaps, which in the language of the blog post roughly corresponds to the asymptotic
. This can be compared with the classical computation of Gallagher on the average behaviour of prime gaps, which in the language of the blog post roughly corresponds to the asymptotic  . The surprise is then the extra
. The surprise is then the extra  term appearing in the finer asymptotic in (2).
term appearing in the finer asymptotic in (2).
One way to think about the Lemke Oliver-Soundararajan bias is the following. The Cramer type models suggest that the distribution of the prime differences should be distributed according to the difference between two randomly selected residue classes coprime to
should be distributed according to the difference between two randomly selected residue classes coprime to  . On the other hand, the diagonal case
. On the other hand, the diagonal case  gives a somewhat large contribution to the
gives a somewhat large contribution to the  difference. To balance this, the other prime differences should have some additional slight bias away from
difference. To balance this, the other prime differences should have some additional slight bias away from  . This bias is indeed slight – prime differences of magnitude
. This bias is indeed slight – prime differences of magnitude 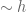 will exhibit a bias of about
will exhibit a bias of about  due to this redistribution – but after summing over all
due to this redistribution – but after summing over all  , this creates the additional
, this creates the additional 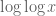 increase in bias over the effects of size
increase in bias over the effects of size  coming from more readily apparent bias effects. To put it another way, there is a form of the gambler’s fallacy that is actually valid for the distribution of primes in residue classes!
coming from more readily apparent bias effects. To put it another way, there is a form of the gambler’s fallacy that is actually valid for the distribution of primes in residue classes!
18 March, 2016 at 8:43 am
Anonymous
Sorry Terry, but I just don’t buy the “roughly equal” premise either – it’s a straw man argument. If I were a classically trained mathematician (which I’m not), I’d base my initial expectations on the known, *observed* distribution of consecutive primes, not Cramer’s bogus random model. The “Jumping Champions” paper from 1999 plots a nice distribution up to N = 100000.
p(gap=2): 10.25%
p(gap=4): 10.21%
p(gap=6): 16.25%
p(gap=8): 7.07%
…
The transition probabilities between residue classes of any distance (in any base!) can be computed directly from these. For mod 3, the gaps that retain residue classes occur at sizes of 6, 12, etc. All the others lead to external transfers:
p(same_residue) = p(gap=6) + p(gap=12) + … = 0.42
p(diff_residue) = p(gap=2) + p(gap=4) + … = 0.58
There’s your bias factor right there – *by inspection*, one would expect transitions to a different residue class almost 50% more often, and that’s exactly what we see. So, I simply don’t understand why this suddenly comes as a surprise to the math elites.
Perhaps number theorists never bothered to read these decades-old papers? If so, I think that’s the real news here. If I were to write a headline for this breakthrough, it would be “Theoretical Mathematicians Discover Computers.”
18 March, 2016 at 9:38 am
Anonymous
It seems like you’re focusing on “small numbers”. The numerical evidence can be explained via these gaps, but what about for very large n? The distribution of the gaps is different. For example, the most common gap should be around log n. If n is much larger, then your common gaps are not 2, 4, 6, 8, but numbers near log n. As Tao already pointed out, the frequency of certain gaps explains part of the bias, but the bias is even larger than what would come from just looking at the gaps.
18 March, 2016 at 10:03 am
Anonymous
You’ve got it wrong. The *average* gap size is log(n), but the *most common* gap size is 6 … all the way up to 10^35 (please read the 1999 Jumping Champions paper). Small gaps dominate the distribution for a long, long time!
My claim is that you can *exactly* predict the bias just by counting up the gap frequencies. Try it for yourself! Write a program that keeps track of the gap sizes (feel free to go as high as you want) and then add up the gap sizes that are multiples of 6. You will see the bias term right there, plain as day.
18 March, 2016 at 12:58 pm
Terence Tao
The 9:38am poster is correct. Small gaps such as 6 may be the most frequently occurring gap for some time, but even this gap only actually occurs about of the time, and these small gaps only explain at most
of the time, and these small gaps only explain at most  of the bias effect at most. As I said previously, the surprise is not that the bias effect exists at all, but that it is larger than the
of the bias effect at most. As I said previously, the surprise is not that the bias effect exists at all, but that it is larger than the  effect caused by individual prime gap sizes such as 6, instead being of size
effect caused by individual prime gap sizes such as 6, instead being of size 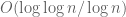 . It is this extra
. It is this extra 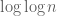 factor which was not predicted in any of the previous numerical work on the problem (indeed, it would be difficult to see this term even for
factor which was not predicted in any of the previous numerical work on the problem (indeed, it would be difficult to see this term even for  as large as
as large as  ), and in my opinion this is the most interesting aspect of the Lemke Oliver-Soundararajan work. (Interestingly, if one works with the conjectural “jumping champion”, which is usually the primorial close to
), and in my opinion this is the most interesting aspect of the Lemke Oliver-Soundararajan work. (Interestingly, if one works with the conjectural “jumping champion”, which is usually the primorial close to 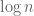 , one gets an effect of size about
, one gets an effect of size about 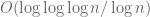 , but in the wrong direction – the jumping champion tends to be divisible by all small primes and so would presumably bias the prime gaps to favour being divisible by such primes, rather than away from it. So the Lemke Oliver-Soundararajan effect is actually strong enough to counteract the effect of jumping champions!)
, but in the wrong direction – the jumping champion tends to be divisible by all small primes and so would presumably bias the prime gaps to favour being divisible by such primes, rather than away from it. So the Lemke Oliver-Soundararajan effect is actually strong enough to counteract the effect of jumping champions!)
Incidentally, there are many other examples in the analytic number theory literature in which numerical evidence ended up being misleading due to an inability to see contributions of order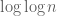 or slower. Examples include Mertens’ conjecture (known to fail before about
or slower. Examples include Mertens’ conjecture (known to fail before about 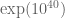 or so), the conjecture
or so), the conjecture  (known to fail at or before Skewes’ number), and the second Hardy-Littlewood conjecture (suspected to fail before
(known to fail at or before Skewes’ number), and the second Hardy-Littlewood conjecture (suspected to fail before  ). On the other hand, all numerical evidence available still points to these conjectures being true; it is only theoretical calculations that can discern the true asymptotic behaviour (though in some cases the results are conditional on standard conjectures such as the Riemann hypothesis or the prime tuples conjecture). As such, we’ve learned not to rely solely on numerical evidence, even if it involves a superficially impressive number of data points (e.g.
). On the other hand, all numerical evidence available still points to these conjectures being true; it is only theoretical calculations that can discern the true asymptotic behaviour (though in some cases the results are conditional on standard conjectures such as the Riemann hypothesis or the prime tuples conjecture). As such, we’ve learned not to rely solely on numerical evidence, even if it involves a superficially impressive number of data points (e.g.  ); far more convincing would be a combination of numerical evidence and theoretical results showing that the numerically observed phenomenon can be derived from, or is at least consistent with, existing theorems and standard heuristic models and conjectures such as the Riemann hypothesis, the prime tuples conjecture, or the Cramer model (which are in turn supported not only by numerics, but by a vast array of theoretical partial results and other evidence).
); far more convincing would be a combination of numerical evidence and theoretical results showing that the numerically observed phenomenon can be derived from, or is at least consistent with, existing theorems and standard heuristic models and conjectures such as the Riemann hypothesis, the prime tuples conjecture, or the Cramer model (which are in turn supported not only by numerics, but by a vast array of theoretical partial results and other evidence).
[EDIT: the effect of the jumping champion is in fact , not
, not  as previously claimed. -T.]
as previously claimed. -T.]
18 March, 2016 at 10:35 pm
Anonymous
It is not clear why the “jumping champion” effect is missing in conjecture 1.1 in the paper (which has a smaller second order term of size ).
).
20 March, 2016 at 7:48 am
Terence Tao
It smooths out. It is true that technically, the existence of jumping champions (or more generally, the unbounded nature of makes the estimate (2) false as stated, but if one uses the smooth weight of
makes the estimate (2) false as stated, but if one uses the smooth weight of 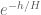 (which corresponds to the actual distribution of prime gaps, which is conjecturally exponential with mean
(which corresponds to the actual distribution of prime gaps, which is conjecturally exponential with mean  ). Unlike rough sums, a smooth sum can have error terms that are smaller than the size of an individual term. For instance,
). Unlike rough sums, a smooth sum can have error terms that are smaller than the size of an individual term. For instance,  has error terms that can be made smaller than any given power of
has error terms that can be made smaller than any given power of  by suitable Taylor expansion.
by suitable Taylor expansion.
20 March, 2016 at 9:04 am
Anonymous
It seems that the summands in the above example should be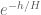 .
.
[Corrected, thanks – T.]
16 March, 2016 at 2:53 am
¿Sorpresa sobre los números primos? | Ciencia | La Ciencia de la Mula Francis
[…] Para entender mi sorpresa, te recomiendo leer a Alvy (@Alvy), “Descubierto un extraño comportamiento de los números primos que se «repelen»”, Microsiervos, 14 Mar 2016. Luego pasar a su fuente, Erica Klarreich, “Mathematicians Discover Prime Conspiracy,” Quanta Magazine, 13 Mar 2016. Para luego leer las cuatro primeras páginas (el resto no merece la pena) de Robert J. Lemke Oliver, Kannan Soundararajan, “Unexpected biases in the distribution of consecutive primes,” arXiv:1603.03720 [math.NT]. Y, finalmente, disfrutar con el genial Terry Tao, “Biases between consecutive primes,” What’s new, 14 Mar 2016. […]
16 March, 2016 at 4:01 am
Anonymous
For fixed small modulus and moderately large
and moderately large  , is there any known efficient method to evaluate the number of such pairs of consecutive primes (in two given residue classed mod
, is there any known efficient method to evaluate the number of such pairs of consecutive primes (in two given residue classed mod  ) in
) in ![[x, x+H]](https://s0.wp.com/latex.php?latex=%5Bx%2C+x%2BH%5D&bg=ffffff&fg=545454&s=0&c=20201002) for large x? (this may help in extending the range of the tables in the paper),
for large x? (this may help in extending the range of the tables in the paper),
16 March, 2016 at 8:05 am
Number Theory News | Not Even Wrong
[…] more details, there’s an excellent blog post from Terry Tao. This might be a good time to point out that people sometimes complain about the quality of […]
16 March, 2016 at 8:50 am
Ανακαλύφθηκε μια «περίεργη» ιδιότητα των πρώτων αριθμών | physicsgg
[…] Prime Conspiracy« 2. http://www.nature.com: «Peculiar pattern found in ‘random’ prime numbers» 3. terrytao.wordpress.com: «Biases between consecutive […]
16 March, 2016 at 3:04 pm
geometriclanglander
Simply wonderful. I wonder whether it provides an alternative vantage point when considering pair-correlation-esque random matrix analogies…
Unfortunately the comments are being overrun by a crank…
17 March, 2016 at 2:40 pm
Terence Tao
The excessive comments (14 in all) have now been removed as per the “spam” policy of my blog: https://terrytao.wordpress.com/about/
16 March, 2016 at 7:21 pm
Anonymous
Get a load of this: in the original version of the paper (at http://arxiv.org/pdf/1603.03720v1.pdf), they omitted a key reference to Ash et al. 2010. Why is that reference important? Because *they* are the ones that disclose this anti-pattern.
Now for the kicker: Soundararajan (one of the authors) was a reviewer for that paper! Look the the acknowledgements section:
Click to access ABGS-PrimePairsFinal.pdf
Terry, I’m curious if it’s typical for mathematicians to be this snakey.
16 March, 2016 at 9:18 pm
Terence Tao
I think Hanlon’s razor applies here. We try our best to collect the relevant references for a given paper, but the literature is vast, and sometimes papers slip through the cracks, though nowadays one often gets notified of a missing reference once we put a preprint up on the arXiv, or during the refereeing process. The 2011 paper of Ash et al. you mention, for instance, had zero citations in MathSciNet (though this will of course change when the current paper is published), so it may have been missed by the authors during their search of the literature. (This sort of thing happens quite often; just a few days ago, for instance, I updated my most recent preprints on the arXiv to add some references that Van and I missed, and were only pointed out to us after we released our first version of the preprints.)
It may be in a few years that semantic search tools become available that allow one to find the relevant literature more systematically (beyond the current method of relying on some ad hoc mix of literature searches, citation searches, consulting with other experts, one’s own memory, and use of general-purpose search engines like Google), but we’re not quite there yet.
Looking at the paper of Ash et al., it seems that Sound was credited for “help”, but was not a referee (and in mathematics, referees are generally anonymous and not disclosed to the authors). My guess is that the authors asked Sound a mathematical question related to their paper in the course of their research, but he might not have read or even seen the final version of the paper. (I myself get a couple such queries each week, and would probably not recall any specific such query dating back from 2010 or so unless I went back through my email archives to locate it.)
In any event, the Ash et al. paper is focusing on a slightly different aspect of the statistics of residue classes of consecutive primes, namely a certain conjectural “antidiagonal symmetry” predicted by their heuristics (and which is also predicted by the Lemke Oliver-Soundararajan computations, which are based on a slightly different heuristic model). They tentatively raise the possibility of a bias away from equal residue classes in the final section of their paper, but it is not strongly emphasised. According to their own paper as well as the Quanta article, the proximate inspiration for Lemke Oliver and Soundararajan was instead a lecture by Tadashi Tokieda on biases regarding the first occurrence of various patterns in coin tosses.
17 March, 2016 at 2:54 pm
kodlu
From the paper:
<< We give two other amusing consequences of Conjecture 1.1. The famous biases π(x) <
li(x), or π(x; 3, 1) < π(x; 3, 2), or π(x; 4, 1) < π(x; 4, 3) are known to be false infinitely
often. However we conjecture that the robust biases in pairs of consecutive primes (mod 3)
or (mod 4) may hold always and from the very start!
Conjecture 1.3: Let q = 3 or 4, and let a be either 1 (mod q) or −1 (mod q). Then for all
x ≥ 5, we have π(x; q,(a, -a)) > π(x; q,(a, a)). >>
Is it possible to envision a direct proof of Conjecture 1.3, without proving the much tougher Conjecture 1.1? How might one go about such a proof?
17 March, 2016 at 3:30 pm
Terence Tao
This conjecture looks well beyond the reach of current methods. For instance I think it is not currently known (though it is almost certainly true) that π(x; 4,(1, 3)) is >>π(x) (though, perversely, thanks to recent work of Maynard, we can prove this claim for the quantity π(x; 4,(1, 1)), which is supposed to be smaller!).
17 March, 2016 at 3:01 pm
Aubrey de Grey
I have a question: can this bias be expressed interestingly in terms of n rather than x? I ask because I just had a look at the phenomenon empirically, using the following very lazy Mathematica code:
k = 1000000;
w = 10000;
p1 = Table[Mod[Prime[n + 1] – Prime[n], 3], {n, 1, k + w}];
Show[Plot[0.5 – 0.25*Log[Log[n]]/Log[n], {n, 30, k},
PlotStyle -> Red, PlotRange -> Full],
ListPlot[Table[
Count[p1[[m – w ;; m + w]], 0]/(2 w + 1), {m, w + 1, k}]],
PlotRange -> {{1, k}, {0.4, 0.44}}]
which shows in red the expected probability of p_{n+1}-p_n being divisible by 3 according to this result, and in blue the proportion of the primes p_n-5000 through p_n+5000 for which p_{n+1}-p_n is in fact divisible by 3 – but, plotted with the x-axis scaled according to n rather than x. It’s no surprise that the error term is now O(1) rather than O(1/log x), but I’m wondering whether the actual value of that error term, which seems to hold pretty steady at about -0.017, can be derived from reasoning analogous to that of Lemke Oliver and Soundararajan.
17 March, 2016 at 3:28 pm
Terence Tao
Asymptotically, the prime number theorem tells us that , so the relationship between
, so the relationship between  and
and  is approximately
is approximately  , which implies that
, which implies that  and
and  . So, up to lower order terms, the size of the Lemke Oliver-Soundararajan bias should look about the same asymptotically whether viewed in terms of n or of x.
. So, up to lower order terms, the size of the Lemke Oliver-Soundararajan bias should look about the same asymptotically whether viewed in terms of n or of x.
18 March, 2016 at 3:12 am
Anonymous
It seems that the relatively large size of these biases (between consecutive primes) can be used to construct an explicit(!) statistical test to distinguish (almost surely!) the sequence of primes from any random sequence of “primes” constructed using standard probabilistic models for primes.
19 March, 2016 at 6:17 pm
kodlu
Can you clarify what you mean a bit further, this seems like an interesting idea.
20 March, 2016 at 12:09 am
Anonymous
Based on conjecture 1.1 in the paper, choose and
and  such that
such that 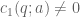 and define
and define

By conjecture 1.1, tends (as
tends (as 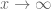 ) to the nonzero(!) limit
) to the nonzero(!) limit  for the sequence of primes, while it seems to tend almost surely (as having only the Chebyshev bias) to zero(!) for any sequence of “primes” constructed by standard probabilistic models for the primes.
for the sequence of primes, while it seems to tend almost surely (as having only the Chebyshev bias) to zero(!) for any sequence of “primes” constructed by standard probabilistic models for the primes.
18 March, 2016 at 5:34 am
Anonymous
It seems that such a test works even when a positive fraction (not 1) of the “primes” are primes!
18 March, 2016 at 2:05 pm
Alastair
I’m trying to understand intuitively what’s going on, in particular why the function is slightly smaller on average on the multiples of 3. This function is large precisely when
is slightly smaller on average on the multiples of 3. This function is large precisely when  has lots of small prime factors, not counting 3. If
has lots of small prime factors, not counting 3. If  is divisible by 3 then, since the 3 doesn’t count, we’re effectively looking at a number of size
is divisible by 3 then, since the 3 doesn’t count, we’re effectively looking at a number of size  so we should expect slightly fewer prime factors and hence a slightly smaller
so we should expect slightly fewer prime factors and hence a slightly smaller  . The average number of prime factors only changes from
. The average number of prime factors only changes from 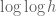 to
to  , which really doesn’t seem like very much although perhaps its enough to see why there’s a bias. I suspect that such crude heuristics, only looking at the average number of prime factors, aren’t powerful enough to predict the precise quantitative form of the bias.
, which really doesn’t seem like very much although perhaps its enough to see why there’s a bias. I suspect that such crude heuristics, only looking at the average number of prime factors, aren’t powerful enough to predict the precise quantitative form of the bias.
18 March, 2016 at 5:03 pm
Terence Tao
The way I think of it is as follows: given a random number between and
and  , the probability of being divisible by
, the probability of being divisible by  is not quite
is not quite 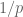 , but is slightly less – it is
, but is slightly less – it is  , which is roughly
, which is roughly  on the average. (The term
on the average. (The term  here can also be interpreted as
here can also be interpreted as  , analogous to the more infamous
, analogous to the more infamous  .) On the other hand, the probability that a random multiple of 3 between
.) On the other hand, the probability that a random multiple of 3 between  and
and  is divisible by
is divisible by  is slightly lower, about
is slightly lower, about  . More generally, given any
. More generally, given any  coprime to 3, the probability that a random number from
coprime to 3, the probability that a random number from  to
to  is divisible by
is divisible by  goes down by a slight amount (proportional to
goes down by a slight amount (proportional to  ) if we condition to multiples of 3. This is what biases the function
) if we condition to multiples of 3. This is what biases the function  downward by about
downward by about  on average if we restrict
on average if we restrict  to be a multiple of 3.
to be a multiple of 3.
Another way of thinking about it is that is divisible by
is divisible by  , so this leaves slightly fewer multiples of
, so this leaves slightly fewer multiples of  remaining for the non-zero numbers; when restricting to the multiples of three, the biasing effect of
remaining for the non-zero numbers; when restricting to the multiples of three, the biasing effect of  is larger, because it is a larger proportion of the total population of numbers available.
is larger, because it is a larger proportion of the total population of numbers available.
18 March, 2016 at 7:05 pm
John Baez
To me the most surprising thing about this discovery of Lemke Oliver and Soundararajan is that it wasn’t made earlier, perhaps even by an amateur number theorist who was good at computing. (Explaining the effect requires expertise, but discovering it seems much easier.)
So, why wasn’t it discovered sooner? My guess is that a whole class of questions has been insufficiently studied, of which this is the simplest. Unfortunately, I’m not quite sure what this class is.
I imagine this class includes simple variants like “if the nth prime equals a mod m and the (n+1)st prime equals b mod m, what is the probability that the (n+2)nd equals c mod m, given that n < N?"
But maybe someone who knows more number theory can better delineate this class of questions people forgot to ask, and find some of the more interesting questions in this class.
18 March, 2016 at 7:59 pm
Terence Tao
There were at least two papers in experimental number theory that noticed some manifestation of the Lemke Oliver-Soundararajan bias on a qualitative level: a 2011 paper of Ash, Beltis, Gross, and Sinott, and a 2002 paper of Ko. But I think the difficult task was to separate this bias from previously known biases in the distribution of the primes, such as the Chebyshev bias discussed in the blog post, or biases arising from the prime tuples conjecture (which, for instance, predicts that a prime gap of 6 is twice as likely to occur as a prime gap of 2). To realise that this particular bias is significantly stronger than what can be easily explained from these previously identified biases seems to require a certain amount of theoretical mathematical training.
22 March, 2016 at 8:07 am
John Baez
The paper by Lemke Oliver and Soundararajan starts with some striking facts like this: of the first hundred million primes, 25.000401% end in 7 in base ten. That’s very close to 1/4, which seems to make sense… but if one of these primes ends in 7, the probability that the next one ends in 7 is just 17.757%!
This is the sort of thing that an amateur with good computer skills could probably notice. I had thought this was a new observation. I’ll have to look at those other papers.
23 March, 2016 at 7:58 am
Terence Tao
The first hundred million primes occupy about 12% of the numbers up to 2 billion that end in 1, 3, 7, or 9 (discarding the tiny primes 2 and 5). If they were distributed randomly amongst this set, the probability that a prime ending in 7 would be followed next by another prime ending in 7 would be about
ending in 7 would be followed next by another prime ending in 7 would be about  , which is already significantly less than 25%, basically because the next numbers after
, which is already significantly less than 25%, basically because the next numbers after  that end in 9, 1, or 3 get to “go first” and have a chance of being prime before the next number
that end in 9, 1, or 3 get to “go first” and have a chance of being prime before the next number  ending in 7 needs to be tested. An amateur who observes the somewhat stronger 17% bias without doing something like the above quantitative calculation (or at least benchmarking the prime number statistics against a suitable random model) may end up ascribing the bulk of the bias to this effect (which, according to the Quanta article, is what Sound and Lemke Oliver did also, before working out the theoretical calculations more carefully).
ending in 7 needs to be tested. An amateur who observes the somewhat stronger 17% bias without doing something like the above quantitative calculation (or at least benchmarking the prime number statistics against a suitable random model) may end up ascribing the bulk of the bias to this effect (which, according to the Quanta article, is what Sound and Lemke Oliver did also, before working out the theoretical calculations more carefully).
25 March, 2016 at 5:22 am
arch1
Aside – that formula looks tweakable to compute each player’s likelihood of winning a round robin “Bernoulli trial” contest involving n players of different skill levels.
27 December, 2016 at 3:52 am
Julie
Your reasoning is not correct. It is a mistake to considerate the sequence 1, 3, 7, 9 … as an order to calculate the probability for the next prime.
You have to reject all multiples of 2, 3 and 5 before doing a theoretical calculation.
If you take 11, 41, 71… Next odd which will have a chance to be a prime will be 13, 43, 93
But if you take 31, 61, 91… the next odd which will have a real chance to be prime will be 37, 67, 97
So ais last digit is 1, the first number you have to considerate is 3 or 7.
Write numbers from 1 to 30 by excluding all miltiples of 2, 3 and 5. You’ll obtain this order for the last digit
1-7-1-3-7-9-3-9
So for each 7 (or any last digit) you have 2 possible ranks for the next 7.
First 7: 3rd and 8th
Second 7: 5th and 8th
Now i do the same quantitative calculation than you:
1 hundred million primes, 2 billion numbers, about 19% are prime
If we calculate each probality, we obtain:
(1, 1)≈ 18.9%
(1, 3)≈ 29.5%
(1, 7)≈ 30.5%
(1, 9)≈ 21.1%
(3, 1)≈ 24%
(3, 3)≈ 18.1%
(3, 7)≈ 27.4%
(3, 9)≈ 30.5%
(7, 1)≈ 25.2%
(7, 3)≈ 27.1%
(7, 7)≈ 18.1%
(7, 9)≈ 29.5%
(9, 1)≈ 31.9%
(9, 3)≈ 25.2%
(9, 7)≈ 24%
(9, 9)≈ 18.9%
Same approximate calculation in base 3 with the first million primes:
π(x; 3,(1, 1)) ≈ 219311
π(x; 3,(1, 2)) ≈ 280619
π(x; 3,(2, 1)) ≈ 280619
π(x; 3,(2, 2)) ≈ 219311
If we compare to numerical data, i think we can ascribe the bulk of the bias to this effect.
28 April, 2017 at 8:34 am
Terence Tao
Well, this analysis is not correct either – one has to reject multiples of 7 also. Then 11, then 13… but then it does indeed seem that this sequence of not-quite-correct predictions does converge fairly rapidly to the numerical data. In fact, this is basically the analysis that Lemke Oliver and Soundararajan actually do (they rely on the Hardy-Littlewood prime tuple conjecture, which roughly speaking asserts that the above sequence of not-quite-correct analyses do converge rapidly to the true statistics).
As mentioned before, though, the real surprise is that the cumulative bias effect of taking into account the rejection of multiples of 7, 11, 13, etc. is a little bit larger (by a factor of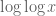 or so) from the effect of taking into account just a bounded number of primes such as 2, 3, 5. This
or so) from the effect of taking into account just a bounded number of primes such as 2, 3, 5. This 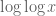 amplification of the bias is not really visible at numerically computable ranges such as
amplification of the bias is not really visible at numerically computable ranges such as  , but would eventually become significant for far larger values of
, but would eventually become significant for far larger values of  .
.
19 March, 2016 at 12:18 am
Prime Numbers Conspiracy | Financial Cryptography, Bitcoin, Crypto Currencies, Cryptanalysis
[…] used in Quanta Magazine paper about this. We stress that this bias though very substantial is now apparently satisfactorily explained ny […]
21 March, 2016 at 4:33 am
Dan Carmon
In this analysis you relaxed the consecutive-prime condition to a close-prime condition. A bias is still exhibited, but how much is lost in the transition?
The loss is perhaps not immediately clear when considering distributions of two consecutive / close primes, as both methods predict that the main term in the bias for (a,b) would be determined by whether a and b are congruent modulo q, or not.
However, when considering distributions of triples, this does not seem to be the case (at least as far as I understand it). When discussing close primes, it seems you should not be able to distinguish their order, so the main term for the biases for triplets of residues modulo 3 being (1,2,1), (1,1,2) and (2,1,1) should all be the same. However, Lemke Oliver-Soundararajan’s paper predicts that these distributions for consecutive primes should have quite different main terms – specifically, the adjacent 1’s should repel more forcefully than the distant 1’s (which do contribute to the secondary term, but not to the main
term, but not to the main 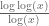 term.)
term.)
Do you have further thoughts on this? Am I wrong in the assertion that the close-primes analysis cannot distinguish between (1,2,1) and (2,1,1)?
Another way to phrase this question, perhaps simpler to model – the analysis of Lemke Oliver-Soundararajan predicts that the distribution of modulo 3 should be biased against (1,1) and (2,2), but this bias should be significantly smaller than the bias of the distribution of
modulo 3 should be biased against (1,1) and (2,2), but this bias should be significantly smaller than the bias of the distribution of 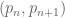 , only exhibiting
, only exhibiting  bias rather than the
bias rather than the 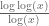 bias. Is this the behaviour predicted by a close-primes model for
bias. Is this the behaviour predicted by a close-primes model for  , or would that model again predict a bias with a large order of magnitude?
, or would that model again predict a bias with a large order of magnitude?
21 March, 2016 at 8:57 am
Terence Tao
I haven’t gone through the details of the Lemke Oliver-Soundararajan inclusion-exclusion analysis, but my guess is this: when looking at prime differences rather than prime gaps, one sees that most of the bias is coming from smallish size prime differences – where
– where  is much larger than 1, but much less than the average gap size
is much larger than 1, but much less than the average gap size  (as this is where the bulk of the
(as this is where the bulk of the 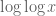 factor coming from summing the harmonic series
factor coming from summing the harmonic series 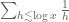 will come from). Now, such smallish prime differences are quite unlikely to have a third prime between them (as a first approximation, the probability of such an intervening prime should be roughly
will come from). Now, such smallish prime differences are quite unlikely to have a third prime between them (as a first approximation, the probability of such an intervening prime should be roughly  ). So the Lemke Oliver-Soundarajan effect should be significantly attenuated when trying to control the event that
). So the Lemke Oliver-Soundarajan effect should be significantly attenuated when trying to control the event that  and
and  have the same residue class, as it is quite unlikely that these two primes are so close together that the bulk of that effect applies. However, the event that (say)
have the same residue class, as it is quite unlikely that these two primes are so close together that the bulk of that effect applies. However, the event that (say)  and
and  have the same residue class is not subject to this repulsion effect.
have the same residue class is not subject to this repulsion effect.
24 March, 2016 at 1:50 am
Dan Carmon
Thank you for the great answer! My understanding is that the main contribution to the bias for prime differences therefore actually arises solely (up to lower order terms) from differences that are actually prime gaps: Differences which are not much smaller than , as well as differences which are much smaller than
, as well as differences which are much smaller than  but are not prime gaps, both contribute only to the
but are not prime gaps, both contribute only to the 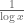 term, at the most. For the first family the contribution is small due to the size of the differences, while for the second family the contribution is small due to the rarity of such differences.
term, at the most. For the first family the contribution is small due to the size of the differences, while for the second family the contribution is small due to the rarity of such differences.
It seems plausible to me that smallish prime differences which are not primes gaps are responsible for the part of in Lemke Oliver-Soundararajan’s conjecture which resembles the main
in Lemke Oliver-Soundararajan’s conjecture which resembles the main 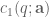 part, namely
part, namely  . Does this seem reasonable?
. Does this seem reasonable?
Have you explored the Lemke Oliver-Soundararajan paper further since? Specifically, are you able to determine that the bias that arises in their computations is similarly dominated by the contribution of smallish primes gaps?
21 March, 2016 at 6:56 am
A. Mehta
Thanks for the interesting and insightful analysis as always, Terence.
One question: a previous poster mentioned the 1974 paper by RP Brent that predicts gap sizes between consecutive primes — which, although not cited by the authors, employs Hardy-Littlewood and seems highly relevant either way. Should we expect a different magnitude of bias to be produced by that model?
The reason I ask is because the predicted distribution in that paper (shown in Table 2 for small AND large gap sizes) appears to exhibit a FAR greater systematic bias than what you suggest. To be specific: you say that we should expect gap multiples of 6 roughly twice as often as those that aren’t (in the absence of the Lemke Oliver-Soundararajan bias) … but the model in that 1974 paper tells a very different story, predicting a substantially stronger bias _against_ 6k sizes across ALL gap magnitudes, and for fairly large primes (not just the first million as the new authors use to demonstrate the bias in base 3). Given the incredible structure of these known harmonics, I was surprised to read the quotes from Granville and Ono in the Quanta article.
The new O(log log x / log x) term is fantastic, and I think the focused study on small modulo is warranted. But, I tend to agree with previous posters that the asymptotic behavior of consecutive primes was much better understood in the 20th century than most folks seem to realize. Personally, I have a hunch this bias has indeed been observed by many in the past, but was likely understood intuitively as a natural consequence of previously published phenomena.
21 March, 2016 at 8:52 am
Terence Tao
To be more precise: the prime tuples conjecture would (naively) predict, that all other things being equal, multiples of 3 would be twice as likely to be a prime difference than a non-multiple of 3 (though, as discussed in the post, there is a slight correction to this as pointed out by Lemke Oliver and Soundararajan). The situation with prime gaps is slightly different, because there is a bias against long gaps (more chance of having an intervening prime between the gap) that is not present in the case of differences, which is for instance why the entry for r=3 (corresponding to gaps of length 6) in Table 2 is significantly less than twice the entry for r=1 (corresponding to gaps of length 2). The inclusion-exclusion terms here give contributions of relative size , which are sizeable in the ranges considered in the Brent paper (in which
, which are sizeable in the ranges considered in the Brent paper (in which  ). But the main term in the absence of inclusion exclusion (in the notation of the paper, the k=1 term) still exhibits the behaviour I mentioned (for instance note that the r=3, k=1 term of Table 1 is exactly twice that of r=1, k=1).
). But the main term in the absence of inclusion exclusion (in the notation of the paper, the k=1 term) still exhibits the behaviour I mentioned (for instance note that the r=3, k=1 term of Table 1 is exactly twice that of r=1, k=1).
It is true though that the numerical evidence in ranges such as or
or  is not really dominated by the main term
is not really dominated by the main term  of the Lemke Oliver-Soundararajan bias, but is instead probably being driven more by the
of the Lemke Oliver-Soundararajan bias, but is instead probably being driven more by the  contributions. So it is perhaps somewhat serendipitous that the numerical evidence at this range still pointed in the direction of a bias, which caused the authors to investigate the situation theoretically and discern an asymptotic bias that was even stronger than what the numerical data suggested. (This is in contrast with some examples I listed in a previous comment (Mertens conjecture, second Hardy-Littlewood conjecture, and the story of Skewes’ number) in which the asymptotic
contributions. So it is perhaps somewhat serendipitous that the numerical evidence at this range still pointed in the direction of a bias, which caused the authors to investigate the situation theoretically and discern an asymptotic bias that was even stronger than what the numerical data suggested. (This is in contrast with some examples I listed in a previous comment (Mertens conjecture, second Hardy-Littlewood conjecture, and the story of Skewes’ number) in which the asymptotic 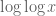 -type behaviour ran contrary to the small-scale numerical evidence).) It seems that numerical data can suggest a rough first approximation to the asymptotic truth, but one needs theory to get a more accurate picture once one is motivated by the initial numerics to study the situation more carefully (particularly when the strength of the effects involved are only logarithmic or double logarithmic in size).
-type behaviour ran contrary to the small-scale numerical evidence).) It seems that numerical data can suggest a rough first approximation to the asymptotic truth, but one needs theory to get a more accurate picture once one is motivated by the initial numerics to study the situation more carefully (particularly when the strength of the effects involved are only logarithmic or double logarithmic in size).
21 March, 2016 at 10:29 am
A. Mehta
Many thanks – this question has been bugging me for a week, and your explanation here makes things immensely more clear.
I should pay to have access to this kind of expert analysis!
21 March, 2016 at 9:28 am
Anonymous
As described in page 4 of the paper, the remainder term in conjecture 1.1 is expected to be given as a sum involving zeros of L-functions. Does it means that this remainder term is oscilatory, or perhaps it still has an inherent bias of the same size?
is expected to be given as a sum involving zeros of L-functions. Does it means that this remainder term is oscilatory, or perhaps it still has an inherent bias of the same size?
21 March, 2016 at 9:38 am
Terence Tao
From the same page of that paper, it seems that the authors do indeed expect such terms to be oscillatory, but that there are additional non-oscillatory terms (i.e. a further bias) of size about , and they hope to investigate this further in future work. So it seems there is going to be even more to this story than we know so far…
, and they hope to investigate this further in future work. So it seems there is going to be even more to this story than we know so far…
23 March, 2016 at 10:50 pm
Anonymous
In conjecture (1.1) it is clear that
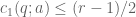
 are distinct
are distinct  .
.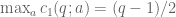 is attained for
is attained for  .
. to be unbounded!
to be unbounded!
with equality if and only if
Therefore
Showing the coefficient
This motivates the question: is it possible to extend conjecture 1.1 to the case where is an unbounded (sufficiently slowly) growing function of
is an unbounded (sufficiently slowly) growing function of  ? (allowing the bias to grow faster(!) then
? (allowing the bias to grow faster(!) then  ).
).
23 March, 2016 at 11:47 pm
Anonymous
Similarly,
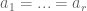 (mod
(mod  ).
).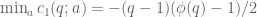
 and is also unbounded!
and is also unbounded!
with equality iff
Hence
is attained for
24 March, 2016 at 10:10 pm
Biases between consecutive primes
[…] https://terrytao.wordpress.com/2016/03/14/biases-between-consecutive-primes/ […]
26 March, 2016 at 8:02 am
jiangose
Reblogged this on jiangose.
26 March, 2016 at 8:21 am
Bias In The Primes | Gödel's Lost Letter and P=NP
[…] by Scientific American, by Nature, by the New Scientist, and by Quanta Magazine. Terry Tao also posted about it, and he explicates the gist in a wonderful […]
26 March, 2016 at 4:28 pm
My fun interaction with prime numbers this week | Mike's Math Page
[…] Terry Tao’s blog post about the new result […]
30 March, 2016 at 3:36 pm
Links for March 2016 - foreXiv
[…] the prime k-tuples conjecture, for which twin primes (cf. Yitang Zhang) are a special case. See Terrance Tao for detailed commentary. (H/t Peter […]
1 April, 2016 at 7:58 am
number theory news/ highlights: prime bias, Diffie-Hellman, Zhang-Tao, Wiles, Riemann | Turing Machine
[…] 5. Biases between consecutive primes | What’s new […]
3 April, 2016 at 8:04 pm
vznvzn
:!: :idea: :cool: :D <3 :star: these are groundbreaking and even near breakthrough results, and as not widely noted, empirical/ experimental approaches played a key role. think that much more may be possible from those who adopt a flexible attitude. recent new compilation, more on
empirical/ experimental CS/ math highlights
as a start on possible new empirical/ experimental attacks on the primes, what would a proof of the infinity of primes look like? some ideas on that in this post, hope to hear from others on it also
number theory news/ highlights: prime bias, Diffie-Hellman, Zhang-Tao, Wiles, Riemann
30 May, 2016 at 2:44 pm
BOUGRINE Lahoucine
Bonjour, Hello!
My question is : why mathematical scientists underestimate amateur researchers? Am asking such a question bescause it’s been more then two months that I am trying to publish a new method to find easily all primes but no one helped me. I have contacted mathematical scientists, scientific journals, and even some of my former teachers, no one believes me. I haven’t received answer yet. Could you please help me on that? Thank you in advance M.TAO
5 January, 2017 at 12:36 am
myzinsky
explain it to me i’m listening :)
5 February, 2017 at 3:34 am
Romain Viguier
we can consider the set of the 3 successive integers e1, e2, e3 as a reversible structure.
The metric is always of 1 but starting from both sides e1 and e3 (reversible), we do not have to manipulate time so it is ok.
So, starting from e1 and e3, we have a metric of 1. Thus, e2 will have the number 2 because metric starts from 0. But I think the number don’t exist, I would prefer to say that e2 has now a metric of 2 regarding e3-e1.
By multiplicating, we have an infinity of even number e2 (we generate all the even numbers according to the decimal system : 0,2,4,6,8).
There is a separation (extension) of 1 between e1 and e2 and between e2 and e3 (substraction and addition) : e1 and e3 will be uneven number like 1,3,5,7,9 (decimal system).
Euclide demonstrate the infinity of prime numbers.
Demonstration of twin prime numbers? No idea at all.
But maybe we have to take into account that we don’t generate new numbers but that we extend space metric in a discrete way. So it is a linear bubble that growth,and only 1 and the number itself respect the discrete metrics.
In informatics : a programming language can be low level or high level : I have really the impression of being very very low level : it is frustrating.
5 February, 2017 at 3:59 am
Romain Viguier
Actually, I realize I conflate distance and numbers. In my head, i get mixed up. Sorry.
21 November, 2017 at 12:22 pm
Teoria Universal (@TeoriaUniversal)
I regret to tell you that they are all wrong, the prime numbers have astonishing almost military distribution and
I regret to inform you that I already have the equation that everyone is looking for.
As you can imagine, I can say that: In the first 40,000 Natural Numbers there are 5,556 Prime Numbers, of which if the ordemanos in which digit ends, we can see the following.
Finished at 1 => 1.137
Finished at 3 => 1,147
Finished at 7 => 1.135
Finished at 9 => 1.135
plus 2 and 5 => 2
+ ————————
4.556.- NP in The first 40,000 Natural Numbers.
The Prime Numbers do not attract or repel each other, it only depends on the section analyzed and the average frequency in which the next one will appear.
As the principle is known, the frequency is smaller and for much larger numbers they move away.
THE solution is where nobody is looking for it.
“The trees do not let see the forest.”
I have an equation that I have called f (mx) that shows all NPs and applies to several behaviors.
If you dedicate yourself to finding answers, “There is always the possibility that you will find a result that will shake the world”.
There are the bases to develop a whole theory that will change many concepts, I share the idea that behind the NP are hidden many answers that govern the Universe.
Alvaro Unda
Cod.Post 1780000
10 May, 2018 at 3:50 am
Ignacio Villanueva
dear prof. Tao,
I have a question related to the Chebyshev bias: is there something known about how likely is it for number (not necessarily prime) p to be a quadratic residue mod q, with q prime? I am interested in the asymptotic behaviour as q grows to infinity.
best,
Ignacio
10 May, 2018 at 5:03 pm
Terence Tao
The quadratic residues mod q are a set of residues mod q, so the density of this set is
residues mod q, so the density of this set is  .
.
5 July, 2018 at 8:33 am
emini_guy
Another bias in the distribution of primes, that could have been discovered decades ago, was revealed recently: https://arxiv.org/abs/1807.00406
5 July, 2018 at 9:53 am
Anonymous
Perhaps this bias can also be explained by a relatively simple probabilistic argument.
6 July, 2018 at 3:41 am
Terence Tao
This seems likely. The prime tuples conjecture (generalised to linear forms) predicts, among other things, that the likelihood of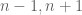 simultaneously being prime increases when
simultaneously being prime increases when  is divisible by small primes, and squarefree numbers are slightly less likely to be divisible by small primes than non-squarefree numbers.
is divisible by small primes, and squarefree numbers are slightly less likely to be divisible by small primes than non-squarefree numbers.
For instance, a general has a 40% chance of having one of
has a 40% chance of having one of 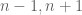 divisible by 5, whereas a multiple of 5 has no such possibility; thus, all other things being equal, one would expect a multiple of 5 to have a
divisible by 5, whereas a multiple of 5 has no such possibility; thus, all other things being equal, one would expect a multiple of 5 to have a 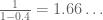 higher chance of being the midpoint of a twin prime pair than a random number (conversely, a non-multiple of 5 would be expected to have
higher chance of being the midpoint of a twin prime pair than a random number (conversely, a non-multiple of 5 would be expected to have  times the chance). Meanwhile, a typical number has a 1/5 chance of being divisible by 5, whereas a squarefree number has only a 4/24 chance of being divisible by 5 since the
times the chance). Meanwhile, a typical number has a 1/5 chance of being divisible by 5, whereas a squarefree number has only a 4/24 chance of being divisible by 5 since the 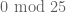 residue class is excluded. This effect alone would reduce the probability of a squarefree number being the midpoint of a prime pair by
residue class is excluded. This effect alone would reduce the probability of a squarefree number being the midpoint of a prime pair by  compared to that of a typical number, and this may already explain the bulk of the effect observed in this preprint.
compared to that of a typical number, and this may already explain the bulk of the effect observed in this preprint.
More generally, one can compare these sorts of numerically observed phenomena in the primes against the modified Cramer model. Here, what we are doing (combined with the restriction to multiples of 6 that is already in the preprint) is basically replacing “prime” by “integer not divisible by 2, 3, or 5” (the Cramer model requires us to actually take a random subset of this set, but for the purposes of computing ratios, the effect of further random sampling basically cancels itself out). It might be instructive to run the same numerical experiments in the preprint with such modified notions of prime (and attendant notions of twin prime, etc.) and see if one gets essentially the same statistics.
6 July, 2018 at 6:40 am
Anonymous
small typo: “0.86…” above should be “0.83…”
[Corrected, thanks – T.]
6 July, 2018 at 7:58 am
Anonymous
Thanks for the occasional elementary example:-) I see from your argument that the 1/36 probability reduction applies to numbers which aren’t squares of 5, but how do you know that it also applies to the subset of those numbers which are totally squarefree?
On 2nd thought there seem to be several independence assumptions in this argument, one of which (“all other things equal…”) is explicit. How do you know that they’re justified?
Typo: 0.86… -> 0.83…
7 July, 2018 at 1:38 pm
Terence Tao
A number is squarefree if and only if it is simultaneously not divisible by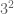 , by
, by 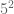 , by
, by  , etc.. Any fixed number of these conditions will be asymptotically independent, thanks to the Chinese remainder theorem. (More generally, it is a quite reliable heuristic that local conditions at different primes should behave independently of each other; cf. Section 3 of https://terrytao.wordpress.com/2015/01/04/254a-supplement-4-probabilistic-models-and-heuristics-for-the-primes-optional/ .) To deal with all of the congruence conditions at once requires some sieve theory (and perhaps also some quantitative control on the error term in the prime tuples conjecture), however one would expect that this would be relatively straightforward since
, etc.. Any fixed number of these conditions will be asymptotically independent, thanks to the Chinese remainder theorem. (More generally, it is a quite reliable heuristic that local conditions at different primes should behave independently of each other; cf. Section 3 of https://terrytao.wordpress.com/2015/01/04/254a-supplement-4-probabilistic-models-and-heuristics-for-the-primes-optional/ .) To deal with all of the congruence conditions at once requires some sieve theory (and perhaps also some quantitative control on the error term in the prime tuples conjecture), however one would expect that this would be relatively straightforward since  and so this is almost a finite sieve (the effect of small primes dominate that of large primes).
and so this is almost a finite sieve (the effect of small primes dominate that of large primes).
9 March, 2021 at 10:21 am
ES
I was wondering what happens with the bias if one considers things like $\sum_{n\leq H} f_3(n) f_3(n+1)$. Do you think the bias will persist? In this case it would give $c_1^2 H-2 c_1 c_2 \log H+O(1)$ but the secondary term could turn out to be of order $\log^2 H$ instead.
27 September, 2022 at 10:24 pm
Florian Neubauer
If we use the Sieve of Eratosthenes and stop sieving after 3, all of the remaining consecutive prime candidates fall in alternating residue classes (mod 3). If we stop sieving after 5, there are still 3 consecutive prime candidates falling in alternating classes for 2 successors that fall in the same class as their precursors. Can’t we simply use the argument that multiples of 5 have the highest frequency of all multiples of primes >3, and hence the multiples of primes larger 5 will never be able to remove this bias towards alternating residue classes entirely?
18 August, 2023 at 8:50 pm
https://www.researchgate.net/publication/232697474_Highly_biased_prime_number_ra - Homework Plug
[…] Biases between consecutive primes […]