254A, Supplement 4: Probabilistic models and heuristics for the primes (optional)

4 January, 2015 in 254A - analytic prime number theory, math.NT, math.PR | Tags: Cramer's random model, GUE hypothesis, Mobius function, model, prime numbers, pseudorandomness | by Terence Tao

We now move away from the world of multiplicative prime number theory covered in Notes 1 and Notes 2, and enter the wider, and complementary, world of non-multiplicative prime number theory, in which one studies statistics related to non-multiplicative patterns, such as twins ${n,n+2}$ . This creates a major jump in difficulty; for instance, even the most basic multiplicative result about the primes, namely Euclid’s theorem that there are infinitely many of them, remains unproven for twin primes. Of course, the situation is even worse for stronger results, such as Euler’s theorem, Dirichlet’s theorem, or the prime number theorem. Finally, even many multiplicative questions about the primes remain open. The most famous of these is the Riemann hypothesis, which gives the asymptotic ${\sum_{n \leq x} \Lambda(n) = x + O( \sqrt{x} \log^2 x )}$ (see Proposition 24 from Notes 2). But even if one assumes the Riemann hypothesis, the precise distribution of the error term ${O( \sqrt{x} \log^2 x )}$ in the above asymptotic (or in related asymptotics, such as for the sum ${\sum_{x \leq n < x+y} \Lambda(n)}$ that measures the distribution of primes in short intervals) is not entirely clear.

Despite this, we do have a number of extremely convincing and well supported models for the primes (and related objects) that let us predict what the answer to many prime number theory questions (both multiplicative and non-multiplicative) should be, particularly in asymptotic regimes where one can work with aggregate statistics about the primes, rather than with a small number of individual primes. These models are based on taking some statistical distribution related to the primes (e.g. the primality properties of a randomly selected ${k}$ -tuple), and replacing that distribution by a model distribution that is easy to compute with (e.g. a distribution with strong joint independence properties). One can then predict the asymptotic value of various (normalised) statistics about the primes by replacing the relevant statistical distributions of the primes with their simplified models. In this non-rigorous setting, many difficult conjectures on the primes reduce to relatively simple calculations; for instance, all four of the (still unsolved) Landau problems may now be justified in the affirmative by one or more of these models. Indeed, the models are so effective at this task that analytic number theory is in the curious position of being able to confidently predict the answer to a large proportion of the open problems in the subject, whilst not possessing a clear way forward to rigorously confirm these answers!

As it turns out, the models for primes that have turned out to be the most accurate in practice are random models, which involve (either explicitly or implicitly) one or more random variables. This is despite the prime numbers being obviously deterministic in nature; no coins are flipped or dice rolled to create the set of primes. The point is that while the primes have a lot of obvious multiplicative structure (for instance, the product of two primes is never another prime), they do not appear to exhibit much discernible non-multiplicative structure asymptotically, in the sense that they rarely exhibit statistical anomalies in the asymptotic limit that cannot be easily explained in terms of the multiplicative properties of the primes. As such, when considering non-multiplicative statistics of the primes, the primes appear to behave pseudorandomly, and can thus be modeled with reasonable accuracy by a random model. And even for multiplicative problems, which are in principle controlled by the zeroes of the Riemann zeta function, one can obtain good predictions by positing various pseudorandomness properties of these zeroes, so that the distribution of these zeroes can be modeled by a random model.

Of course, one cannot expect perfect accuracy when replicating a deterministic set such as the primes by a probabilistic model of that set, and each of the heuristic models we discuss below have some limitations to the range of statistics about the primes that they can expect to track with reasonable accuracy. For instance, many of the models about the primes do not fully take into account the multiplicative structure of primes, such as the connection with a zeta function with a meromorphic continuation to the entire complex plane; at the opposite extreme, we have the GUE hypothesis which appears to accurately model the zeta function, but does not capture such basic properties of the primes as the fact that the primes are all natural numbers. Nevertheless, each of the models described below, when deployed within their sphere of reasonable application, has (possibly after some fine-tuning) given predictions that are in remarkable agreement with numerical computation and with known rigorous theoretical results, as well as with other models in overlapping spheres of application; they are also broadly compatible with the general heuristic (discussed in this previous post) that in the absence of any exploitable structure, asymptotic statistics should default to the most “uniform”, “pseudorandom”, or “independent” distribution allowable.

As hinted at above, we do not have a single unified model for the prime numbers (other than the primes themselves, of course), but instead have an overlapping family of useful models that each appear to accurately describe some, but not all, aspects of the prime numbers. In this set of notes, we will discuss four such models:

The Cramér random model and its refinements, which model the set ${{\mathcal P}}$ of prime numbers by a random set.
The Möbius pseudorandomness principle, which predicts that the Möbius function ${\mu}$ does not correlate with any genuinely different arithmetic sequence of reasonable “complexity”.
The equidistribution of residues principle, which predicts that the residue classes of a large number ${n}$ modulo a small or medium-sized prime ${p}$ behave as if they are independently and uniformly distributed as ${p}$ varies.
The GUE hypothesis, which asserts that the zeroes of the Riemann zeta function are distributed (at microscopic and mesoscopic scales) like the zeroes of a GUE random matrix, and which generalises the pair correlation conjecture regarding pairs of such zeroes.

This is not an exhaustive list of models for the primes and related objects; for instance, there is also the model in which the major arc contribution in the Hardy-Littlewood circle method is predicted to always dominate, and with regards to various finite groups of number-theoretic importance, such as the class groups discussed in Supplement 1, there are also heuristics of Cohen-Lenstra type. Historically, the first heuristic discussion of the primes along these lines was by Sylvester, who worked informally with a model somewhat related to the equidistribution of residues principle. However, we will not discuss any of these models here.

A word of warning: the discussion of the above four models will inevitably be largely informal, and “fuzzy” in nature. While one can certainly make precise formalisations of at least some aspects of these models, one should not be inflexibly wedded to a specific such formalisation as being “the” correct way to pin down the model rigorously. (To quote the statistician George Box: “all models are wrong, but some are useful”.) Indeed, we will see some examples below the fold in which some finer structure in the prime numbers leads to a correction term being added to a “naive” implementation of one of the above models to make it more accurate, and it is perfectly conceivable that some further such fine-tuning will be applied to one or more of these models in the future. These sorts of mathematical models are in some ways closer in nature to the scientific theories used to model the physical world, than they are to the axiomatic theories one is accustomed to in rigorous mathematics, and one should approach the discussion below accordingly. In particular, and in contrast to the other notes in this course, the material here is not directly used for proving further theorems, which is why we have marked it as “optional” material. Nevertheless, the heuristics and models here are still used indirectly for such purposes, for instance by

giving a clearer indication of what results one expects to be true, thus guiding one to fruitful conjectures;
providing a quick way to scan for possible errors in a mathematical claim (e.g. by finding that the main term is off from what a model predicts, or an error term is too small);
gauging the relative strength of various assertions (e.g. classifying some results as “unsurprising”, others as “potential breakthroughs” or “powerful new estimates”, others as “unexpected new phenomena”, and yet others as “way too good to be true”); or
setting up heuristic barriers (such as the parity barrier) that one has to resolve before resolving certain key problems (e.g. the twin prime conjecture).

See also my previous essay on the distinction between “rigorous” and “post-rigorous” mathematics, or Thurston’s essay discussing, among other things, the “definition-theorem-proof” model of mathematics and its limitations.

Remark 1 The material in this set of notes presumes some prior exposure to probability theory. See for instance this previous post for a quick review of the relevant concepts.

— 1. The Cramér random model —

We begin by introducing the “naive” Cramér random model for the primes ${{\mathcal P}}$ , explicitly introduced by Harald Cramér in 1936. The naive version of the Cramér model is a little too oversimplified to give very accurate results, but tends to give predictions of the right order of magnitude at least, and will serve as a basis for a more accurate version of the Cramér model to be introduced shortly.

The starting point for the model is the prime number theorem, which implies that there are approximately ${\frac{\varepsilon x}{\log x}}$ primes between ${x}$ and ${x+\varepsilon x}$ for any fixed ${\varepsilon > 0}$ and large ${x}$ . Thus, if one chooses a natural number ${n}$ at random in ${[x, x+\varepsilon x]}$ , the probability that it will be prime is about ${\frac{1}{\log x} \approx \frac{1}{\log n}}$ . Inspired by this, we construct a random model ${{\mathcal P}'}$ of the primes ${{\mathcal P}}$ to be a random subset of the natural numbers, such that each natural number ${n > 2}$ has an independent probability of ${\frac{1}{\log n}}$ of lying in ${{\mathcal P}'}$ , thus

$\displaystyle \mathop{\bf P}( n_1, \dots, n_k \in {\mathcal P'} ) = \frac{1}{\log n_1 \dots \log n_k} \ \ \ \ \ (1)$

for all distinct ${n_1,\dots,n_k > 2}$ . We exclude ${2}$ from consideration in (1) to avoid the issue that ${\frac{1}{\log 2}}$ is greater than one, and thus cannot serve as a probability. The membership of ${1}$ and ${2}$ in ${{\mathcal P}'}$ is not of any great importance, but given that ${{\mathcal P}'}$ is supposed to model ${{\mathcal P}}$ , let us require that ${1 \not \in {\mathcal P}'}$ and ${2 \in {\mathcal P}'}$ . We ignore here the (routine) measure-theoretic machinery needed to rigorously construct a probability space that can support a countably infinite number of random variables, as this set of notes is not focused on rigorous formalism. (See for instance this previous post for the relevant theory needed.)

We then have

Model 2 (Naive Cramér random model) The asymptotic statistics for the set of primes ${{\mathcal P}}$ should (almost surely) behave like the asymptotic statistics of the random set ${{\mathcal P}'}$ .

This model asserts that while the set ${{\mathcal P}}$ of primes is certainly deterministic, it is pseudorandom, in the sense that it behaves like a random set, namely ${{\mathcal P}'}$ . The naive version of the Cramér model uses a random set ${{\mathcal P}'}$ that has no structure beyond its density.

Let’s see some basic predictions of this model. The first is that it recovers the Riemann hypothesis (cf. Proposition 24 of Notes 2):

Prediction 3 (Riemann hypothesis) For any fixed ${\varepsilon>0}$ , we have

$\displaystyle \sum_{n \leq x} \Lambda(n) = x + O_\varepsilon( x^{1/2+\varepsilon}) \ \ \ \ \ (2)$

for ${x > 1}$ .

Proof: (Uses naive Cramér model) The contribution of those ${n}$ that are squares or higher order of primes can be easily seen to be ${O( x^{1/2+\varepsilon})}$ , so it suffices to show that

$\displaystyle \sum_{n \leq x} 1_{\mathcal P}(n) \log n = x + O_\varepsilon( x^{1/2+\varepsilon}).$

We then invoke the Cramér random model, and verify that almost surely one has

$\displaystyle \sum_{n \leq x} 1_{{\mathcal P}'}(n) \log n = x + O_\varepsilon( x^{1/2+\varepsilon}).$

for all ${x}$ (here we allow the implied constant in the ${O_\varepsilon()}$ notation to be random). By the Borel-Cantelli lemma, it suffices for each fixed choice of ${x}$ (which we can take to be a natural number) to obtain the estimate

$\displaystyle \sum_{n \leq x} 1_{{\mathcal P}'}(n) \log n = x + O_\varepsilon( x^{1/2+\varepsilon}) \ \ \ \ \ (3)$

with probability ${1-O(x^{-2})}$ (say).

Fix ${x}$ , and consider the random variable

$\displaystyle X := \sum_{n \leq x} 1_{{\mathcal P}'}(n) \log n$

which we rewrite as

$\displaystyle X = x + O(1) + \sum_{2 < n \leq x} X_n$

where

$\displaystyle X_n := 1_{{\mathcal P}'}(n) \log n - 1.$

From (1), the ${X_n}$ have mean zero and are independent, and have size ${O( \log x ) = O( x^{o(1)} )}$ . Thus

$\displaystyle \mathop{\bf E} (\sum_{2 < n \leq x} X_n)^k = O_k( x^{k/2+o(1)})$

for any fixed natural number ${k}$ (the only terms in ${(\sum_{2 < n \leq x} X_n)^k}$ that give a non-zero contribution are those in which each ${X_n}$ appears at least twice, so there are at most ${k/2}$ distinct indices of ${n}$ that arise, and so there are only ${O_k(x^{k/2})}$ such terms, each contributing ${O(x^{o(1)})}$ . From Chebyshev’s inequality this implies that ${\sum_{n \leq x} X_n = O( x^{1/2+\varepsilon})}$ with probability ${1-O( x^{-k\varepsilon + o(1)})}$ . Setting ${k}$ sufficiently large depending on ${\varepsilon}$ , we obtain the claim. $\Box$

Remark 4 One could also have proven the above claim using concentration of measure results such as the Chernoff inequality, as discussed in this previous blog post. The estimate (2) reflects the general heuristic of expected square root cancellation: when summing ${O(x)}$ “independent” expressions, each of size ${O(A)}$ , the sum should typically deviate by ${O_\varepsilon( x^{1/2+\varepsilon} A)}$ around its expected value, thus saving a factor of about ${\sqrt{x}}$ over the trivial deviation bound of ${O(xA)}$ .

Exercise 5 Use the naive Cramér model to predict the size of the error term iCn the first, second, and third Mertens theorems (Theorems 33, 36, 42 from Notes 1). (Note that the Cramér model will not predict the constant ${e^\gamma}$ in the third Mertens theorem, as this constant is sensitive to the values of small primes, which the Cramér model does not accurately model; however, the model can predict a rate of convergence with ${e^\gamma}$ replaced by an unspecified constant, which can then a posteriori be matched with ${e^\gamma}$ using the existing version of the third Mertens theorem.)

Remark 6 The fact that the naive Cramér model recovers essentially the same prediction on the prime number error term as the Riemann hypothesis (up to factors of ${x^\varepsilon}$ ) is encouraging as far as evidence for the Riemann hypothesis is concerned. But one should caution that due to the multiplicative structure of the von Mangoldt function (as evidenced by the explicit formula), the naive Cramér model does not quite give the right bounds on error terms if one looks at the ${x^\varepsilon}$ factors more carefully. For instance, from the smoothed explicit formula (Exercise 22 of Notes 2) it is a routine matter (using Proposition 16 from Notes 2 and Exercise 28 of Supplement 2) to arrive at the bound

$\displaystyle \sum_n \Lambda(n) g(\log n - \log x) = x \hat g(-i) + O_g( x^{1/2} )$

assuming the Riemann hypothesis for a fixed smooth, compactly supported function ${g: {\bf R} \rightarrow {\bf C}}$ and all ${x > 1}$ . On the other hand, if one applies the naive Cramér random model, the quantity ${\sum_n \Lambda(n) g(\log n - \log x) - x \hat g(-i)}$ becomes modeled by a quantity of mean ${O_g(x^{1/2})}$ and variance comparable to ${x \log x}$ ; we leave this computation as an exercise to the interested reader. This suggests that the error term should be closer to ${x^{1/2} \log^{1/2} x}$ than to ${x^{1/2}}$ . Thus we see that the explicit formula, which is a feature of the genuine primes that are not present in the Cramér random model, bestows (on the Riemann hypothesis) slightly subrandom behaviour on the primes – the error terms can in fact be slightly better than what a purely random model predicts! (See Section 4 below for further examples of this subrandom behaviour.) Ultimately, the reason for this is that the multiplicative semigroup ${\langle {\mathcal P} \rangle}$ generated by the primes – that is to say, the natural numbers ${{\bf N}}$ – is unusually well distributed in the sense that ${\sum_{n \in \langle {\mathcal P} \rangle: n \leq x} 1 = x + O(1)}$ , which we have seen in previous notes to lead to an meromorphic continuation of the zeta function to the left of the critical line. In contrast, almost any conceivable Cramér-type random model ${{\mathcal P}'}$ for the primes will only have a distribution of ${\sum_{n \in \langle {\mathcal P} \rangle: n \leq x} 1 = x + O_\varepsilon(x^{1/2+\varepsilon})}$ at best (where we view ${\langle {\mathcal P} \rangle}$ as a multiset, so the sum is weighted by multiplicity), and so cannot capture consequences of this subrandom distribution of ${\langle {\mathcal P} \rangle}$ , such as the explicit formula. However, it appears that such deviations from random behaviour are only significant if one wishes to obtain accuracy better than ${O( x^{1/2+\varepsilon})}$ in one’s estimates, and so one should not be too concerned about such deviations if one is willing to concede these ${O( x^{1/2+\varepsilon})}$ errors. See this paper of Pintz for further discussion of this deviation of the primes from Cramér type models.

Next, we give another prediction of the naive Cramér model, which was in fact Cramér’s original motivation for introducing the model. For any ${X > 3}$ , let

$\displaystyle G(X) := \sup_{n: p_n, p_{n+1} \leq X} p_{n+1} - p_n$

denote the largest gap between the primes up to ${X}$ , where ${p_n}$ denotes the ${n^{th}}$ prime.

Conjecture 7 (Cramér conjecture) One has ${G(X) = (1+o(1)) \log^2 X}$ as ${X \rightarrow \infty}$ .

Note that this conjecture would imply Legendre’s conjecture that there is always a prime between ${n^2}$ and ${(n+1)^2}$ , at least for sufficiently large ${n}$ ; indeed, any bound of the shape ${G(X) = o(X^{1/2})}$ would suffice for this purpose. Intuitively, the reason for this is that with an average density of ${\log X}$ , the probability that a given gap between primes exceeds ${A \log X}$ should be like ${e^{-A}}$ ; as one has ${X^{1+o(1)}}$ gaps to play with, the largest gap that one still expects to actually occur would then be of size ${A \log X}$ with ${e^{-A} \approx 1/X^{1+o(1)}}$ , which explains the ${\log^2 X}$ factor.

Proof: (Uses naive Cramér model) Let ${p'_1, p'_2, \dots}$ be the elements of the random set ${{\mathcal P}'}$ in increasing order, and let ${G'(X)}$ be the random variable

$\displaystyle G'(X) := \sup_{n: p'_n, p'_{n+1} \leq X} p'_{n+1} - p'_n$

Invoking the naive Cramér model, we will verify that almost surely one has

$\displaystyle G'(X) = (1+o(1)) \log^2 X$

as ${X \rightarrow \infty}$ . By the Borel-Cantelli lemma (and restricting ${X}$ to be a power of two), it suffices to show for each ${0 < \varepsilon < 1/2}$ and ${X>2}$ that one has

$\displaystyle G'(X) \leq (1+\varepsilon) \log^2 X \ \ \ \ \ (4)$

and

$\displaystyle G'(X) \geq (1-\varepsilon) \log^2 X \ \ \ \ \ (5)$

with probability ${1 - O_\varepsilon(X^{-\varepsilon})}$ (say).

We begin with (4). To show this bound, it suffices to show that every discrete interval in ${[3,X]}$ of cardinality ${L_+ := \lfloor (1+\varepsilon) \log^2 X \rfloor-1}$ contains at least one element of ${{\mathcal P}'}$ . There are ${O(X)}$ such intervals, so by the union bound it suffices to show that for any given interval ${I}$ , the probability that ${I}$ contains at least one element of ${{\mathcal P}'}$ is at least ${1 - O_\varepsilon(X^{-3})}$ . From (1) and the inclusion-exclusion principle, this probability is precisely

$\displaystyle 1 - \prod_{n \in I} (1 - \frac{1}{\log n}).$

Upper bounding ${1 - \frac{1}{\log n}}$ by ${\exp( -\frac{1}{\log X} )}$ , this probability is at least ${1 - \exp( -L_+ / \log X )}$ , and the claim follows.

Now we show (5). Observe that the interval ${[X/4,X/2]}$ contains ${\gg X / \log^2 X}$ disjoint discrete intervals ${I_1,\dots,I_m}$ of cardinality ${L_- := \lceil (1-\varepsilon) \log^2 X \rceil}$ . It will suffice to show that with probability ${1 - O_\varepsilon(X^{-2})}$ , at least one of these intervals is disjoint from ${{\mathcal P}'}$ . (It is easy to see that the interval ${(X/2,X]}$ will contain at least one element of ${{\mathcal P}'}$ with probability ${1 - O_\varepsilon( X^{-2} )}$ .) By (1), the probability that a given interval ${I_j}$ has this property is

$\displaystyle \prod_{n \in I} (1 - \frac{1}{\log n}).$

Lower bounding ${1 - \frac{1}{\log n}}$ by ${\exp( -\frac{1-o(1)}{\log X})}$ , where the ${o(1)}$ goes to zero as ${X \rightarrow \infty}$ keeping ${\varepsilon}$ fixed, we see that the probability that a given ${I_j}$ is disjoint from ${{\mathcal P}'}$ is at least

$\displaystyle \exp( - (1-o(1)) L_- / \log X ) = X^{-1+\varepsilon + o(1)}.$

As the events that ${I_j}$ are disjoint from ${{\mathcal P}'}$ are independent in ${j}$ , the probability that none of them are disjoint from ${{\mathcal P}'}$ is then at most

$\displaystyle (1 - X^{-1+\varepsilon + o(1)})^m = 1 - O( \exp( - X^{\varepsilon+o(1)} ) )$

and the claim follows. $\Box$

As it turns out, we now believe this prediction of the naive Cramér model to be slightly incorrect; see below. For the most recent rigorous lower bounds on ${G(X)}$ , see this recent post. As for upper bounds, it was shown by Cramér on the Riemann hypothesis that ${G(X) \ll X^{1/2} \log X}$ , and a slight further improvement under the additional assumption of the pair correlation conjecture (see Section 4 below) was obtained by Heath-Brown.

Our final example of the naive Cramér model is to the twin prime conjecture.

Prediction 8 (Twin prime asymptotic, first attempt) We have

$\displaystyle \# \{ p \leq x: p, p+2 \in {\mathcal P}\} = (1+o(1)) \frac{x}{\log^2 x}$

as ${x \rightarrow \infty}$ . In particular, there are infinitely many primes ${p}$ such that ${p+2}$ is also prime.

Intuitively, the reason for this asymptotic is that for most of the ${O(x)}$ numbers ${n}$ between ${3}$ and ${x}$ , each of ${n}$ and ${n+2}$ have an independent probability of about ${1/\log x}$ being prime (or more precisely, of lying in the Cramér model for the primes), so the probability that they are both prime should be about ${1/\log^2 x}$ .

Proof: (Uses naive Cramér model) We will show that

$\displaystyle \# \{ p \leq x: p, p+2 \in {\mathcal P}'\} = (1+o(1)) \frac{x}{\log^2 x} \ \ \ \ \ (6)$

almost surely. By the Borel-Cantelli lemma again, it suffices to show that for each ${x > 2}$ , we have (6) with probability ${1 - O(x^{-2+o(1)})}$ (say) as ${x \rightarrow \infty}$ .

Fix ${x}$ . We write the left-hand side as

$\displaystyle O(1) + \sum_{2 \leq n \leq x} \frac{1}{(\log n) \log(n+2)} + X_n$

where

$\displaystyle X_n := 1_{{\mathcal P}'}(n) 1_{{\mathcal P}'}(n+2) - \frac{1}{(\log n) \log(n+2)}.$

To estimate the sum ${\sum_{2 \leq n \leq x} \frac{1}{(\log n) \log(n+2)}}$ , we can easily check that the contribution with ${n \leq x / \log^3 x}$ is ${o(x/\log^2 x)}$ , and for the remaining portion we have ${\frac{1}{(\log n) \log(n+2)} = \frac{1+o(1)}{\log^2 x}}$ , and thus

$\displaystyle \sum_{2 \leq n \leq x} \frac{1}{(\log n) \log(n+2)} = (1+o(1)) \frac{x}{\log^2 x}.$

It thus suffices to show that

$\displaystyle \sum_{2 \leq n \leq x} X_n = o( \frac{x}{\log^2 x} )$

with probability ${1 - O(x^{-2+o(1)})}$ . But from (1), each ${X_n}$ has mean zero, is bounded by ${O(1)}$ , and ${X_n}$ is independent of ${X_m}$ unless ${|n-m| \leq 2}$ , from which we easily calculate that

$\displaystyle \mathop{\bf E} (\sum_{2 \leq n \leq x} X_n)^2 = O(x).$

A direct application of Chebyshev’s inequality then gives the required bound with a failure probability of ${O( x^{-1+o(1)})}$ , which is not quite good enough for our purposes; but a similar calculation gives

$\displaystyle \mathop{\bf E} (\sum_{2 \leq n \leq x} X_n)^4 = O(x^2),$

which is sufficient. (Alternatively, one can first round ${x}$ to the nearest power of ${1+\varepsilon}$ for a small fixed ${\varepsilon>0}$ , in which case Borel-Cantelli would already work with a failure probability as large as, say, ${O(\log^{-2} x)}$ .) $\Box$

Exercise 9 Sharpen the prediction of the naive Cramér model to

$\displaystyle \# \{ p \leq x: p, p+2 \in {\mathcal P}\} = \int_2^x \frac{dt}{(\log t) \log(2+t)} + O_\varepsilon( x^{1/2+\varepsilon} )$

for any ${\varepsilon>0}$ and ${x > 2}$ .

Unfortunately, the above argument reveals a significant drawback to the naive Cramér model, in that the same argument also predicts the asymptotic

$\displaystyle \# \{ p \leq x: p, p+1 \in {\mathcal P}\} = (1+o(1)) \frac{x}{\log^2 x},$

implying that there are an infinite number of consecutive primes ${p,p+1}$ . This is of course absurd, since all but one of the primes ${p \in {\mathcal P}}$ are odd. The problem is that the naive Cramér model does not take into account the severe irregularity in the distribution of the primes ${{\mathcal P}}$ with respect to the residue classes modulo ${2}$ . One also needs to take into account irregularity modulo ${3}$ , to avoid predicting the infinitude of prime triplets ${p,p+2,p+4}$ (note that as one of ${p,p+2,p+4}$ must be divisible by ${3}$ , the only prime triplet is in fact ${3,5,7}$ ); and so forth. We formalise this with the following revision of the Cramér model. Given a parameter ${w \geq 2}$ , let ${W:= \prod_{p \leq w} p}$ denote the product of all the primes up to ${w}$ (this is sometimes known as the primorial of ${w}$ ). Note that after removing the primes less than or equal to ${w}$ , all the remaining primes lie in the ${\phi(W)}$ residue classes ${b\ (W)}$ with ${b}$ coprime to ${W}$ . From the prime number theorem in arithmetic progressions (Exercise 50 from Notes 2), we expect (for ${x}$ sufficiently large depending on ${w}$ ) each such residue class to contain about ${\frac{x}{\phi(W) \log x}}$ primes less than or equal to ${x}$ , compared to about ${\frac{x}{W}}$ natural numbers less than or equal to ${x}$ , leading to a density of ${\frac{W}{\phi(W) \log x}}$ . This motivates a variant ${{\mathcal P}'_w}$ of the random set ${{\mathcal P}'}$ , defined by letting ${{\mathcal P}'_w}$ consist (deterministically) of the primes up to ${w}$ , together with a random subset of those natural numbers coprime to ${W}$ , with

$\displaystyle \mathop{\bf P}( n_1, \dots, n_k \in {\mathcal P'}_w ) = \prod_{i=1}^k \min( \frac{W}{\phi(W) \log n_i}, 1)$

for distinct ${n_1,\dots,n_k}$ coprime to ${W}$ . (The minimum here is to ensure that probabilities stay less than ${1}$ , and can be largely ignored in practice.) Thus, for instance, ${{\mathcal P}'_2}$ consists of the prime ${2}$ together with a random set of odd numbers, with each large odd number ${n}$ having an independent probability of ${\frac{2}{\log n}}$ of lying in ${{\mathcal P}'_2}$ . Similarly, ${{\mathcal P}'_3}$ consists of the primes ${2}$ and ${3}$ , together with a random set of numbers coprime to ${6}$ , with each such large number ${n}$ having an independent probability of ${\frac{3}{\log n}}$ of lying in ${{\mathcal P}'_3}$ . We then have the following (somewhat imprecise) modification of the Cramér model:

Model 10 (Modified Cramér random model) The asymptotic statistics for the set of primes ${{\mathcal P}}$ up to some threshold ${x}$ should (almost surely) behave like the asymptotic statistics of the random set ${{\mathcal P}'_w}$ for ${w}$ slowly growing in ${x}$ (or alternatively as the limit of the statistics of ${{\mathcal P}'_w}$ for fixed ${w}$ , in the limit ${w \rightarrow \infty}$ ).

This model is not as precise as the naive Cramér model, because it does not specify exactly how ${w}$ is to depend on ${x}$ , but in many applications it does not matter so much (except perhaps for predicting the size of error terms) exactly what ${w}$ is, so long as it grows slowly (e.g. ${\log x}$ or slower).

We illustrate this model with an refined prediction for the twin prime conjecture.

Prediction 11 (Refined twin prime asymptotic) We have

$\displaystyle \# \{ p \leq x: p, p+2 \in {\mathcal P}\} = (2\Pi_2+o(1)) \frac{x}{\log^2 x}$

as ${x \rightarrow \infty}$ , where ${\Pi_2}$ is the twin primes constant, defined as

$\displaystyle \Pi_2 := \prod_{p \in {\mathcal P}: p >2} (1 - \frac{1}{(p-1)^2}) = 0.6601618\dots. \ \ \ \ \ (7)$

In particular, there are infinitely many primes ${p}$ such that ${p+2}$ is also prime.

In analogy with Exercise 9, one is led to the refined prediction

$\displaystyle \# \{ p \leq x: p, p+2 \in {\mathcal P}\}$

$\displaystyle = 2\Pi_2 \int_2^x \frac{dt}{(\log t)\log(t+2)} + O_\varepsilon(x^{1/2+\varepsilon})$

for any fixed ${\varepsilon}$ . This prediction matches well with numerics. For instance, the number of twin primes up to ${10^{10}}$ is ${27,412,679}$ , which is within ${0.004\%}$ of the prediction given by the above formula (in contrast, (8) is off by about thirty percent). (See this web page of Gourdon and Sebah for some further numerical statistics on twin primes.)

Proof: (Uses modified Cramér model; informal) The argument here is essentially due to Pólya. We study the statistic

$\displaystyle \# \{ p \leq x: p, p+2 \in {\mathcal P}_w\} \ \ \ \ \ (8)$

for fixed ${w}$ and large ${x}$ . The primes less than or equal to ${w}$ contribute ${O_w(1)}$ to this statistic, so we restrict attention to those ${p}$ with ${p > w}$ . A residue class ${b\ (W)}$ only contributes to the above statistic in case ${b}$ and ${b+2}$ are both coprime to ${W}$ ; by the Chinese remainder theorem, the number of such residue classes is

$\displaystyle \prod_{2 < p \leq w} (p-2).$

On the other hand, a modification of the computation in Prediction 8 shows that the contribution of a given residue class ${b\ (W)}$ with ${b,b+2}$ both coprime to ${W}$ should be

$\displaystyle (1+o(1)) \frac{x}{W} \times (\frac{W}{\phi(W) \log x})^2$

with “high probability” (we do not quantify this term here). Thus the total size of (8) should be approximately

$\displaystyle (1+o(1)) \frac{x}{W} \times (\frac{W}{\phi(W) \log x})^2 \times \prod_{2 < p \leq w} (p-2) + O_w(1).$

This simplifies as

$\displaystyle (2 \prod_{2 < p \leq w} (1 - \frac{1}{(p-1)^2}) + o(1)) \frac{x}{\log^2 x}.$

Letting ${w}$ grow slowly to infinity, we obtain the claim. $\Box$

Note now that we do not run into the problem of the Cramér model predicting infinitely many pairs of consecutive primes (as ${{\mathcal P}'_w}$ will avoid such patterns once ${w \geq 2}$ ), or infinitely many prime triplets ${p,p+2,p+4}$ , etc.

The modified Cramér model already predicts answers (and asymptotics) to many of the basic unsolved questions in analytic prime number theory, including an affirmative answer to all four of Landau’s problems; these are discussed in the exercises below.

Exercise 12 (Goldbach conjecture) Let ${N}$ be a large even number. Use the modified Cramér model to predict that the number of ways to represent ${N}$ as the sum ${N=p+q}$ of two primes is equal to

$\displaystyle (2 \Pi_2 (\prod_{p > 2: p|N} \frac{p-1}{p-2}) + o(1)) \frac{N}{\log^2 N} \ \ \ \ \ (9)$

as ${N \rightarrow \infty}$ . In particular, the even Goldbach conjecture should be true for sufficiently large even numbers. Given that this conjecture has been numerically verified for even integers up to about ${10^{18}}$ , it is thus widely expected that this conjecture is true.

Exercise 13 (Hardy-Littlewood prime tuples conjecture) Let ${k \geq 1}$ , and let ${(h_1,\dots,h_k)}$ be a tuple of distinct integers which are admissible in the sense that for every prime ${p}$ , there is at least one residue class ${a_p\ (p)}$ that is disjoint from all of the ${h_1,\dots,h_k}$ . (For instance, ${(0,2,6)}$ is admissible, but ${(0,1)}$ or ${(0,2,4)}$ is not admissible.) Use the modified Cramér model to predict the Hardy-Littlewood prime tuples conjecture:

$\displaystyle \#\{ n \leq x: n+h_1,\dots,n+h_k \in {\mathcal P}\} = ({\mathfrak S} + o(1)) \frac{x}{\log^k x} \ \ \ \ \ (10)$

as ${x \rightarrow \infty}$ , where ${{\mathfrak S}}$ is the singular series

$\displaystyle {\mathfrak S} := \prod_p \frac{1 - \omega(p) / p}{(1-1/p)^k}$

and ${\omega(p)}$ is the number of distinct residue classes that the ${h_1,\dots,h_k}$ lie in modulo ${p}$ . Show also that ${{\mathfrak S}}$ is convergent to a non-zero number when the tuple ${(h_1,\dots,h_k)}$ is admissible; in particular, the modified Cramér model predicts that there are infinitely many ${n}$ such that ${n+h_1,\dots,n+h_k}$ are simultaneously prime.

Again in analogy with Exercise 9, one expects to be able to improve (10) to

$\displaystyle \sum_{n \leq x} \Lambda(n+h_1) \dots \Lambda(n+h_k) = {\mathfrak S} x + O_{k,\varepsilon}( x^{1/2+\varepsilon} ) \ \ \ \ \ (11)$

for any ${\varepsilon>0}$ and ${h_1,\dots,h_k = O( x^{1-\varepsilon} )}$ ; we shall refer to this as the strong Hardy-Littlewood prime tuples conjecture.

Remark 14 The even Goldbach conjecture and the prime tuples conjecture are still unsolved. However, if one performs more averaging over additional parameters, the analogous asymptotics to (9) or (10) can be proven in many cases, thus giving some support to the accuracy of the modified Cramér model. For instance, Vinogradov famously established (via the Hardy-Littlewood circle method) the analogue to (9) for the number of representations of a large odd natural number ${N}$ as the sum of three primes, implying in particular that every sufficiently large odd number was the sum of three primes. Similarly, an averaged version of the Hardy-Littlewood conjecture was obtained by Balog, and a general higher-dimensional version of this conjecture in a series of papers by Green, Ziegler, and myself. This allows one to unconditionally establish the asymptotics predicted by the modified Cramér model for statistics such as the number of arithmetic progressions of length ${k}$ consisting solely of primes less than a given threshold ${x}$ .

Exercise 15 (Landau’s fourth problem) Use the modified Cramér model to predict that

$\displaystyle \# \{ n \leq x: n^2 + 1 \in {\mathcal P} \} = {\mathfrak S} \frac{x}{2 \log x}$

where

$\displaystyle {\mathfrak S} := \prod_p \frac{1 - \omega(p) / p}{1-1/p}$

and ${\omega(p)}$ is the number of residue classes ${a\ (p)}$ such that ${a^2 + 1 = 0\ (p)}$ , with ${{\mathfrak S}}$ convergent to a positive non-zero number. (To show the latter claim, you will need quadratic reciprocity (Exercise 59 from Notes 2) and Dirichlet’s theorem on primes in arithmetic progression, in the form of Exercise 81 of Notes 1.) In particular, the modified Cramér model predicts an affirmative answer to Landau’s fourth problem, namely that there are infinitely many ${n}$ such that ${n^2+1}$ is prime.

Remark 16 A common generalisation of the previous two exercises is the Bateman-Horn conjecture, that asserts that given a collection ${P_1,\dots,P_k: {\bf Z} \rightarrow {\bf Z}}$ of distinct non-constant irreducible polynomials that take integer values at the integers, have positive leading coefficients, and such that for every prime ${p}$ there is a natural number ${n}$ such that ${P_1(n),\dots,P_k(n)}$ are not divisible by ${p}$ , one has

$\displaystyle \# \{ n \leq x: P_1(n),\dots,P_k(n) \in {\mathcal P} \} = ({\mathfrak S} +o(1))\frac{x}{D \log^k x}$

as ${x \rightarrow \infty}$ , where ${D}$ is the product of the degrees of the polynomials ${P_1,\dots,P_k}$ , and

$\displaystyle {\mathfrak S} := \prod_p \frac{1 - \omega(p) / p}{(1-1/p)^k}$

where ${\omega(p)}$ is the number of residue classes ${a\ (p)}$ such that ${P_1(a) \dots P_k(a) = 0\ (p)}$ . This can be justified from the modified Cramér model by similar reasoning to the above, although to show that the product ${{\mathfrak S}}$ converges to a non-zero number requires some additional algebraic number theory input (the Chebotarev density theorem, which can be viewed as a generalisation of Dirichlet’s theorem) which we are not covering here. A consequence of the Bateman-Horn conjecture is Schinzel’s hypothesis H, which asserts under the above hypotheses that there are infinitely many natural numbers ${n}$ such that ${P_1(n),\dots,P_k(n)}$ are simultaneously prime.

We saw that the twin prime conjecture asymptotic (Prediction 8) had to be adjusted (to Prediction 11) when the naive Cramér model was replaced by the modified Cramér model. At the other extreme of prime gap behaviour, a somewhat analogous modification of the Cramér conjecture (Conjecture 7) on ${G(X)}$ was shown by Granville:

Prediction 17 (Modified Cramér conjecture) We have ${G(X) \geq (2e^{-\gamma} - o(1)) \log^2 X}$ as ${X \rightarrow \infty}$ .

Since ${2e^{-\gamma} = 1.1229\dots}$ , we thus see that Prediction 8 is now expected to be incorrect by over ten percent. It is uncertain whether the quantity ${2e^{-\gamma}}$ can be improved further, however it seems reasonable to continue to conjecture a weak form ${G(X) \asymp \log^2 X}$ of the Cramér conjecture.

Proof: (Uses modified Cramér model) The basic idea here is not to look at all prime gaps, but gaps associated to given residue classes modulo ${W}$ , for a well chosen choice of ${W}$ . This is an instance of the Maier matrix method, which we will revisit later in this course.

More specifically, fix a small quantity ${\varepsilon > 0}$ . Set ${w := \log X / \log\log X}$ ; the reason for this choice is that this is almost the largest choice that keeps ${W}$ significantly less than ${X}$ , since from the prime number theorem ${\sum_{p \leq w} \log p = (1+o(1)) w}$ one has

$\displaystyle W = \exp( (1+o(1)) w ) = X^{o(1)}. \ \ \ \ \ (12)$

Let

$\displaystyle G'_w(X) := \sup_{n: p'_{n,w}, p'_{n+1,w} \leq X} p'_{n+1,w} - p'_{n,w}$

where ${p'_{1,w}, p'_{2,w}, \dots}$ are the elements of ${{\mathcal P}'_w}$ in increasing order. We will show that almost surely one has ${G'_w(X) \geq (2e^{-\gamma}-O(\varepsilon)) \log^2 X}$ as ${X \rightarrow \infty}$ , which leads to the above prediction by applying the modified Cramér model with this choice of ${w}$ .

By Borel-Cantelli, it suffices to show that ${G(X) \geq (2e^{-\gamma}-O(\varepsilon)) \log^2 X}$ with probability ${1-O_\varepsilon(X^{-2})}$ for sufficiently large ${X}$ . Set ${L := \lfloor (1 - \varepsilon) 2e^{-\gamma} \log^2 X \rfloor}$ . Suppose we can find an natural number ${k}$ between ${X/4W}$ and ${X/2W}$ such that the numbers ${kW+1,\dots,kW+L}$ all lie outside of ${{\mathcal P}'_w}$ . It is easy to see that with probability ${1-O_\varepsilon(X^{-2})}$ there is at least one element of ${{\mathcal P}'_w}$ in ${[X/2,X]}$ , and so we will have ${G'_w(X) \geq L}$ in this case. So it suffices to show that with probability ${1-O_\varepsilon(X^{-2})}$ there is at least one ${k}$ with ${kW+1,\dots,kW+L \not \in {\mathcal P}'_w}$ .

Fix ${k}$ . The key point is that an unusually large number of the elements of the sequence ${kW+1,\dots,kW+L}$ are automatically excluded from ${{\mathcal P}'_w}$ by virtue of having a common factor with ${W}$ ; probabilistic heuristics suggest that at least ${\frac{\phi(W)}{W} L}$ or so of the elements should be coprime, but the truth turns out to be closer to ${\frac{1}{2e^{-\gamma}} \frac{\phi(W)}{W} L}$ , which is ultimately where the gain of ${2e^{-\gamma}}$ over Conjecture 7 is coming from. Indeed, since ${L \leq w^3}$ for ${X}$ large enough (and ${\varepsilon}$ small), we see from the sieve of Erathosthenes that the only elements in this sequence which are coprime to ${W}$ are ${kW + 1}$ , ${kW + p}$ , for primes ${w < p\leq L}$ , and ${kW+pq}$ for primes ${w < p \leq q \leq L}$ . Let us count how many such elements there are. From the prime number theorem there are at most

$\displaystyle (1+o(1)) \frac{L}{\log L} = (1-\varepsilon+o(1)) e^{-\gamma} \frac{\log^2 X}{\log\log X}$

elements of the form ${kW+p}$ . From the prime number theorem again, the number of elements of the form ${kW+pq}$ , noting that ${w \leq p \leq \sqrt{L}}$ and ${q \leq L/p}$ , is at most

$\displaystyle (1+o(1)) \sum_{w \leq p \leq \sqrt{L}} \frac{L/p}{\log(L/p)}.$

By choice of ${w}$ , we have ${\log(L/p) = (1+o(1)) \log \log X}$ for ${p}$ in this sum, so by Mertens’ theorem this contribution is at most

$\displaystyle (1+o(1)) \frac{L}{\log\log X} (\log \log \sqrt{L} - \log\log w)$

which simplifies to

$\displaystyle O( \frac{\log^2 X}{\log\log X \log\log\log X} ).$

Thus the total number of elements in ${kW+1,\dots,kW+L}$ that are coprime to ${W}$ is at most ${(1-\varepsilon+o(1)) e^{-\gamma} \frac{\log^2 X}{\log\log X}}$ . In the modified Cramér model, each of these elements has an independent probability of ${\frac{W}{\phi(W) \log(kW+b)} = (1+o(1)) \frac{W}{\phi(W) \log X}}$ of lying in ${{\mathcal P}'_w}$ . From Mertens’ third theorem we have

$\displaystyle \frac{W}{\phi(W)} = \prod_{p \leq w} (1-\frac{1}{p})^{-1}$

$\displaystyle = (e^{\gamma} + o(1)) \log w$

$\displaystyle = (e^\gamma + o(1)) \log\log X$

and so each of the ${kW+b}$ has an independent probability of ${(e^\gamma + o(1)) \frac{\log\log X}{\log X}}$ of lying in ${{\mathcal P}'_w}$ . The probability that none of the ${kW-L,\dots,kW+L}$ lie in ${{\mathcal P}'_w}$ is thus at least

$\displaystyle (1 - (e^\gamma + o(1)) \frac{\log\log X}{\log X})^{(1-\varepsilon+o(1)) e^{-\gamma} \frac{\log^2 X}{\log\log X}}$

$\displaystyle = \exp( - (e^\gamma + o(1)) \frac{\log\log X}{\log X} \times (1-\varepsilon+o(1)) e^{-\gamma} \frac{\log^2 X}{\log\log X} )$

$\displaystyle = X^{\varepsilon-1+o(1)}.$

These events are independent in ${k}$ , and there are ${\gg \frac{X}{W} = X^{1-o(1)}}$ choices of ${k}$ . Thus the probability that none of these events occurs is at most

$\displaystyle (1 - X^{\varepsilon-1+o(1)})^{X^{1-o(1)}} = \exp( - X^{\varepsilon+o(1)} )$

which is ${O_\varepsilon(X^{-2})}$ as required. $\Box$

— 2. Möbius pseudorandomness —

We now turn to a somewhat different model, which is not based on modeling the set of primes ${{\mathcal P}}$ directly, but rather the Möbius function ${\mu: {\bf N} \rightarrow \{-1,0,+1\}}$ , which we have seen in Notes 1 to be closely related to the distribution of the primes. One can also work with the closely related Liouville function ${\lambda: {\bf N} \rightarrow \{-1,+1\}}$ , if one wants to consider a function consisting of pure sign patterns with no zeroes.

One could adopt a Cramér type model for the Möbius or Liouville functions by replacing them with a random arithmetic function, or perhaps a random multiplicative arithmetic function, taking values in ${\{-1,0,+1\}}$ or ${\{-1,+1\}}$ . While one can certainly do this (see e.g. this paper of Harper for a recent study of such models), we will not directly build such models here, but instead focus on studying linear statistics

$\displaystyle \sum_{n \leq x} \mu(n) f(n) \ \ \ \ \ (13)$

of the Möbius function (or analogous statistics ${\sum_{n \leq x} \lambda(n) f(n)}$ for the Liouville function), tested against various arithmetic functions ${f: {\bf N} \rightarrow {\bf C}}$ of interest. The Möbius and Liouville statistics are closely related, with estimates on one of these sums usually leading quite quickly in practice to analogous estimates on the other sum:

Exercise 18 Establish the identities

$\displaystyle \sum_{n \leq x} \lambda(n) f(n) = \sum_{d \leq \sqrt{x}} \sum_{n \leq x/d^2} \mu(n) f(d^2 n)$

and

$\displaystyle \sum_{n \leq x} \mu(n) f(n) = \sum_{d \leq \sqrt{x}} \mu(d) \sum_{n \leq x/d^2} \lambda(n) f(d^2 n)$

for any arithmetic function ${f: {\bf N} \rightarrow {\bf C}}$ and any ${x > 0}$ . (In practice, due to the absolute convergence of ${\sum_d \frac{1}{d^2}}$ , the summation in ${d}$ is fairly manageable, so as a first approximation the above identities are asserting that ${\sum_{n \leq x} \lambda(n) f(n)}$ and ${\sum_{n \leq x} \mu(n) f(n)}$ have comparable behaviour.)

Henceforth we focus solely on the Möbius statistics. Let us normalise ${f}$ to be bounded in size by ${O(1)}$ , then we have the trivial bound

$\displaystyle \sum_{n \leq x} \mu(n) f(n) = O(x).$

This bound can be sharp if ${f}$ oscillates with the same sign as ${\mu}$ , for instance if ${f}$ is equal to ${\mu}$ itself (or to ${\lambda}$ ). However, in most other situations we expect significant cancellation. One can informally (and imprecisely) summarise this principle as follows:

Principle 19 (Möbius pseudorandomness principle) Let ${x}$ be a large quantity, and let ${f: [1,x] \rightarrow {\bf C}}$ be a function bounded by ${O(1)}$ , which is not deliberately chosen so as to oscillate with the same sign as ${\mu(n)}$ , and has “polynomial complexity” in some sense (e.g. it is defined using parameters that are natural numbers of size ${O(x^{O(1)})}$ . Then we predict one of the following cancellation properties:

(Weak pseudorandomness) One has ${\sum_{n \leq x} \mu(n) f(n) = o(x)}$ as ${x \rightarrow \infty}$ .

(Moderate pseudorandomness) One has ${\sum_{n \leq x} \mu(n) f(n) \ll_A x \log^{-A} x}$ for any ${A>0}$ .

(Strong pseudorandomness) One has ${\sum_{n \leq x} \mu(n) f(n) \ll_\varepsilon x^{1/2+\varepsilon}}$ for any ${\varepsilon>0}$ .

Similarly if we replace ${\mu(n)}$ by ${\mu(P(n))}$ for some non-constant polynomial ${P}$ of degree ${O(1)}$ that takes natural number values on ${[1,x]}$ , and which is of polynomial complexity in the sense that its coefficients are ${O(x^{O(1)})}$ .

Note that unlike the Cramér random model, the Möbius pseudorandomness principle is not explicitly probabilistic in nature; the predictions here are completely deterministic in nature, and do not require any analysis of a random model. However, the principle is certainly compatible with various random models for the Möbius function; for instance, if one models ${\mu}$ by a random function from ${{\bf N}}$ to ${\{-1,0,+1\}}$ that is independent of all functions ${f}$ for which one wishes to apply this principle, then one can justify the strong form of this pseudorandomness principle from the Chernoff inequality (or from arguments similar to that used to justify Prediction 3).

The above principle is imprecise, as we have not formally described what functions ${f}$ are admissible for this principle. One clean formalisation of the principle is the Sarnak conjecture, in which ${f}$ is generated by a zero-entropy dynamical system; see this survey of Sarnak or this previous blog post for more discussion. However, we will stick with the more imprecise form of Principle 19, as it covers some situations that are not strictly included in the Sarnak conjecture.

We have allowed for three levels of possible strength for this principle. The weak form of this principle can actually be established rigorously for a somewhat broad range of functions ${f}$ , but is not particularly useful for applications concerning primes (basically because the primes are so sparse within the integers that any properties about primes one wants to discern will usually be lost in the ${o(x)}$ error). The moderate form of this principle can be rigorously established for a smaller range of functions than the weak form, but the error bounds are strong enough to make non-trivial predictions regarding the primes. The strong form of course gives the best predictions, but has not been proven unconditionally for any non-trivial ${f}$ of number-theoretic interest, although as noted above it is certainly compatible with Cramér type models for ${\mu}$ .

Setting ${f=1}$ in the above principle, we see that the strong Möbius pseudorandomness principle gives

$\displaystyle \sum_{n \leq x} \mu(n) \ll_\varepsilon x^{1/2+\varepsilon}$

which as noted in Exercise 33 of Notes 2 was equivalent to the Riemann hypothesis. Using shifted polynomials ${P(n) := n+x}$ we also obtain the variants

$\displaystyle \sum_{x \leq n \leq x+y} \mu(n) \ll_\varepsilon y^{1/2+\varepsilon} \ \ \ \ \ (14)$

for ${x = O(y^{O(1)})}$ . One could be more ambitious and extend this asymptotic to larger values of ${x}$ , but Cramér-type probabilistic heuristics suggest that if ${x}$ is too large (of exponential size in ${y}$ ), then just from (pseudo)-random fluctuations in the sign patten of the Möbius function, one should eventually end up with a choice of ${x}$ in which all (or most) of the signs of ${\mu(n)}$ for ${x \leq n \leq x+y}$ line up, leading to a failure of (14). However, the probabilistic heuristics indicate that (14) is a reasonable claim to make for ${x}$ restricted to be of polynomial size in ${y}$ . More generally, by using the affine polynomials ${P(n) := q(n + \lfloor x/q \rfloor)+b}$ we arrive at the prediction

$\displaystyle \sum_{x \leq n \leq x+y; n = b\ (q)} \mu(n) \ll_{c,\varepsilon} (y/q)^{1/2+\varepsilon} \ \ \ \ \ (15)$

when ${q \leq y^{1-c}}$ and ${x = O( y^{O(1)} )}$ for some ${c>0}$ .

At the other extreme, the weak form of the Möbius pseudorandomness principle gives

$\displaystyle \sum_{n \leq x} \mu(n) = o(n)$

which as noted in Theorem 58 of Notes 1 is equivalent to the prime number theorem. It should then be unsurprising that the moderate form of the conjecture gives a version of the prime number theorem with an error term better than ${o(x)}$ , but worse than predicted by the Riemann hypothesis:

Prediction 20 One has

$\displaystyle \sum_{n \leq x} \Lambda(n) = x + O_A( x \log^{-A} x)$

for any ${x>2}$ and ${A>0}$ .

Proof: (Uses moderate Möbius pseudorandomness) We use the Dirichlet hyperbola method. Since ${\Lambda = \mu * L}$ , we may write

$\displaystyle \sum_{n \leq x} \Lambda(n) = \sum_{d \leq \sqrt{x}} \mu(d) \sum_{m \leq x/d} \log m + \sum_{m \leq \sqrt{x}} \log m \sum_{\sqrt{x} < d \leq x/m} \mu(d).$

From the moderate Möbius pseudorandomness principle (applied with ${x}$ replaced by ${x/m}$ and ${\sqrt{x}}$ , and then subtracting), we have

$\displaystyle \sum_{\sqrt{x} < d \leq x/m} \mu(d) \ll_A \frac{x}{m} \log^{-A} x$

for any ${A}$ , so the contribution of the second sum can be seen to be

$\displaystyle \ll_A x \log^{1-A} x \times \sum_{m \leq \sqrt{x}} \frac{1}{m} \ll_A x \log^{2-A} x.$

Meanwhile, from Stirling’s formula (see equation (8) of Notes 1) one has

$\displaystyle \sum_{m \leq x/d} \log m = \frac{x}{d} \log \frac{x}{d} - \frac{x}{d} + O( \log x )$

and thus

$\displaystyle \sum_{n \leq x} \Lambda(n) = x ( (\log x-1) \sum_{d \leq \sqrt{x}} \frac{\mu(d)}{d} - \sum_{d \leq \sqrt{x}} \frac{\mu(d) \log d}{d} ) + O_A( x \log^{-A} x ).$

Now from further applications of the Möbius pseudorandomness principle and dyadic decomposition, we see that

$\displaystyle \sum_{d \leq \sqrt{x}} \frac{\mu(d)}{d} = \sum_d \frac{\mu(d)}{d^{1+\varepsilon}} + O_A( \log^{-A} x )$

and

$\displaystyle \sum_{d \leq \sqrt{x}} \frac{\mu(d)\log d}{d} = \sum_d \frac{\mu(d) \log d}{d^{1+\varepsilon}} + O_A( \log^{-A} x )$

for sufficiently small ${\varepsilon>0}$ . But on noting that ${\frac{1}{\zeta(s)} = s-1 + O(|s-1|)^2}$ for ${s}$ near ${1}$ , we see that ${\sum_d \frac{\mu(d)}{d^{1+\varepsilon}}}$ and ${\sum_d \frac{\mu(d) \log d}{d^{1+\varepsilon}}}$ converge to ${0}$ and ${-1}$ respectively as ${\varepsilon \rightarrow 0^+}$ , and the claim follows. $\Box$

Of course, the above prediction already follows from the prime number theorem with classical error term (Corollary 39 of Notes 2). But one can achieve much more general results by using other weights ${f}$ than the constant weight ${f(n)=1}$ in Proposition 19. For instance, since ${\mu(n+2)}$ has no obvious propensity to oscillate with the same sign as ${\mu(n)}$ , we expect to have

$\displaystyle \sum_{n \leq x} \mu(n) \mu(n+2) = o(x)$

from the weak Möbius pseudorandomness principle; more generally, we expect the Chowla conjecture

$\displaystyle \sum_{n \leq x} \mu(n+h_1) \dots \mu(n+h_k) = o(x)$

for any distinct ${h_1,\dots,h_k}$ , and more generally still that

$\displaystyle \sum_{n \leq x} \mu(P_1(n)) \dots \mu(P_k(n)) = o(x)$

whenever ${P_1,\dots,P_k}$ are distinct irreducible polynomials of degree ${O(1)}$ and coefficients ${O(x^{O(1)})}$ that attain natural number values when ${n \leq x}$ . Of course, if one assumes the moderate or strong Möbius pseudorandomness principle one can improve the decay rates ${o(x)}$ here to ${O_A(x \log^{-A} x)}$ or ${O_\varepsilon(x^{1/2+\varepsilon})}$ . Using such asymptotics, one can adapt the justification of Prediction 20 to recover asymptotics such as the twin prime asymptotic in Prediction 11:

Prediction 21 (Improved twin prime asymptotic, again) We have

$\displaystyle \sum_{n \leq x} \Lambda(n) \Lambda(n+2) = 2\Pi_2 x + O_A( x \log^{-A} x )$

for any ${A>0}$ and ${x \geq 2}$ , where ${\Pi_2}$ is the twin prime constant from Prediction 11.

It is not difficult to see that this prediction implies Prediction 11, thus demonstrating some consistency between the modified Cramér model and the Möbius pseudorandomness heuristic. We give further examples of this consistency in the exercises below.

Proof: (uses moderate Möbius pseudorandomness) To avoid some minor complications later in the argument we will restrict the sum over ${n}$ to odd ${n}$ ; this is easily accomplished because the contribution of even ${n}$ is ${O(1)}$ . For odd ${n}$ we have

$\displaystyle \Lambda = \Lambda \chi_0 = - (L \mu \chi_0) * \chi_0, \ \ \ \ \ (16)$

where ${\chi_0(n) := 1_{(n,2)=1}}$ is the principal character of modulus ${2}$ . We can then write the odd contribution to ${\sum_{n \leq x} \Lambda(n) \Lambda(n+2)}$ as

$\displaystyle -\sum_{d,m: dm \leq x} \mu(d) \log(d) \chi_0(d) \chi_0(m) \Lambda(dm+2).$

We first consider the contribution of those ${d}$ with ${d \geq x^{1/3}}$ (say), which we write as

$\displaystyle -\sum_{m \leq x^{2/3}} \sum_{x^{1/3} \leq d \leq x/m} \mu(d) \log(d) \chi_0(d) \chi_0(m) \Lambda(dm+2).$

An application of moderate Möbius pseudorandomness (dividing ${\Lambda(dm+2)}$ by ${\log x}$ to make it bounded) gives

$\displaystyle \sum_{x^{1/3} \leq d \leq x/m} \mu(d) \log(d) \chi_0(d) \chi_0(m) \Lambda(dm+2) \ll_A \frac{x}{m} \log^{-A} x$

for any ${A>0}$ , so the contribution of this case is acceptable. Thus it will suffice to show that

$\displaystyle -\sum_{d,m: dm \leq x; d < x^{1/3}} \mu(d) \log(d) \chi_0(d) \chi_0(m) \Lambda(dm+2)$

$\displaystyle = 2 \Pi_2 x + O_A( x \log^{-A} x ).$

We write the left-hand side as

$\displaystyle \sum_{2 < n \leq x+2} \Lambda(n) f(n-2)$

where

$\displaystyle f(n) := - \sum_{d|n: d < x^{1/3}} \mu(d) \log(d) \chi_0(d) \chi_0(n/d).$

We once again use the expansion (16) to write this as

$\displaystyle - \sum_{d,m: 2 < dm \leq x+2} \mu(d) \log(d) \chi_0(d) \chi_0(m) f(dm-2).$

Using moderate Möbius pseudorandomness again, the contribution of those ${d}$ with ${d \geq x^{1/3}}$ is acceptable, so it suffices to show that

$\displaystyle - \sum_{d,m: 2 < dm \leq x+2; d < x^{1/3}} \mu(d) \log(d) \chi_0(d) \chi_0(m) f(dm-2)$

$\displaystyle = 2 \Pi_2 x + O_A( x \log^{-A} x )$

for any ${A > 0}$ . The left-hand side may be rearranged as

$\displaystyle \sum_{d_1,d_2 < x^{1/3}} \mu(d_1) \log(d_1) \chi_0(d_1) \mu(d_2) \log(d_2) \chi_0(d_2)$

$\displaystyle \sum_{m_1,m_2: d_1m_1+2 = d_2 m_2; d_1 m_1 \leq x} 1.$

As ${d_1,d_2}$ are restricted to be odd, we see that the inner sum vanishes unless ${d_1}$ and ${d_2}$ are coprime. In that case, we see from the Chinese remainder theorem the inner sum is counting the portion of an arithmetic progression of modulus ${2d_1d_2}$ that is less than or equal to ${x}$ , so the inner sum is ${\frac{x}{2d_1 d_2} + O(1)}$ . The contribution of the ${O(1)}$ term is easily seen to be ${O( x^{1/3} x^{1/3} \log x \log x)}$ , which is acceptable, so it suffices to show that

$\displaystyle \sum_{d_1,d_2 < x^{1/3}: (d_1,d_2)=1} \frac{\mu(d_1) \log(d_1) \chi_0(d_1) \mu(d_2) \log(d_2) \chi_0(d_2)}{d_1 d_2} \ \ \ \ \ (17)$

$\displaystyle = 4 \Pi_2 + O_A( \log^{-A} x )$

for any ${A>0}$ .

From moderate Möbius pseudorandomness (applied to either the ${d_1}$ or ${d_2}$ sum, depending on which of ${N_1,N_2}$ is larger) we have

$\displaystyle \sum_{N_1 < d_1 \leq 2N_1; N_2 < d_2 < 2N_2: (d_1,d_2)=1} \frac{\mu(d_1) \log(d_1) \chi_0(d_1) \mu(d_2) \log(d_2) \chi_0(d_2)}{(d_1 d_2)^{1+\varepsilon}}$

$\displaystyle \ll_A \log^{-A} \max(N_1,N_2)$

for any ${N_1,N_2 > 2}$ and any ${A>0}$ , ${\varepsilon > 0}$ ; by dyadic decomposition we may thus approximate the left-hand side of (17) up to acceptable errors by

$\displaystyle \sum_{d_1,d_2: (d_1,d_2)=1} \frac{\mu(d_1) \log(d_1) \chi_0(d_1) \mu(d_2) \log(d_2) \chi_0(d_2)}{(d_1 d_2)^{1+\varepsilon}}$

if ${\varepsilon>0}$ is small enough. But this may be written as

$\displaystyle \frac{\partial^2}{\partial s_1 \partial s_2} F(s_1,s_2)|_{s_1=s_2=1+\varepsilon}$

where

$\displaystyle F(s_1,s_2) := \sum_{d_1,d_2: (d_1,d_2)=1} \frac{\mu(d_1) \chi_0(d_1) \mu(d_2) \chi_0(d_2)}{d_1^{s_1} d_2^{s_2}},$

so it suffices to show that

$\displaystyle \lim_{\varepsilon \rightarrow 0^+} \frac{\partial^2}{\partial s_1 \partial s_2} F(s_1,s_2)|_{s_1=s_2=1+\varepsilon} = 4 \Pi_2. \ \ \ \ \ (18)$

Factoring the series over ${d_1,d_2}$ as an Euler product, we have

$\displaystyle F(s_1,s_2) = \prod_{p>2} ( 1 - \frac{1}{p^{s_1}} - \frac{1}{p^{s_2}} ).$

Comparing this with the Euler product ${\zeta(s)^{-1} = \prod_p (1 - \frac{1}{p^s})}$ , we have

$\displaystyle F(s_1,s_2) = \frac{G(s_1,s_2)}{\zeta(s_1) \zeta(s_2)}$

where

$\displaystyle G(s_1,s_2) := (1-\frac{1}{2^{s_1}})^{-1} (1-\frac{1}{2^{s_2}})^{-1} \prod_{p>2} \frac{ 1 - \frac{1}{p^{s_1}} - \frac{1}{p^{s_2}} }{ 1 - \frac{1}{p^{s_1}} - \frac{1}{p^{s_2}} + \frac{1}{p^{s_1+s_2}} }.$

For ${\hbox{Re}(s_1), \hbox{Re}(s_2) > 1}$ , the second product is absolutely convergent and defines a smooth function in ${s_1,s_2}$ . Thus, ${G}$ extends smoothly to a neighbourhood of ${s_1=s_2=1}$ , and the left-hand side of (18) can then be written (using the fact that ${\zeta}$ has a simple pole of residue ${1}$ at ${s=1}$ ) as ${G(1,1)}$ , which can be easily computed to equal ${4\Pi_2}$ as required. $\Box$

Exercise 22 (Goldbach conjecture again) Use moderate Möbius pseudorandomness to give another justification of the Goldbach conjecture (9); indeed, establish the stronger asymptotic

$\displaystyle \sum_{n \leq N} \Lambda(n) \Lambda(N-n) \ \ \ \ \ (19)$

$\displaystyle = 2 \Pi_2 (\prod_{p > 3: p|N} \frac{p-1}{p-2}) N + O_A( N \log^{-A} N)$

for any even ${N \geq 2}$ and ${A>0}$ . (Hint: here, the condition of coprimality of ${d_1,d_2}$ has to be replaced by a more complicated condition involving ${N}$ , and a denominator of ${\frac{1}{d_1 d_2}}$ has to similarly be replaced by ${\frac{1}{[d_1,d_2]}}$ , where ${[d_1,d_2]}$ is the least common multiple of ${d_1,d_2}$ . Nevertheless, this more complicated expression can still be handled by Euler products as previously. On the plus side, with these complications there is no additional need to introduce the character ${\chi_0}$ .)

Exercise 23 Use moderate Möbius pseudorandomness to give another justification of the Hardy-Littlewood prime tuples conjecture (10); indeed, establish the stronger asymptotic

$\displaystyle \sum_{n \leq x} \Lambda(n+h_1) \dots \Lambda(n+h_k) = {\mathfrak S} x + O_{A,h_1,\dots,h_k}( x \log^{-A} x )$

for any ${A>0}$ and ${x \geq 2}$ , under the hypotheses of Exercise 13.

Exercise 24 Use moderate Möbius pseudorandomness to justify the claim

$\displaystyle \sum_{n \leq x: n = a\ (q)} \Lambda(n) = (1 + O_{c,A}(\log^{-A} x )) \frac{x}{\phi(q)}$

for any primitive residue class ${a\ (q)}$ , ${x \geq 2}$ , and ${A > 0}$ , assuming that ${q \leq x^{1/2-c}}$ for some ${c>0}$ . What goes wrong when ${q}$ is larger than ${x^{1/2}}$ ?

Remark 25 A Cramér type model (using ${q}$ in place of ${W}$ ) predicts the same asymptotic with ${q}$ as large as ${x^{1-c}}$ , rather than ${x^{1/2-c}}$ . This exposes some limitations of the Möbius pseudorandomness principle as formulated in Principle 19, in that it is not cannot obtain some of the asymptotics that Cramér type models can reach, particularly when trying to detect primes in very sparse sets of integers. (For similar reasons, Principle 19 has trouble recovering the asymptotic in Exercise 15; it also does not appear to be an appropriate tool for predicting the size ${G(X)}$ of the largest prime gaps.) One can address this weakness of Principle 19 by assuming a stronger version of pseudorandomness, in which the function ${f}$ is allowed to be concentrated on a sparse set of integers, rather than being uniformly bounded by ${O(1)}$ , but we will not detail this variant here.

Remark 26 Using the above sorts of arguments, one might expect that square root cancellation for Möbius correlations ${\sum_{n \leq x} \mu(n) f(n)}$ (i.e., the strong Möbius pseudorandomness conjecture) might lead to square root error terms for von Mangoldt correlations ${\sum_{n \leq x} \Lambda(n) f(n)}$ . However, this is not always the case. For instance, in Appendix C of this paper of Iwaniec, Luo, and Sarnak, the strong Möbius pseudorandomness conjecture is used to predict an unusual non-square-root cancellation

$\displaystyle \sum_n \Lambda(n) f(n) \eta(n/x) = (c+o(1)) x^{3/4}$

for some non-zero ${c}$ , where ${\eta: {\bf R} \rightarrow {\bf C}}$ is a smooth compactly supported function and

$\displaystyle f(n) := n^{-11/2} \tau(n) e(-2\sqrt{n})$

is a normalised modulated version of the Ramanujan tau function ${\tau}$ (not to be confused with the divisor function ${1*1}$ , which we have called ${\tau}$ in previous notes). This asymptotic does not seem to be easily explainable by a Cramér type model, but is still believed to be accurate, as even the strong Möbius pseudorandomness conjecture appears to be quite reliable in practice (but see the caveat below for the function field analogue).

Remark 27 A huge portion of analytic number theory over the natural numbers has a counterpart in the function field setting, in which the ring of integers ${{\bf Z}}$ is replaced with the ring ${F[t]}$ of polynomials over some finite field ${F}$ , with the notion of primality, Möbius function, etc. modified accordingly. As it turns out, in that setting there is a modification that needs to be made to the Möbius pseudorandomness principle, due to biases in the Möbius function ${\mu(P(n))}$ applied to polynomials ${P: F[t] \rightarrow F[t]}$ in this ring, particularly when the characteristic of ${F}$ divides the degree of ${P}$ . For instance, in characteristic three, the Möbius function of the degree ${12}$ polynomial ${P(n) = n^{12} + (t+1) n^6 + t^4}$ is twice as likely to be ${-1}$ as it is to be ${+1}$ (see Example 3.2 of this paper of Conrad, Conrad, and Gross). Similarly, in an arbitrary finite field ${F}$ , the Möbius function of the degree ${4|F|}$ polynomial ${P(n) = n^{4|F|} + t^{2|F|-1}}$ is never ${-1}$ , despite ${P}$ being irreducible. We refer the reader to the Conrad-Conrad-Gross paper for further discussion of these biases, and how to adjust the pseudorandomness principle to account for them; but we will not discuss the function field setting further in these notes.

— 3. Equidistribution of residues —

We now discuss a model closely related to the Cramér model, concerning the residue classes ${n\ (q)}$ of a randomly chosen large number ${n}$ with respect to various residues ${q}$ . For sake of discussion, let us select ${n}$ uniformly at random from the natural numbers less than ${x}$ , for some large quantity ${x}$ . Each residue class ${a\ (q)}$ then occupies ${\frac{x}{q}+O(1)}$ possible values of ${n}$ , so ${n\ (q)}$ is equal to ${a\ (q)}$ with probability ${\frac{1}{q} + O(\frac{1}{x})}$ . Thus, for ${x}$ large compared to ${q}$ , the residue class ${n\ (q)}$ is approximately uniformly distributed in the cyclic group ${{\bf Z}/q{\bf Z}}$ .

Now we consider the joint distribution of the residue classes ${n\ (q)}$ as ${q}$ varies. From the Chinese remainder theorem, if ${q_1}$ and ${q_2}$ are coprime, then the residue class ${n\ (q_1 q_2)}$ is completely determined by the residue classes ${n\ (q_1)}$ and ${n\ (q_2)}$ . Thus, in principle at least, we only need to consider the joint distribution of ${n\ (q)}$ for moduli ${q}$ that are prime powers ${q=p^j}$ . To simplify the discussion, we will just consider residue classes ${n\ (p)}$ for ${p}$ prime. This is already enough information (in principle, at least) for many questions about the primes. For instance, to determine whether a number ${n}$ between ${\sqrt{x}}$ and ${x-2}$ is a twin prime (in the sense that ${n,n+2}$ are both prime), it is necessary and sufficient that ${n\ (p)}$ avoids the residue classes ${0, -2\ (p)}$ for all ${p \leq \sqrt{x}}$ , thanks to the sieve of Eratosthenes.

If ${p_1,\dots,p_k}$ are distinct primes with product ${p_1 \dots p_k}$ much less than ${x}$ , then by the previous discussion, ${n\ (p_1 \dots p_k)}$ is approximately uniformly distributed in ${{\bf Z}/p_1 \dots p_k {\bf Z}}$ , and so by the Chinese remainder theorem, the residue classes ${n\ (p_1), \dots, n\ (p_k)}$ are approximately jointly independent. But what happens in the opposite case, when ${p_1 \dots p_k}$ is much larger than ${x}$ ? Then ${n\ (p_1 \dots p_k)}$ is not close to uniformly distributed in ${{\bf Z}/p_1 \dots p_k {\bf Z}}$ in any strong sense (such as in the total variation sense), since it only takes ${O(x)}$ of the ${p_1 \dots p_k}$ possible values in ${{\bf Z}/p_1 \dots p_k {\bf Z}}$ . However, one can still hope for the random variables ${n\ (p_1), \dots, n\ (p_k)}$ to be approximately independent in some weak sense, in that various probabilistic statistics of these random variables approximately match what they would be if these random variables were genuinely independent.

For instance, suppose one is interested in predicting the number ${\pi(x,w)}$ of natural numbers less than or equal to ${x}$ which are ${w}$ -rough in the sense that they are not divisible by any prime ${p}$ less than ${w}$ , for some ${1 \leq w \leq x}$ . If we pick ${n}$ uniformly at random from the natural numbers up to ${x}$ , then the probability that ${n}$ is not divisible by any given prime ${p \leq w}$ (i.e., that ${n \neq 0\ (p)}$ ) is approximately ${1-\frac{1}{p}}$ . Assuming that the residue classes ${n\ (p)}$ behave as if they are independent, we then expect that the probability that ${n}$ is not divisible by any of the primes ${p \leq w}$ should be approximately ${\prod_{p \leq w} (1-\frac{1}{p})}$ . Thus we arrive at the naive prediction

$\displaystyle \pi(x,w) \approx x \prod_{p \leq w} (1 - \frac{1}{p}). \ \ \ \ \ (20)$

As it turns out, this prediction works well for small ${w}$ , but becomes inaccurate when ${w}$ is very large. Consider for instance the case ${\sqrt{x} \leq w \leq x}$ . The sieve of Erathosthenes then tells us that ${\pi(x,w)}$ consists precisely of the primes ${p}$ with ${w < p \leq x}$ , thus

$\displaystyle \pi(x,w) = \pi(x) - \pi(w).$

If we have ${w = o(x)}$ (in the asymptotic regime ${x \rightarrow \infty}$ ), then the prime number theorem tells us that

$\displaystyle \pi(x,w) = (1+o(1)) \frac{x}{\log x}. \ \ \ \ \ (21)$

In contrast, Mertens’ third theorem (Theorem 42 of Notes 1) gives

$\displaystyle x \prod_{p \leq w} (1 - \frac{1}{p}) = (1+o(1)) \frac{x}{e^\gamma \log w}. \ \ \ \ \ (22)$

Thus we see that the naive independence prediction is incorrect in the range ${\sqrt{x} \leq w \leq o(x)}$ (except when ${w}$ is close to ${x^{1/e^\gamma}}$ , but one should view this as a numerical coincidence); this failure is sometimes known as the Mertens paradox. In retrospect, one can see this after noting that for any two distinct primes ${\sqrt{x} \leq p,q \leq x}$ , the events that ${n=0\ (p)}$ and ${n=0\ (q)}$ are not independent, since they can hold separately, but not simultaneously. There is a similar issue for slightly smaller primes: for instance, if ${x^{1/3} \leq p_1,p_2,p_3 < \sqrt{x}}$ , the events ${n = 0\ (p_1)}$ , ${n = 0\ (p_2)}$ , ${n = 0\ (p_3)}$ can hold separately, but not simultaneously. As such, one should expect the naive independence prediction to typical fail when ${w \approx x^{1/u}}$ for a bounded exponent ${u = O(1)}$ . This is indeed the case, as worked out in the following exercise (which is the “dual” of Exercise 39 from Notes 1).

Exercise 28 (Density of rough numbers) Let ${x}$ be an asymptotic parameter tending to infinity.

(i) Show that for any fixed ${u>0}$ , one has
$\displaystyle \pi( x, x^{1/u} ) = (\omega(u)+o(1)) \frac{x}{\log x^{1/u}}$

where the Buchstab function ${\omega(u)}$ is defined by the series

$\displaystyle \omega(u) = \frac{1_{1 < u}}{u} + \sum_{j=2}^\infty \frac{1}{j!} \int_{[1,+\infty)^{j-1}} 1_{t_1+\dots+t_{j-1} \leq u-1} \frac{dt_1 \dots dt_{j-1}}{t_1 \dots t_j}$

with the convention that ${t_j = u - t_1 - \dots - t_{j-1}}$ . (Note that for any given ${u}$ that only finitely many of the summands are non-zero; one can also view the first term as the ${j=1}$ term of the summation after carefully working out what zero-dimensional spaces and empty products evaluate to).

(ii) (Delay-differential equation) Show that ${\omega}$ is continuous on ${(0,+\infty)}$ except at ${u=1}$ , continuously differentiable except at ${u=1,2}$ , equals ${0}$ for ${0 \leq u \leq 1}$ and obeys the equation
$\displaystyle \frac{d}{du} \omega(u) = \frac{1}{u} (\omega(u-1)-\omega(u))$

for ${u > 1}$ with ${u \neq 2}$ . Give a heuristic justification for this equation by considering how ${\pi(x,x^{1/u})}$ varies with respect to small perturbations of ${u}$ .

(iii) (Wirsing integral equation) Show that
$\displaystyle u \omega(u) = 1_{(1,\infty)}(u) + \int_0^u 1_{(1,\infty)}(t) \omega(u-t)\ dt.$

Give a heuristic justification for this equation by starting with a ${z}$ -rough number ${n \in [1,x]}$ and considering a factor ${n/p}$ , where ${p}$ is a prime factor of ${n}$ chosen at random with probability ${j \frac{\log p}{\log n}}$ (if ${p}$ occurs ${j}$ times in the prime factorisation of ${n}$ ).

(iv) (Laplace transform) Show that
$\displaystyle \int_0^\infty \omega(u) e^{-su}\ du = \exp( \int_s^\infty \frac{e^{-t}}{t}\ dt ) - 1$

for all ${s > 0}$ .

(v) (Duality with Dickman function) If ${\rho}$ is the Dickman function from Exercise 39 of Notes 1, show that
$\displaystyle 1 = \rho(u) + \int_0^u \rho(t) \omega(u-t)\ dt$

for all ${u>0}$ .

(vi) (Asymptotic constancy) For ${A>0}$ , show that ${\frac{d}{du} \omega(u) \ll_A u^{-A}}$ for all sufficiently large ${u}$ . Conclude in particular that ${\omega(u)}$ converges to a limit as ${u \rightarrow \infty}$ .

(vii) (Limiting value) Show that ${\omega(u)}$ converges to ${e^{-\gamma}}$ as ${u \rightarrow \infty}$ . (Hint: Use (iv) with ${s}$ small, combined with (vi).)

Remark 29 One can model the dependencies of the events ${n = 0\ (p)}$ for large ${p}$ more accurately by using a more sophisticated model than a jointly independent model, namely a Poisson-Dirichlet process, discussed in this previous post. This model can be used for instance to recover for instance the Dickman and Buchstab statistics for smooth and rough numbers respectively, thus also helps explain the ${e^\gamma}$ factor appearing in (22). However, we will not discuss this process further here.

Parts (i) and (vii) of Exercise 28 suggest that the naive prediction (20) is in fact quite accurate for ${w = x^{1/u}}$ with ${u}$ large, even if it becomes inaccurate when ${u}$ is small. We now informally generalise this to a heuristic:

Heuristic 30 (Equidistribution of residues) Let ${w = x^{o(1)}}$ as ${x \rightarrow \infty}$ , and let ${n}$ be chosen uniformly at random from the numbers up to ${x}$ . Then the residues ${n\ (p)}$ for ${p \leq w}$ behave “as if” they were independent random variables. Similarly for other “reasonable” probability distributions on natural numbers up to ${x}$ (e.g. the uniform distribution on natural numbers between ${x/2}$ and ${x}$ ). A similar heuristic can apply for ${w}$ as large as ${x^{1/u}}$ if one is prepared to accept some error terms which go to zero as ${u}$ goes to infinity.

In later notes, we will develop the basics of sieve theory, which provides a number of rigorous interpretations of the above heuristic (such as the fundamental lemma of sieve theory).

Because the heuristic stops working for ${w}$ as large as ${\sqrt{x}}$ or ${x}$ , one cannot use Heuristic 30 directly to count primes to make predictions for problems such as Landau’s problems. However, one can input this heuristic into the modified Cramér model (Model 10), effectively giving the ability to take the ${w}$ parameter in that model to be as large as ${x^{o(1)}}$ . (But, as mentioned before, in many applications the precise choice of the ${w}$ parameter is not terribly important, so long as it is eventually taken to go to infinity.)

Alternatively, by stopping the sieve of Eratosthenes early, one can use Heuristic (30) to predict upper bounds for various prime statistics. For instance, let us return to the problem of counting prime twins ${p, p+2}$ with ${p \leq x}$ . We select a natural number ${n}$ uniformly between ${\sqrt{x}}$ and ${x-2}$ and ask for the probability that ${n,n+2}$ are simultaneously prime (the contribution of those primes below ${\sqrt{x}}$ is negligible). By the sieve of Eratosthenes, this is equivalent to requiring that ${n}$ avoid the residue classes ${0\ (p)}$ , ${-2\ (p)}$ for all ${p \leq \sqrt{x}}$ . We cannot apply the heuristic all the way to ${\sqrt{x}}$ , so let us stop at ${w = x^\varepsilon}$ for some small ${\varepsilon}$ , with the assumption that the error terms will be somehow manageable if ${\varepsilon}$ is small enough. For each ${p \leq w}$ , the probability that ${n}$ avoids both of ${0\ (p)}$ and ${-2\ (p)}$ is ${1-\frac{2}{p}}$ , except when ${p=2}$ , where the probability is ${\frac{1}{2}}$ . Thus, by Heuristic 30, the probability that ${n}$ avoids ${0, -2\ (p)}$ for all ${p \leq w}$ should be approximately

$\displaystyle \frac{1}{2} \prod_{2 < p \leq w} (1 - \frac{2}{p}).$

Writing ${1-\frac{2}{p}}$ as ${(1 - \frac{1}{(p-1)^2}) (1 - \frac{1}{p})^2}$ and recalling the twin prime constant (7), this probability is approximately

$\displaystyle 2 \Pi_2 \prod_{p \leq w} (1 - \frac{1}{p})^2$

which by Mertens’ third theorem is approximately

$\displaystyle \frac{2 \Pi_2}{(e^\gamma \log w)^2},$

leading to an upper bound of approximately ${2\Pi_2 \frac{x}{(e^\gamma \log w)^2}}$ for the number of twin primes up to ${x}$ . As with the problem of counting ${\pi(x,z)}$ , this upper bound fails to recover the predicted asymptotic from Prediction 11 if one naively sets ${w}$ equal to ${\sqrt{x}}$ or ${x}$ , but it is in some sense off “by the same factor” that (22) is off from (21). In particular, if one formally sets ${w}$ equal to the “magic” value of ${x^{1/e^\gamma}}$ , one recovers Prediction 11; the use of this magic value has been proposed by Pólya as a computational trick for arriving at suitable predictions for prime asymptotics up to ${x}$ , though I would be cautious about using this choice of ${w}$ blindly. One can perform an analogous upper bound analysis to the problems considered in Exercises 12, 13, 15; we leave this as an exercise to the interested reader.

— 4. The pair correlation conjecture and the GUE hypothesis —

We now turn to what appears at first glance to be a completely different way to model the primes, via the explicit formula connecting primes with zeroes of the zeta function.

To simplify the exposition, and to obtain the strongest results and predictions, we will work in this section under the assumption of the Riemann hypothesis (Conjecture 28 from Notes 2), which from the functional equation (Theorem 1 from Supplement 3) is equivalent to the assertion that all the non-trivial zeroes ${\rho}$ of the Riemann zeta function ${\zeta}$ lie on the critical line ${\{ s: \hbox{Re}(s) = \frac{1}{2} \}}$ . To emphasise this fact, we will write such zeroes as ${\rho = \frac{1}{2} + i \gamma}$ for various real numbers ${\gamma}$ , known as the ordinates of non-trivial zeroes of the zeta function. All sums over ${\gamma}$ (or ${\gamma_0, \gamma_1}$ , etc.) are understood to be over such ordinates. For the purposes of notational simplicity, we will also assume that the zeroes of ${\zeta}$ are simple, so the ordinates are all distinct; it is not difficult to modify the discussion and notation below to take into account the (unlikely) possibility of repeated zeroes, but we will leave this as an exercise to the interested reader.

The explicit formula connects primes with the ordinates ${\gamma}$ . There are many equivalent ways to express this formula, but we will begin with the smoothed explicit formula (Exercise 46 from Supplement 3), which asserts that

$\displaystyle \sum_n \Lambda(n) g(\log n) = \hat g(-i) - \sum_\gamma \hat g(-i/2 + \gamma)$

$\displaystyle - \sum_n \hat g(2in)$

for any smooth compactly supported ${g}$ supported on ${(0,+\infty)}$ , where ${\hat g(t) := \int_{\bf R} g(u) e^{itu}\ du}$ is the Fourier-Laplace transform. (One could also use the Riemann-Weil explicit formula, see Exercise 47 of Supplement 3, which has the advantage of not requiring ${g}$ to be supported on the positive real axis.) We can get rid of the ${\hat g(-i)}$ and ${\hat g(2in)}$ factors and the inconvenient shift of ${-i/2}$ in the sum over ordinates by introducing the normalised signed measure ${\mu}$ on the real line defined by

$\displaystyle \int_{\bf R} g(u)\ d\mu(u) := \sum_n \frac{\Lambda(n)}{\sqrt{n}} g(\log n) \ \ \ \ \ (23)$

$\displaystyle - \int_0^\infty g(u) (e^{u/2} - \sum_n e^{-(2n+1/2) u})\ du,$

and then the explicit formula (after replacing ${g(u)}$ by ${g(u) e^{-u/2}}$ ) becomes

$\displaystyle \int_{\bf R} g(u)\ d\mu(u) = - \sum_\gamma \hat g(\gamma) \ \ \ \ \ (24)$

for any smooth compactly supported ${g}$ supported on ${(0,+\infty)}$ . This implies a multidimensional analogue

$\displaystyle \int_{{\bf R}^k} g( u_1,\dots, u_k) d\mu(u_1) \dots d\mu(u_k) = (-1)^k \sum_{\gamma_1,\dots,\gamma_k} \hat g(\gamma_1,\dots,\gamma_k) \ \ \ \ \ (25)$

of the explicit formula, where ${k \geq 1}$ and ${g: {\bf R}^k \rightarrow {\bf C}}$ is a smooth compactly supported function supported on ${(0,+\infty)^k}$ , and ${\hat g}$ is now the multidimensional Fourier transform

$\displaystyle \hat g(t_1,\dots,t_k) := \int_{{\bf R}^k} g(u_1,\dots,u_k) e^{i(t_1u_1+\dots+t_ku_k)}\ du_1 \dots du_k.$

Exercise 31 Derive (25) from (24). (Hint: first handle the case when the multidimensional function ${g: {\bf R}^k \rightarrow {\bf C}}$ decomposes as a finite linear combination of tensor products of one-dimensional smooth compactly supported functions supported on ${(0,+\infty)}$ , and use the Stone-Weierstrass theorem and a limiting argument to then obtain the general case. See this paper of Rudnick and Sarnak for a more general version of (25).

One can use (25) with various choices of ${g}$ to relate various correlations between the primes to correlations between ordinates. To illustrate this, let us apply (25) with ${k=2}$ and ${g}$ equal to the function

$\displaystyle g( u_1, u_2 ) := \eta( \frac{u_1}{\log T} ) f( T(u_2-u_1) )$

for some ${T>2}$ (which we view as an asymptotic parameter going to infinity), and ${\eta: {\bf R} \rightarrow {\bf C}, f: {\bf R} \rightarrow {\bf C}}$ are fixed smooth compactly supported functions with ${\eta}$ supported on ${(0,\infty)}$ ; it will be convenient to normalise ${f(0)=1}$ . This may seem like a somewhat arbitrary choice of test function ${g}$ , but informally this choice is measuring a smoothed pair correlation between primes ${p, q}$ of size ${T^{O(1)}}$ which differ by a multiplicative factor of ${1+O(1/T)}$ .

With this choice of ${g}$ , (25) becomes (after a routine change of variables)

$\displaystyle \frac{1}{\log^2 T} \int_{{\bf R}^2} \eta( \frac{u_1}{\log T} ) f( T(u_1-u_2) )\ d\mu(u_1) d\mu(u_2) \ \ \ \ \ (26)$

$\displaystyle = \frac{1}{T \log T} \sum_{\gamma_1,\gamma_2} \hat \eta( \log T (\gamma_1+\gamma_2) ) \hat f( \frac{\gamma_2}{T} ).$

Let us first look at the right-hand side of (26). From conjugation symmetry ${\zeta(\overline{s}) = \overline{\zeta(s)}}$ we see that the ordinates are symmetric around the origin, so on replacing ${\gamma_1}$ with ${-\gamma_1}$ , we can rewrite this expression as

$\displaystyle \frac{1}{T \log T} \sum_{\gamma_2} \hat f( \frac{\gamma_2}{T} ) \sum_{\gamma_1} \hat \eta( 2\pi L (\gamma_2 - \gamma_1 ) )$

where we have introduced the normalising factor ${L := \frac{1}{2\pi} \log T}$ . The significance of this factor comes from the Riemann-von Mangoldt formula (Theorem 40 from Supplement 3), which tells us that the number of ordinates in ${[0,T]}$ is equal to ${(1+o(1)) LT}$ , so the average spacing between ordinates in this interval is approximately ${1/L}$ . The sum ${\sum_{\gamma_1} \hat \eta( 2\pi L (\gamma_2 - \gamma_1 ) )}$ is a smoothed count of ordinates that lie within ${O(1/L)}$ of ${\gamma_1}$ .

We can use the Riemann-von Mangoldt formula to isolate the diagonal term:

Exercise 32 Show that

$\displaystyle \sum_\gamma \hat f(\frac{\gamma}{T}) = (1+o(1)) T \log T.$

The right-hand side of (26) is thus

$\displaystyle \hat \eta(0) + o(1) + \frac{1}{T \log T} \sum_{\gamma_2} \hat f( \frac{\gamma_2}{T} ) \sum_{\gamma_1 \neq \gamma_2} \hat \eta( 2\pi L (\gamma_2 - \gamma_1 ) ).$

Let us now make the hypothesis that the normalised differences ${L (\gamma_2 - \gamma_1)}$ between distinct ordinates ${\gamma_1,\gamma_2}$ of size ${O(T)}$ (as weighted by ${\hat f(\frac{\gamma_2}{T})}$ ) have a limiting density ${\rho_2: {\bf R} \rightarrow {\bf R}^+}$ , in the sense that

$\displaystyle \frac{1}{T \log T} \sum_{\gamma_2} \hat f( \frac{\gamma_2}{T} ) \sum_{\gamma_1 \neq \gamma_2} F( L(\gamma_2 -\gamma_1) ) = \int_{\bf R} \rho_2(t) F(t)\ dt + o(1) \ \ \ \ \ (27)$

for any fixed smooth, rapidly decreasing function ${F}$ ; we refer to ${\rho_2}$ as the pair correlation function. Intuitively, ${\rho_2(t) dt}$ should be thought of as the asymptotic probability that a randomly chosen ordinate ${\gamma_2}$ has another ordinate ${\gamma_1}$ with normalised difference ${L(\gamma_2 - \gamma_1)}$ lying in the interval ${[t,t+dt]}$ if ${dt}$ is infinitesimal. If we assume such an asymptotic, then the right-hand side of (26) is now

$\displaystyle \hat \eta(0) + o(1) + \int_{\bf R} \rho_2(t) \hat \eta(2\pi t)\ dt.$

Since the average spacing between ordinates is ${1/L}$ , we expect ${\rho_2}$ to be asymptotically equal to ${1}$ , at least on average, so we write ${\rho_2}$ as ${1 - (1-\rho_2)}$ . By hypothesis ${\eta(0)=0}$ , so from the Fourier inversion formula we have ${\int_{\bf R} \hat \eta(2\pi t)\ dt = 0}$ . Thus the left-hand side of (26) is now

$\displaystyle \hat \eta(0) + o(1) - \int_{\bf R} (1-\rho_2)(t) \hat \eta(2\pi t)\ dt$

which (assuming ${1-\rho_2}$ is absolutely integrable) can be expressed using Fubini’s theorem as

$\displaystyle \int_{\bf R} \eta(u) (1 - \widehat{1-\rho_2}( 2\pi u ))\ du + o(1). \ \ \ \ \ (28)$

Of course, to make use of this formula we will need to know or conjecture something about the pair correlation function ${\rho_2}$ . To do this we return to the left-hand side of (26). In principle, we can use (23) to rewrite this as an expression involving the von Mangoldt function; very roughly, the left-hand side of (26) is a normalised variance of the error term in the prime number theorem in smoothed out versions of the interval ${[x, x+\frac{x}{T}]}$ with ${\frac{\log x}{\log T}}$ drawn from the support of ${\eta}$ . The second term on the right-hand side in (23) is somewhat annoying to deal with in general, but if ${\eta}$ is supported close enough to the origin then things simplify somewhat:

Proposition 33 If ${\eta}$ is supported in ${(0,2)}$ , then the left-hand side of (26) is equal to

$\displaystyle \frac{1}{\log^2 T} \sum_{n_1,n_2} \frac{\Lambda(n_1) \Lambda(n_2)}{\sqrt{n_1} \sqrt{n_2}} \eta( \frac{\log n_1}{\log T} ) f( T(\log n_1 - \log n_2 ) )$

$\displaystyle - \frac{1}{T \log T} (\int_{\bf R} f(u)\ du) (\int_{\bf R} \eta(u) e^{Tu}\ du) + o(1).$

Proof: By hypothesis, ${\eta}$ is supported on ${[\varepsilon,2-\varepsilon]}$ for some fixed ${\varepsilon>0}$ . In this argument we will allow implied constants to depend on ${f,\eta,\varepsilon}$ .

Expanding out (23), we see that the left-hand side of (26) is the sum of the four terms

$\displaystyle \frac{1}{\log^2 T} \sum_{n_1,n_2} \frac{\Lambda(n_1) \Lambda(n_2)}{\sqrt{n_1} \sqrt{n_2}} \eta( \frac{\log n_1}{\log T} ) f( T(\log n_1 - \log n_2 ) ), \ \ \ \ \ (29)$

$\displaystyle -\frac{1}{\log^2 T} \sum_{n_1} \frac{\Lambda(n_1)}{\sqrt{n_1}} \int_{\bf R} \eta( \frac{\log n_1}{\log T} ) f( T(\log n_1 - u ) ) E(u)\ du, \ \ \ \ \ (30)$

$\displaystyle -\frac{1}{\log^2 T} \sum_{n_2} \frac{\Lambda(n_2)}{\sqrt{n_2}} \int_{\bf R} \eta( \frac{u}{\log T} ) f( T(u - \log n_2) ) E(u)\ du, \ \ \ \ \ (31)$

and

$\displaystyle \frac{1}{\log^2 T} \int_{{\bf R}^2} \eta( \frac{u_1}{\log T} ) f( T(u_1 - u_2) ) E(u_1) E(u_2)\ du_1 du_2, \ \ \ \ \ (32)$

where

$\displaystyle E(u) := e^{u/2} - \sum_n e^{-(2n+1/2) u} = e^{u/2} + O(e^{-5u/2} ).$

We first inspect (32). From the support of ${f}$ and ${\eta}$ we can write

$\displaystyle E(u_1) E(u_2) = e^{u_1} + O( T^{1-\varepsilon/2} )$

on the support of the integrand. The contribution of the ${O(T^{1-\varepsilon/2})}$ error to (32) is ${o(1)}$ , so (32) simplifies after a change of variables to

$\displaystyle \frac{1}{T \log T} (\int_{\bf R} f(u)\ du) (\int_{\bf R} \eta(u) e^{Tu}\ du) + o(1).$

Next we turn to (30). On the support of the integrand we have

$\displaystyle E(u) =\sqrt{n_1} + O( \frac{\sqrt{n_1}}{T} ),$

and the integral vanishes unless ${T^{1+\varepsilon} \ll n_1 \ll T^{2-\varepsilon}}$ . From this we see that the contribution of the ${O( \frac{\sqrt{n_1}}{T} )}$ error is ${o(1)}$ , and (30) simplifies to

$\displaystyle -\frac{1}{T \log^2 T} (\int_{\bf R} f(u)\ du) \sum_{n_1} \Lambda(n_1) \eta( \frac{\log n_1}{\log T} ) + o(1).$

As we are assuming the Riemann hypothesis, we see from Proposition 24 from Notes 2 that

$\displaystyle \sum_{n_1 \leq x} \Lambda(n) = x + O( T^{1-\varepsilon/2} )$

for all ${x}$ in the support of ${\eta(\frac{\log x}{\log T} )}$ . A routine summation by parts then shows that

$\displaystyle \sum_{n_1} \Lambda(n_1) \eta( \frac{\log n_1}{\log T} ) = \int_{\bf R} \eta(\frac{\log x}{\log T} )\ dx + O( T^{1-\varepsilon/2} )$

and so (30) simplifies to

$\displaystyle - \frac{1}{T \log T} (\int_{\bf R} f(u)\ du) (\int_{\bf R} \eta(u) e^{Tu}\ du) + o(1). \ \ \ \ \ (33)$

As for (31), a Taylor expansion gives

$\displaystyle \eta( \frac{u}{\log T} ) E(u) = \eta( \frac{n_2}{\log T} ) \sqrt{n_2} + O( \frac{\sqrt{n_2}}{T} )$

on the support of the integrand, and the integral vanishes unless ${T^{1+\varepsilon} \ll n_1 \ll T^{2-\varepsilon}}$ . We can then repeat the argument used to estimate (30) to obtain the same estimate (33) for (31). Adding together all these estimates, we obtain the claim. $\Box$

We thus arrive at the asymptotic

$\displaystyle \frac{1}{\log^2 T} \sum_{n_1,n_2} \frac{\Lambda(n_1) \Lambda(n_2)}{\sqrt{n_1} \sqrt{n_2}} \eta( \frac{\log n_1}{\log T} ) f( T(\log n_1 - \log n_2 ) ) \ \ \ \ \ (34)$

$\displaystyle = \frac{1}{T \log T} (\int_{\bf R} f(u)\ du) (\int_{\bf R} \eta(u) e^{Tu}\ du)$

$\displaystyle + \int_{\bf R} \eta(u) (1 - \widehat{1-\rho_2}( 2\pi u ))\ du + o(1)$

whenever ${\eta, f: {\bf R} \rightarrow {\bf C}}$ are fixed functions with ${f(0)=1}$ and ${\eta}$ supported in ${(0,2)}$ . We can use this relation to try to recover the pair correlation function ${\rho_2}$ , or at least the portion of this function described by the Fourier transform ${1 - \widehat{1-\rho_2}( 2\pi u )}$ with ${u \in [0,2]}$ .

We first deal with the easy case when ${\eta}$ is in fact supported on ${(0,1)}$ :

Proposition 34 (Easy case) If ${\eta}$ is supported on ${(0,1)}$ , then the left-hand side of (34) is equal to

$\displaystyle \int_{\bf R} \eta(u) u\ du + o(1).$

Note that when ${\eta}$ is supported on ${(0,1)}$ , the first term on the right-hand side of (34) is ${o(1)}$ , and so this proposition indicates that

$\displaystyle \widehat{1-\rho_2}(2\pi u) = 1-u$

for ${0 < u < 1}$ .

Proof: By hypothesis, ${\eta}$ is supported in ${[\varepsilon,1-\varepsilon]}$ for some fixed ${\varepsilon>0}$ . The summand in the left-hand side of (34) vanishes unless ${n_1 \ll T^{1-\varepsilon}}$ and ${n_2 = (1+O(1/T)) n_1}$ , which implies that ${n_2 - n_1 = o(1)}$ . But ${n_1,n_2}$ are natural numbers, and so (for ${T}$ large enough) this forces ${n_1=n_2}$ . Thus the left-hand side of (34) simplifies (using the normalisation ${f(0)=1}$ ) to

$\displaystyle \frac{1}{\log^2 T} \sum_{n} \frac{\Lambda(n)^2}{n} \eta( \frac{\log n}{\log T} ).$

The contribution of those ${n}$ that are prime powers ${p^j}$ for ${j \geq 2}$ is easily seen to be ${o(1)}$ , so we can write this expression as

$\displaystyle \sum_{p} \frac{1}{p} (\frac{\log p}{\log T})^2 \eta( \frac{\log p}{\log T} ) + o(1).$

The claim now follows from Exercise 37 of Notes 1. $\Box$

Now we look at the complementary case when ${\eta}$ is supported on ${(1,2)}$ , and thus on ${[1+\varepsilon,2-\varepsilon]}$ for some fixed ${\varepsilon>0}$ . (This skips over a transitional case when ${\eta}$ is supported near ${1}$ , but it turns out that the analysis there is basically a mixture of the two other cases, and is left as an exercise to the reader below.) This is significantly more difficult, because ${n_1,n_2}$ are no longer forced to be equal. As such, we are unable to compute the left-hand side of (34) just from the Riemann hypothesis; we will need an even stronger claim, namely the strong Hardy-Littlewood prime tuples conjecture (11) (or more precisely, the ${k=2}$ case of this conjecture) to make headway.

The diagonal contribution ${n_1=n_2}$ to the left-hand side of (34) can still be computed to be ${\int_{\bf R} \eta(u) u\ du + o(1)}$ by the arguments used to prove Proposition 34, so we focus on the contribution of the off-diagonal term ${n_2 \neq n_1}$ . We can write ${n_2 = n_1 + h}$ with ${h}$ non-zero, arriving at

$\displaystyle \frac{1}{\log^2 T} \sum_{h \in {\bf Z} \backslash \{0\}} \sum_n \frac{\Lambda(n) \Lambda(n+h)}{\sqrt{n} \sqrt{n+h}} \eta( \frac{\log n}{\log T} ) f( T \log(1+\frac{h}{n}) ).$

Note that the summand vanishes unless ${T^{1+\varepsilon} \ll n \ll T^{2-\varepsilon}}$ and ${|h|T \ll n}$ , so that ${|h| \ll T^{1-\varepsilon}}$ . By Taylor expansion, we then have

$\displaystyle f( T \log(1+\frac{h}{n}) ) = f( \frac{hT}{n} ) + O( \frac{1}{T} )$

and

$\displaystyle \frac{1}{\sqrt{n} \sqrt{n+h}} = (1 + O(\frac{1}{T}) \frac{1}{n}.$

The contribution of the ${O( \frac{1}{T} )}$ errors can be easily seen to be ${o(1)}$ , so the off-diagonal contribution to (34) simplifies to

$\displaystyle \frac{1}{\log^2 T} \sum_{h {\bf Z} \backslash \{0\}} \sum_n \Lambda(n) \Lambda(n+h) \frac{\eta( \frac{\log n}{\log T} ) f( \frac{hT}{n} )}{n} + o(1).$

Now, the strong Hardy-Littlewood prime tuples conjecture gives

$\displaystyle \sum_{n \leq x} \Lambda(n) \Lambda(n+h) = {\mathfrak S}_h x + O( x^{1/2 + \varepsilon/4} )$

(say) for any ${x \geq T}$ and non-zero ${h}$ with ${|h| \ll T^{1-\varepsilon}}$ , where ${{\mathfrak S}_h}$ is the singular series

$\displaystyle {\mathfrak S}_h := \prod_p \frac{1 - \frac{2}{p} + \frac{1_{p|h}}{p}}{(1-\frac{1}{p})^2}.$

A summation by parts then lets us write ${\sum_n \Lambda(n) \Lambda(n+h) \frac{\eta( \frac{\log n}{\log T} ) f( \frac{hT}{n} )}{n}}$ as the sum of the integral

$\displaystyle {\mathfrak S}_h \int_0^\infty \frac{\eta( \frac{\log x}{\log T} ) f( \frac{hT}{x} )}{x}\ dx$

and the error term

$\displaystyle O( \int_0^\infty x^{1/2+\varepsilon/4} | \frac{d}{dx} (\frac{\eta( \frac{\log x}{\log T} ) f( \frac{hT}{x} )}{x}) |\ dx ).$

For the error term, the derivative can be computed to be ${O(1/x^2)}$ , and vanish unless ${x \gg |h|T}$ , so the error term is ${O( (|h| T)^{-1/2+\varepsilon/4} )}$ , and then summing over non-zero ${|h| \ll T^{1-\varepsilon}}$ we see that this contribution is ${o(1)}$ . Thus the off-diagonal contribution has simplified (after some rearranging) to

$\displaystyle \frac{1}{\log^2 T} \int_0^\infty \eta( \frac{\log x}{\log T} ) (\sum_{{\bf Z} \backslash \{0\}} {\mathfrak S}_h f( \frac{hT}{x} ))\ \frac{dx}{x} + o(1).$

To proceed further we need to understand mean values of the singular series ${{\mathfrak S}_h}$ . It turns out (as first observed by Bombieri and Davenport, and then generalised by Gallagher) ${{\mathfrak S}_h}$ has average value of ${1}$ , (see e.g. this paper of Ford for a short proof, related to the equidistribution of residues heuristics discussed previously). However, for our analysis we will need a finer estimate that detects a deviation from ${1}$ coming from the exclusion of ${h=0}$ from the sum (where the singular series is undefined). Namely:

Proposition 35 (Mean value of singular series) Let ${x \geq 2}$ , and let ${f: {\bf R} \rightarrow {\bf C}}$ be a fixed smooth, compactly supported function. Then

$\displaystyle \sum_{h \neq 0} {\mathfrak S}_h f( \frac{h}{x} ) = (\int_{\bf R} f(u)\ du) x - f(0) \log x + O(1). \ \ \ \ \ (35)$

Informally, the ${-f(0) \log x}$ term here is reflecting a very slight but non-trivial repulsion estimate among the primes (detected by the modified Cramér model, but not the naive Cramér model): if ${n}$ is prime, and ${h}$ is small and non-zero, then ${n+h}$ is slightly less likely to be prime than a typical number of size ${\sim n}$ . This is because most small primes ${q}$ will not divide either ${n}$ or ${h}$ , and so will be slightly more likely to divide ${n+h}$ than a typical number of this size. (Conversely, the small primes ${q}$ that do divide ${h}$ will increase the probability that ${n+h}$ is prime, but because ${h}$ is restricted to be non-zero, this latter effect is slightly weaker than the former.)

Proof: We allow implied constants to depend on ${f}$ . Since ${{\mathfrak S}_h}$ vanishes for odd ${h}$ , we can restrict attention to even ${h}$ . We can then factor

$\displaystyle {\mathfrak S}_h = 2 \Pi_2 \prod_{p|h, \hbox{ odd}} (1 + \frac{1}{p-2})$

where ${\Pi_2}$ is the twin prime constant (7) (cf. (9)). This can then be expanded as

$\displaystyle {\mathfrak S}_h = 2 \Pi_2 \sum_d g(d)$

where ${g}$ is the multiplicative function supported on square-free numbers with ${g(2):=0}$ and ${g(p) := \frac{1}{p-2}}$ for ${p>2}$ . Writing ${h=dn}$ , we may therefore write the left-hand side of (35) as

$\displaystyle 2\Pi_2 \sum_d g(d) \sum_{n \in {\bf Z} \backslash \{0\}, \hbox{ even}} f( \frac{n}{x/d} ).$

The summand vanishes unless ${d = O(x)}$ . In this regime, we may apply Exercise 11 of Notes 1 (or the Poisson summation formula, see Exercise 35 of Supplement 2) and restore the ${n=0}$ term to conclude that

$\displaystyle \sum_{n \in {\bf Z} \backslash \{0\}, \hbox{ even}} f( \frac{n}{x/d} ) = \frac{x}{2d} (\int_{\bf R} f(u)\ du) - f(0) + O( \frac{d}{x} ).$

Noting that ${g(p) \leq \frac{1}{\sqrt{p}}}$ whenever ${p}$ is sufficiently large, we see that ${g(d) \ll d^{-1/2}}$ . From this we see that the contribution of the ${O(\frac{d}{x})}$ term is ${O_\varepsilon( 1 )}$ . The left-hand side of (35) is now

$\displaystyle \frac{\Pi_2}{x} \sum_{d \ll x} \frac{g(d)}{d} + 2\Pi_2 f(0) \sum_{d \ll x} g(d) + O(1).$

Using the bound ${g(d) \ll_\varepsilon d^{-1+\varepsilon}}$ again, we see that ${\sum_{d \ll x} \frac{g(d)}{d} = \sum_d \frac{g(d)}{d}}$ ; also, from Theorem 27 of Notes 1 (with ${k=1}$ ) we have

$\displaystyle \sum_{d \ll x} g(d) = [\frac{1}{2} \prod_{p>2} (1-\frac{1}{p}) (1 + \frac{1}{p-2})] \log x + O(1).$

From (7) we have

$\displaystyle \prod_{p>2} (1-\frac{1}{p}) (1 + \frac{1}{p-2})= \Pi_2^{-1}$

and from Euler products we have

$\displaystyle \sum_d \frac{g(d)}{d} = \prod_{p>2} (1 + \frac{1}{p(p-2)}) = \Pi_2^{-1}$

and the claim follows. $\Box$

We insert this proposition into the previous asymptotic. The contribution of the ${O(1)}$ error in (35) is easily seen to be ${o(1)}$ , so the off-diagonal contribution to (34) is now

$\displaystyle \frac{1}{\log^2 T} \int_0^\infty \eta( \frac{\log x}{\log T} ) ( (\int_{\bf R} f(u)\ du) \frac{x}{T} - \log \frac{x}{T} )\ \frac{dx}{x} + o(1),$

where we have used the normalisation ${f(0)=0}$ . The contribution of the ${(\int_{\bf R} f(u)\ du) \frac{x}{T}}$ term can be written after a change of variables as

$\displaystyle \frac{1}{T \log T} (\int_{\bf R} f(u)\ du) (\int_{\bf R} \eta(u) e^{Tu}\ du),$

that is to say the first term of (34). A similar change of variables expresses the contribution of the ${\log \frac{x}{T}}$ term as

$\displaystyle - \int_{\bf R} \eta(u) (u-1)\ du.$

Combining this with the diagonal contribution of ${\int_{\bf R} \eta(u) u\ du + o(1)}$ to (34) computed previously, we conclude (on the strong Hardy-Littlewood prime tuples conjecture) that the left-hand side of (34) is equal to

$\displaystyle \frac{1}{T \log T} (\int_{\bf R} f(u)\ du) (\int_{\bf R} \eta(u) e^{Tu}\ du) + \int_{\bf R} \eta(u)\ du + o(1)$

when ${\eta}$ is supported on ${(1,2)}$ .

Exercise 36 Assuming the strong Hardy-Littlewood prime tuples conjecture, obtain the combined formula

$\displaystyle \frac{1}{T \log T} (\int_{\bf R} f(u)\ du) (\int_{\bf R} \eta(u) e^{Tu}\ du)$

$\displaystyle + \int_{\bf R} \eta(u) \max(u,1)\ du + o(1)$

for the left-hand side of (34) when ${\eta}$ is supported on ${(0,2)}$ .

By interchanging ${\gamma_1}$ and ${\gamma_2}$ in (27) one sees that the asymptotic pair correlation function ${\rho_2}$ should be even. If one compares the above exercise with (34), one arrives at the prediction

$\displaystyle \widehat{(1-\rho_2)}(2\pi u) = \max( 1 - |u|, 0 ) \ \ \ \ \ (36)$

for all ${|u| < 2}$ ; the justification provided for this prediction requires the strong Hardy-Littlewood prime tuples conjecture when ${1 \leq |u| < 2}$ , but is unconditional for ${|u| < 1}$ .

Remark 37 If one uses the strong Möbius pseudorandomness principle (see Principle 19) in place of the strong Hardy-Littlewood prime tuples conjecture, one will also recover (36), but in a range intermediate between ${\{ |u| < 1 \}}$ and ${\{ |u| < 2 \}}$ , due to some inefficiencies in deploying this principle to study the primes, as discussed in Remark 26. The moderate or weak Möbius pseudorandomness principles do not appear to give any improvement over the easy range ${\{ |u| < 1 \}}$ , except possibly to clarify some endpoint behaviour at ${|u|=1}$ ; this is because the term we are trying to isolate in (34), namely the second term on the right-hand side, is dominated by the first term on the right-hand side when ${|u| > 1}$ , and so very strong asymptotics are needed in order to discern this lower order behaviour. It seems of interest though to come up with a stronger version of Möbius pseudorandomness (possibly involving multidimensional sums rather than just one-dimensional sums) that could recover (36) in the full range ${|u| < 2}$ , or possibly even beyond.

Based on a similar calculation to the above, Montgomery conjectured that (36) should in fact hold for all ${u}$ , not just for ${|u| < 2}$ . Using Fourier inversion, this leads to a prediction

$\displaystyle \rho_2(t) = 1 - (\frac{\sin(\pi t)}{\pi t})^2 \ \ \ \ \ (37)$

for the pair correlation function for all ${t \in {\bf R}}$ , with the convention that the sinc function ${\frac{\sin x}{x}}$ equals ${1}$ when ${x=0}$ . Note that ${\rho_2(t)}$ vanishes to second order as ${t \rightarrow 0}$ ; this indicates a strong repulsion effect between ordinates (far stronger than the weak repulsion between primes discussed previously), asserting roughly speaking that the probability that the gap ${\gamma_{i+1} - \gamma_i}$ between adjacent ordinates is less than ${\varepsilon/L}$ decays like ${\varepsilon^3}$ , rather than the naive prediction of ${\varepsilon}$ which would occur if there was no repulsion phenomenon.

Exercise 38 Formally derive (37) from the hypothesis that (36) holds for all ${u}$ .

We informally refer to the prediction (37) for all ${u \in {\bf R}}$ as the pair correlation conjecture. Actually, because the above analysis only assumes the asymptotic (27) for smooth compactly supported ${\eta}$ , we have only been working thus far with a smoothed version of the pair correlation conjecture. In the literature, stronger versions of the pair correlation conjecture (replacing ${\eta}$ with rougher cutoffs) are sometimes formulated; also, in some conventions, a Dirac mass ${\delta(t)}$ is added to ${\rho_2}$ in order to remove the restriction ${\gamma_1 \neq \gamma_2}$ of distinct ordinates; as such, one should view the pair correlation conjecture as a family of closely related conjectures, rather than a single conjecture (cf. the Möbius pseudorandomness principle, Principle 19). With such strengthenings of the pair correlation conjecture, one can obtain asymptotics for rougher expressions than (26). For instance, we have the following elegant result of Goldston: assuming the Riemann hypothesis, the statement

(Pair correlation conjecture) One has
$\displaystyle \sum_{0 \leq \gamma_1 < \gamma_2 \leq T: \gamma_2 - \gamma_1 \leq \frac{K}{L}} 1 = (1+o(1)) TL \int_0^K 1 - (\frac{\sin(\pi t)}{\pi t})^2\ dt \ \ \ \ \ (38)$

as ${T \rightarrow \infty}$ for any fixed ${K > 0}$ .

is logically equivalent to the statement

(Variance asymptotic for prime number theorem in short intervals) One has
$\displaystyle \int_0^{T^\beta} (\psi(x+x/T) - \psi(x)-x/T)^2 \frac{dx}{x^2} \ \ \ \ \ (39)$

$\displaystyle = (\frac{\beta^2}{2} 1_{\beta < 1} + (\beta - \frac{1}{2}) 1_{\beta \geq 1} + o(1)) \frac{\log^2 T}{T}$

as ${T \rightarrow \infty}$ for any fixed ${\beta > 0}$ , where ${\psi(x) := \sum_{n \leq x} \Lambda(n)}$ is the von Mangoldt summatory function.

which cleanly illustrates the duality between correlations of ordinates and correlations of primes. The implication of (39) from (38) was previously obtained by Gallagher and Mueller. See also this paper of Goldston and Montgomery for a similar equivalence (in which both of the above statements are replaced by slightly stronger versions with less averaging), as well as this paper of Keating. One should view the above variance asymptotic as a prediction that the statistic ${\sum_{x < n \leq x+x/T} \Lambda(n)}$ for ${x \sim T^\beta}$ has variance about ${\min(\beta,1) \frac{x}{T} \log T}$ for ${\beta > 0}$ . (Note that ${\min(\beta,1)}$ is the derivative of ${\frac{\beta^2}{2} 1_{\beta < 1} + (\beta - \frac{1}{2}) 1_{\beta \geq 1}}$ .) In contrast, the naive Cramér model predicts a variance of approximately ${\beta \frac{x}{T} \log T}$ ; there is a variance saturation effect expected for ${\beta > 1}$ which is coming from the slight repulsion between nearby primes discussed previously; this is a further manifestation of the slight “subrandom” nature of the primes, as discussed in Remark 6. See this survey of Goldston for a further discussion of these results; see also this paper of Montgomery and Soundarajan for a more refined analysis, predicting a central limit theorem for the prime number theorem in short intervals that is consistent both with the refined Cramér model and the GUE hypothesis (see below).

Exercise 39 Modify the proof of Proposition 34 to verify (39) unconditionally for ${0 < \beta < 1}$ .

The pair correlation conjecture is also supported by substantial numerical evidence, notably through the computations of Andrew Odlyzko and his co-authors.

It was famously observed by Freeman Dyson, in a tea-time conversation with Hugh Montgomery at the institute for advanced study, that the pair correlation function (37) predicted for ordinates of the zeta function also appeared as the pair correlation function for many models of random matrix theory. Here is one typical such place where it appears:

Theorem 40 (Pair correlation for GUE) Let ${N}$ be a natural number going to infinity, and let ${M_N}$ be an ${N \times N}$ Hermitian random matrix whose diagonal entries are independent real Gaussians of mean zero and variance ${1/N}$ , and whose strictly upper triangular entries are independent complex Gaussians of mean zero and variance ${1/N}$ (independent of the diagonal entries); this random matrix ensemble is known as the Gaussian unitary ensemble (GUE). Let ${\lambda_1 \leq \dots \leq \lambda_N}$ be the (necessarily real) eigenvalues of ${M_N}$ , counted with multiplicity. Let ${E \in (-2,2)}$ be fixed, and define the normalisation factor ${L := \sqrt{4-E^2} N}$ . Then we have

$\displaystyle \sum_{E \leq \lambda_i < \lambda_j \leq E + K/L: L(\lambda_j - \lambda_i) \leq \beta} 1 = (\int_0^\beta \rho_2(u)\ du + o(1)) K$

for any fixed ${\beta>0}$ whenever ${K = K(N)}$ goes to infinity slower than ${N}$ , and where ${\rho_2}$ is the function (37).

See this previous blog post for a proof of this claim. The factor of ${\sqrt{4-E^2}}$ reflects the famous Wigner semicircular law for the GUE ensemble, which does not directly appear in the theory of ordinates of zeta (the nearest analogue is the Riemann-von Mangoldt formula). But the appearance of the pair correlation function (37) does not appear to be closely tied with bulk distribution laws such as the Wigner law. For instance, here is another occurrence of the pair correlation function (37) in random matrix theory that does not involve the semicircle law:

Theorem 41 (Pair correlation for CUE) Let ${N}$ be a natural number going to infinity, and let ${U_N}$ be an ${N \times N}$ unitary random matrix chosen using Haar measure; this random matrix ensemble is known as the circular unitary ensemble (CUE). Let ${e^{i \theta_1},\dots,e^{i\theta_N}}$ be the (necessarily unitary) eigenvalues of ${U_N}$ , counted with multiplicity, with ${0 \leq \theta_1 \leq \dots \leq \theta_N \leq 2\pi}$ . Let ${E \in [0,2\pi)}$ be fixed, and define the normalisation factor ${L := \frac{N}{2\pi}}$ . Then we have

$\displaystyle \sum_{E \leq \theta_i < \theta_j \leq E + K/L: L(\theta_j - \theta_i) \leq \beta} 1 = (\int_0^\beta \rho_2(u)\ du + o(1)) K$

for any fixed ${\beta>0}$ whenever ${K = K(N)}$ goes to infinity slower than ${N}$ , and where ${\rho_2}$ is the function (37).

Proof: This is a result of Dyson. $\Box$

In fact, the pair correlation function ${\rho_2}$ arises in extremely broad classes of random matrices, reflecting a general phenomenon now known as random matrix universality; see this previous blog post for some non-technical discussion of this phenomenon.

This result inspired a more general GUE hypothesis, which broadly speaking asserts that the (suitably normalised) distribution of ordinates of size ${O(T)}$ at the “microscopic” scale of ${1/L}$ (or at the “mesoscopic” scale between ${1/L}$ and ${o(1)}$ ) as ${T \rightarrow \infty}$ should asymptotically attain the same limit as the analogous (suitably normalised) asymptotics of the eigenvalues of GUE (or CUE) at the analogous microscopic or mesoscopic scales as ${N \rightarrow \infty}$ . (Roughly speaking, ${N}$ is analogous to ${\log T}$ , as can be seen by comparing the normalising factors ${L}$ in all of the above examples.) An analogous hypothesis has also been made for other ${L}$ -functions, although in some cases the GUE model needs to be replaced by another standard random matrix model; see this expository article of Katz and Sarnak for details. As such, rigorous results about the asymptotic distribution of eigenvalues of GUE or CUE can be used to make predictions about the distribution of ordinates, which through the explicit formula can also lead to predictions about prime numbers.

For instance, the theory of ensembles such as GUE and CUE in fact provides control not just of pair correlations such as

$\displaystyle \sum_{E \sqrt{N} \leq \lambda_i < \lambda_j \leq E \sqrt{N} + K/L: L(\lambda_j - \lambda_i) \leq \beta} 1,$

but of higher order correlations involving ${k}$ -tuples ${\lambda_{i_1},\dots,\lambda_{i_k}}$ of nearby eigenvalues for ${k \geq 2}$ . We will not state the precise results here, but remark simply that the role of the two-point correlation function ${\rho_2}$ from (37) is replaced by the more general function

$\displaystyle \rho_k(u_1,\dots,u_{k-1}) := \hbox{det}( \frac{\sin(\pi(u_i-u_j))}{\pi(u_i-u_j)} )_{0 \leq i,j \leq k-1} \ \ \ \ \ (40)$

with the convention that ${u_0 := 1}$ . Again, we refer the interested reader to this previous blog post for the relationship between these correlation functions and the GUE ensemble. The determinantal structure of the ${k}$ -point correlation function ${\rho_k}$ is an example of the correlation function of a more general class of determinantal point processes, discussed in this previous blog post.

The ${k}$ -point correlation asymptotics for GUE or CUE leads to one precise instance (but certainly not the only such instance) of the GUE hypothesis:

Prediction 42 (GUE hypothesis) Let ${k \geq 2}$ be fixed, and let ${F: {\bf R}^{k-1} \rightarrow {\bf C}}$ be a smooth compactly supported function. Let ${T \geq 2}$ be an asymptotic parameter going to infinity, and set ${L := \frac{1}{2\pi} \log T}$ . Then

$\displaystyle \sum_{\gamma_1,\dots,\gamma_k \in [0,T], \hbox{ distinct}} F( L(\gamma_2-\gamma_1), \dots, L(\gamma_k-\gamma_1))$

$\displaystyle = LT ( \int_{{\bf R}^n} F(u_1,\dots,u_{k-1}) \rho_k(u_1,\dots,u_{k-1})\ du_1 \dots u_{k-1} + o(1))$

where ${\rho_k}$ is defined by (40).

Much as the pair correlation conjecture leads (via the explicit formula) to asymptotics about pairs of primes ${p, q}$ that are close to each other, the more general GUE hypothesis turns out to lead to asymptotics about pairs of products of primes ${p_1 \dots p_j, q_1 \dots q_{k-j}}$ of primes (for some ${1 \leq j \leq k-1}$ ) that are close to each other, although the precise description of such asymptotics becomes somewhat messy; see this paper of Rodgers for a precise formulation. One can then develop an analogue of Proposition 34 to obtain a partial verification of the GUE hypothesis (essentially verifying that the low frequency component of (40) is correct); this was done (in great generality, for a much wider class of ${L}$ -functions than just the Riemann zeta function, and assuming GRH in place of RH) by Rudnick and Sarnak (with some earlier results by Hejhal). The analogous deployment of the strong Hardy-Littlewood tuples conjecture to verify a larger portion of the GUE hypothesis was carried out by Montgomery and Soundararajan. A heuristic derivation of the entire GUE hypothesis along these lines (without rigorous treatment of error terms) was carried out by Bogomolny and Keating. A function field analogue of the GUE hypothesis, in which the integers ${{\bf Z}}$ are replaced by a function field ${\mathbf{F}_q[t]}$ for some large ${q}$ , was also established by Katz and Sarnak.

As mentioned above, Prediction 42 is not the only way to formalise the GUE hypothesis. The GUE hypothesis can be used to predict the behaviour of the Riemann zeta function ${\zeta}$ , by drawing an analogy between this function and the characteristic polynomial of a GUE or CUE matrix. This can be used for instance to predict central limit theorems for the logarithm of the zeta function, or asymptotics for moments of the zeta function (or its logarithm, or logarithmic derivative) on or near the critical line; furthermore, in the few cases where these predictions can actually be verified rigorously (or on hypotheses such as the Riemann hypothesis), the predictions agree with the rigorous computations. There is now a vast literature on this topic; see for instance this survey of Keating and Snaith for further discussion.

Remark 43 Using the analogy between the statistics of the zeta function and random matrix theory, the Riemann hypothesis is then analogous to the trivial fact that the eigenvalues of a GUE matrix are all real (or that the eigenvalues of a CUE matrix all lie on the unit circle). This is reminiscent of an old idea of Hilbert and Pólya that the ordinates of zeta should arise as the eigenvalues of some “natural” unbounded linear operator on a Hilbert space, which could then be shown to be self-adjoint in order to verify the Riemann hypothesis. Unfortunately, the GUE hypothesis does not suggest a useful candidate for such an operator. In fact, the breadth of the universality phenomenon extends well beyond random matrix models, and so the GUE hypothesis may not actually indicate any direct connection between zeta and matrices (or linear operators), instead reflecting the universal nature of the correlation functions (40).

Remark 44 As with all of the other models discussed in these notes, one should bear in mind that there are finer adjustments to the GUE hypothesis that need to be made in certain regimes. For instance, it appears that there is a very slight repulsion effect between differences ${\gamma_1-\gamma_2}$ of two large ordinates ${\gamma_1,\gamma_2}$ and one small ordinate ${\gamma_0}$ , in that ${\gamma_1-\gamma_2}$ is slightly less likely to be close to ${\gamma_0}$ than a direct application of the GUE hypothesis (or Riemann-von Mangoldt law) would indicate. This repulsion was first observed by Bogolmony and Keating, and is ultimately a reflection of the obvious negative correlation between ${\Lambda^2}$ and ${-\Lambda}$ ; see the papers of Snaith or of Rodgers for further discussion.

79 comments

Comments feed for this article

3 March, 2019 at 7:48 am

Anonymous

Mr.Tao thanks to see this work about k-tuple conjecture:
https://math.stackexchange.com/questions/3133443/weak-k-tuple-conjecture-form-and-what-we-should-proof

20 July, 2019 at 1:27 pm

Maths junior

Dear Prof. Tao,

I’m looking for a book that’s about (or at least contains a chapter on) the Cramér models. I’d be grateful for a suggestion.

W\BR

26 August, 2019 at 2:05 pm

Large prime gaps and probabilistic models | What's new

[…] more devoid of primes than average, and this region is not well explored by existing numerics. See this previous blog post for more discussion of Granville’s […]

17 December, 2019 at 8:27 am

254A, Notes 10 – mean values of nonpretentious multiplicative functions | What's new

[…] following from Exercise 33 of Notes 2). On the other hand, the randomness heuristics from Supplement 4 suggest that should be able to be taken as small as , and perhaps even if one is particularly […]

30 June, 2020 at 12:35 pm

Heath-Brown’s theorem on prime twins and Siegel zeroes | What's new

[…] problem is discussed in these previous blog posts; this obstruction is ultimately powered by the Möbius pseudorandomness principle that asserts that the Möbius function is asymptotically orthogonal to all […]

9 October, 2021 at 10:57 pm

N is a number

Just a small typo: in line 2 under the section title “The Cramer random model”, I think the name of the mathematician should be Harald Cramer.

[Corrected, thanks – T.]

10 November, 2021 at 3:48 am

Aditya Guha Roy

Reblogged this on Aditya Guha Roy's weblog.

23 July, 2022 at 8:52 am

Chowla’s conjecture and the Riemann hypothesis via the Liouville function | I Can't Believe It's Not Random!

[…] of these notes by Soundararajan. Several other ways to leverage this heuristic are presented in this blog post of […]

2 October, 2023 at 8:38 am

If there is no reason for structure, assume there is none. – Vasek Rozhon's blog

[…] model of primes has a name – Cramér’s random model. The Riemann hypothesis is equivalent to the claim that the prime number theorem is never wrong by […]

26 October, 2023 at 4:22 pm

Anonymous

There is a typo. In the sentence that starts with “Writing 1 – 2/p as… the term should be (1-1/p)^2 and not (1 – 2/p)^2 as stated.

[Corrected, thanks -T.]

13 December, 2023 at 4:52 am

Anonymous

Dear Tao, reading this post came to my mind the “Active inference” methods by Carl Friston and team where they build a network of prob. distribution (of different families) connected by transformation functions, like non-linearities in ANN, that then they update (their params) to fit the data they are exposed to, so the “prior”, the network of distributions, converges to the real distribution like in Bayes inference.

My take is, a modified version of it (maybe you need to add a new family of transformation like 1/log(n)) could be used to build a “distribution of primes” or alike, let say by exposing it to the 10, 100, 1000, etc. primes, and trying to find where the succesion of distributions obtained converges or not. If it does, then you end up having a “data-driven” distribution similar to the ones comented above.

99% it is BS, but who knows!
Sergio Hernandez.

13 December, 2023 at 4:53 am

Anonymous

Paper on those techniques: https://www.sciencedirect.com/science/article/pii/S0022249620300857

A proposed challenge to find such distributions: https://www.lesswrong.com/posts/uH4GfZwBYteiy2GrL/revisiting-the-manifold-hypothesis

5 April, 2024 at 9:41 am

Anonymous

Dear professor Tao: In the proof of Prediction 8, should the claim that $X_n$ is independent of $X_m$ unless $|n - m| \leq 2$ be that unless $|X_n - X_m| = 2$ instead? And why the required bound then follows from Chebyshev? Thank you.

[I believe the statement is correct as written. Note that $X_n$ depends only on the events $n \in {\mathcal P}$ , $n+2 \in {\mathcal P}$ , and similarly for $X_m$ . -T]

23 April, 2024 at 11:25 am

Anonymous

Dear professor Tao:

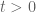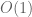For the last proof of Prediction 3, with the given bound, a direct application of Chebyshev’s inequality gives ${\bf P}(|\sum_{2 < n \leq x} X_n - O(x^{1/2 + o(1)})| \geq t) \leq \frac{O(x^{1+o(1)})}{t^2}$ for some threshold $t > 0$ . I wonder what value of $t$ is being inserted here and if the $O(1)$ term gets absorbed into $O(x^{1/2 + \varepsilon})$ in the end?

23 April, 2024 at 6:21 pm

Terence Tao

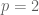Here we are using Chebyshev’s inequality in what is called the “measure-theoretic” form in https://en.wikipedia.org/wiki/Chebyshev%27s_inequality#Measure-theoretic_statement in order to get more decay in the $t$ parameter (by taking the “ $p$ ” parameter to be large, here we call it $k$ ); the $p=2$ case of Chebyshev’s inequality is too weak for this application.

	Anonymous on Erratum for “An inverse…
	Anonymous on Infinite partial sumsets in th…
	Anonymous on Infinite partial sumsets in th…
	Anonymous on A Banach algebra proof of the…
	Anonymous on A Banach algebra proof of the…
	Aleksandar on 245C, Notes 4: Sobolev sp…
	Anonymous on Erratum for “An inverse…
	Anonymous on Erratum for “An inverse…
	Anonymous on Erratum for “An inverse…
	Anonymous on Erratum for “An inverse…
	Terence Tao on 245C, Notes 4: Sobolev sp…
	Terence Tao on 275A, Notes 3: The weak and st…
	Terence Tao on What is a gauge?
	Terence Tao on Erratum for “An inverse…
	Terence Tao on 275A, Notes 3: The weak and st…

254A, Supplement 4: Probabilistic models and heuristics for the primes (optional)

Recent Comments

Articles by others

Diversions

Mathematics

Selected articles

Software

The sciences

Top Posts

Archives

Categories

The Polymath Blog

79 comments

Leave a comment Cancel reply

For commenters

254A, Supplement 4: Probabilistic models and heuristics for the primes (optional)

Share this:

Recent Comments

Articles by others

Diversions

Mathematics

Selected articles

Software

The sciences

Top Posts

Archives

Categories

The Polymath Blog

79 comments

Leave a comment Cancel reply

For commenters