The determinant of an
matrix (with coefficients in an arbitrary field) obey many useful identities, starting of course with the fundamental multiplicativity
for
matrices
. This multiplicativity can in turn be used to establish many further identities; in particular, as shown in this previous post, it implies the Schur determinant identity
whenever is an invertible
matrix,
is an
matrix,
is a
matrix, and
is a
matrix. The matrix
is known as the Schur complement of the block
.
I only recently discovered that this identity in turn immediately implies what I always found to be a somewhat curious identity, namely the Dodgson condensation identity (also known as the Desnanot-Jacobi identity)
for any and
matrix
, where
denotes the
matrix formed from
by removing the
row and
column, and similarly
denotes the
matrix formed from
by removing the
and
rows and
and
columns. Thus for instance when
we obtain
for any scalars . (Charles Dodgson, better known by his pen name Lewis Caroll, is of course also known for writing “Alice in Wonderland” and “Through the Looking Glass“.)
The derivation is not new; it is for instance noted explicitly in this paper of Brualdi and Schneider, though I do not know if this is the earliest place in the literature where it can be found. (EDIT: Apoorva Khare has pointed out to me that the original arguments of Dodgson can be interpreted as implicitly following this derivation.) I thought it is worth presenting the short derivation here, though.
Firstly, by swapping the first and rows, and similarly for the columns, it is easy to see that the Dodgson condensation identity is equivalent to the variant
Now write
where is an
matrix,
are
column vectors,
are
row vectors, and
are scalars. If
is invertible, we may apply the Schur determinant identity repeatedly to conclude that
and the claim (2) then follows by a brief calculation (and the explicit form of the
determinant). To remove the requirement that
be invertible, one can use a limiting argument, noting that one can work without loss of generality in an algebraically closed field, and in such a field, the set of invertible matrices is dense in the Zariski topology. (In the case when the scalars are reals or complexes, one can just use density in the ordinary topology instead if desired.)
The same argument gives the more general determinant identity of Sylvester
whenever ,
is a
-element subset of
, and
denotes the matrix formed from
by removing the rows associated to
and the columns associated to
. (The Dodgson condensation identity is basically the
case of this identity.)
A closely related proof of (2) proceeds by elementary row and column operations. Observe that if one adds some multiple of one of the first rows of
to one of the last two rows of
, then the left and right sides of (2) do not change. If the minor
is invertible, this allows one to reduce to the case where the components
of the matrix vanish. Similarly, using elementary column operations instead of row operations we may assume that
vanish. All matrices involved are now block-diagonal and the identity follows from a routine computation.
The latter approach can also prove the cute identity
for any , any
column vectors
, and any
matrix
, which can for instance be found in page 7 of this text of Karlin. Observe that both sides of this identity are unchanged if one adds some multiple of any column of
to one of
; for generic
, this allows one to reduce
to have only the first two entries allowed to be non-zero, at which point the determinants split into
and
determinants and we can reduce to the
case (eliminating the role of
). One can now either proceed by a direct computation, or by observing that the left-hand side is quartilinear in
and antisymmetric in
and
which forces it to be a scalar multiple of
, at which point one can test the identity at a single point (e.g.
and
for the standard basis
) to conclude the argument. (One can also derive this identity from the Sylvester determinant identity but I think the calculations are a little messier if one goes by that route. Conversely, one can recover the Dodgson condensation identity from Karlin’s identity by setting
,
(for instance) and then permuting some rows and columns.)

13 comments
Comments feed for this article
28 August, 2017 at 4:01 pm
André Camargo
Schur complements are closely related to the Gaussian block elimination strategy
where we use the block to produce all the zeros below it. It might be interesting to notice that
to produce all the zeros below it. It might be interesting to notice that
one can produce these zeros through thousands of other manners and, for each elimination strategy we choose,
a different determinantal identity of Sylvester type can be established. This fact was noticed by Mühlbach
http://www.sciencedirect.com/science/article/pii/002437959090060P.
Sylvester’s identity can also be interpreted as follows: first we take the Leibniz’ formula for the determinant of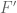
and then we use that, by the Schur determinantal identity, each entry of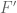 is a ratio of the minors of
is a ratio of the minors of  .
.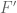 (Laplace expansions, for instance), we obtain, after replacements through the Schur determinantal identity, another identity on minors of
(Laplace expansions, for instance), we obtain, after replacements through the Schur determinantal identity, another identity on minors of  . This general principle is known as Muir’s law of extensible minors and it is proved through Schur complements in the paper of Brualdi and Schneider. This principle was established By Muir in 1881, but curiously, Muir did not use Gaussian elimination explicitly. Using other elimination estrategies than the Gaussian one, Mühlbach generalized Muir’s law.
. This general principle is known as Muir’s law of extensible minors and it is proved through Schur complements in the paper of Brualdi and Schneider. This principle was established By Muir in 1881, but curiously, Muir did not use Gaussian elimination explicitly. Using other elimination estrategies than the Gaussian one, Mühlbach generalized Muir’s law.
After these replacements, we get Sylvester’s identity. If we apply this same procedure to other algebraic relation between the minors of
10 September, 2017 at 1:03 pm
aquazorcarson
Here is another interesting matrix identity that can be derived from Schur’s complement formula: https://mathoverflow.net/questions/87877/jacobis-equality-between-complementary-minors-of-inverse-matrices
11 September, 2017 at 11:06 am
André Camargo
Indeed. Brualdi and Schneider prove Jacobi’s identity in their paper through Schur complements. It can be also derived directly from Sylvester’s identity (see my post below).
29 August, 2017 at 5:56 am
John Mangual
I have always wondered what our fixation with determinants are. Matrix multiplication is just a short-hand doing one linear substitution and then another. If we have another algebra, the multiplication might look a little bit different.
29 August, 2017 at 7:28 am
Terence Tao
If you do discover another algebra that has a comparable utility and richness as linear algebra, please do let the rest of us know. In the meantime, you might take a look at the answers to this question: https://mathoverflow.net/questions/35988/why-were-matrix-determinants-once-such-a-big-deal
EDIT: There are interesting variants of the determinant, such as the Pfaffian, the permanent, the tropical determinant, or immanants, which may be thought of as arising from slightly different algebraic foundations than classical linear algebra (e.g. supercommutative algebra, tropical algebra, etc.). However, these variants, as fascinating as they are, are not nearly as broadly useful to modern mathematics as the classical determinant.
18 September, 2017 at 4:13 pm
John Darius Mangual
DAHA
29 August, 2017 at 4:37 pm
Darij Grinberg
If you allow the Zariski density argument (a.k.a. Weyl’s principle of irrelevance of algebraic inequalities) to assume that certain matrices are invertible, then a lot of identities like this boil down to each other. If one forbids this argument, however, the situation changes (similar to how trivially equivalent combinatorial identities can turn into completely different problems when one asks for a bijective proof). The Sylvester identity has been combinatorially proven by Berliner and Brualdi ( http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.531.364 ); the particular case that is Dodgson condensation has been done by Zeilberger earlier ( https://arxiv.org/abs/math/9808079v1 ). There are other identities where such a proof remains to be found; to my knowledge, det (adj A) = (det A)^{n-1} is one of those.
Note that your proof of the “cute identity” can be made even simpler: Any row operations preserve the identity, as long as they are performed simultaneously on X_1, X_2, Y_1, Y_2 and A. Thus, we can in particular transform (X_1, X_2, A) into the identity matrix, so the only freedom remains in the vectors Y_1 and Y_2. This is spelt out in the proof of Lemma 14.2 in http://arxiv.org/abs/1402.6178v6 (a 134-page paper which, in a sense, is built upon this “cute identity”).
30 August, 2017 at 7:25 pm
André Camargo
Indeed, I have been study some of these determinantal identities for a while and it turns out that many of them are equivalent to each other. For instance, the identity for the determinant of the Adjugate for a matrix of
of follows directly from Sylvester’s identity applied to the matrix
follows directly from Sylvester’s identity applied to the matrix 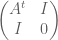 of size
of size 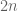 (I = identity matrix). A similar reasoning shows that Sylvester’s identity is actually algebraically equivalent to Jacobi’s identity, which expresses any minor of the Adjugate in terms of the minors of
(I = identity matrix). A similar reasoning shows that Sylvester’s identity is actually algebraically equivalent to Jacobi’s identity, which expresses any minor of the Adjugate in terms of the minors of  (the details can be found here http://www.sciencedirect.com/science/article/pii/S0024379515003092.)
(the details can be found here http://www.sciencedirect.com/science/article/pii/S0024379515003092.)
size
Actually MANY MANY determinantal identities for a matrix $A$ can be obtained through some other determinantal identity for a matrix which contains $A$ as a submatrix. In fact, Leclerc showed that most of the known determinantal identities are particular cases of an identity of Turnbull of 1909 (see the details here http://www.sciencedirect.com/science/article/pii/S0001870883710303). Leclerc interpreted Turnbull’s identity as the
associativity and anticommutativity of the second product of Peano/Cayley Algebras, but, in essence, it just compares some iterative Laplace expansions of a same determinant before and after some elimination process is performed. However, although powerful, Turnbull’s identity may not be intuitive. For instance, an example of obtaining Sylvester’s identity from Turnbull’s identity is given in Section 5 of http://www.tandfonline.com/doi/abs/10.1080/03081087.2012.740028.
Just to finish: the following paper http://www.combinatorics.org/ojs/index.php/eljc/article/view/v19i3p21/pdf proves several determinantal identities bijectively, including Turnbull’s one. Thus, using Leclerc’s approach, it turns out that bijective proofs exist for most of the known determinantal identities.
3 September, 2017 at 2:19 pm
Darij Grinberg
I wasn’t aware of the fact that the det (adj A) = (det A)^{n-1} formula is a particular case of the Dodgson-Muir identity. Since the latter is proven bijectively in the Berliner-Brualdi paper, this settles the question for a bijective proof of the former. Thank you!
You have answered a long-standing MO and m.se question with this, by the way… if only I could find it.
31 August, 2017 at 1:35 am
Rajesh
Prof Tao :
Can you attempt this open problem of finding an almost closed form expression or if not expression but some insight into properties of first eigenfunction of p=3-Laplacian of a square domain in R^2 under periodic boundary conditions. (Some thing like the sin_p function in case of 1-D). I have computed the solution, but I need more insights than computation. Its simple structure suggest some insight may be gained into this function. Its been a long standing open problem and appreciate your insights suggestions and efforts.
https://mathoverflow.net/q/279771/14414
Regards
Rajesh
1 September, 2017 at 7:13 pm
Rajesh
I think I have just solved this problem. Request you to please have a look at the answer to that question. Appreciate your comments.
Regards
Rajesh
30 September, 2017 at 9:38 am
An update to “On the sign patterns of entrywise positivity preservers in fixed dimension” | What's new
[…] proven relatively easy by an induction argument, relying on the Dodgson and Karlin identities from this previous post; the difficulties are largely notational in nature. Combining this result with the Jacobi-Trudi […]
11 June, 2018 at 3:29 am
John Mangual
One geometrically intuitive way of looking at the determinant is as the volume of a box.
At some point, we learned to express this volume as the wedge product of three vectors. Let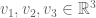 we have the determinant formula:
we have the determinant formula: 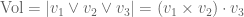 .
.
Even our definition of cross product is a highly remarkable thing, as the matrix entries are also vectors.