Kevin Ford, Sergei Konyagin, James Maynard, Carl Pomerance, and I have uploaded to the arXiv our paper “Long gaps in sieved sets“, submitted to J. Europ. Math. Soc..
This paper originated from the MSRI program in analytic number theory last year, and was centred around variants of the question of finding large gaps between primes. As discussed for instance in this previous post, it is now known that within the set of primes , one can find infinitely many adjacent elements
whose gap
obeys a lower bound of the form
where denotes the
-fold iterated logarithm. This compares with the trivial bound of
that one can obtain from the prime number theorem and the pigeonhole principle. Several years ago, Pomerance posed the question of whether analogous improvements to the trivial bound can be obtained for such sets as
Here there is the obvious initial issue that this set is not even known to be infinite (this is the fourth Landau problem), but let us assume for the sake of discussion that this set is indeed infinite, so that we have an infinite number of gaps to speak of. Standard sieve theory techniques give upper bounds for the density of that is comparable (up to an absolute constant) to the prime number theorem bounds for
, so again we can obtain a trivial bound of
for the gaps of
. In this paper we improve this to
for an absolute constant ; this is not as strong as the corresponding bound for
, but still improves over the trivial bound. In fact we can handle more general “sifted sets” than just
. Recall from the sieve of Eratosthenes that the elements of
in, say, the interval
can be obtained by removing from
one residue class modulo
for each prime up to
, namely the class
mod
. In a similar vein, the elements of
in
can be obtained by removing for each prime
up to
zero, one, or two residue classes modulo
, depending on whether
is a quadratic residue modulo
. On the average, one residue class will be removed (this is a very basic case of the Chebotarev density theorem), so this sieving system is “one-dimensional on the average”. Roughly speaking, our arguments apply to any other set of numbers arising from a sieving system that is one-dimensional on average. (One can consider other dimensions also, but unfortunately our methods seem to give results that are worse than a trivial bound when the dimension is less than or greater than one.)
The standard “Erdős-Rankin” method for constructing long gaps between primes proceeds by trying to line up some residue classes modulo small primes so that they collectively occupy a long interval. A key tool in doing so are the smooth number estimates of de Bruijn and others, which among other things assert that if one removes from an interval such as
all the residue classes
mod
for
between
and
for some fixed
, then the set of survivors has exceptionally small density (roughly of the order of
, with the precise density given by the Dickman function), in marked contrast to the situation in which one randomly removes one residue class for each such prime
, in which the density is more like
. One generally exploits this phenomenon to sieve out almost all the elements of a long interval using some of the primes available, and then using the remaining primes to cover up the remaining elements that have not already been sifted out. In the more recent work on this problem, advanced combinatorial tools such as hypergraph covering lemmas are used for the latter task.
In the case of , there does not appear to be any analogue of smooth numbers, in the sense that there is no obvious way to arrange the residue classes so that they have significantly fewer survivors than a random arrangement. Instead we adopt the following semi-random strategy to cover an interval
by residue classes. Firstly, we randomly remove residue classes for primes
up to some intermediate threshold
(smaller than
by a logarithmic factor), leaving behind a preliminary sifted set
. Then, for each prime
between
and another intermediate threshold
, we remove a residue class mod
that maximises (or nearly maximises) its intersection with
. This ends up reducing the number of survivors to be significantly below what one would achieve if one selects residue classes randomly, particularly if one also uses the hypergraph covering lemma from our previous paper. Finally, we cover each the remaining survivors by a residue class from a remaining available prime.

12 comments
Comments feed for this article
21 February, 2018 at 11:38 pm
Anonymous
Can this 2-steps removal strategy be generalized into 3-steps removal strategy (by introducing another intermediate threshold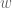 between
between  and
and  )?
)? whose number is not necessarily fixed, but may slowly increasing with
whose number is not necessarily fixed, but may slowly increasing with  ).
).
This seems to lead to a general multisteps removal strategy (based on increasing sequence of intermediate thresholds
22 February, 2018 at 8:24 am
Terence Tao
Our initial selection strategy was indeed of this form, but we realised later that it was unnecessarily complicated, and that a two-step procedure actually gave comparable bounds. (Strictly speaking it is a three-step process, there is a standard “final cleanup” phase in which one uses the primes between to
to  to eliminate the few elements that survive all the previous sieving steps, but nothing particularly interesting or innovative happens in this final phase.)
to eliminate the few elements that survive all the previous sieving steps, but nothing particularly interesting or innovative happens in this final phase.)
22 February, 2018 at 2:16 pm
arch1
infinitely adjacent -> infinitely many adjacent [??]
[Corrected, thanks – T.]
23 February, 2018 at 4:49 pm
Anonymous
Conjecture: For any positive integer, n ≥ 2, there are at least two prime numbers between n^2 and (n+1)^2.
We can show that
π( (n+1)^2 ) – π (n^2 ) > π (.5*n ) ≥ 2 when n≥ 6.
Here’s a proof:
According to the Prime Number Theorem, we have
π( (n+1)^2 ) = (n+1)^2/log((n+1)^2) +/- error;
π( n^2 ) = n^2/log(n^2) +/- error;
π( .5×n ) = .5×n/log(.5×n) +/- error
= .5×n/log(n) +/- error
Therefore,
π( (n+1)^2 ) – π( n^2 ) = 2n/log(n^2) +/-error = n/log(n) +/- error.
Hence, π( (n+1)^2 ) – π( n^2 ) > π( .5×n ).
Thus, for n≥ 6 the conjecture is affirmed.
Moreover, the conjecture is easily affirmed for n≥2.
https://www.quora.com/Can-we-disprove-that-for-any-positive-integer-n-there-are-at-least-two-prime-numbers-between-n-2-and-n-1-2/answer/David-Cole-146
24 February, 2018 at 12:04 am
Anonymous
Landau’s Fourth Problem: Are there infinitely many primes of the form, (2n)^2+1, where n is a positive integer?
The answer for Landau’s Fourth Problem is affirmative!
Relevant Reference Link:
24 February, 2018 at 6:53 am
K
May I ask a non-mathematician question: How does a mathematician collaboration work when then collaborators are not at the same university? I imagine it quite difficult sharing ideas between 5 people just via e-mail and sometimes via skype meeting? In contrast to other areas of science, I imagine that in mathematics discussions about the ideas are more difficult (which is why in average math papers there are less authors than on physics papers). Do you also use (hidden) wordpress discussions as for the polymath projects? (Maybe your answer could give some hints for improving the efficiency of my collaborations)
24 February, 2018 at 8:12 am
Terence Tao
Well in this case, the four of us were physically present together at the MSRI program, so we definitely met face to face for core of the project. But then the writing up process was done almost entirely by email. More generally, I think collaborations in mathematics nowadays typically involve a short period of meeting physically (for say a week) to try to work on the core aspect of the problem (e.g. solving what one believes to be the most difficult step or most crucial case) and then working everything else out online using more or less off-the-shelf tools (email, Skype, dropbox, subversion, git, etc..). In a few cases I have also used private blogs, wikis, discussion groups, and even at one point a Facebook page.
25 February, 2018 at 8:40 am
Anonymous
In your set, P_2, have you considered the possibility, b – a ≥ 2a, for infinitely many adjacent elements of that set?
25 February, 2018 at 11:54 am
Terence Tao
In that case the theorem is trivially true (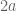 is much larger than
is much larger than  for large
for large  ).
).
25 February, 2018 at 1:13 pm
Anonymous
Yes! You’re correct. But a gap of size 2a for b – a is much too big. There are primes galore in such gaps between adjacent elements, a and b, if they exist in P_2. I believe max(b – a) = Ω × a where 0 < Ω < 0.2 (or much less for large a).
26 February, 2018 at 9:26 am
Anonymous
For large a, the parameter, Ω, is constrained according to the distribution of primes or according to the great Prime Number Theorem (PNT).
11 November, 2018 at 1:21 am
John Cureg Saccuan
Title: DNA Of Prime Numbers & Saccuan’s Factorization Method
Noted:
Saccuan’s factorization method (Improvement of Quadratic sieve and application of Legendre’s conjecture)
P=w^2+m
P=pq
p=GCD[P,x^2+m] or q=GCD[P,x^2+m]
Where:
w=Floor[P^.5]
m=P-w^2 or Mod(P,w^2)
Range: x={0,1…w or 4*w}
Overview:
Theorem:
There are many infinite natural Integers in the form of P=w^2+m
Legendre’s conjecture:
Does there always exist at least one prime between consecutive perfect squares?
w^2 (w+1)^2
Counterexample:
16=4^2+0
17=4^2+1(Prime)
18=4^2+2
19=4^2+3
20=4^2+4
21=4^2+5
22=4^2+6
23=4^2+7(Prime)
24=4^2+8
25=(4+1)^2+0
Saccuan’s factorization method
Example:
P=21 then w=4 and m=5
x=0;GCD[21,0^2+5]=1
x=1;GCD[21,1^2+5]=3
x=2;GCD[21,2^2+5]=3
x=3;GCD[21,3^2+5]=7
x=4;GCD[21,4^2+5]=21
x=5;GCD[21,5^2+5]=3
x=6;GCD[21,6^2+5]=1
x=7;GCD[21,7^2+5]=3
x=8;GCD[21,8^2+5]=3
*
*
*
*
x=infinity
https://www.dropbox.com/sh/shq0l3eg42rfy9h/AAC7SetZQPY68GUYriLql4Gua?dl=0
Objective:Please help me to proof that I’m correct in my method. I want to add this in Wikipedia, new type of factoring algorithms at Integer factorization section. but i need first to verify by other mathematician.