Joni Teräväinen and I have just uploaded to the arXiv our paper “The structure of correlations of multiplicative functions at almost all scales, with applications to the Chowla and Elliott conjectures“. This is a sequel to our previous paper that studied logarithmic correlations of the form
where were bounded multiplicative functions,
were fixed shifts,
was a quantity going off to infinity, and
was a generalised limit functional. Our main technical result asserted that these correlations were necessarily the uniform limit of periodic functions
. Furthermore, if
(weakly) pretended to be a Dirichlet character
, then the
could be chosen to be
–isotypic in the sense that
whenever
are integers with
coprime to the periods of
and
; otherwise, if
did not weakly pretend to be any Dirichlet character
, then
vanished completely. This was then used to verify several cases of the logarithmically averaged Elliott and Chowla conjectures.
The purpose of this paper was to investigate the extent to which the methods could be extended to non-logarithmically averaged settings. For our main technical result, we now considered the unweighted averages
where is an additional parameter. Our main result was now as follows. If
did not weakly pretend to be a twisted Dirichlet character
, then
converged to zero on (doubly logarithmic) average as
. If instead
did pretend to be such a twisted Dirichlet character, then
converged on (doubly logarithmic) average to a limit
of
-isotypic functions
. Thus, roughly speaking, one has the approximation
for most .
Informally, this says that at almost all scales (where “almost all” means “outside of a set of logarithmic density zero”), the non-logarithmic averages behave much like their logarithmic counterparts except for a possible additional twisting by an Archimedean character
(which interacts with the Archimedean parameter
in much the same way that the Dirichlet character
interacts with the non-Archimedean parameter
). One consequence of this is that most of the recent results on the logarithmically averaged Chowla and Elliott conjectures can now be extended to their non-logarithmically averaged counterparts, so long as one excludes a set of exceptional scales
of logarithmic density zero. For instance, the Chowla conjecture
is now established for either odd or equal to
, so long as one excludes an exceptional set of scales.
In the logarithmically averaged setup, the main idea was to combine two very different pieces of information on . The first, coming from recent results in ergodic theory, was to show that
was well approximated in some sense by a nilsequence. The second was to use the “entropy decrement argument” to obtain an approximate isotopy property of the form
for “most” primes and integers
. Combining the two facts, one eventually finds that only the almost periodic components of the nilsequence are relevant.
In the current situation, each is approximated by a nilsequence, but the nilsequence can vary with
(although there is some useful “Lipschitz continuity” of this nilsequence with respect to the
parameter). Meanwhile, the entropy decrement argument gives an approximation basically of the form
for “most” . The arguments then proceed largely as in the logarithmically averaged case. A key lemma to handle the dependence on the new parameter
is the following cohomological statement: if one has a map
that was a quasimorphism in the sense that
for all
and some small
, then there exists a real number
such that
for all small
. This is achieved by applying a standard “cocycle averaging argument” to the cocycle
.
It would of course be desirable to not have the set of exceptional scales. We only know of one (implausible) scenario in which we can do this, namely when one has far fewer (in particular, subexponentially many) sign patterns for (say) the Liouville function than predicted by the Chowla conjecture. In this scenario (roughly analogous to the “Siegel zero” scenario in multiplicative number theory), the entropy of the Liouville sign patterns is so small that the entropy decrement argument becomes powerful enough to control all scales rather than almost all scales. On the other hand, this scenario seems to be self-defeating, in that it allows one to establish a large number of cases of the Chowla conjecture, and the full Chowla conjecture is inconsistent with having unusually few sign patterns. Still it hints that future work in this direction may need to split into “low entropy” and “high entropy” cases, in analogy to how many arguments in multiplicative number theory have to split into the “Siegel zero” and “no Siegel zero” cases.

8 comments
Comments feed for this article
10 September, 2018 at 3:34 pm
Anonymous
Are these methods sufficient to improve the current upper bounds on the growth rate of summatory functions (i.e. partial sums) for certain multiplicative functions with “small corelation” in some quantitative sense ?
11 September, 2018 at 8:41 am
Terence Tao
The methods here give quite small gains over the trivial bound (the gain tends to be something like a small power of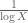 at best). So direct estimation of summatory functions (e.g., using Halasz’s theorem) will likely give significantly stronger bounds. The tools used in this sort of work (ergodic theory, entropy decrement, and the Matomaki-Radziwill theorem) are probably best thought of as tools to improve
at best). So direct estimation of summatory functions (e.g., using Halasz’s theorem) will likely give significantly stronger bounds. The tools used in this sort of work (ergodic theory, entropy decrement, and the Matomaki-Radziwill theorem) are probably best thought of as tools to improve 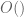 type trivial bounds to
type trivial bounds to  bounds, but without really strong decay rates.
bounds, but without really strong decay rates.
17 December, 2023 at 6:17 am
Xu
Why can’t we apply the entropy decrement method repeatedly: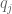
 of primes of magnitude
of primes of magnitude 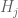 ,
, we have
we have  ,
,
 and for all
and for all  we have
we have
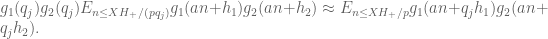
First, we construct the sequence of primes
and sets
such that for all
Next, use the entropy decrement method to prove the existence of such that for all
such that for all  we have
we have
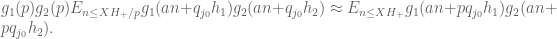
 to get the non-logarithmically averaged result?
to get the non-logarithmically averaged result?
Finally, apply the circle method to the latter average summed over
20 December, 2023 at 10:44 am
Terence Tao
This type of approach will allow one to control a lot of scales (those scales that are comparable to for enough “good” primes
for enough “good” primes  ) but it does not seem strong enough to control *all* scales, due to inability to rule out the possibility that there are some scales
) but it does not seem strong enough to control *all* scales, due to inability to rule out the possibility that there are some scales  that contain very few good primes.
that contain very few good primes.
22 December, 2023 at 11:29 pm
Xu
Quotation: " … we construct the sequence of primes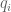
 of primes of magnitude
of primes of magnitude  ,
, we have
we have  ,
,
 and
and
![\displaystyle E_{n\le Xpq_i} \sum_{p \in P(H_i)} \sum_{j: j,j+pq_ih \in [1,H_{+}]} \overline{g_1}(p)\overline{g_2}(p) 1_{an+j = pq_ib \ (apq_i)} g_1(an+j) g_2(an+j+pq_ih) \approx \frac{1}{q_i} E_{n\le Xpq_i} \sum_{p \in P(H_i)} \sum_{j: j,j+pq_ih \in [1,H_{+}]} \overline{g_1}(p)\overline{g_2}(p) 1_{an+j = pb \ (ap)} g_1(an+j) g_2(an+j+pq_ih).](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+E_%7Bn%5Cle+Xpq_i%7D+%5Csum_%7Bp+%5Cin+P%28H_i%29%7D+%5Csum_%7Bj%3A+j%2Cj%2Bpq_ih+%5Cin+%5B1%2CH_%7B%2B%7D%5D%7D+%5Coverline%7Bg_1%7D%28p%29%5Coverline%7Bg_2%7D%28p%29+1_%7Ban%2Bj+%3D+pq_ib+%5C+%28apq_i%29%7D+g_1%28an%2Bj%29+g_2%28an%2Bj%2Bpq_ih%29+%5Capprox+%5Cfrac%7B1%7D%7Bq_i%7D+E_%7Bn%5Cle+Xpq_i%7D+%5Csum_%7Bp+%5Cin+P%28H_i%29%7D+%5Csum_%7Bj%3A+j%2Cj%2Bpq_ih+%5Cin+%5B1%2CH_%7B%2B%7D%5D%7D+%5Coverline%7Bg_1%7D%28p%29%5Coverline%7Bg_2%7D%28p%29+1_%7Ban%2Bj+%3D+pb+%5C+%28ap%29%7D+g_1%28an%2Bj%29+g_2%28an%2Bj%2Bpq_ih%29.&bg=ffffff&fg=545454&s=0&c=20201002)
and sets
such that for all
A value of the latter expression is almost unchanged when one replaces with
with  and
and  with
with  , where
, where  is a permutation on
is a permutation on  , preserving the residue classes
, preserving the residue classes  .
. for which one can approximate the latter expression by
for which one can approximate the latter expression by
![\displaystyle E_{n\le Xpq_i} \sum_{p \in P(H_i)} \sum_{j: j,j+pq_ih \in [1,H_{+}]} \overline{g_1}(p)\overline{g_2}(p) 1_{an+j = 0 \ (q_i)} 1_{an+j = pb \ (ap)} g_1(\sigma(an+j)) g_2(\sigma(an+j+pq_ih))](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+E_%7Bn%5Cle+Xpq_i%7D+%5Csum_%7Bp+%5Cin+P%28H_i%29%7D+%5Csum_%7Bj%3A+j%2Cj%2Bpq_ih+%5Cin+%5B1%2CH_%7B%2B%7D%5D%7D+%5Coverline%7Bg_1%7D%28p%29%5Coverline%7Bg_2%7D%28p%29+1_%7Ban%2Bj+%3D+0+%5C+%28q_i%29%7D+1_%7Ban%2Bj+%3D+pb+%5C+%28ap%29%7D+g_1%28%5Csigma%28an%2Bj%29%29+g_2%28%5Csigma%28an%2Bj%2Bpq_ih%29%29&bg=ffffff&fg=545454&s=0&c=20201002)
Thus there exists a
and apply the entropy decrement method to the random tuple , being the consecutive nonzero elements of the sparse random tuple
, being the consecutive nonzero elements of the sparse random tuple  ,
,  , (extended to
, (extended to  periodically).
periodically).
 "
"
We note that the following bound on the entropy holds:
11 September, 2018 at 1:49 pm
Ibrahim
please sir, I m a graduate trying to proposed a theory on integers, would you please help me with my theory my email address is ibmuhd557@gmail.com.
Waiting for your reply thank you sir.
13 October, 2018 at 8:47 pm
think
Google on “cocycle averaging argument” only points here and so unsure if it is standard. Is it used anywhere else? How is “siegel zero” presence analogous to the “low entropy” case? ‘Low entropy’ should roughly mean properties about primes are ‘predictable’ in some sense.
31 October, 2018 at 10:31 pm
YNWA
Dear all, you might be interested in this question concerning the Riemann zeta function on MathOverflow: https://mathoverflow.net/q/314310/130815