(This post is mostly intended for my own reference, as I found myself repeatedly looking up several conversions between polynomial bases on various occasions.)
Let denote the vector space of polynomials
of one variable
with real coefficients of degree at most
. This is a vector space of dimension
, and the sequence of these spaces form a filtration:
A standard basis for these vector spaces are given by the monomials : every polynomial
in
can be expressed uniquely as a linear combination of the first
monomials
. More generally, if one has any sequence
of polynomials, with each
of degree exactly
, then an easy induction shows that
forms a basis for
.
In particular, if we have two such sequences and
of polynomials, with each
of degree
and each
of degree
, then
must be expressible uniquely as a linear combination of the polynomials
, thus we have an identity of the form
for some change of basis coefficients . These coefficients describe how to convert a polynomial expressed in the
basis into a polynomial expressed in the
basis.
Many standard combinatorial quantities involving two natural numbers
can be interpreted as such change of basis coefficients. The most familiar example are the binomial coefficients
, which measures the conversion from the shifted monomial basis
to the monomial basis
, thanks to (a special case of) the binomial formula:
thus for instance
More generally, for any shift , the conversion from
to
is measured by the coefficients
, thanks to the general case of the binomial formula.
But there are other bases of interest too. For instance if one uses the falling factorial basis
then the conversion from falling factorials to monomials is given by the Stirling numbers of the first kind :
thus for instance
and the conversion back is given by the Stirling numbers of the second kind :
thus for instance
If one uses the binomial functions as a basis instead of the falling factorials, one of course can rewrite these conversions as
and
thus for instance
and
As a slight variant, if one instead uses rising factorials
then the conversion to monomials yields the unsigned Stirling numbers of the first kind:
thus for instance
One final basis comes from the polylogarithm functions
For instance one has
and more generally one has
for all natural numbers and some polynomial
of degree
(the Eulerian polynomials), which when converted to the monomial basis yields the (shifted) Eulerian numbers
For instance
These particular coefficients also have useful combinatorial interpretations. For instance:
- The binomial coefficient
is of course the number of
-element subsets of
.
- The unsigned Stirling numbers
of the first kind are the number of permutations of
with exactly
cycles. The signed Stirling numbers
are then given by the formula
.
- The Stirling numbers
of the second kind are the number of ways to partition
into
non-empty subsets.
- The Eulerian numbers
are the number of permutations of
with exactly
ascents.
These coefficients behave similarly to each other in several ways. For instance, the binomial coefficients obey the well known Pascal identity
(with the convention that vanishes outside of the range
). In a similar spirit, the unsigned Stirling numbers
of the first kind obey the identity
and the signed counterparts obey the identity
The Stirling numbers of the second kind obey the identity
and the Eulerian numbers obey the identity

24 comments
Comments feed for this article
7 April, 2019 at 8:27 am
Per Ekman
As someone that’s currently learning a bout the Binomial Theorem on my free time this couldn’t have been posted at a better time.
Thank you so much for sharing!
7 April, 2019 at 10:13 am
asahay22
Hmmm, do the basis change coefficients from the standard basis to an orthogonal basis relative to some integral inner product (e.g. Chebyshev polynomials) also have a combinatorial interpretation?
7 April, 2019 at 2:52 pm
Terence Tao
The basis change coefficients between the classical orthogonal polynomials and the monomial basis tend to be variants of binomial coefficients (for instance they often are expressible as ratios of products of factorials, times some other simple factors like powers of 2). For instance to convert monomials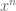 to Chebyshev polynomials
to Chebyshev polynomials  , one has the identity
, one has the identity  (with the convention that the binomial coefficient vanishes if the bottom argument is not an integer).
(with the convention that the binomial coefficient vanishes if the bottom argument is not an integer).
8 April, 2019 at 1:18 pm
Jake
See also things like Salzer’s method : https://dl.acm.org/citation.cfm?doid=355611.362548 and this chebfun discussion : http://www.chebfun.org/examples/cheb/FastChebyshevLegendreTransform.html
8 April, 2019 at 7:00 pm
Anonymous
The coefficients of (weighted) orthogonal polynomials expansion can also be evaluated by their corresponding (weighted) integral representation as inner products.
7 April, 2019 at 10:00 pm
Lou
Very nice. Any analogues for multivariate polynomials?
11 April, 2019 at 2:42 pm
Anonymous
See e.g. spherical harmonics (which are orthogonal polynomials on the unit sphere , or the more general
, or the more general  with respect to its Haar measure) with application to polynomial approximation on spheres.
with respect to its Haar measure) with application to polynomial approximation on spheres.
8 April, 2019 at 3:45 am
Pedro Sánchez Terraf
Dear Terry,
in the second line of the post you might like “…one variable x and of degree at most $n$”.
Best wishes!
[Corrected, thanks – T.]
8 April, 2019 at 11:55 am
greghighermathhelp
I was just learning about the calculus of finite differences last week, where the conversion of monomials into falling factorials allows for the evaluation of sums of kth powers, which I learned is a problem with a very long history. Now here it is again, with a nice connection to binomial coefficients and other combinatorial quantities! Thanks for fleshing this out.
9 April, 2019 at 1:03 am
Conversions between standard polynomial bases - Nevin Manimala's Blog
[…] by /u/HigherMathHelp [link] […]
9 April, 2019 at 3:26 am
LaurentC
There may lack a “minus” in your formula of $Li_1=-\long(1-x)$.
[Corrected, thanks – T.]
10 April, 2019 at 9:13 pm
Arch1
2nd paragraph of the post proper: “…can be expressed uniquely as *a linear combination of* the first n+1 monomials…”
[Corrected, thanks – T.]
11 April, 2019 at 7:17 am
Raymond E Rogers
You can systematize a lot of polynomial conversions and sequences by means of Sheffer generating functions and substituting an appropriate “creation” matrix for the indexing variable; giving a coefficient matrix. The Appell sequences are straightforward, and the generalized forms (Sheffer) require going through the matrix Jordan form.
11 April, 2019 at 12:58 pm
Rodolfo Niborski
Three formulas from the bottom :
“and the signed counterparts” instead of “unsigned”.
[Corrected, thanks – T.]
12 April, 2019 at 8:14 am
Ralph Burger
I once tried to find an explicit transformation for Fibonacci polynomials from to the
to the  basis, but failed to get a recursion free expression. Any ideas on that?
basis, but failed to get a recursion free expression. Any ideas on that?
12 April, 2019 at 9:24 am
Terence Tao
The first thing I would suggest is to compute the first few coefficients and enter that into the OEIS to see if you get a hit. (For instance, the Stirling numbers of the first kind appear as https://oeis.org/A008275 , the Stirling numbers of the second kind appear as https://oeis.org/A008277 , and the Eulerian numbers appear as https://oeis.org/A008292 .) If the sequence is not already in the OEIS, you can of course submit it in case some future researcher also stumbles upon it.
As an alternative to the OEIS one can also simply do a web search for some of the specific large numerical coefficients that you find. (For instance, if you pick a handful of large unsigned Stirling numbers of the first kind, such as 109584, 22449, and 13132, and do a web search, many of the hits will relate to the Stirling numbers.)
12 April, 2019 at 11:28 am
Raphael Berger
Thanks a lot for replying (my grandchildren will hear that)! OEIS is a great suggestion; I did it, just didn’t mention it, thought that won’t fit the small margin here (https://math.stackexchange.com/questions/2731420/variable-transformation-x-to-x1-in-fibonacci-polynomial-f-nx) ;-) So its not there, and afaiu 2D sequences are not really supported by OIES. (Since we already meet, I have a thought on the Töplitz conjecture, you don’t happen to have a post on it here?). All the best!! — Raphael B.
12 April, 2019 at 12:38 pm
Raymond E Rogers
I might not understand but the recursion in these cases (rational polynomial generating functions) is always the denominator applied to the series, with the numerator acting as startup/arbitrary constants.
12 April, 2019 at 2:26 pm
Ralph Burger
I do not understand exactly what you mean by apply, but as I wrote, the recursion is the easy bit, I aimed at the recursion-FREE expression (which might be a bad literal translation from the german “rekursionsfrei” and could be possibly paraphrased: “non-recursive”).
12 April, 2019 at 5:17 pm
Raymond E Rogers
As I read it, you want the closed form of the generating function? In that case, just substitute your x+1 into the generating function and do a partial fraction expansion on it. Then solve the first order terms in closed form. We should probably move this discussion out of this forum.
12 April, 2019 at 7:49 pm
Raymond Rogers
It occurs to me that you just want new coefficients? In an elementary form: just write out the polynomial as a coefficient array times a verticle base array; say (C_(x+1))*B1(X+1) Now expand (x+1)^n and you see it’s just a summation of binomial entries times X. Treat it as a convolution (or some such) and you see that you can convert the base to P()*B2(X) Where P() is the Pascal matrix with terms (n,k). Having rewritten it, you just use “associativity” and the new polynomial coefficients are C_x=C_(x+1)*P() and the new polynomial (actually the same one) reads C_x*B2(x). I hope this is closer to what you want.
13 April, 2019 at 12:20 am
Anonymous
Dear Raymond, thank you for your suggestion. My email is berger@chem.helsinki.fi. Maybe its better to continue
by email.
13 April, 2019 at 12:23 am
Anonymous
ps. in the link to math stack exchange you seeexactly how far i got. the problem is the secobd step after the binom. expansion to get back to fibonacci polynomials in x.
15 April, 2019 at 6:00 pm
JDM
I’m going to confess that I thought a lot of the discussion of Hilbert spaces of Lp spaces could be ameliorated if we use a basis of some kind. Has anyone in number theory computed a Gowers norm yet?