Let be some domain (such as the real numbers). For any natural number
, let
denote the space of symmetric real-valued functions
on
variables
, thus
for any permutation . For instance, for any natural numbers
, the elementary symmetric polynomials
will be an element of . With the pointwise product operation,
becomes a commutative real algebra. We include the case
, in which case
consists solely of the real constants.
Given two natural numbers , one can “lift” a symmetric function
of
variables to a symmetric function
of
variables by the formula
where ranges over all injections from
to
(the latter formula making it clearer that
is symmetric). Thus for instance
and
Also we have
With these conventions, we see that vanishes for
, and is equal to
if
. We also have the transitivity
if .
The lifting map is a linear map from
to
, but it is not a ring homomorphism. For instance, when
, one has
In general, one has the identity
for all natural numbers and
,
, where
range over all injections
,
with
. Combinatorially, the identity (2) follows from the fact that given any injections
and
with total image
of cardinality
, one has
, and furthermore there exist precisely
triples
of injections
,
,
such that
and
.
Example 1 When
, one has
which is just a restatement of the identity
Note that the coefficients appearing in (2) do not depend on the final number of variables . We may therefore abstract the role of
from the law (2) by introducing the real algebra
of formal sums
where for each ,
is an element of
(with only finitely many of the
being non-zero), and with the formal symbol
being formally linear, thus
and
for and scalars
, and with multiplication given by the analogue
of (2). Thus for instance, in this algebra we have
and
Informally, is an abstraction (or “inverse limit”) of the concept of a symmetric function of an unspecified number of variables, which are formed by summing terms that each involve only a bounded number of these variables at a time. One can check (somewhat tediously) that
is indeed a commutative real algebra, with a unit
. (I do not know if this algebra has previously been studied in the literature; it is somewhat analogous to the abstract algebra of finite linear combinations of Schur polynomials, with multiplication given by a Littlewood-Richardson rule. )
For natural numbers , there is an obvious specialisation map
from
to
, defined by the formula
Thus, for instance, maps
to
and
to
. From (2) and (3) we see that this map
is an algebra homomorphism, even though the maps
and
are not homomorphisms. By inspecting the
component of
we see that the homomorphism
is in fact surjective.
Now suppose that we have a measure on the space
, which then induces a product measure
on every product space
. To avoid degeneracies we will assume that the integral
is strictly positive. Assuming suitable measurability and integrability hypotheses, a function
can then be integrated against this product measure to produce a number
In the event that arises as a lift
of another function
, then from Fubini’s theorem we obtain the formula
is an element of the formal algebra , then
Note that by hypothesis, only finitely many terms on the right-hand side are non-zero.
Now for a key observation: whereas the left-hand side of (6) only makes sense when is a natural number, the right-hand side is meaningful when
takes a fractional value (or even when it takes negative or complex values!), interpreting the binomial coefficient
as a polynomial
in
. As such, this suggests a way to introduce a “virtual” concept of a symmetric function on a fractional power space
for such values of
, and even to integrate such functions against product measures
, even if the fractional power
does not exist in the usual set-theoretic sense (and
similarly does not exist in the usual measure-theoretic sense). More precisely, for arbitrary real or complex
, we now define
to be the space of abstract objects
with and
(and
now interpreted as formal symbols, with the structure of a commutative real algebra inherited from
, thus
In particular, the multiplication law (2) continues to hold for such values of , thanks to (3). Given any measure
on
, we formally define a measure
on
with regards to which we can integrate elements
of
by the formula (6) (providing one has sufficient measurability and integrability to make sense of this formula), thus providing a sort of “fractional dimensional integral” for symmetric functions. Thus, for instance, with this formalism the identities (4), (5) now hold for fractional values of
, even though the formal space
no longer makes sense as a set, and the formal measure
no longer makes sense as a measure. (The formalism here is somewhat reminiscent of the technique of dimensional regularisation employed in the physical literature in order to assign values to otherwise divergent integrals. See also this post for an unrelated abstraction of the integration concept involving integration over supercommutative variables (and in particular over fermionic variables).)
Example 2 Suppose
is a probability measure on
, and
is a random variable; on any power
, we let
be the usual independent copies of
on
, thus
for
. Then for any real or complex
, the formal integral
can be evaluated by first using the identity
(cf. (1)) and then using (6) and the probability measure hypothesis
to conclude that
For
a natural number, this identity has the probabilistic interpretation
whenever
are jointly independent copies of
, which reflects the well known fact that the sum
has expectation
and variance
. One can thus view (7) as an abstract generalisation of (8) to the case when
is fractional, negative, or even complex, despite the fact that there is no sensible way in this case to talk about
independent copies
of
in the standard framework of probability theory.
In this particular case, the quantity (7) is non-negative for every nonnegative
, which looks plausible given the form of the left-hand side. Unfortunately, this sort of non-negativity does not always hold; for instance, if
has mean zero, one can check that
and the right-hand side can become negative for
. This is a shame, because otherwise one could hope to start endowing
with some sort of commutative von Neumann algebra type structure (or the abstract probability structure discussed in this previous post) and then interpret it as a genuine measure space rather than as a virtual one. (This failure of positivity is related to the fact that the characteristic function of a random variable, when raised to the
power, need not be a characteristic function of any random variable once
is no longer a natural number: “fractional convolution” does not preserve positivity!) However, one vestige of positivity remains: if
is non-negative, then so is
One can wonder what the point is to all of this abstract formalism and how it relates to the rest of mathematics. For me, this formalism originated implicitly in an old paper I wrote with Jon Bennett and Tony Carbery on the multilinear restriction and Kakeya conjectures, though we did not have a good language for working with it at the time, instead working first with the case of natural number exponents and appealing to a general extrapolation theorem to then obtain various identities in the fractional
case. The connection between these fractional dimensional integrals and more traditional integrals ultimately arises from the simple identity
(where the right-hand side should be viewed as the fractional dimensional integral of the unit against
). As such, one can manipulate
powers of ordinary integrals using the machinery of fractional dimensional integrals. A key lemma in this regard is
Lemma 3 (Differentiation formula) Suppose that a positive measure
on
depends on some parameter
and varies by the formula
for some function
. Let
be any real or complex number. Then, assuming sufficient smoothness and integrability of all quantities involved, we have
for all
that are independent of
. If we allow
to now depend on
also, then we have the more general total derivative formula
again assuming sufficient amounts of smoothness and regularity.
Proof: We just prove (10), as (11) then follows by same argument used to prove the usual product rule. By linearity it suffices to verify this identity in the case for some symmetric function
for a natural number
. By (6), the left-hand side of (10) is then
Differentiating under the integral sign using (9) we have
and similarly
where are the standard
copies of
on
:
By the product rule, we can thus expand (12) as
where we have suppressed the dependence on for brevity. Since
, we can write this expression using (6) as
where is the symmetric function
But from (2) one has
and the claim follows.
Remark 4 It is also instructive to prove this lemma in the special case when
is a natural number, in which case the fractional dimensional integral
can be interpreted as a classical integral. In this case, the identity (10) is immediate from applying the product rule to (9) to conclude that
One could in fact derive (10) for arbitrary real or complex
from the case when
is a natural number by an extrapolation argument; see the appendix of my paper with Bennett and Carbery for details.
Let us give a simple PDE application of this lemma as illustration:
Proposition 5 (Heat flow monotonicity) Let
be a solution to the heat equation
with initial data
a rapidly decreasing finite non-negative Radon measure, or more explicitly
for al
. Then for any
, the quantity
is monotone non-decreasing in
for
, constant for
, and monotone non-increasing for
.
Proof: By a limiting argument we may assume that is absolutely continuous, with Radon-Nikodym derivative a test function; this is more than enough regularity to justify the arguments below.
For any , let
denote the Radon measure
Then the quantity can be written as a fractional dimensional integral
Observe that
and thus by Lemma 3 and the product rule
where we use for the variable of integration in the factor space
of
.
To simplify this expression we will take advantage of integration by parts in the variable. Specifically, in any direction
, we have
and hence by Lemma 3
Multiplying by and integrating by parts, we see that
where we use the Einstein summation convention in . Similarly, if
is any reasonable function depending only on
, we have
and hence on integration by parts
We conclude that
and thus by (13)
The choice of that then achieves the most cancellation turns out to be
(this cancels the terms that are linear or quadratic in the
), so that
. Repeating the calculations establishing (7), one has
and
where is the random variable drawn from
with the normalised probability measure
. Since
, one thus has
This expression is clearly non-negative for , equal to zero for
, and positive for
, giving the claim. (One could simplify
here as
if desired, though it is not strictly necessary to do so for the proof.)
Remark 6 As with Remark 4, one can also establish the identity (14) first for natural numbers
by direct computation avoiding the theory of fractional dimensional integrals, and then extrapolate to the case of more general values of
. This particular identity is also simple enough that it can be directly established by integration by parts without much difficulty, even for fractional values of
.
A more complicated version of this argument establishes the non-endpoint multilinear Kakeya inequality (without any logarithmic loss in a scale parameter ); this was established in my previous paper with Jon Bennett and Tony Carbery, but using the “natural number
first” approach rather than using the current formalism of fractional dimensional integration. However, the arguments can be translated into this formalism without much difficulty; we do so below the fold. (To simplify the exposition slightly we will not address issues of establishing enough regularity and integrability to justify all the manipulations, though in practice this can be done by standard limiting arguments.)
— 1. Multilinear heat flow monotonicity —
Before we give a multilinear variant of Proposition 5 of relevance to the multilinear Kakeya inequality, we first need to briefly set up the theory of finite products
of fractional powers of spaces , where
are real or complex numbers. The functions
to integrate here lie in the tensor product space
which is generated by tensor powers
with , with the usual tensor product identifications and algebra operations. One can evaluate fractional dimensional integrals of such functions against “virtual product measures”
, with
a measure on
, by the natural formula
assuming sufficient measurability and integrability hypotheses. We can lift functions to an element
of the space (15) by the formula
This is easily seen to be an algebra homomorphism.
Example 7 If
and
are functions and
are measures on
respectively, then (assuming sufficient measurability and integrability) then the multiple fractional dimensional integral
is equal to
In the case that
are natural numbers, one can view the “virtual” integrand
here as an actual function on
, namely
in which case the above evaluation of the integral can be achieved classically.
From a routine application of Lemma 3 and various forms of the product rule, we see that if each varies with respect to a time parameter
by the formula
and is a time-varying function in (15), then (assuming sufficient regularity and integrability), the time derivative
Now suppose that for each space one has a non-negative measure
, a vector-valued function
, and a matrix-valued function
taking values in real symmetric positive semi-definite
matrices. Let
be positive real numbers; we make the abbreviations
For any and
, we define the modified measures
and then the product fractional power measure
If we then define the heat-type functions
(where we drop the normalising power of for simplicity) we see in particular that
hence we can interpret the multilinear integral in the left-hand side of (17) as a product fractional dimensional integral. (We remark that in my paper with Bennett and Carbery, a slightly different parameterisation is used, replacing with
, and also replacing
with
.)
If the functions were constant in
, then the functions
would obey some heat-type partial differential equation, and the situation is now very analogous to Proposition 5 (and is also closely related to Brascamp-Lieb inequalities, as discussed for instance in this paper of Carlen, Lieb, and Loss, or this paper of mine with Bennett, Carbery, and Christ). However, for applications to the multilinear Kakeya inequality, we permit
to vary slightly in the
variable, and now the
do not directly obey any PDE.
A naive extension of Proposition 5 would then seek to establish monotonicity of the quantity (17). While such monotonicity is available in the “Brascamp-Lieb case” of constant , as discussed in the above papers, this does not quite seem to be to be true for variable
. To fix this problem, a weight is introduced in order to avoid having to take matrix inverses (which are not always available in this algebra). On the product fractional dimensional space
, we have a matrix-valued function
defined by
The determinant is then a scalar element of the algebra (15). We then define the quantity
Example 8 Suppose we take
and let
be natural numbers. Then
can be viewed as the
-matrix valued function
By slight abuse of notation, we write the determinant
of a
matrix as
, where
and
are the first and second rows of
. Then
and after some calculation, one can then write
as
By a polynomial extrapolation argument, this formula is then also valid for fractional values of
; this can also be checked directly from the definitions after some tedious computation. Thus we see that while the compact-looking fractional dimensional integral (18) can be expressed in terms of more traditional integrals, the formulae get rather messy, even in the
case. As such, the fractional dimensional calculus (based heavily on derivative identities such as (16)) gives a more convenient framework to manipulate these otherwise quite complicated expressions.
Suppose the functions are close to constant
matrices
, in the sense that
uniformly on for some small
(where we use for instance the operator norm to measure the size of matrices, and we allow implied constants in the
notation to depend on
, and the
). Then we can write
for some bounded matrix
, and then we can write
We can therefore write
where and the coefficients of the matrix
are some polynomial combination of the coefficients of
, with all coefficients in this polynomial of bounded size. As a consequence, and on expanding out all the fractional dimensional integrals, one obtains a formula of the form
Thus, as long as is strictly positive definite and
is small enough, this quantity
is comparable to the classical integral
Now we compute the time derivative of . We have
so by (16), one can write as
where we use as the coordinate for the copy of
that is being lifted to
.
As before, we can take advantage of some cancellation in this expression using integration by parts. Since
where are the standard basis for
, we see from (16) and integration by parts that
with the usual summation conventions on the index . Also, similarly to before, we suppose we have an element
of (15) for each
that does not depend on
, then by (16) and integration by parts
or, writing ,
We can thus write (20) as
where is the element of (15) given by
The terms in that are quadratic in
cancel. The linear term can be rearranged as
To cancel this, one would like to set equal to
Now in the commutative algebra (15), the inverse does not necessarily exist. However, because of the weight factor
, one can work instead with the adjugate matrix
, which is such that
where
is the identity matrix. We therefore set
equal to the expression
and now the expression in (22) does not contain any linear or quadratic terms in . In particular it is completely independent of
, and thus we can write
where is an arbitrary element of
that we will select later to obtain a useful cancellation. We can rewrite this a little as
If we now introduce the matrix functions
and the vector functions
then this can be rewritten as
Similarly to (19), suppose that we have
uniformly on , where
, thus we can write
for some bounded matrix-valued functions . Inserting this into the previous expression (and expanding out
appropriately) one can eventually write
where
and is some polynomial combination of the
and
(or more precisely, of the quantities
,
,
,
) that is quadratic in the
variables, with bounded coefficients. As a consequence, after expanding out the product fractional dimensional integrals and applying some Cauchy-Schwarz to control cross-terms, we have
Now we simplify . We let
be the average value of ; for each
this is just a vector in
. We then split
, leading to the identities
and
The term is problematic, but we can eliminate it as follows. By construction one has (supressing the dependence on
)
By construction, one has
Thus if is positive definite and
is small enough, this matrix is invertible, and we can choose
so that the expression
vanishes. Making this choice, we then have
Observe that the fractional dimensional integral of
or
for and arbitrary constant matrices
against
vanishes. As a consequence, we can now simplify the integral
Using (2), we can split
as the sum of
and
The latter also integrates to zero by the mean zero nature of . Thus we have simplified (24) to
Now let us make the key hypothesis that the matrix
is strictly positive definite, or equivalently that
for all , where the ordering is in the sense of positive definite matrices. Then we have the pointwise bound
and thus
For small enough, the expression inside the
is non-negative, and we conclude the monotonicity
We have thus proven the following statement, which is essentially Proposition 4.1 of my paper with Bennett and Carbery:
Proposition 9 Let
, let
be positive semi-definite real symmetric
matrices, and let
be such that
for
. Then for any positive measure spaces
with measures
and any functions
on
with
for a sufficiently small
, the quantity
is non-decreasing in
, and is also equal to
In particular, we have
for any
.
A routine calculation shows that for reasonable choices of (e.g. discrete measures of finite support), one has
and hence (setting ) we have
If we choose the to be the sum of
Dirac masses, and each
to be the diagonal matrix
, then the key condition (25) is obeyed for
, and one arrives at the multilinear Kakeya inequality
whenever are infinite tubes in
of width
and oriented within
of the basis vector
, for a sufficiently small absolute constant
. (The hypothesis on the directions can then be relaxed to a transversality hypothesis by applying some linear transformations and the triangle inequality.)

21 comments
Comments feed for this article
29 June, 2019 at 8:42 pm
Anonymous
What are the main ideas? And what are you trying to achieve with the complex mathematics?
30 June, 2019 at 8:16 am
Anonymous
“One can wonder what the point is to all of this abstract formalism and how it relates to the rest of mathematics…” — Prof. Tao.
Some of us, I think, do not understand what you are doing here. Please explain to us in plain English, your goals and main ideas here. And maybe then, we can better appreciate the high-level mathematics associated with your ideas.
30 June, 2019 at 9:29 am
Anonymous
FYI: Please gather some information at the link below:
https://en.wikipedia.org/wiki/Kakeya_set
I hope it helps you.
1 July, 2019 at 11:46 am
Anonymous
Thanks! It helps a bit. That link is quite interesting! And I understand some of its content.
But ‘Symmetric functions in a fractional number of variables, and the multilinear Kakeya conjecture’ is generally beyond me, and it is probably meant for the elite few or insiders (highly specialized audience)…
C’est la vie.
26 July, 2019 at 6:42 pm
Anonymous
The ability to learn and the ability to absorb/understand complex or advanced mathematical ideas are a big part of any mathematician’s toolbox to solve problems or to do advanced research…
Please try solving some Diophantine equations (DEs) using two or more distinct variables (you may use parts of example 1 above as a starting point) to get some feel for the theory posted here.
And rethink (construct a counterexample or develop a different or simpler disproof or develop a general algorithm that solves DEs efficiently, etc.) the solution/disproof of David Hilbert’s Tenth Problem for inspiration and for purpose of learning/research. And good luck!
29 June, 2019 at 11:18 pm
Tony Carbery
Ron Blei did a lot of work on fractional cartesian products in the mid-1970’s to the mid 1980’s. Is there a connection with his work?
30 June, 2019 at 10:54 am
Terence Tao
Interesting (and I now remember that you actually had put this reference into our original paper and I had forgotten about it!). Looking at Blei’s work, it seems that he is focused on constructing fractal subsets of ambient Cartesian product spaces (such as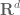 ) which exhibit dimensional properties similar to that which one would expect a fractional Cartesian power to obey. The constructions here are more focused on the integration theory than the dimensional theory, but it could well be that when the exponent
) which exhibit dimensional properties similar to that which one would expect a fractional Cartesian power to obey. The constructions here are more focused on the integration theory than the dimensional theory, but it could well be that when the exponent  is a fraction
is a fraction  then it is possible to find some more classical interpretation of these products, and of the fractional dimensional integral of symmetric functions, in a manner similar to what Blei does, and
then it is possible to find some more classical interpretation of these products, and of the fractional dimensional integral of symmetric functions, in a manner similar to what Blei does, and
29 June, 2019 at 11:44 pm
Allen Knutson
I haven’t done any calculations, but this is reminding me of Deligne’s tensor category of type A_n, n fractional. I’ll report back if it pans out.
29 June, 2019 at 11:52 pm
reader
What would we obtain if we were out for anti-symmetric functions in the first instance?
30 June, 2019 at 11:12 am
Terence Tao
Hmm, interesting question. From a representation theory perspective, symmetric functions correspond to Young diagrams consisting of one row, whereas antisymmetric functions correspond to Young diagrams consisting of one column. In this post we are focusing on trying to extend to situations where the horizontal dimensions of the Young diagram are fractional (perhaps related to this previous post: https://terrytao.wordpress.com/2017/09/05/continuous-analogues-of-the-schur-and-skew-schur-polynomials/ , now that I think about it) but if one were to try to do the same for antisymmetric functions then one would now also want to consider Young diagrams whose vertical dimensions are fractional. Perhaps this could be done, but it may require a somewhat different formalism than what is done here.
30 June, 2019 at 3:06 am
sylvainjulien
There must be a typo under your example 1, cause you define a quantity by setting it equal to itself.
[Corrected, thanks – T.]
30 June, 2019 at 8:29 am
L
@Allen_knutson Exactly what I was thinking. Etingoff’s work as well Representation theory in Complex dimension.
30 June, 2019 at 9:09 am
Anonymous
typo: The connection to ONE of these fractional dimensional integrals with more traditional integrals ultimately arises from the simple identity
[Reworded, thanks – T.]
30 June, 2019 at 11:21 pm
Anonymous
Is there a “natural” generalization of these concepts to the case of complex variables and complex valued functions?
Perhaps the concept of “symmetric function” should be replaced by a properly defined concept of “Hermitian complex valued function” ?
2 July, 2019 at 3:26 am
gpecc
The definition of![[F^{(k)}]_{k\rightarrow p}](https://s0.wp.com/latex.php?latex=%5BF%5E%7B%28k%29%7D%5D_%7Bk%5Crightarrow+p%7D&bg=ffffff&fg=545454&s=0&c=20201002) is what in Probability/Statistics is called a “symmetric U-statistic” with kernel
is what in Probability/Statistics is called a “symmetric U-statistic” with kernel 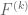 , based on a sample of dimension
, based on a sample of dimension  . U-statistics appear e.g. in parametric estimation, stochastic geometry, analysis of boolean functions, multiple stochastic integration, … It is intriguing to know that one can formally define symmetric U-statistics based on samples with fractional dimension…
. U-statistics appear e.g. in parametric estimation, stochastic geometry, analysis of boolean functions, multiple stochastic integration, … It is intriguing to know that one can formally define symmetric U-statistics based on samples with fractional dimension…
2 July, 2019 at 9:00 am
Terence Tao
Thanks for this link to existing terminology! (Though it seems that the symmetric U-statistic actually corresponds to a normalised average that in my notation would be![\binom{p}{k}^{-1} [F^{(k)}]_{k \to p}](https://s0.wp.com/latex.php?latex=%5Cbinom%7Bp%7D%7Bk%7D%5E%7B-1%7D+%5BF%5E%7B%28k%29%7D%5D_%7Bk+%5Cto+p%7D&bg=ffffff&fg=545454&s=0&c=20201002) .)
.)
8 July, 2019 at 2:02 pm
p kothari
On random topic, what are your thoughts about What are your thoughts on analyzing Pauli–Lubanski pseudovector and spin number(information geometry) in NLP vectorized framework – doc2vec etc. to detect fake news?
8 July, 2019 at 5:17 pm
YY
How would he know?
29 July, 2019 at 10:30 am
Sharp bounds for multilinear curved Kakeya, restriction and oscillatory integral estimates away from the endpoint | What's new
[…] original proof of this proceeded using a heat flow monotonicity method, which in my previous post I reinterpreted using a “virtual integration” concept on a fractional Cartesian product […]
21 August, 2019 at 6:29 pm
tt
typo: The integrand on the left-hand side of (5) is![[x_1 x_2]_{2 \to p}](https://s0.wp.com/latex.php?latex=%5Bx_1+x_2%5D_%7B2+%5Cto+p%7D&bg=ffffff&fg=545454&s=0&c=20201002) .
.
[Corrected, thanks – T.]
15 April, 2020 at 8:04 pm
Lior Silberman
This is highly reminiscent of Razborov’s theory of flag algebras for extremal combinatorics.