A family of sets for some
is a sunflower if there is a core set
contained in each of the
such that the petal sets
are disjoint. If
, let
denote the smallest natural number with the property that any family of
distinct sets of cardinality at most
contains
distinct elements
that form a sunflower. The celebrated Erdös-Rado theorem asserts that
is finite; in fact Erdös and Rado gave the bounds
. This remains open at present despite much effort (including a Polymath project); after a long series of improvements to the upper bound, the best general bound known currently is
, established in 2019 by Rao (building upon a recent breakthrough a month previously of Alweiss, Lovett, Wu, and Zhang). Here we remove the easy cases
or
in order to make the logarithmic factor
a little cleaner.
Rao’s argument used the Shannon noiseless coding theorem. It turns out that the argument can be arranged in the very slightly different language of Shannon entropy, and I would like to present it here. The argument proceeds by locating the core and petals of the sunflower separately (this strategy is also followed in Alweiss-Lovett-Wu-Zhang). In both cases the following definition will be key. In this post all random variables, such as random sets, will be understood to be discrete random variables taking values in a finite range. We always use boldface symbols to denote random variables, and non-boldface for deterministic quantities.
Definition 1 (Spread set) Let. A random set
is said to be
-spread if one has
for all sets
. A family
of sets is said to be
-spread if
is non-empty and the random variable
is
-spread, where
is drawn uniformly from
.
The core can then be selected greedily in such a way that the remainder of a family becomes spread:
Lemma 2 (Locating the core) Letbe a family of subsets of a finite set
, each of cardinality at most
, and let
. Then there exists a “core” set
of cardinality at most
such that the set
has cardinality at least
, and such that the family
is
-spread. Furthermore, if
and the
are distinct, then
.
Proof: We may assume is non-empty, as the claim is trivial otherwise. For any
, define the quantity
Let be the set (3). Since
,
is non-empty. It remains to check that the family
is
-spread. But for any
and
drawn uniformly at random from
one has
In view of the above lemma, the bound (2) will then follow from
Proposition 3 (Locating the petals) Letbe natural numbers, and suppose that
for a sufficiently large constant
. Let
be a finite family of subsets of a finite set
, each of cardinality at most
which is
-spread. Then there exist
such that
is disjoint.
Indeed, to prove (2), we assume that is a family of sets of cardinality greater than
for some
; by discarding redundant elements and sets we may assume that
is finite and that all the
are contained in a common finite set
. Apply Lemma 2 to find a set
of cardinality
such that the family
is
-spread. By Proposition 3 we can find
such that
are disjoint; since these sets have cardinality
, this implies that the
are distinct. Hence
form a sunflower as required.
Remark 4 Proposition 3 is easy to prove if we strengthen the condition onto
. In this case, we have
for every
, hence by the union bound we see that for any
with
there exists
such that
is disjoint from the set
, which has cardinality at most
. Iterating this, we obtain the conclusion of Proposition 3 in this case. This recovers a bound of the form
, and by pursuing this idea a little further one can recover the original upper bound (1) of Erdös and Rado.
It remains to prove Proposition 3. In fact we can locate the petals one at a time, placing each petal inside a random set.
Proposition 5 (Locating a single petal) Let the notation and hypotheses be as in Proposition 3. Letbe a random subset of
, such that each
lies in
with an independent probability of
. Then with probability greater than
,
contains one of the
.
To see that Proposition 5 implies Proposition 3, we randomly partition into
by placing each
into one of the
,
chosen uniformly and independently at random. By Proposition 5 and the union bound, we see that with positive probability, it is simultaneously true for all
that each
contains one of the
. Selecting one such
for each
, we obtain the required disjoint petals.
We will prove Proposition 5 by gradually increasing the density of the random set and arranging the sets to get quickly absorbed by this random set. The key iteration step is
Proposition 6 (Refinement inequality) Letand
. Let
be a random subset of a finite set
which is
-spread, and let
be a random subset of
independent of
, such that each
lies in
with an independent probability of
. Then there exists another
-spread random subset
of
whose support is contained in the support of
, such that
and
Note that a direct application of the first moment method gives only the bound
One can iterate the above proposition, repeatedly replacing with
(noting that this preserves the
-spread nature of
) to conclude
Corollary 7 (Iterated refinement inequality) Let,
, and
. Let
be a random subset of a finite set
which is
-spread, and let
be a random subset of
independent of
, such that each
lies in
with an independent probability of
. Then there exists another random subset
of
with support contained in the support of
, such that
Now we can prove Proposition 5. Let be chosen shortly. Applying Corollary 7 with
drawn uniformly at random from the
, and setting
, or equivalently
, we have
It remains to establish Proposition 6. This is the difficult step, and requires a clever way to find the variant of
that has better containment properties in
than
does. The main trick is to make a conditional copy
of
that is conditionally independent of
subject to the constraint
. The point here is that this constrant implies the inclusions
-spread hypothesis, it is hard for
to contain any fixed large set. If we could apply this observation in the contrapositive to
we could hope to get a good upper bound on the size of
and hence on
thanks to (4). One can also hope to improve such an upper bound by also employing (5), since it is also hard for the random set
to contain a fixed large set. There are however difficulties with implementing this approach due to the fact that the random sets
are coupled with
in a moderately complicated fashion. In Rao’s argument a somewhat complicated encoding scheme was created to give information-theoretic control on these random variables; below the fold we accomplish a similar effect by using Shannon entropy inequalities in place of explicit encoding. A certain amount of information-theoretic sleight of hand is required to decouple certain random variables to the extent that the Shannon inequalities can be effectively applied. The argument bears some resemblance to the “entropy compression method” discussed in this previous blog post; there may be a way to more explicitly express the argument below in terms of that method. (There is also some kinship with the method of dependent random choice, which is used for instance to establish the Balog-Szemerédi-Gowers lemma, and was also translated into information theoretic language in these unpublished notes of Van Vu and myself.)
— 1. Shannon entropy —
In this section we lay out all the tools from the theory of Shannon entropy that we will need.
Define an empirical sequence for a random variable taking values in a discrete set
to be a sequence
in
such that the empirical samples of this sequence converge in distribution to
in the sense that
, where
is a uniform random variable drawn from
, and
denotes a quantity that goes to zero as
(uniformly over other parameters independent of
). Every random variable
has at least one empirical sequence; indeed, from the strong law of large numbers one can find such a sequence almost surely by taking an infinite number of independent trials of
.
If is a random variable taking values in some set
, its Shannon entropy
is defined by the formula
We record the following standard and easily verified facts:
Lemma 8 (Basic Shannon inequalities) Letbe random variables.
- (i) (Monotonicity) If
is a deterministic function
of
, then
. More generally, if
is a deterministic function
of
and
, then
. If
is a deterministic function of
, then
.
- (ii) (Subadditivity) One has
, with equality iff
,
are independent. More generally, one has
, with equality iff
,
are conditionally independent with respect to
.
- (iii) (Chain rule) One has
. More generally
. In particular
, and
iff
are independent; similarly,
, and
iff
are conditionally independent with respect to
.
- (iv) (Jensen’s inequality) If
takes values in a finite set
then
, with equality iff
is uniformly distributed in
. More generally, if
takes values in a set
that depends on
, then
, with equality iff
is uniformly distributed in
after conditioning on
.
- (v) (Gibbs inequality) If
take values in the same finite set
, then
(we permit the right-hand side to be infinite, which makes the inequality vacuously true).
See this previous blog post for some intuitive analogies to understand Shannon entropy.
Now we establish some inequalities of relevance to random sets.
We first observe that any small random set largely determines any of its subsets. Define a random subset of a random set to be a random set
such that
holds almost surely.
Lemma 9 (Subsets of small sets have small conditional entropy) Letbe a random finite set.
- (i) One has
for any random subset
of
.
- (ii) One has
. If
is almost surely non-empty, we can improve this to
.
Proof: The set takes values in the power set
of
, so the claim (i) follows from Lemma 8(iv). (Note how it is convenient here that we are using the base
for the logarithm.)
For (ii), apply Lemma 8(v) with and
the geometric random variable
for natural numbers
(or
for positive
, if
is non-empty).
Now we encode the property of a random variable being
-spread in the language of Shannon entropy.
Lemma 10 (Information-theoretic interpretation of spread) Letbe a random finite set that is
-spread for some
.
- (i) If
is uniformly distributed amongst some finite collection
of sets, then
for all random subsets
of
.
- (ii) In the general case, if
are an empirical sequence of
, then
as
, where
is drawn uniformly from
and
is a random subset of
.
Informally: large random subsets of an -spread set
necessarily have a lot of mutual information with
. Conversely, one can bound the size of a random subset of an
-spread set by bounding its mutual information with
.
Proof: In case (i), it suffices by Lemma 8(iv) to establish the bound
Given a finite non-empty set and
, let
denote the collection of
-element subsets of
. A uniformly chosen element
of
is thus a random
-element subset of
; we refer to the quantity
as the density of this random subset, and
as a uniformly chosen random subset of
of density
. (Of course, this is only defined when
is an integer multiple of
.) Uniformly chosen random sets have the following information-theoretic relationships to small random sets:
Lemma 11 Letbe a finite non-empty set, let
be a uniformly chosen random subset of
of some density
(which is a multiple of
).
- (i) (Spread) If
is a random subset of
, then
- (ii) (Absorption) If
is a random subset of
, then
Proof: To prove (i), it suffices by Lemma 10(i) to show that is
-spread, which amounts to showing that
For (ii), by replacing with
we may assume that
are disjoint. From Lemma 8(iii) and Lemma 9(ii) it suffices to show that
The following “relative product” construction will be important for us. Given a random variable and a deterministic function
of that variable, one can construct a conditionally independent copy
of
subject to the condition
, with the joint distribution
— 2. Proof of refinement inequality —
Now we have enough tools to prove Proposition 6. Let be as in that proposition. If
is in the support of
we can set
so we can instead assume that
is never empty. In particular
In order to use Lemma 10 we fix an empirical sequence for
. We relabel
as
, and let
be a parameter going off to infinity (so in particular
is identified with a subset of
. We let
be drawn uniformly at random from
, and let
be a uniform random subset of
of density
independent of
. Observe from Stirling’s formula that
converges in distribution to
. Thus it will suffice to find another uniform random variable
from
such that
, since we can pass to a subsequence in which
converges in distribution to
. From (8) we have
From we can form the random set
; we then form a conditionally independent copy
of
subject to the constraint
as the uniform variable to establish (9). The point is that the relation (11) implies that
Now, from the constraints (11), (13) we have

31 comments
Comments feed for this article
20 July, 2020 at 10:11 pm
David Roberts
The formatting around the two uses of Erdős’ name in the first paragraph is broken.
[Corrected, thanks – T.]
21 July, 2020 at 5:04 pm
David Roberts
Unfortunately, though the diacritics are fixed, the link doesn’t stop where it’s meant to!
[Corrected, thanks – T.]
26 July, 2020 at 10:29 am
Max
There is one more spare ‘}’ too much in that link text (“… theorem}”).
21 July, 2020 at 4:40 am
Darko Veljan
Let G=(V,E) be a connected graph, n=#V. Let I be a subset of V with k el (“infected” vertices); let N(v) be the nbhd of v; suppose #N(v)<r+1 for all v.. Let J be the set of all vertices at distance at most s from infected vertices. What are bounds of probability that a random vertex will be infected
Answer (perhaps could be a better one). Between k/n and k[1+r+r(r-1)+r(r-1)^2+…+r(r-1)^(s-1)]/n. Exponential in s= distance from infected vertices.
21 July, 2020 at 5:40 am
Anonymous
Dear Pro Tao,
Has Sunflower conjecture been solved completely? If not still yet, I expect good news from you. I am really excited to read your paper like watching a football match.
Thank sir,
24 July, 2020 at 1:53 pm
Dmitriy Zakharov
Thank you for the great post! Here are some typos I spotted:
In the proof of Lemma 11 V should be instead of W and S instead of X in some binomial coefficients.
In (11) take union instead of intersection.
“and hence by Lemma 8(i): …” In the formula below this line W’ should be instead of W.
After “we can form the random variable”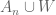 instead of
instead of 
Missing “=” after “so we can also rewrite the above conditional entropy as”
[Corrected, thanks – T.]
26 July, 2020 at 12:08 pm
Anonymous
A natural generalization of the concept of “Sunflower” to a family of multisets is to similarly define under the additional constraint that the multiplicity of each element in any multiset is at most
under the additional constraint that the multiplicity of each element in any multiset is at most 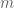 . Clearly
. Clearly  .
. can be expressed as a function of
can be expressed as a function of  and
and 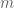 ?
?
Is it possible that
27 July, 2020 at 4:22 am
Max
On the bottom of the Polymath wiki page, the section and table with f(k,r) appears to have k and r reversed w.r.t. here and the upper half of the page. (It says f(k,r) = k^r +… while we have here and earlier on the page Sun(k,r) ~ r^k.) I don’t know whom to contact for this, but the main author of the page is https://asone.ai/polymath/index.php?title=User:Teorth with user page signed(?) “Terence Tao”, so maybe …?
[Corrected, thanks – T.]
27 July, 2020 at 8:01 am
Max
(Note that in the paper by Kostochka et al., where the formula appears as “k^r”, r is the cardinality of the sets and k is the number of petals — the converse of what k & r stand for here and on the Polymath wiki page!)
27 July, 2020 at 3:41 pm
rafik zeraoulia
@Terry Tao, I ask if there is any relationship between Szemerédi’s theorem and Sunflower conjecture?
pleas check my question here:
https://mathoverflow.net/q/366245/51189
Thanks
1 August, 2020 at 7:18 am
a
Why is writing down things in information theoretic parlance better?
2 August, 2020 at 4:53 pm
Terence Tao
The bounds are a little sharper and I found the argument to be somewhat less ad hoc when presented in this language as it is largely based on piecing together various basic estimates using the Shannon entropy inequalities (although the trick of passing to a conditional copy twice to get a good bound still feels somewhat magical to me).
1 August, 2020 at 7:14 pm
Lutz Warnke
Minor typo: in the proof of Proposition 5, below Corollary 7 I believe it should read E |A’ \ V| < 1/r (to obtain the claimed probability via Markov).
[Corrected, thanks – T.]
2 August, 2020 at 5:01 am
Is there any relationship between Szemerédi's theorem and Sunflower conjecture? ~ MathOverflow ~ mathubs.com
[…] rate. In the same time it is an open problem to determine the exact rate growth or exact bounds for The sunflower (the sunflower lemma via Shannon entropy). My question here […]
3 August, 2020 at 11:28 pm
Yuval Filmus
The proof of Lemma 10(i) uses Jensen’s inequality in the wrong direction.
[Here we are using the equality case of Jensen’s inequality (crucially relying on the uniform distribution of ) – T.]
) – T.]
5 August, 2020 at 11:30 am
Amazing: Ryan Alweiss, Shachar Lovett, Kewen Wu, Jiapeng Zhang made dramatic progress on the Sunflower Conjecture | Combinatorics and more
[…] Updates: (from comments below) Anup Rao presents a simplification of the original Alweiss, Lovett, Wu, and Zhang argument. https://arxiv.org/abs/1909.04774; An excellent Quanta Magazine article by Kevin Hartnett https://www.quantamagazine.org/mathematicians-begin-to-tame-wild-sunflower-problem-20191021/ . Terry Tao posted a version of Rao’s proof https://terrytao.wordpress.com/2020/07/20/the-sunflower-lemma-via-shannon-entropy/. […]
11 August, 2020 at 9:01 am
T
Could someone please explain what it means to say ‘ is now conditionally independent of
is now conditionally independent of 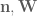 relative to
relative to 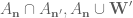 ? I read this to mean that when we fix
? I read this to mean that when we fix  and
and 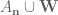 , then the random variable m conditioned on these is independent from the random variables
, then the random variable m conditioned on these is independent from the random variables  and
and  conditioned on these. But I don’t understand why we no longer condition on the events in (13). Is it just notation? So when you write the entropy of
conditioned on these. But I don’t understand why we no longer condition on the events in (13). Is it just notation? So when you write the entropy of 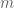 conditioned on
conditioned on  , then you actually mean the constraint
, then you actually mean the constraint  ? Thanks!
? Thanks!
14 August, 2020 at 7:35 am
Terence Tao
The constraints in (13) hold almost surely, they do not need to be conditioned on further. ( is a conditionally independent copy of
is a conditionally independent copy of  subject to (13), which is not the same as an unconditionally independent copy that is then conditioned to (13); see the discussion at the end of Section 1.)
subject to (13), which is not the same as an unconditionally independent copy that is then conditioned to (13); see the discussion at the end of Section 1.)
13 August, 2020 at 4:32 pm
The Ionescu-Wainger multiplier theorem and the adeles | What's new
[…] losses in (i), and recent progress on the Erdos-Rado sunflower conjecture (as discussed in this recent post) to improve the bounds in (ii). For (i), the key point is that one can express a sum such […]
25 September, 2020 at 6:56 am
Lutz Warnke
In case someone finds it useful, let me remark that a very minor variant of the existing probabilistic arguments yields an upper bound of form Sun(k,r) \le (Cr \log k)^k for k,r \ge 2.
This was observed during a 2020 REU with undergrads Tolson Bell and Suchakree Chueluecha,
and the minor twist is to randomly partition X into 2r sets V_1,…,V_{2r} (instead of r sets).
Indeed, for R \ge C r \log k and fixed j, the proof of Proposition 5 then shows that V_j contains at least one of the A_i with probability at least 1/2 whenever the universal constant C is sufficiently large (this can also be deduced from Lemma 4 in Rao’s paper).
The expected number of sets V_j containing at least one of the A_i is thus at least 2r * 1/2 = r, ensuring that the required r disjoint sets A_{i_1}, \ldots, A_{i_r} must exist.
This establishes Proposition 3 for R \ge C r \log k, which in turn gives the claimed upper bound Sun(k,r) \le (Cr \log k)^k, see also https://arxiv.org/abs/2009.09327
28 April, 2021 at 9:23 pm
Lunjia Hu
Thank you for the great post! Here is a minor technical issue I spotted:
At the beginning of Section 2: proof of refinement inequality, conditioning on the event that is non-empty may cause the resulting distribution to be no longer
is non-empty may cause the resulting distribution to be no longer 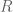 -spread. This can be fixed by setting
-spread. This can be fixed by setting  deterministically whenever
deterministically whenever 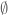 is in the support of
is in the support of  . Of course, this could make the distribution of
. Of course, this could make the distribution of  different from that of
different from that of  and thus violate a desired property of Proposition 6, but for the purpose of proving Proposition 5, we only need the weaker property that the support of
and thus violate a desired property of Proposition 6, but for the purpose of proving Proposition 5, we only need the weaker property that the support of  is contained in the support of
is contained in the support of  .
.
[Correction implemented, thanks – T.]
19 May, 2021 at 3:04 pm
Entropy Estimation via Two Chains: Streamlining the Proof of the Sunflower Lemma – Theory Dish
[…] of this blog post is to present a streamlined proof of Theorem 1. The proof is largely based on a blog post by Terence Tao where he presented an elegant proof of Rao’s result using Shannon entropy. […]
16 June, 2021 at 12:30 am
How to write LaTeX on a static blog smoothly? ~ TeX - LaTeX ~ AsktoWorld.com
[…] look of the blogpost I’m targeting is similar to this blog or this one. But anything goes if it’s easy to setup and […]
30 July, 2021 at 6:17 am
DeepC
A minor correction : in the last line of the proof of Lemma 2, is in the wrong direction : that would imply
is in the wrong direction : that would imply  .
.
Rather, one should say that if , then the probability is indeed
, then the probability is indeed 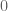 . Therefore,
. Therefore, 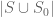 is in fact
is in fact 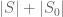 .
.
[Corrected, thanks – T.]
16 November, 2021 at 9:25 am
Is there any relationship between Szemerédi's theorem and Sunflower conjecture? ~ MathOverflow ~ InsideDarkWeb.com
[…] rate. In the same time it is an open problem to determine the exact rate growth or exact bounds for The sunflower (the sunflower lemma via Shannon entropy). My question here […]
26 April, 2022 at 10:50 am
M Stoeckl
I am confused by the part where Proposition 6 is used to prove Corollary 7. If anyone could help explain this, it would be much appreciated.
What precisely does replacing with
with  mean?
mean?  is a random variable (which may also depend on
is a random variable (which may also depend on  ), but the statement of Prop 6 requires that
), but the statement of Prop 6 requires that  be a finite set.
be a finite set.
1 May, 2022 at 9:55 am
Terence Tao
This is the conditioning trick. For each possible value of
of  , condition all the random variables to the event
, condition all the random variables to the event  , apply Proposition 6 to the deterministic finite set
, apply Proposition 6 to the deterministic finite set 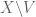 and the conditioned random variables, and then use the law of total probability to undo the conditioning.
and the conditioned random variables, and then use the law of total probability to undo the conditioning.
2 May, 2022 at 7:04 pm
M Stoeckl
Thank you, that was very helpful.
Also, you may be interested to hear that it is possible to improve the constant in Proposition 6 from to
to  , where
, where 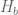 is the binary entropy function. The approach I used is to modify Lunjia Hu’s proof of Proposition 6, to directly study the case where
is the binary entropy function. The approach I used is to modify Lunjia Hu’s proof of Proposition 6, to directly study the case where  is a random subset with each
is a random subset with each 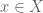 contained in
contained in  with independent probability
with independent probability 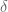 , instead of having
, instead of having  be a random set of size $\delta |X|$. Much of the improvement comes from having a tighter version of the absorption property.
be a random set of size $\delta |X|$. Much of the improvement comes from having a tighter version of the absorption property.
I’ve written up this argument as part of https://mstoeckl.com/notes/research/sunflower_notes.html .
18 September, 2022 at 12:24 am
Anonymous
Sorry, I don’t follow the first inequality in the second last inequality. More specificly, I don’t see where the $A_{n’}\setminus A_{n}$ come from in $H(W|A_{n’}\setminus A_n)$. Could someone explain it to me?
19 September, 2022 at 8:26 pm
Terence Tao
Oops, this is actually a rather serious issue; I had thought that and
and  determine
determine  , when instead they determine
, when instead they determine  . It does not seem easy to implement a local fix for ths issue; however there are now better proofs of this lemma that do not proceed using this second independent copy that give better bounds, starting with this argument of Hu and this refinement of Stoeckl. I’ll leave the original post unchanged for the historical record.
. It does not seem easy to implement a local fix for ths issue; however there are now better proofs of this lemma that do not proceed using this second independent copy that give better bounds, starting with this argument of Hu and this refinement of Stoeckl. I’ll leave the original post unchanged for the historical record.
19 September, 2022 at 11:23 pm
Anonymous
Thanks, I’ll take a look at their proofs.