Kaisa Matomäki, Maksym Radziwill, Joni Teräväinen, Tamar Ziegler and I have uploaded to the arXiv our paper Higher uniformity of bounded multiplicative functions in short intervals on average. This paper (which originated from a working group at an AIM workshop on Sarnak’s conjecture) focuses on the local Fourier uniformity conjecture for bounded multiplicative functions such as the Liouville function 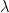{\lambda}. One form of this conjecture is the assertion that

\displaystyle \int_0^X \| \lambda \|_{U^k([x,x+H])}\ dx = o(X) \ \ \ \ \ (1)

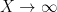
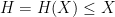
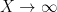
as {X \rightarrow \infty} for any fixed {k \geq 0} and any {H = H(X) \leq X} that goes to infinity as {X \rightarrow \infty}, where {U^k([x,x+H])} is the (normalized) Gowers uniformity norm. Among other things this conjecture implies (logarithmically averaged version of) the Chowla and Sarnak conjectures for the Liouville function (or the Möbius function), see this previous blog post.

The conjecture gets more difficult as {k} increases, and also becomes more difficult the more slowly {H} grows with {X}. The {k=0} conjecture is equivalent to the assertion

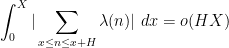
\displaystyle \int_0^X |\sum_{x \leq n \leq x+H} \lambda(n)| \ dx = o(HX)

which was proven (for arbitrarily slowly growing {H}) in a landmark paper of Matomäki and Radziwill, discussed for instance in this blog post.

For 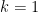{k=1}, the conjecture is equivalent to the assertion

\displaystyle \int_0^X \sup_\alpha |\sum_{x \leq n \leq x+H} \lambda(n) e(-\alpha n)| \ dx = o(HX). \ \ \ \ \ (2)

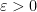
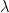
This remains open for sufficiently slowly growing {H} (and it would be a major breakthrough in particular if one could obtain this bound for {H} as small as {\log^\varepsilon X} for any fixed {\varepsilon>0}, particularly if applicable to more general bounded multiplicative functions than {\lambda}, as this would have new implications for a generalization of the Chowla conjecture known as the Elliott conjecture). Recently, Kaisa, Maks and myself were able to establish this conjecture in the range {H \geq X^\varepsilon} (in fact we have since worked out in the current paper that we can get {H} as small as {\exp(\log^{5/8+\varepsilon} X)}). In our current paper we establish Fourier uniformity conjecture for higher {k} for the same range of {H}. This in particular implies local orthogonality to polynomial phases,

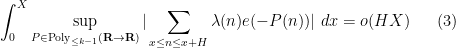
\displaystyle \int_0^X \sup_{P \in \mathrm{Poly}_{\leq k-1}({\bf R} \rightarrow {\bf R})} |\sum_{x \leq n \leq x+H} \lambda(n) e(-P(n))| \ dx = o(HX) \ \ \ \ \ (3)

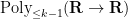
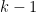
 where {\mathrm{Poly}_{\leq k-1}({\bf R} \rightarrow {\bf R})} denotes the polynomials of degree at most {k-1}, but the full conjecture is a bit stronger than this, establishing the more general statement

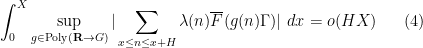
\displaystyle \int_0^X \sup_{g \in \mathrm{Poly}({\bf R} \rightarrow G)} |\sum_{x \leq n \leq x+H} \lambda(n) \overline{F}(g(n) \Gamma)| \ dx = o(HX) \ \ \ \ \ (4)

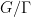
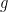
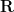
 for any degree {k} filtered nilmanifold {G/\Gamma} and Lipschitz function {F: G/\Gamma \rightarrow {\bf C}}, where {g} now ranges over polynomial maps from {{\bf R}} to {G}. The method of proof follows the same general strategy as in the previous paper with Kaisa and Maks. (The equivalence of (4) and (1) follows from the inverse conjecture for the Gowers norms, proven in this paper.) We quickly sketch first the proof of (3), using very informal language to avoid many technicalities regarding the precise quantitative form of various estimates. If the estimate (3) fails, then we have the correlation estimate

\displaystyle |\sum_{x \leq n \leq x+H} \lambda(n) e(-P_x(n))| \gg H

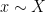
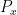
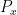
for many {x \sim X} and some polynomial {P_x} depending on {x}. The difficulty here is to understand how {P_x} can depend on {x}. We write the above correlation estimate more suggestively as

\displaystyle \lambda(n) \sim_{[x,x+H]} e(P_x(n)).

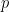
Because of the multiplicativity {\lambda(np) = -\lambda(p)} at small primes {p}, one expects to have a relation of the form

\displaystyle e(P_{x'}(p'n)) \sim_{[x/p,x/p+H/p]} e(P_x(pn)) \ \ \ \ \ (5)

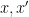
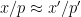
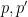
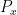
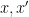
 for many {x,x'} for which {x/p \approx x'/p'} for some small primes {p,p'}. (This can be formalised using an inequality of Elliott related to the Turan-Kubilius theorem.) This gives a relationship between {P_x} and {P_{x'}} for “edges” {x,x'} in a rather sparse “graph” connecting the elements of say {[X/2,X]}. 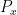Using some graph theory one can locate some non-trivial “cycles” in this graph that eventually lead (in conjunction to a certain technical but important “Chinese remainder theorem” step to modify the {P_x} to eliminate a rather serious “aliasing” issue that was already discussed in this previous post) to obtain functional equations of the form

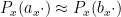
\displaystyle P_x(a_x \cdot) \approx P_x(b_x \cdot)

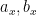
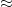
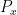
for some large and close (but not identical) integers {a_x,b_x}, where {\approx} should be viewed as a first approximation (ignoring a certain “profinite” or “major arc” term for simplicity) as “differing by a slowly varying polynomial” and the polynomials {P_x} should now be viewed as taking values on the reals rather than the integers. This functional equation can be solved to obtain a relation of the form

\displaystyle P_x(t) \approx T_x \log t

for some real number {T_x} of polynomial size, and with further analysis of the relation (5) one can make {T_x} basically independent of {x}. This simplifies (3) to something like

\displaystyle \int_0^X \sup_{P \in \mathrm{Poly}_{\leq k-1}({\bf R} \rightarrow {\bf R})} |\sum_{x \leq n \leq x+H} \lambda(n) n^{-iT}| \ dx = o(HX)

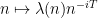
and this is now of a form that can be treated by the theorem of Matomäki and Radziwill (because {n \mapsto \lambda(n) n^{-iT}} is a bounded multiplicative function). (Actually because of the profinite term mentioned previously, one also has to insert a Dirichlet character of bounded conductor into this latter conclusion, but we will ignore this technicality.)

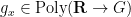Now we apply the same strategy to (4). For abelian {G} the claim follows easily from (3), so we focus on the non-abelian case. One now has a polynomial sequence {g_x \in \mathrm{Poly}({\bf R} \rightarrow G)} attached to many 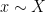{x \sim X}, and after a somewhat complicated adaptation of the above arguments one again ends up with an approximate functional equation

\displaystyle g_x(a_x \cdot) \Gamma \approx g_x(b_x \cdot) \Gamma \ \ \ \ \ (6)

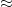
where the relation {\approx} is rather technical and will not be detailed here. A new difficulty arises in that there are some unwanted solutions to this equation, such as

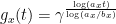
\displaystyle g_x(t) = \gamma^{\frac{\log(a_x t)}{\log(a_x/b_x)}}

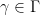
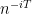
for some {\gamma \in \Gamma}, which do not necessarily lead to multiplicative characters like {n^{-iT}} as in the polynomial case, but instead to some unfriendly looking “generalized multiplicative characters” (think of {e(\lfloor \alpha \log n \rfloor \beta \log n)} as a rough caricature). To avoid this problem, we rework the graph theory portion of the argument to produce not just one functional equation of the form (6)for each {x}, but many, leading to dilation invariances

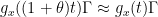
\displaystyle g_x((1+\theta) t) \Gamma \approx g_x(t) \Gamma

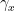
for a “dense” set of {\theta}. From a certain amount of Lie algebra theory (ultimately arising from an understanding of the behaviour of the exponential map on nilpotent matrices, and exploiting the hypothesis that {G} is non-abelian) one can conclude that (after some initial preparations to avoid degenerate cases) {g_x(t)} must behave like {\gamma_x^{\log t}} for some central element {\gamma_x} of {G}. 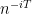This eventually brings one back to the multiplicative characters {n^{-iT}} that arose in the polynomial case, and the arguments now proceed as before.

We give two applications of this higher order Fourier uniformity. One regards the growth of the number

\displaystyle s(k) := |\{ (\lambda(n+1),\dots,\lambda(n+k)): n \in {\bf N} \}|

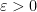
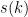
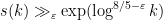
of length {k} sign patterns in the Liouville function. The Chowla conjecture implies that {s(k) = 2^k}, but even the weaker conjecture of Sarnak that {s(k) \gg (1+\varepsilon)^k} for some {\varepsilon>0} remains open. 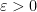Until recently, the best asymptotic lower bound on {s(k)} was {s(k) \gg k^2}, due to McNamara; with our result, we can now show {s(k) \gg_A k^A} for any {A} (in fact we can get {s(k) \gg_\varepsilon \exp(\log^{8/5-\varepsilon} k)} for any {\varepsilon>0}). The idea is to repeat the now-standard argument to exploit multiplicativity at small primes to deduce Chowla-type conjectures from Fourier uniformity conjectures, noting that the Chowla conjecture would give all the sign patterns one could hope for. The usual argument here uses the “entropy decrement argument” to eliminate a certain error term (involving the large but mean zero factor {p 1_{p|n}-1}). However the observation is that if there are extremely few sign patterns of length {k}, then the entropy decrement argument is unnecessary (there isn’t much entropy to begin with), and a more low-tech moment method argument (similar to the derivation of Chowla’s conjecture from Sarnak’s conjecture, as discussed for instance in this post) gives enough of Chowla’s conjecture to produce plenty of length {k} sign patterns. If there are not extremely few sign patterns of length {k} then we are done anyway. One quirk of this argument is that the sign patterns it produces may only appear exactly once; in contrast with preceding arguments, we were not able to produce a large number of sign patterns that each occur infinitely often.

The second application is to obtain cancellation for various polynomial averages involving the Liouville function 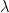{\lambda} or von Mangoldt function 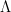{\Lambda}, such as

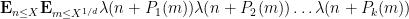
\displaystyle {\bf E}_{n \leq X} {\bf E}_{m \leq X^{1/d}} \lambda(n+P_1(m)) \lambda(n+P_2(m)) \dots \lambda(n+P_k(m))

or

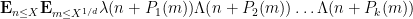
\displaystyle {\bf E}_{n \leq X} {\bf E}_{m \leq X^{1/d}} \lambda(n+P_1(m)) \Lambda(n+P_2(m)) \dots \Lambda(n+P_k(m))

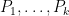
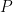
where {P_1,\dots,P_k} are polynomials of degree at most {d}, no two of which differ by a constant (the latter is essential to avoid having to establish the Chowla or Hardy-Littlewood conjectures, which of course remain open). 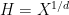Results of this type were previously obtained by Tamar Ziegler and myself in the “true complexity zero” case when the polynomials {P} had distinct degrees, in which one could use the {k=0} theory of Matomäki and Radziwill; now that higher {k} is available at the scale {H=X^{1/d}} we can now remove this restriction.