Abdul Basit, Artem Chernikov, Sergei Starchenko, Chiu-Minh Tran and I have uploaded to the arXiv our paper Zarankiewicz’s problem for semilinear hypergraphs. This paper is in the spirit of a number of results in extremal graph theory in which the bounds for various graph-theoretic problems or results can be greatly improved if one makes some additional hypotheses regarding the structure of the graph, for instance by requiring that the graph be “definable” with respect to some theory with good model-theoretic properties.
A basic motivating example is the question of counting the number of incidences between points and lines (or between points and other geometric objects). Suppose one has points and
lines in a space. How many incidences can there be between these points and lines? The utterly trivial bound is
, but by using the basic fact that two points determine a line (or two lines intersect in at most one point), a simple application of Cauchy-Schwarz improves this bound to
. In graph theoretic terms, the point is that the bipartite incidence graph between points and lines does not contain a copy of
(there does not exist two points and two lines that are all incident to each other). Without any other further hypotheses, this bound is basically sharp: consider for instance the collection of
points and
lines in a finite plane
, that has
incidences (one can make the situation more symmetric by working with a projective plane rather than an affine plane). If however one considers lines in the real plane
, the famous Szemerédi-Trotter theorem improves the incidence bound further from
to
. Thus the incidence graph between real points and lines contains more structure than merely the absence of
.
More generally, bounding on the size of bipartite graphs (or multipartite hypergraphs) not containing a copy of some complete bipartite subgraph (or
in the hypergraph case) is known as Zarankiewicz’s problem. We have results for all
and all orders of hypergraph, but for sake of this post I will focus on the bipartite
case.
In our paper we improve the bound to a near-linear bound in the case that the incidence graph is “semilinear”. A model case occurs when one considers incidences between points and axis-parallel rectangles in the plane. Now the
condition is not automatic (it is of course possible for two distinct points to both lie in two distinct rectangles), so we impose this condition by fiat:
Theorem 1 Suppose one haspoints and
axis-parallel rectangles in the plane, whose incidence graph contains no
‘s, for some large
.
- (i) The total number of incidences is
.
- (ii) If all the rectangles are dyadic, the bound can be improved to
.
- (iii) The bound in (ii) is best possible (up to the choice of implied constant).
We don’t know whether the bound in (i) is similarly tight for non-dyadic boxes; the usual tricks for reducing the non-dyadic case to the dyadic case strangely fail to apply here. One can generalise to higher dimensions, replacing rectangles by polytopes with faces in some fixed finite set of orientations, at the cost of adding several more logarithmic factors; also, one can replace the reals by other ordered division rings, and replace polytopes by other sets of bounded “semilinear descriptive complexity”, e.g., unions of boundedly many polytopes, or which are cut out by boundedly many functions that enjoy coordinatewise monotonicity properties. For certain specific graphs we can remove the logarithmic factors entirely. We refer to the preprint for precise details.
The proof techniques are combinatorial. The proof of (i) relies primarily on the order structure of to implement a “divide and conquer” strategy in which one can efficiently control incidences between
points and rectangles by incidences between approximately
points and boxes. For (ii) there is additional order-theoretic structure one can work with: first there is an easy pruning device to reduce to the case when no rectangle is completely contained inside another, and then one can impose the “tile partial order” in which one dyadic rectangle
is less than another
if
and
. The point is that this order is “locally linear” in the sense that for any two dyadic rectangles
, the set
is linearly ordered, and this can be exploited by elementary double counting arguments to obtain a bound which eventually becomes
after optimising certain parameters in the argument. The proof also suggests how to construct the counterexample in (iii), which is achieved by an elementary iterative construction.

12 comments
Comments feed for this article
11 September, 2020 at 11:44 am
zeraoulia Rafik
@Dear prof Tao , You have claimed in paragraph or section 2 that the famous Szemerédi-Trotter theorem improve the incidence bounds further n^(3/2) to O(n^{4/3}) but in wikipedia for Szemerédi-Trotter theorem the incidence bound can’t be improved , except in terms of the implicit constants, I want to explain me how this ? or probably you mean the exception case namely implicit constant which it is not clear to me , Thanks
13 September, 2020 at 10:37 am
Terence Tao
Just a short update: Tomon and Zakharov have now used the counterexample construction in Theorem 1(iii) to disprove a recent conjecture of Alon, Basavaraju, Chandran, Mathew, and Rajendraprasad regarding the maximal possible number of edges in a graph of a given separation dimension and number of vertices.
13 September, 2020 at 5:41 pm
arch1
What does it mean for an incidence graph to be “semilinear”?
14 September, 2020 at 9:16 am
Terence Tao
It means that the incidence relation can be defined using a finite number of linear inequalities (over some suitable ordered ring). (Here the “semi-” prefix is in the same sense as “semi-algebraic set“.) For instance, to describe the incidences between a set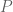 of points in the plane and a set
of points in the plane and a set 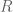 of rectangles, one can view
of rectangles, one can view 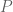 as a collection of pairs
as a collection of pairs 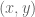 in
in 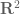 , and
, and 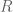 as a collection of quadruples
as a collection of quadruples 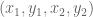 in
in 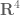 , and the incidence relation is then given by the linear inequalities
, and the incidence relation is then given by the linear inequalities  and
and 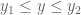 .
.
14 September, 2020 at 4:10 pm
arch1
Thank you.
16 September, 2020 at 5:52 pm
Anonymous
Noice
13 October, 2020 at 7:17 am
Anonymous
why the prop2.8 need condition ‘finite’? where the condition is applied in the proof?
13 October, 2020 at 1:33 pm
Terence Tao
Ah, right, this condition is in fact never used, it can be safely deleted.
7 November, 2020 at 6:25 pm
HongJun Ge
Dear prof Tao, in remark4.7 how can you prove that the probability is larger than 10^(-10)?
8 November, 2020 at 10:03 pm
Terence Tao
Ah, this claim turns out to be not quite true as stated; one needs to use a non-isotropic dilation in which the x and y coordinates are multiplied by different dilation factors, rather than the isotropic dilation currently written, in order to have a positive probability of the rectangle being approximately dyadic. Basically a horizontal dilation will make (with positive probability) the horizontal side length close to a power of two (say between $1.001$ and $1.002$ times a power of two), a vertical dilation will achieve a similar effect for the vertical side length, and then a random translation will then place the rectangle very close to a dyadic rectangle with positive probability.
12 November, 2020 at 4:26 am
arslanahmedphm
@Dear Prof Tao , Suppose we have a point p(a,b) a and b are given and let L be a line s.t p(a,b) belong to L
By this information can we know the equation of L in terms of P(a.b) ?can it gives as more information about L?
24 February, 2021 at 7:48 pm
HongJun Ge
Dear prof Tao. In section 5 we define a_cB means dim(a/BC)=dim(a/C). What’s the meaning of BC?
[This is notation (common in model theory) for the union of $B$ and $C$. -T]