As someone who had a relatively light graduate education in algebra, the import of Yoneda’s lemma in category theory has always eluded me somewhat; the statement and proof are simple enough, but definitely have the “abstract nonsense” flavor that one often ascribes to this part of mathematics, and I struggled to connect it to the more grounded forms of intuition, such as those based on concrete examples, that I was more comfortable with. There is a popular MathOverflow post devoted to this question, with many answers that were helpful to me, but I still felt vaguely dissatisfied. However, recently when pondering the very concrete concept of a polynomial, I managed to accidentally stumble upon a special case of Yoneda’s lemma in action, which clarified this lemma conceptually for me. In the end it was a very simple observation (and would be extremely pedestrian to anyone who works in an algebraic field of mathematics), but as I found this helpful to a non-algebraist such as myself, and I thought I would share it here in case others similarly find it helpful.
In algebra we see a distinction between a polynomial form (also known as a formal polynomial), and a polynomial function, although this distinction is often elided in more concrete applications. A polynomial form in, say, one variable with integer coefficients, is a formal expression of the form
are coefficients in the integers, and
is an indeterminate: a symbol that is often intended to be interpreted as an integer, real number, complex number, or element of some more general ring
, but is for now a purely formal object. The collection of such polynomial forms is denoted
, and is a commutative ring.
A polynomial form can be interpreted in any ring
(even non-commutative ones) to create a polynomial function
, defined by the formula
. This definition (2) looks so similar to the definition (1) that we usually abuse notation and conflate
with
. This conflation is supported by the identity theorem for polynomials, that asserts that if two polynomial forms
agree at an infinite number of (say) complex numbers, thus
for infinitely many
, then they agree
as polynomial forms (i.e., their coefficients match). But this conflation is sometimes dangerous, particularly when working in finite characteristic. For instance:
- (i) The linear forms
and
are distinct as polynomial forms, but agree when interpreted in the ring
, since
for all
.
- (ii) Similarly, if
is a prime, then the degree one form
and the degree
form
are distinct as polynomial forms (and in particular have distinct degrees), but agree when interpreted in the ring
, thanks to Fermat’s little theorem.
- (iii) The polynomial form
has no roots when interpreted in the reals
, but has roots when interpreted in the complex numbers
. Similarly, the linear form
has no roots when interpreted in the integers
, but has roots when interpreted in the rationals
.
The above examples show that if one only interprets polynomial forms in a specific ring , then some information about the polynomial could be lost (and some features of the polynomial, such as roots, may be “invisible” to that interpretation). But this turns out not to be the case if one considers interpretations in all rings simultaneously, as we shall now discuss.
If are two different rings, then the polynomial functions
and
arising from interpreting a polynomial form
in these two rings are, strictly speaking, different functions. However, they are often closely related to each other. For instance, if
is a subring of
, then
agrees with the restriction of
to
. More generally, if there is a ring homomorphism
from
to
, then
and
are intertwined by the relation
was an inclusion homomorphism. Another example comes from the complex conjugation automorphism
on the complex numbers, in which case (3) asserts the identity
What was surprising to me (as someone who had not internalized the Yoneda lemma) was that the converse statement was true: if one had a function associated to every ring
that obeyed the intertwining relation
, then there was a unique polynomial form
such that
for all rings
. This seemed surprising to me because the functions
were a priori arbitrary functions, and as an analyst I would not expect them to have polynomial structure. But the fact that (4) holds for all rings
and all homomorphisms
is in fact rather powerful. As an analyst, I am tempted to proceed by first working with the ring
of complex numbers and taking advantage of the aforementioned identity theorem, but this turns out to be tricky because
does not “talk” to all the other rings
enough, in the sense that there are not always as many ring homomorphisms from
to
as one would like. But there is in fact a more elementary argument that takes advantage of a particularly relevant (and “talkative”) ring to the theory of polynomials, namely the ring
of polynomials themselves. Given any other ring
, and any element
of that ring, there is a unique ring homomorphism
from
to
that maps
to
, namely the evaluation map
We have thus created an identification of form and function: polynomial forms are in one-to-one correspondence with families of functions
obeying the intertwining relation (4). But this identification can be interpreted as a special case of the Yoneda lemma, as follows. There are two categories in play here: the category
of rings (where the morphisms are ring homomorphisms), and the category
of sets (where the morphisms are arbitrary functions). There is an obvious forgetful functor
between these two categories that takes a ring and removes all of the algebraic structure, leaving behind just the underlying set. A collection
of functions (i.e.,
-morphisms) for each
in
that obeys the intertwining relation (4) is precisely the same thing as a natural transformation from the forgetful functor
to itself. So we have identified formal polynomials in
as a set with natural endomorphisms of the forgetful functor:
What does this have to do with Yoneda’s lemma? Well, remember that every element of a ring
came with an evaluation homomorphism
. Conversely, every homomorphism from
to
will be of the form
for a unique
– indeed,
will just be the image of
under this homomorphism. So the evaluation homomorphism provides a one-to-one correspondence between elements of
, and ring homomorphisms in
. This correspondence is at the level of sets, so this gives the identification

17 comments
Comments feed for this article
25 August, 2023 at 6:45 am
Anonymous
There is an exponenet p missing in when you mention Fermat’s little theorem
when you mention Fermat’s little theorem
[Corrected, thanks – T.]
25 August, 2023 at 6:49 am
thebirdreader
“the degree p form n” -> “the degree p form n^p”\
[Corrected, thanks – T.]
25 August, 2023 at 7:36 am
Rex
I think of the Yoneda lemma and the functor of points perspective as being the algebraic analogue of an analytic notion which you are very familiar with: distributions.
Any smooth, compactly-supported function on the real line defines a distribution by the formula![f \longmapsto [\cdot,f]](https://s0.wp.com/latex.php?latex=f+%5Clongmapsto+%5B%5Ccdot%2Cf%5D&bg=ffffff&fg=545454&s=0&c=20201002) where
where ![[\cdot,f]](https://s0.wp.com/latex.php?latex=%5B%5Ccdot%2Cf%5D&bg=ffffff&fg=545454&s=0&c=20201002) denotes the functional
denotes the functional  . The analytic version of the Yoneda lemma amounts to saying that this map from the class of functions to the class of distributions is injective.
. The analytic version of the Yoneda lemma amounts to saying that this map from the class of functions to the class of distributions is injective.
Note that the objects in the two settings are formally very similar. Just as a distribution is something which you integrate functions against to get a well-defined value, a “presheaf” (i.e. a contravariant functor from your category of interest to the category of sets) is something which you “integrate against” (meaning hom against) with objects in
to the category of sets) is something which you “integrate against” (meaning hom against) with objects in  to obtain a well-defined value (which in category theory means a set). The formula is the same:
to obtain a well-defined value (which in category theory means a set). The formula is the same: ![X \longmapsto [\cdot,X]](https://s0.wp.com/latex.php?latex=X+%5Clongmapsto+%5B%5Ccdot%2CX%5D&bg=ffffff&fg=545454&s=0&c=20201002) where
where ![[\cdot,X]](https://s0.wp.com/latex.php?latex=%5B%5Ccdot%2CX%5D&bg=ffffff&fg=545454&s=0&c=20201002) now means
now means  .
.
The reason for doing all of this abstract nonsense is the same as in analysis. In PDE, one runs into solutions and constructions which are not honest functions. So we are led to create settings of generalized functions where we can work with such objects and hopefully relate them to actual functions.
Similarly, in algebraic geometry, one runs into algebraic “spaces” which are not quite varieties (nor schemes, nor algebraic spaces, …), so one is forced to move to larger (and larger) categories of “generalized algebraic spaces” to incorporate the objects we encounter and treat them on an even footing with more classical varieties.
This process of generalization is necessary even to give rigorous grounding for very classical objects, such as the moduli space of smooth compact Riemann surfaces of genus
of smooth compact Riemann surfaces of genus  . Riemann knew of this moduli space and he could informally compute the dimension of
. Riemann knew of this moduli space and he could informally compute the dimension of  , but one must consider the functor of points they define (and a little bit beyond) to finally arrive at an object with the correct properties befitting the name of “moduli space of curves”.
, but one must consider the functor of points they define (and a little bit beyond) to finally arrive at an object with the correct properties befitting the name of “moduli space of curves”.
None of this resemblence is a coincidence, by the way. Schwartz was Grothendieck’s advisor.
25 August, 2023 at 2:24 pm
Anonymous
Is it possible to extend this identification between forms and function from polynomials to a larger class of formal power series (satisfying e.g. certain growth conditions on the coefficients)?
25 August, 2023 at 4:38 pm
Terence Tao
Formally, yes, though the correspondence is a bit strange. Consider for instance the ring![{\bf Z}[[\mathbf{n}]]](https://s0.wp.com/latex.php?latex=%7B%5Cbf+Z%7D%5B%5B%5Cmathbf%7Bn%7D%5D%5D&bg=ffffff&fg=545454&s=0&c=20201002) of formal power series with integer coefficients (with no constraint on convergence). The Yoneda lemma says that elements
of formal power series with integer coefficients (with no constraint on convergence). The Yoneda lemma says that elements  ring can be identified (as a set) with a family of functions
ring can be identified (as a set) with a family of functions  associated to each ring
associated to each ring  obeying the natural transformation rule, but this time instead of functions from
obeying the natural transformation rule, but this time instead of functions from  to
to  , they are functions from
, they are functions from ![\mathrm{Hom}({\bf Z}[[\mathbf{n}]], R)](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BHom%7D%28%7B%5Cbf+Z%7D%5B%5B%5Cmathbf%7Bn%7D%5D%5D%2C+R%29&bg=ffffff&fg=545454&s=0&c=20201002) to
to  , arising from evaluating a ring homomorphism from
, arising from evaluating a ring homomorphism from ![{\bf Z}[[\mathbf{n}]]](https://s0.wp.com/latex.php?latex=%7B%5Cbf+Z%7D%5B%5B%5Cmathbf%7Bn%7D%5D%5D&bg=ffffff&fg=545454&s=0&c=20201002) to
to  at
at  . Unfortunately the space
. Unfortunately the space ![\mathrm{Hom}({\bf Z}[[\mathbf{n}]], R)](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BHom%7D%28%7B%5Cbf+Z%7D%5B%5B%5Cmathbf%7Bn%7D%5D%5D%2C+R%29&bg=ffffff&fg=545454&s=0&c=20201002) is rather strange and not easy to describe, in contrast to
is rather strange and not easy to describe, in contrast to ![\mathrm{Hom}({\bf Z}[\mathbf{n}], R)](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BHom%7D%28%7B%5Cbf+Z%7D%5B%5Cmathbf%7Bn%7D%5D%2C+R%29&bg=ffffff&fg=545454&s=0&c=20201002) which is canonically identifiable with
which is canonically identifiable with  .
.
In general it seems the more analysis is present in one’s objects (e.g., infinite series, topology, smoothness, etc.), the less intuitive and reasonable the Yoneda lemma becomes. But perhaps there are still some surprising uses of that lemma in analytic categories…
25 August, 2023 at 6:25 pm
Z. M.
It might be conceptually more correct to look at the topological ring in place of the discrete ring. In other words, we look at endomorphisms of the functor
in place of the discrete ring. In other words, we look at endomorphisms of the functor  of taking the nilradical, often called the de Rham prestack.
of taking the nilradical, often called the de Rham prestack.
25 August, 2023 at 6:28 pm
Z. M.
Sorry, it should be called the formal affine line , not the de Rham prestack.
, not the de Rham prestack.
27 August, 2023 at 1:10 pm
Star
Hey, Terry! I got fascinated by your Masterclass course and have watched all of it!
Can you do yet another toned-down version for the public level like me? I just started at a really good manufacturing company so I really want something that I could apply on a real-life basis. Besides that, I’m barely aware that there are obviously *techniques *than dull-brained force involved in *motorcycle riding; *I barely got my license but am struggling starting from the car. I know I have to learn the KBB stuff eventually on my own, only that I’m so distracted throughout my day.
I’m not sure if you will actually get to read this reply, but here goes nothing.
Much Regards,
Star
29 August, 2023 at 11:46 pm
Anonymous
Is there a similar results for algebraic (multi)function (i.e. algebraic correspondence between variables) by considering the (formal) minimal polynomial representing this correspondence?
13 September, 2023 at 8:50 am
venkyclement
The polynomial P is a function from Z[n] to itself where n goes to P(n). But I do not see where we use the fact every element x of Z[n] needs to map to P(x). Why can’t I represent![F_{Z[n]}](https://s0.wp.com/latex.php?latex=F_%7BZ%5Bn%5D%7D&bg=ffffff&fg=545454&s=0&c=20201002) by an equivalence class of functions all of which map n to P(n) but could do something completely different for other elements of Z[n]. Thank you for a great post.
by an equivalence class of functions all of which map n to P(n) but could do something completely different for other elements of Z[n]. Thank you for a great post.
13 September, 2023 at 9:39 am
Anonymous
To be more explicit, I realize that building off a function that takes n to P(n) but other elements of Z[n] to something else may lead to functions in other rings that do not satisfy (4), but how do we know that a function that takes x to P(x) for all elements of Z[n] is the only function that does?
14 September, 2023 at 2:33 pm
Terence Tao
From applying the identity![\phi_{R,n}(F_{{\bf Z}[\mathrm{n}]}(\mathrm{n})) = F_R(n)](https://s0.wp.com/latex.php?latex=%5Cphi_%7BR%2Cn%7D%28F_%7B%7B%5Cbf+Z%7D%5B%5Cmathrm%7Bn%7D%5D%7D%28%5Cmathrm%7Bn%7D%29%29+%3D+F_R%28n%29&bg=ffffff&fg=545454&s=0&c=20201002) with
with ![R = {\bf Z}[\mathrm{n}]](https://s0.wp.com/latex.php?latex=R+%3D+%7B%5Cbf+Z%7D%5B%5Cmathrm%7Bn%7D%5D&bg=ffffff&fg=545454&s=0&c=20201002) ,
, 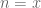 , and
, and ![P = F_{{\bf Z}[\mathrm{n}]}](https://s0.wp.com/latex.php?latex=P+%3D+F_%7B%7B%5Cbf+Z%7D%5B%5Cmathrm%7Bn%7D%5D%7D&bg=ffffff&fg=545454&s=0&c=20201002) we get
we get ![F_{{\bf Z}[\mathrm{n}]}(x) = P(x)](https://s0.wp.com/latex.php?latex=F_%7B%7B%5Cbf+Z%7D%5B%5Cmathrm%7Bn%7D%5D%7D%28x%29+%3D+P%28x%29&bg=ffffff&fg=545454&s=0&c=20201002) for any
for any ![x \in {\bf Z}[\mathrm{n}]](https://s0.wp.com/latex.php?latex=x+%5Cin+%7B%5Cbf+Z%7D%5B%5Cmathrm%7Bn%7D%5D&bg=ffffff&fg=545454&s=0&c=20201002) .
.
16 September, 2023 at 7:34 am
Anonymous
P ≥ 5 (mod6) professor Tao. ( I must insist )
This observation is interesting because it suggests that the sequence generates composite numbers composed exclusively of prime factors congruent to 1 or 5 modulo 6, leading to a unique structure reminiscent of polynomial forms.
In summary, by “reminiscent of polynomial forms,” I meant that the numbers in your sequence possess properties and characteristics that are akin to those of polynomial expressions in algebra. These properties include algebraic structure, prime factorization, unique composition, combinatorial operations, and a ring-like behavior. While not polynomials in the strict mathematical sense, they share some similarities in their mathematical behavior.
29 September, 2023 at 9:02 am
Anonymous
An interesting/trivial special case is replacing![Z[x]](https://s0.wp.com/latex.php?latex=Z%5Bx%5D&bg=ffffff&fg=545454&s=0&c=20201002) by the integer ring
by the integer ring 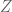 . Since there are only two possible ring homomorphisms: either a trivial map 0 or the unique map mapping 1 to the unity of the ring
. Since there are only two possible ring homomorphisms: either a trivial map 0 or the unique map mapping 1 to the unity of the ring  . Then Yoneda Lemma can be read as
. Then Yoneda Lemma can be read as  . Here
. Here  functor maps a ring
functor maps a ring  to
to 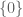 if R doesn’t have a unity or to $\{0, 1\}$ otherwise. Philosophically, it says “maps preserve discrete structure can by represented by the simplest discrete structure
if R doesn’t have a unity or to $\{0, 1\}$ otherwise. Philosophically, it says “maps preserve discrete structure can by represented by the simplest discrete structure 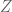 ” which is similar to professor Tao’s example: “maps preserve ring structure can be represented by the simplest algebraic structure
” which is similar to professor Tao’s example: “maps preserve ring structure can be represented by the simplest algebraic structure ![Z[x]](https://s0.wp.com/latex.php?latex=Z%5Bx%5D&bg=ffffff&fg=545454&s=0&c=20201002) ” :)
” :)
3 October, 2023 at 12:04 am
John Baez
By coincidence tomorrow I’m giving a talk about a categorified version of this whole set of ideas, based on work with Joe Moeller and Todd Trimble, and I’ve put my lecture notes here. A “2-rig” is a kind of category that has a way to multiply and add objects, with multiplication distributing over addition; the examples I’m interested in include the category of representations of a group or the category of vector bundles on a topological space, with tensor product as multiplication and direct sum as addition.
Just as polynomials are the free ring on one generator, the category of “Schur functors” is the free 2-rig on one object. And by an argument exactly paralleling the one you gave, Schur functors act naturally on the underlying category of any 2-rig. Examples include “taking the nth tensor power” or “taking the nth exterior power”. To carry out this argument we need a 2-categorical version of the Yoneda lemma. But in my talk, when it comes time to give the proof I’ll switch gears and do the humbler case of polynomials acting on rings, since that’s already interesting.
21 October, 2023 at 3:39 pm
Sébastien Martineau
Thanks a lot for sharing this insight, it has been very enlightening!
Inspired by your blog post and by the comment (*), here is a nice puzzle or exercice to toy around with, in the Yoneda philosophy.
Consider all unital rings. Call a “choice function” the data, for each unital ring, of an element in it. Say that a choice function x is “coherent” if, for any morphism of unital rings f : A –> B, we have x(B)=f(x(A)).
1. Find one coherent choice function.
2. Find another one.
3. Find infintely many choice functions.
4. It is very likely that you have now found all possible choice functions: try to prove it!
Technically speaking, this instance is more basic than the study of polynomials. However, we have to start right away with how to intertwine things, while the storytelling with polynomials can start with more familiar subtleties and bring very smoothly this notion of intertwining.
I stated the puzzle in the framework of unital rings. To me, its essence rather lies around the notion of marked group. I prefer giving the statement for unital rings because this framework is more widely known, and because I wanted to sweep markings under the carpet.
—
(*) : https://terrytao.wordpress.com/2023/08/25/yonedas-lemma-as-an-identification-of-form-and-function-the-case-study-of-polynomials/#comment-681873
21 October, 2023 at 3:58 pm
Sébastien Martineau
All questions 1-4 are about coherent choice functions (the word “coherent” is missing in 3 and 4).