Kevin Ford, Dimitris Koukoulopoulos and I have just uploaded to the arXiv our paper “A lower bound on the mean value of the Erdős-Hooley delta function“. This paper complements the recent paper of Dimitris and myself obtaining the upper bound

on the mean value of the
Erdős-Hooley delta function 
In this paper we obtain a lower bound
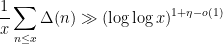
where
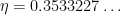
is an exponent that arose in previous work of
result of Ford, Green, and Koukoulopoulos, who showed that
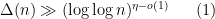
for all

outside of a set of density zero. The previous best known lower bound for the mean value was

due to Hall and Tenenbaum.
The point is the main contributions to the mean value of 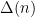 are driven not by “typical” numbers
are driven not by “typical” numbers  of some size
of some size  , but rather of numbers that have a splitting
, but rather of numbers that have a splitting
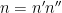
where

is the product of primes between some intermediate threshold
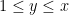
and

and behaves “typically” (so in particular, it has about

prime factors, as per the
Hardy-Ramanujan law and the
Erdős-Kac law, but
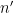
is the product of primes up to
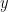
and has double the number of typical prime factors –

, rather than

– thus

is the type of number that would make a significant contribution to the mean value of the divisor function

. Here
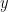
is such that

is an integer in the range
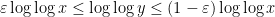
for some small constant
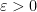
there are basically
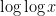
different values of
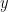
give essentially disjoint contributions. From the easy inequalities

(the latter coming from the pigeonhole principle) and the fact that
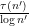
has mean about one, one would expect to get the above result provided that one could get a lower bound of the form
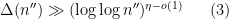
for most typical

with prime factors between
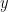
and

. Unfortunately, due to the lack of small prime factors in

, the arguments of Ford, Green, Koukoulopoulos that give
(1) for typical

do not quite work for the rougher numbers

. However, it turns out that one can get around this problem by replacing
(2) by the more efficient inequality

where

is an enlarged version of
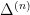
when
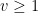
. This inequality is easily proven by applying the pigeonhole principle to the factors of

of the form
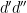
, where
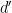
is one of the

factors of
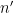
, and

is one of the
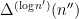
factors of

in the optimal interval
![{[e^u, e^{u+\log n'}]}](https://s0.wp.com/latex.php?latex=%7B%5Be%5Eu%2C+e%5E%7Bu%2B%5Clog+n%27%7D%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002)
. The extra room provided by the enlargement of the range
![{[e^u, e^{u+1}]}](https://s0.wp.com/latex.php?latex=%7B%5Be%5Eu%2C+e%5E%7Bu%2B1%7D%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002)
to
![{[e^u, e^{u+\log n'}]}](https://s0.wp.com/latex.php?latex=%7B%5Be%5Eu%2C+e%5E%7Bu%2B%5Clog+n%27%7D%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002)
turns out to be sufficient to adapt the Ford-Green-Koukoulopoulos argument to the rough setting. In fact we are able to use the main technical estimate from that paper as a “black box”, namely that if one considers a random subset

of
![{[D^c, D]}](https://s0.wp.com/latex.php?latex=%7B%5BD%5Ec%2C+D%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002)
for some small
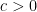
and sufficiently large
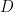
with each
![{n \in [D^c, D]}](https://s0.wp.com/latex.php?latex=%7Bn+%5Cin+%5BD%5Ec%2C+D%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002)
lying in

with an independent probability
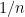
, then with high probability there should be

subset sums of

that attain the same value. (Initially, what “high probability” means is just “close to

“, but one can reduce the failure probability significantly as

by a “tensor power trick” taking advantage of Bennett’s inequality.)
are driven not by “typical” numbers
of some size
, but rather of numbers that have a splitting

9 comments
Comments feed for this article
23 August, 2023 at 8:48 pm
isaacg227
Looks like there’s a typo in the equation just after “In this paper we obtain a lower bound “. Thanks for the post!
[Corrected, thanks – T.]
23 August, 2023 at 8:59 pm
isaacg227
Similarly, the 1/x in front of the summations in the first two inequalities seem to be redundant with the x in front of the log log … on the right hand side of those inequalities.
[Corrected, thanks – T.]
23 August, 2023 at 10:32 pm
joe34
Is there a conjecture for tight bounds, or even an exact growth rate, between the 11/4=3.75 and the 1.353…? And what is your hunch on the sort of difficulty it requires? Thank you!
24 August, 2023 at 6:25 am
Terence Tao
Good question. My co-authors, who have worked more extensively with the Erdős-Hooley function than I have, are more inclined to conjecture that the exponent 1.353… is in fact the truth. I do not have a strong opinion here, though certainly I do not think the 11/4 exponent is optimal, as it comes from some clear limitations to our upper bound method (actually, I am surprised that our upper bound approach, based on the moment method, is as effective as it is).
24 August, 2023 at 12:26 am
Anonymous
It would be interesting to consider this problem for a generalization of the function to
to  where in the definition of
where in the definition of  the upper bound
the upper bound  is replaced by
is replaced by  for some fixed positive parameter
for some fixed positive parameter  (i.e. using a general “window” for the divisors d inthe definition)
(i.e. using a general “window” for the divisors d inthe definition)
24 August, 2023 at 6:28 am
Terence Tao
For , one has from the triangle inequality that
, one has from the triangle inequality that  , while similarly for
, while similarly for 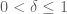 one has
one has  . So for fixed
. So for fixed  the asymptotics are not much different from the
the asymptotics are not much different from the  case, but it could be interesting to consider values of
case, but it could be interesting to consider values of  that grow or shrink with
that grow or shrink with  . For instance in the arguments of our paper it becomes important to consider a choice of
. For instance in the arguments of our paper it becomes important to consider a choice of  which is comparable to
which is comparable to 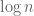 .
.
24 August, 2023 at 12:30 am
Anonymous
There appears to be a couple of typos with the co-author’s surname. It should be Koukoulopoulos instead of Koukoulopolous.
[Corrected, thanks – T.]
24 August, 2023 at 5:04 pm
Zach Hunter
Small typo in your writeup: “area” is written rather than “are” in Definition 1 on page 2.
[Thanks, this will be corrected in the next revision of the ms. -T]
8 November, 2023 at 6:20 am
ducduc2710
Can we use the ratio 𝜎(n+1)/𝜎(n) and the Lagarias inequality to prove RH? Dear Professor Terence Tao