I’ve just uploaded to the arXiv my paper “On product representations of squares“. This short paper answers (in the negative) a (somewhat obscure) question of Erdös. Namely, for any 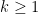 , let
, let  be the size of the largest subset
be the size of the largest subset  of
of 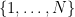 with the property that no
with the property that no  distinct elements of
distinct elements of  multiply to a square. In a paper by Erdös, Sárközy, and Sós, the following asymptotics were shown for fixed
multiply to a square. In a paper by Erdös, Sárközy, and Sós, the following asymptotics were shown for fixed  :
:
Thus the asymptotics for

for odd
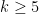
were not completely settled. Erdös asked if one had

for odd
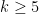
. The main result of this paper is that this is not the case; that is to say, there exists
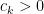
such that any subset

of
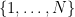
of cardinality at least

will contain

distinct elements that multiply to a square, if

is large enough. In fact, the argument works for all
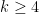
, although it is not new in the even case. I will also note that there are now quite sharp upper and lower bounds on
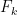
for even
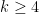
, using methods from graph theory: see
this recent paper of Pach and Vizer for the latest results in this direction. Thanks to the
results of Granville and Soundararajan, we know that the constant
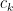
cannot exceed the
Hall-Montgomery constant 
and I (very tentatively) conjecture that this is in fact the optimal value for this constant. This looks somewhat difficult, but a more feasible conjecture would be that the
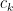
asymptotically approach the Hall-Montgomery constant as
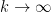
, since the aforementioned result of Granville and Soundararajan morally corresponds to the

case.
In the end, the argument turned out to be relatively simple; no advanced results from additive combinatorics, graph theory, or analytic number theory were required. I found it convenient to proceed via the probabilistic method (although the more combinatorial technique of double counting would also suffice here). The main idea is to generate a tuple  of distinct random natural numbers in
of distinct random natural numbers in 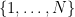 which multiply to a square, and which are reasonably uniformly distributed throughout
which multiply to a square, and which are reasonably uniformly distributed throughout 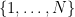 , in that each individual number
, in that each individual number  is attained by one of the random variables
is attained by one of the random variables  with a probability of
with a probability of 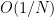 . If one can find such a distribution, then if the density of
. If one can find such a distribution, then if the density of  is sufficienly close to
is sufficienly close to  , it will happen with positive probability that each of the
, it will happen with positive probability that each of the  will lie in
will lie in  , giving the claim.
, giving the claim.
When 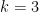 , this strategy cannot work, as it contradicts the arguments of Erdös, Särközy, and Sós. The reason can be explained as follows. The most natural way to generate a triple
, this strategy cannot work, as it contradicts the arguments of Erdös, Särközy, and Sós. The reason can be explained as follows. The most natural way to generate a triple  of random natural numbers in
of random natural numbers in 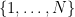 which multiply to a square is to set
which multiply to a square is to set

for some random natural numbers

. But if one wants all these numbers to have magnitude

, one sees on taking logarithms that one would need

which by elementary linear algebra forces

so in particular each of the

would have a factor comparable to
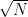
. However, it follows from known results on the “
multiplication table problem” (how many distinct integers are there in the
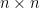
multiplication table?) that most numbers up to

do
not have a factor comparable to
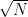
. (Quick proof: by the
Hardy–Ramanujan law, a typical number of size

or of size
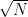
has

factors, hence typically a number of size

will not factor into two factors of size
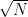
.) So the above strategy cannot work for
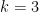
.
However, the situation changes for larger  . For instance, for
. For instance, for  , we can try the same strategy with the ansatz
, we can try the same strategy with the ansatz

Whereas before there were three (approximate) equations constraining three unknowns, now we would have four equations and six unknowns, and so we no longer have strong constraints on any of the

. So in principle we now have a chance to find a suitable random choice of the

. The most significant remaining obstacle is the Hardy–Ramanujan law: since the

typically have

prime factors, it is natural in this

case to choose each

to have

prime factors. As it turns out, if one does this (basically by requiring each prime

to divide

with an independent probability of about

, for some small
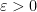
, and then also adding in one large prime to bring the magnitude of the

to be comparable to

), the calculations all work out, and one obtains the claimed result.
, let
be the size of the largest subset
of
with the property that no
distinct elements of
multiply to a square. In a paper by Erdös, Sárközy, and Sós, the following asymptotics were shown for fixed
:
.
.
.
for
.
for
.
for
.
of distinct random natural numbers in
which multiply to a square, and which are reasonably uniformly distributed throughout
, in that each individual number
is attained by one of the random variables
with a probability of
. If one can find such a distribution, then if the density of
is sufficienly close to
, it will happen with positive probability that each of the
will lie in
, giving the claim.
, this strategy cannot work, as it contradicts the arguments of Erdös, Särközy, and Sós. The reason can be explained as follows. The most natural way to generate a triple
of random natural numbers in
which multiply to a square is to set
. For instance, for
, we can try the same strategy with the ansatz

23 comments
Comments feed for this article
20 May, 2024 at 7:30 pm
Anonymous
Bravo!
20 May, 2024 at 7:53 pm
domotorp
See also https://arxiv.org/abs/2405.12088 which just appeared on arXiv.
20 May, 2024 at 8:08 pm
Terence Tao
Wow, that is quite a coincidence in timing! It seems the papers, while very adjacent in topic, do not actually overlap, but I will certainly update my paper to reference theirs.
21 May, 2024 at 9:04 am
Anonymous
That’s certainly amazing.
21 May, 2024 at 3:56 pm
Anonymous
Why the case of odd 𝑘 ≥ 5? see above
22 May, 2024 at 9:58 am
Terence Tao
I am not sure exactly what the thrust of your question is, but one can get significantly stronger upper bounds in the even case because one can exploit the birthday paradox: if one can find two separate -tuples in
-tuples in  whose products have the same square-free part, then the product of the entire
whose products have the same square-free part, then the product of the entire 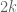 -tuple will be a square. One can use this trick to generate even tuples that multiply to a square, but not odd tuples. Similarly, it is easier to generate strong lower bounds in the odd case than in the even case, because the set of numbers that have an odd number of prime factors in a given set
-tuple will be a square. One can use this trick to generate even tuples that multiply to a square, but not odd tuples. Similarly, it is easier to generate strong lower bounds in the odd case than in the even case, because the set of numbers that have an odd number of prime factors in a given set 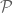 of primes, will necessarily have all odd products being a non-square, and all known counterexamples are based on this construction with a suitably optimized choice of
of primes, will necessarily have all odd products being a non-square, and all known counterexamples are based on this construction with a suitably optimized choice of 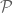 .
.
23 May, 2024 at 3:19 am
Will Sawin
Lovely!
If one were to make the upper bound on the density obtained by this method explicit, it would go to 1 with k. Indeed it couldn’t possibly be higher than 1-1/k since we need to lower bound the probability that a k-tuple of random variables lies in A based only on information in the marginal distribution, requiring us to use the union bound, which loses at least 1 minus the density for each element of the tuple.
Might it be possible to prove a bound uniform in k at least 5 by some modification of this method? It seems tricky as one would have to prove the events n_i in A approximately independent in some sense. But actually I’m not sure that this is the main obstacle – it’s possible the current bounds from an explicit version of your argument go to 1 significantly faster than this.
23 May, 2024 at 9:40 am
Terence Tao
It seems one can get a lower bound on the leading constant that is uniform in by leveraging the even
by leveraging the even  theory, which among other things tells us that any set of positive density will contain
theory, which among other things tells us that any set of positive density will contain  distinct elements multiplying to a square if
distinct elements multiplying to a square if  is fixed and even. So then if
is fixed and even. So then if  is odd, and
is odd, and  is a subset of
is a subset of  that has density close to
that has density close to  , then one can first locate a tuple of five elements multiplying to a square, delete those elements, and then locate a tuple of
, then one can first locate a tuple of five elements multiplying to a square, delete those elements, and then locate a tuple of  (which is an even number that is at least 4) elements that multiply to a square in the remaining set. (In the notation of the paper, this argument shows that
(which is an even number that is at least 4) elements that multiply to a square in the remaining set. (In the notation of the paper, this argument shows that  for any fixed
for any fixed 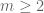 .) I’ll add this as a remark to the paper.
.) I’ll add this as a remark to the paper.
25 May, 2024 at 12:17 am
Csaba Sandor
Let be a positive integer. Then
be a positive integer. Then  . Let
. Let  be a largest subset of
be a largest subset of ![[1,N]](https://s0.wp.com/latex.php?latex=%5B1%2CN%5D&bg=ffffff&fg=545454&s=0&c=20201002) that does not contain
that does not contain 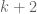 distinct elements whose product is a square. It is known that
distinct elements whose product is a square. It is known that  . Then one can locate elements
. Then one can locate elements  ,
,  multiplying to a square. Then
multiplying to a square. Then  is a set that does not contain
is a set that does not contain  distinct elements whose product is a square.
distinct elements whose product is a square.
25 May, 2024 at 7:06 am
Terence Tao
Nice! So now the monotonicity of for odd
for odd  is settled.
is settled.
3 June, 2024 at 2:27 am
Anonymous
can you add it to your article (with ack. for Sandor of course)?
3 June, 2024 at 2:42 am
Anonymous
my bad, v2 already is there…
25 May, 2024 at 7:31 am
Terence Tao
One way to think about this phenomenon is that the set is not an “irreducible” set in some arithmetic geometry sense, but instead has multiple interesting “components”. In my paper I rely more or less exclusively on the component which has the parameterization
is not an “irreducible” set in some arithmetic geometry sense, but instead has multiple interesting “components”. In my paper I rely more or less exclusively on the component which has the parameterization  for some natural numbers
for some natural numbers  with
with  . But there are other components as well; for instance one can retain this sort of parameterization just for
. But there are other components as well; for instance one can retain this sort of parameterization just for  , but have an unrelated parameterization
, but have an unrelated parameterization  ,
,  for the final two components; this is related to the monotonicity of
for the final two components; this is related to the monotonicity of 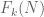 for odd
for odd  discussed previously. It is not clear a priori which components give the strongest bounds on
discussed previously. It is not clear a priori which components give the strongest bounds on 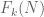 (and perhaps the best bounds could even come from a synergy between multiple components, rather than just taking the best bound provided by a single component).
(and perhaps the best bounds could even come from a synergy between multiple components, rather than just taking the best bound provided by a single component).
25 May, 2024 at 8:22 am
Terence Tao
As an experiment, I asked ChatGPT to provide Python code to compute the function , defined as the size of the largest subset of
, defined as the size of the largest subset of  with no odd number of them multiplying to a square. This is a lower bound for all the
with no odd number of them multiplying to a square. This is a lower bound for all the 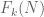 for odd
for odd  ; the quantity
; the quantity  is also the minimal size of
is also the minimal size of  where
where  ranges over
ranges over  -valued completely multiplicative functions. As it turned out the code ran flawlessly (other than I had to figure out install the sympy package, and how to print the results), and only took me a few minutes to complete: https://chatgpt.com/share/e021a5fb-5040-427b-a1a8-260fb31eeb08 . On consulting the OEIS, I found that the sequence
-valued completely multiplicative functions. As it turned out the code ran flawlessly (other than I had to figure out install the sympy package, and how to print the results), and only took me a few minutes to complete: https://chatgpt.com/share/e021a5fb-5040-427b-a1a8-260fb31eeb08 . On consulting the OEIS, I found that the sequence  already appears as https://oeis.org/A360659 (which also provided confirmation of the correctness of the GPT-provided code, which I also spot-checked with small values of
already appears as https://oeis.org/A360659 (which also provided confirmation of the correctness of the GPT-provided code, which I also spot-checked with small values of  ), although
), although  is not, but I just submitted it to the OEIS. (I haven’t tried the analogous exercise with the
is not, but I just submitted it to the OEIS. (I haven’t tried the analogous exercise with the 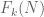 , which are harder to compute for
, which are harder to compute for  , but presumably one could get GPT to produce some algorithm that could produce enough entries to check the OEIS.)
, but presumably one could get GPT to produce some algorithm that could produce enough entries to check the OEIS.)
UPDATE: F(N) is now at https://oeis.org/A373114
25 May, 2024 at 9:55 am
Terence Tao
Indeed, ChatGPT could compute by brute force for
by brute force for  up to 10 in less than a minute: https://chatgpt.com/share/79ab37e7-d14d-4ae7-96d6-a5794a0a9581 . I could verify and extend the sequence by hand to
up to 10 in less than a minute: https://chatgpt.com/share/79ab37e7-d14d-4ae7-96d6-a5794a0a9581 . I could verify and extend the sequence by hand to
and it does not appear to be in the OEIS; I will add it after the sequence is approved (this is currently in process). [
is approved (this is currently in process). [ and
and  already appear in the OEIS as https://oeis.org/A028391 and https://oeis.org/A013928 respectively.]
already appear in the OEIS as https://oeis.org/A028391 and https://oeis.org/A013928 respectively.]
UPDATE: is now at https://oeis.org/A372306.
is now at https://oeis.org/A372306.  is at https://oeis.org/A373119,
is at https://oeis.org/A373119,  is at https://oeis.org/A373178, and
is at https://oeis.org/A373178, and  is at https://oeis.org/A373195.
is at https://oeis.org/A373195.
25 May, 2024 at 3:55 pm
Anonymous
has the oeis led to discoveries?
26 May, 2024 at 3:57 pm
Terence Tao
There are over 10,000 research papers that cite the OEIS, so I presume some non-trivial fraction of these found it useful.
30 May, 2024 at 1:58 pm
Anonymous
Are there similar results for representations of cubes?
[Yes; see the paper https://arxiv.org/abs/2405.12088 referenced in a previous comment -T.]
9 June, 2024 at 3:57 am
Anonymous
Is it possible to show that the sequence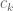 is monotonic?
is monotonic?
14 June, 2024 at 2:41 pm
Anonymous
Yes.
14 June, 2024 at 3:16 pm
Terence Tao
The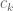 are known to equal 1 for even
are known to equal 1 for even  , and are at most
, and are at most  for odd
for odd  , so the sequence is not monotonic over the full natual numbers; however they are monotonic non-decreasing for odd
, so the sequence is not monotonic over the full natual numbers; however they are monotonic non-decreasing for odd  (see the comment of Sandor here).
(see the comment of Sandor here).