In the last few weeks, the Great Internet Mersenne Prime Search (GIMPS) announced the discovery of two new Mersenne primes, both over ten million digits in length, including one discovered by the computing team right here at UCLA (see this page for more information). [I was not involved in this computing effort.] As for the question “Why do we want to find such big primes anyway?”, see this page, though this is not the focus of my post today.
The GIMPS approach to finding Mersenne primes relies of course on modern computing power, parallelisation, and efficient programming, but the number-theoretic heart of it – aside from some basic optimisation tricks such as fast multiplication and preliminary sieving to eliminate some obviously non-prime Mersenne number candidates – is the Lucas-Lehmer primality test for Mersenne numbers, which is much faster for this special type of number than any known general-purpose (deterministic) primality test (such as, say, the AKS test). This test is easy enough to describe, and I will do so later in this post, and also has some short elementary proofs of correctness; but the proofs are sometimes presented in a way that involves pulling a lot of rabbits out of hats, giving the argument a magical feel rather than a natural one. In this post, I will try to explain the basic ideas that make the primality test work, seeking a proof which is perhaps less elementary and a little longer than some of the proofs in the literature, but is perhaps a bit better motivated.
— Order —
We begin with a general discussion of how to tell when a given number n (which is not necessarily of the Mersenne form ) is prime or not. One should think of n as being moderately large, e.g.
(which is broadly the size of the Mersenne primes discovered recently).
Our starting point will be Lagrange’s theorem, which asserts that
(1)
for any finite group G and any , thus the order
of a in G divides |G|. Specialising this to the multiplicative group
of a finite field of prime order p, we obtain Fermat’s little theorem
(2)
for prime and
coprime to
; applying it instead to the multiplicative group
of a cyclic group of order
, we obtain Euler’s theorem
(3)
whenever is coprime to n, where
is the Euler totient function of n.
Fermat’s little theorem (2) already gives a necessary condition for the primality of a candidate prime : take any
coprime to
(typically one picks a small number such as
or
), and compute
modulo
. If it is not equal to 1, then
cannot be prime. This is a (barely) feasible test to execute for
as large as
, because one can compute exponents such as
relatively quickly, by the trick of repeatedly squaring a modulo n to obtain
, and then decomposing
into binary to compute
. (If
is a Mersenne number, then there are some pretty obvious shortcuts one can take for this last step, using division instead of multiplication.) Unfortunately, while this test is necessary for primality, it is not sufficient, due to the existence of pseudoprimes. So Fermat’s little theorem alone does not provide the answer, at least if one wants a deterministic certificate of primality rather than a probabilistic one.
Nevertheless, the above facts do provide some important information about the order of a modulo
. If
is prime, Fermat’s little theorem (2) tells us that
is at most
(in fact, it divides
). On the other hand, if
is not prime, then Euler’s theorem (3) tells us that
cannot be as large as
, but is instead at most
, which is now strictly less than
. Thus: if we can find a number
coprime to
such that
is exactly
, we have certified that
is prime.
Testing whether a given number is coprime to
is very easy and fast (thanks to the Euclidean algorithm). Unfortunately, it is difficult in general to compute the order
of a number
if the base
is large; a brute-force approach would require one to compute up to
powers of
, which is prohibitively expensive if
has size comparable to
. (More generally, the problem of computing order exactly in general is closely related to the discrete logarithm problem, which is notoriously difficult.) However, there are a few cases in which the order can be found very quickly. Suppose that we somehow find positive integers
,
such that
(4)
(which in particular implies that is coprime to
). Squaring this, we obtain
and so we see that divides
but not
, and thus must be exactly equal to
. Conversely, if
, then we must have (4). So in the special case when the order of
is a power of 2, we can compute the order using only one exponentiation, which is computationally feasible for the orders of magnitude we are considering.
Unfortunately, this is not quite what we need for the Mersenne prime problem, because if is a Mersenne number, then it is
plus 1 which is a power of 2, rather than
minus 1. (The above method would be ideal for finding Fermat primes rather than Mersenne primes, but it is likely that in fact there are no more such primes to be found.)
So this is a frustrating near miss: if is a Mersenne number, we can easily check if a number has order
modulo
, but we needed a test for when a number has order
instead. And indeed, even when
is prime, Fermat’s little theorem (2) shows that it is impossible for a number to have order
modulo
, since the order needs to divide
. So we seem to be a bit stuck.
But while clearly does not divide
, it does divide
. Looking at Lagrange’s theorem (1), we then see that it could be possible to find elements of order
in a multiplicative group of order
rather than
. Recall that if
was prime, then the multiplicative group
of the finite field
had order
. But
is also a finite field, and its multiplicative group
has order
. Aha!
So the plan (assuming for sake of argument that is prime) is to somehow work in the finite field
instead of
, in order to find elements of order
. We can get our hands on this larger finite field more concretely by viewing it as a quadratic extension
, where a is a quadratic non-residue of
.
Let’s now take n to be a Mersenne prime. What numbers are quadratic non-residues? A quick appeal to quadratic reciprocity and some elementary number theory soon reveals that 2 is a quadratic residue of , but that 3 is not. Thus we can take
. (One could work with other numbers than 3 here, but being the smallest quadratic non-residue available, it is the simplest one to use, and the one which is most likely to be able to take advantage of the strong law of small numbers.) Henceforth all calculations will be in this field
, which of course contains
as a subfield.
Now we need to look for a field element of order
, which is a power of 2. Thus (by adapting (4) to
) we need to find a solution to the equation
(5)
in this field.
Let’s compute some expressions of the form . From Fermat’s little theorem (2) we have
;
because 3 is not a quadratic residue, we see (from taking discrete logarithms) that
(6)
and thus
.
Similarly we have
(7).
These are pretty close to (5), but not quite right. To go further, it is convenient to work with powers rather than
powers – i.e. we work with the Frobenius automorphism
. Indeed, since
has characteristic n, we have the automorphism properties
;
. (8)
From (6) we have , while from (2) we have
for
. From (8) we thus see that
for ; thus the Frobenius automorphism is nothing more than Galois conjugation. (Actually, this can be deduced quite readily from standard Galois theory.)
Now we go back from powers to
powers. Multiplying both sides of the preceding equation by
, we obtain
.
Squaring , we conclude
.
Now we in a good position to solve the equation (5). We cannot make equal to -1 – since -1 is not a quadratic residue modulo 3 – but we can make it equal to, say, -2, by setting a=1 and b=-1 (say):
.
Dividing this by (7) we obtain the desired solution
(9)
to (5), where . (Note that one could also use
here; indeed, Galois theory tells us that
and
are interchangeable in these computations.)
To summarise, we have shown that
If is a Mersenne prime, then (9) holds.
Based on our previous discussion, we expect to be able to reverse this implication. Indeed, we have the following converse:
Lemma 1. Let
be a Mersenne number. If (9) holds (in the ring
), then
is prime.
Proof. Let be a prime divisor of
. Then
in the field
(which we define as
if 3 is a quadratic residue there), thus
has order exactly n+1 (cf. (4)). By Lagrange’s theorem (1), this means that
divides the multiplicative order of
, which is
(if 3 is a non-residue modulo
) or
(if 3 is a residue modulo
). In particular,
has to exceed
. Thus the only prime divisors of
exceed
, and so by the sieve of Eratosthenes,
is prime. (This proof is due to Bruce.)
We have thus shown
Corollary 1. (Lucas-Lehmer test, preliminary version) Let
with m odd. Then n is prime if and only if (9) holds in
.
This is already a reasonable criterion, but it is a little non-elementary (and also a little unpleasant numerically) due to the presence of the quadratic extension by . One can get rid of this extension by the Galois theory trick of taking traces. Indeed, observe that
is the Galois conjugate of
. Basic Galois theory tells us that
lies in
, and vanishes precisely when
is equal to -1. So it suffices to show that
vanishes in .
The quantity could be computed by repeated squaring in
. The quantity
can be computed by a similar device in
. Indeed, the sequence
is easily seen to obey the recursion
(10)
and so we have
Theorem 1. (Lucas-Lehmer test, final version) Let
with m odd. Then n is prime if and only if
vanishes modulo n, where
is given by the recursion (10).
To apply this test, one needs to perform about squaring operations modulo
. Doing everything as efficiently as possible (in particular, using fast multiplication), the total cost of testing a single Mersenne number
for primality is about
(modulo some
terms). This turns out to barely be within reach of modern computers for
, especially since the algorithm is somewhat parallelisable. (In contrast, the best known general-purpose deterministic primality testing algorithm, the AKS algorithm, has a run time of about
(with a sizable implicit constant), which is not feasible for
.) There are general-purpose probabilistic tests (such as Miller-Rabin) which have run-time comparable to the Lucas-Lehmer test, but as mentioned at the beginning, we are only interested here in deterministic (and unconditional, e.g. not relying on GRH) certificates of primality.
[Updated, Nov 16: Lemma 1 corrected.]

26 comments
Comments feed for this article
2 October, 2008 at 9:43 am
Prime Numbers: Mersenne Primes Edition « OU Math Club
[…] used by the GIMPS project to test if a Mersenne number is actually prime. You can check it out here. Note: UCLA computers were used to find one of the new […]
2 October, 2008 at 10:33 am
Anonymous
I think there is a typo in the third paragraph, in the phrase: “prime our not.”
2 October, 2008 at 10:44 am
Terence Tao
Thanks for the correction!
3 October, 2008 at 12:21 am
François Brunault
Thank you for this nice exposition! I should add that B. H. Gross recently devised a beautiful primality test for Mersenne numbers which is based on elliptic curves. The idea is to replace the multiplicative group of a finite field by the group of points of a suitable elliptic curve E over F_p. Here E is given by the Weierstrass equation y^2 = x^3 – 12x. This elliptic curve has complex multiplication, which makes the group of points over F_p easier to compute. It turns out that if p is a Mersenne prime then this group is cyclic of order p+1, which is exactly what one wants. Then successive squaring is replaced by the duplication map on the elliptic curve. Unfortunately, the formula for the duplication map on an elliptic curve is more complicated, so this test seems to be mainly interesting from a theoretical point of view.
3 October, 2008 at 6:28 am
Anonymous
Dear Prof. Tao,
Thank you for another interesting post. This is the clearest exposition of the Lucas-Lehmer test I have read. I think there is a typo about 8 lines after formula (8). In the formula following “Squaring a+b\sqrt{3}…” should be (a^2+3b^2+2ab\sqrt{3})…. Also 2 lines after that a^2-3b^2 instead of a^2=3b^2.
Also of couse in looking for Mersenne prime, one needs only consider Mersenne number n=2^m-1, where m is prime since 2^a-1 divides
2^(ab)-1. [Corrected – T.]
3 October, 2008 at 1:16 pm
Anonymous
Thanks for a very enjoyable read. A very minor correction: in the sentence beginning “We cannot make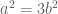 equal to
equal to  ,” I think you mean
,” I think you mean 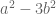 . [Corrected – T.]
. [Corrected – T.]
6 October, 2008 at 2:44 am
david
Very happy to visit you blog, young hero!
6 October, 2008 at 11:06 am
Jernej
Hello, I think there’s a small mistake in the text :
===
Fermat’s little theorem (2) already gives a necessary condition for the primality of a candidate prime : take any a coprime to n (typically one picks a small number such as a = 2 or a = 3 ), and compute a^{n-1} modulo n . If it is not equal to 1, then p cannot be prime.
===
You probably meant n instead of p.
6 October, 2008 at 11:20 am
Terence Tao
Dear Jernej: thanks for the correction!
7 October, 2008 at 2:54 am
Anonymous
Thank you for your beautiful exposition.
Another tiny misprint. In the statement Fermat’s little theorem, the “a” in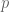 prime and a coprime to
prime and a coprime to 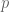
==
for
==
should be in math mode. [Corrected – T.]
8 October, 2008 at 7:53 pm
Anonymous
Great explanation!
As another possible justification for why people are searching for larger mersenne primes, there’s a clever construction of Locally Decodable Codes by Yekhanin that works in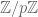 where
where 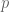 is a Mersenne prime. Since his bounds get better as
is a Mersenne prime. Since his bounds get better as 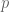 increases, he specifically cites the (then) largest Mersenne prime in his bounds.
increases, he specifically cites the (then) largest Mersenne prime in his bounds.
http://portal.acm.org/citation.cfm?id=1250830#
25 October, 2008 at 10:17 pm
Jaime Montuerto
Dear Terry,
Your posts on Mersenne Numbers and your following post about Galois groups and the order in the group gave me several insights for my proposed hypothesis. This hypothesis is that every prime number (in fact all integers) divide a Mersenne number. It is also true that every Mersenne number is a multiple of a prime and sometimes some Mersennes have more prime divisors.
One of the consequences of this is that the number of primes is almost equal to the number of Mersenne numbers. Almost equal because some Mersennes give off two primes and these Mersennes are those that have prime orders and themselves are composite e.g. M11, M23, and M47. And possibly some Mersennes whose order is a square e.g. M25 = 601 * 1801 * 31, both 601 and 1801 divides M25 as minimum Mersenne whereas 31 divides M5 (which is itself) therefore not the prime in question. There are almost an equal number of Mersennes and primes, primes are a bit more over some given range.
A further consequence is that there are infinite Mersennes, that is, for every integer there is corresponding Mersenne i.e. integer n means Mn therefore a new prime that divides that. Hence there are infinite primes.
Another consequence is that the distribution of Mersennes is a recurrence relation, Mnext = Mprevious *2 + 1, i.e. the present Mersennne is almost double the previous one. Therefore the ordering of Mersenne is so predictable and almost so ordered, given a range ‘n’ the number of Mersennes in that range is ‘log n’ on base 2. Then the number of primes in that range is also ‘log n’ almost. I believed this is what Friedrick Gauss has observed in the distribution of primes.
I am developing two major areas of research in factoring Mersennes:
(1) Following your post about discrete logarithms I realized that the first algorithm is exactly based on that – it looks for 2^x where the remainder is 1 modulo n or looking for a pair of 2^x and 2^y where there remainder is the same hence the cycle is a difference of x and y, the difference is actually either a multiple, equal or a fraction of this cycle.
(2) The other algorithm is base on the grammar of partitions. A good metaphor I used is the monetary system, as, some reason, almost everyone can calculate when money is involved. Imagine all notes or bills are doubles of the previous one. The smallest is a dollar ‘1’, next is 2 dollars, and so on – essentially the binary system. The question is, given a certain amount, can we break/partition the bills in such a way that the relationship of each adjacent bills (binary bits) forms a set of predefined law (grammatical laws)? The essence of these is that if a sentence (grammatical sentence) is formed or produced by these laws then we can find the factors of that amount. Prime number amounts do not produce well-formed sentences.
It is very hard to explain all the details of what I am doing. I only hope that it is clear enough for you to be able to understand a little of my work. There is of course much more that could be said about this.
I would be very grateful for any comments you could make.
Thanking you in anticipation.
Best
Jaime Montuerto
16 November, 2008 at 2:17 am
Rene' Schoof
Dear Prof. Tao,
I have a question about the proof of
your Lemma 1. You seem to assume that under the conditions
of the lemma, automatically 3 is a non-square modulo q for
any prime divisor q of n.
How do you see that?
Best
Rene’ Schoof
17 November, 2008 at 2:56 am
Terence Tao
Dear Rene’,
Thanks for pointing that out! Actually, it turns out that the argument works just as well when 3 is a square modulo q (one simply replaces![F_q[\sqrt(3)]](https://s0.wp.com/latex.php?latex=F_q%5B%5Csqrt%283%29%5D&bg=ffffff&fg=545454&s=0&c=20201002) with
with  in this case). I’ve modified the discussion to reflect this.
in this case). I’ve modified the discussion to reflect this.
12 December, 2008 at 12:31 am
Tarandeep Singh
Dear Professor Tao,
I was working on the Mersenne primes and it appears there is “some pattern” in all the known Mersenne primes. I have verified it for the 46 known Mersenne Primes and it holds.
I am not sure if its something “easily provable” or we do have something that has gone unnoticed before.
Need to know if you would be interested to see the pattern/conjecture and comment on the same.
Thanks in advance.
Tarandeep Singh
6 January, 2009 at 12:54 pm
Tony Reix
Hi Sir,
Thanks for the proof. I’ll study it and see if it can help me.
I’m one of the crazy guys who contribute to the GIMPS project, since ages.
I’ve contributed to checking the last 6 Mersenne primes, on a big Itanium2 machine, with the wonderful Glucas program written by Guillermo Ballester Valor.
I also spent a lot of time studying the LLT, reading E. Lucas books, HC Williams book about E. Lucas work, Ribenboim famous book about primes, and so on.
I’ve also found some properties of Mersenne numbers and of the LLT, with proof of myself or by other people. Mq=(8x)^2-(3qy)^2. As an example for LLT, since it is not well known that the LLT can be used to prove that a Fermat number is prime (a number N such that N-1 is easily factorized), I wrote such a proof, based on Ribenboim technic and on Williams’ book.
So, though I am an “amateur”, I have some knowledge of the LLT test.
The LLT test makes use of the tree that appears in the DiGraph under x^2-2 modulo a Mersenne prime (see Shallit & Vasiga for details). This DiGraph also has many cycles, of lengh dividing q-1. I found the formula that gives the number of cycles of lengh L, under x^2 and x^2-2 modulo a Mersenne prime. Someone else built the proof.
I also have conjectured a test that makes use of such a cycle of length q-1 (with a fix seed) instead of the tree (with seed 4). The main difference with the basic LLT test is that the last step of the iteration, instead of leading to 0 (mod Mq), leads to the seed of the iteration: S_0. Thanks to some help of Mr Williams, I’ve been able to prove that, if Mq is prime, then the property holds. But I failed finding a way to prove the reverse…
In short, the x^2-2 builds trees and cycles modulo a number. If the number is prime, there is symmetry. If the number is composite, then trees and cycles are not symmetric. My idea is that cycles can be used as the tree is used for proving that a number is prime.
This would not be very interesting to have another test for Mersenne numbers, since it would not be faster than LLT.
But Anton Vrba built a conjecture about using the same technique for a primality proof for Fermat 2^2^n+1 and Wagstaff (2^q+1)/3 numbers. And he provided a proof for the first (easy) part: a Prime number HAS this property.
About Wagstaff numbers, proving the conjecture would lead to a brand new primality test as efficient as the LLT is for Mersenne numbers. That would be the first VERY efficient test for a number not N-1 nor N+1. But Anton failed to prove the reverse… Some Mathematician contributing to the GIMPS Math forum think that, though it should be possible for the Mersenne, it does not seem possible to prove the conjecture for Wagstaffs. However, the DiGraph under x^2-2 modulo a Wagstaff prime only has cycles. No tree.
About Fermat numbers (tree and cycles), I guess (just a guess…) that it could be possible to build a test that could be used to prove that a Fermat number is NOT prime, much faster than running the full Pépin’s test. This could be possible since the Digraph under x^2-2 modulo a Fermat prime generates cycles of length dividing 2^n-1. I expect that a Fermat number that does not verify such a (much shorter) test could not be a prime. Just an idea… but it could help to know what is the status of F33.
So, there is here an area of research. Simply studying the properties of the cyles and trees for the Mersenne, Fermat and Wagstaff numbers under x^2 or x^2-2 would be very interesting, and useful for further reseach. It could be the subject of a study for a Math student (too hard for me…).
Succeeding in proving the conjectures would be a great success !
If you are interested by this subject, just contact me at
tony . reix @ laposte . net .
Regards,
Tony
11 August, 2009 at 11:50 am
The AKS primality test « What’s new
[…] numbers. (The situation improves though for more special types of , such as Mersenne numbers; see my earlier post on the Lucas-Lehmer test for more […]
29 November, 2009 at 12:56 pm
trex58
OK.
Look at: http://tony.reix.free.fr/Mersenne/SummaryOfThe3Conjectures.pdf
and: http://trex58.wordpress.com/math2matiques/
for more information.
Tony
28 February, 2010 at 3:25 pm
trex58
Thanks to the Vrba-Reix conjecture based on the ideas I talked previously in this page, and thanks to the version 3.8.0 of LLR by Jean Penné, I’ve been able to find a new Wagstaff PRP : (2^4031399+1)/3 , which is today the 3rd biggest PRP number ever found, with 1,213,572 digits. With a proof of Vrba’s conjecture, it would turn into a prime, the 22th biggest one.
See: http://www.primenumbers.net/prptop/prptop.php?page=1#haut
Regards,
Tony Reix
21 March, 2011 at 11:57 am
Guntram Hainke
I think one can even do with less magic than in the text. Suppose that $q=2^n-1$ is a Mersenne prime.
Consider the field $F=F_{q^2}$ and recall that there is a homomorphism $n: F^\times \to F_q$ given by $N(x)=x\cdot x^q$, the norm. Let $N$ denote the kernel of this homomorphism, i.e. the subgroup of elements of norm 1.
Then $N$ has order $p+1$ and is cyclic as it is a finite subgroup of the multiplicative group of a field.
The magic of the Lucas-Lehmer test is that $2+\sqrt{3}$ is a generator for this group, regardless of which Mersenne prime we consider.
But let me stress that the fact that there is such an element (of norm 1) follows from general theory.
28 November, 2013 at 1:20 pm
Two applications of finite fields to computational number theory | Matt Baker's Math Blog
[…] is due to Michael Rosen, with simplifications by J.W. Bruce. Our exposition was influenced by this blog post written by Terry Tao, which the interested reader should definitely […]
26 September, 2014 at 4:12 am
My great WordPress blog – Econlinks
[…] are interested in finding prime numbers with tens of millions of digits. And a nice exposition of the Lucas-Lehmer test for Mersenne primes by Terry Tao, to whom I owe also the previous […]
11 January, 2018 at 8:12 am
Andy Rocketman
Dear Prof. Tao,
I don’t know if this is even a proper question, but:
The LL test with starting values of 4 generates an accompanying sequence of Heronian triangles, as in: [13,14,15],[193,194,195],[37633,37634,37635]
The second to last and final LL residual sometimes have an accompanying Pythagorean triple (depending on the Lehmer symbol), as in: [15,112,113],[511,130560,130561],[1023,523264,523265]
Does this suggest some geometric analogy underlying the test that involves triangles?
Sorry if this is a silly question!
Andy
2 December, 2022 at 3:06 am
LUIS MARTINEZ
Mersenne Primes Problem Solved (Enfer Diez)
That is to say, to know which Mersenne number is prime (without the factorization), ieasy to verify with the known primes and, in turn; determine new primes whatever the digit number.
If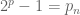 is a Mersenne prime we will have:
is a Mersenne prime we will have:
If![3p - 1 = \frac{3[4x+1] + 1}{5}](https://s0.wp.com/latex.php?latex=3p+-+1+%3D+%5Cfrac%7B3%5B4x%2B1%5D+%2B+1%7D%7B5%7D&bg=ffffff&fg=545454&s=0&c=20201002)
Then:![p_{n} + 1 = \frac{3[4x+1] + 1}{5} = 2^{p}](https://s0.wp.com/latex.php?latex=p_%7Bn%7D+%2B+1+%3D+%5Cfrac%7B3%5B4x%2B1%5D+%2B+1%7D%7B5%7D+%3D+2%5E%7Bp%7D&bg=ffffff&fg=545454&s=0&c=20201002) .
.
Examples
15 December, 2022 at 9:35 am
Luis martinez
For those interested in the Mersenne primes and in the of Enfer method; (x) always follows a pattern: