Let be a natural number. A basic operation in the topology of oriented, connected, compact,
-dimensional manifolds (hereby referred to simply as manifolds for short) is that of connected sum: given two manifolds
, the connected sum
is formed by removing a small ball from each manifold and then gluing the boundary together (in the orientation-preserving manner). This gives another oriented, connected, compact manifold, and the exact nature of the balls removed and their gluing is not relevant for topological purposes (any two such procedures give homeomorphic manifolds). It is easy to see that this operation is associative and commutative up to homeomorphism, thus
and
, where we use
to denote the assertion that
is homeomorphic to
.
(It is important that the orientation is preserved; if, for instance, , and
is a chiral 3-manifold which is chiral (thus
, where
is the orientation reversal of
), then the connect sum
of
with itself is also chiral (by the prime decomposition; in fact one does not even need the irreducibility hypothesis for this claim), but
is not. A typical example of an irreducible chiral manifold is the complement of a trefoil knot. Thanks to Danny Calegari for this example.)
The -dimensional sphere
is an identity (up to homeomorphism) of connect sum:
for any
. A basic result in the subject is that the sphere is itself irreducible:
For (curves), this theorem is trivial because the only connected
-manifolds are homeomorphic to circles. For
(surfaces), the theorem is also easy by considering the genus of
. For
the result follows from the prime decomposition. But for higher
, these ad hoc methods no longer work. Nevertheless, there is an elegant proof of Theorem 1, due to Mazur, and known as Mazur’s swindle. The reason for this name should become clear when one sees the proof, which I reproduce below.
Suppose . Now consider the infinite connected sum
This is an infinite connected sum of spheres, and can thus be viewed as a half-open cylinder, which is topologically equivalent to a sphere with a small ball removed; alternatively, one can contract the boundary at infinity to a point to recover the sphere . On the other hand, by using the associativity of connected sum (which will still work for the infinite connected sum, if one thinks about it carefully), the above manifold is also homeomorphic to
which is the connected sum of with an infinite sequence of spheres, or equivalently
with a small ball removed. Contracting the small balls to a point, we conclude that
, and a similar argument gives
.
A typical corollary of Theorem 1 is a generalisation of the Jordan curve theorem: any locally flat embedded copy of in
divides the sphere
into two regions homeomorphic to balls
. (Some sort of regularity hypothesis, such as local flatness, is essential, thanks to the counterexample of the Alexander horned sphere. If one assumes smoothness instead of local flatness, the problem is known as the Schönflies problem, and is apparently quite subtle, especially in the four-dimensional case
.)
One can ask whether there is a way to prove Theorem 1 for general without recourse to the infinite sum swindle. I do not know the complete answer to this, but some evidence against this hope can be seen by noting that if one works in the smooth category instead of the topological category (i.e. working with smooth manifolds, and only equating manifolds that are diffeomorphic, and not merely homeomorphic), then the exotic spheres in five and higher dimensions provide a counterexample to the smooth version of Theorem 1: it is possible to find two exotic spheres whose connected sum is diffeomorphic to the standard sphere. (Indeed, in five and higher dimensions, the exotic sphere structures on
form a finite abelian group under connect sum, with the standard sphere being the identity element. The situation in four dimensions is much less well understood.) The problem with the swindle here is that the homeomorphism generated by the infinite number of applications of the associativity law is not smooth when one identifies the boundary with a point.
The basic idea of the swindle – grouping an alternating infinite sum in two different ways – also appears in a few other contexts. Most classically, it is used to show that the sum does not converge in any sense which is consistent with the infinite associative law, since this would then imply that
; indeed, one can view the swindle as a dichotomy between the infinite associative law and the presence of non-trivial cancellation. (In the topological manifold category, one has the former but not the latter, whereas in the case of
, one has the latter but not the former.) The alternating series test can also be viewed as a variant of the swindle.
Another variant of the swindle arises in the proof of the Cantor–Bernstein–Schröder theorem. Suppose one has two sets , together with injections from
to
and from
to
. The first injection leads to an identification
for some set
, while the second injection leads to an identification
. Iterating this leads to identifications
and
for some additional set . Using the identification
then yields an explicit bijection between
and
.
(Thanks to Danny Calegari for telling me about the swindle, while we were both waiting to catch an airplane.)
[Update, Oct 7: See the comments for several further examples of swindle-type arguments.]

14 comments
Comments feed for this article
5 October, 2009 at 11:38 pm
Scott Morrison
Another nice application is to show that non-trivial knots don’t have inverses under connect sum: you can’t untie a knot by tying another one!
6 October, 2009 at 12:07 am
Jan
Nice explanation. Slight nitpick about the exotic spheres: if you happen to have an example of an exotic 4-sphere, you should write an article about it ;) Also, for the exotic 4-spheres it is not known whether they form a group under connected sums, only a monoid. Though of course, it could happen to be a group after all. [Fair enough; I’ve amended the relevant comment to refer only to exotic spheres of dimension five or more. -T]
6 October, 2009 at 12:23 am
Anonymous
I wasn’t previously familiar with the term “chiral manifold”, but I assume there is a there a typo in the first sentence of the second paragraph (“A chiral manifold which is chiral”). [Oops, the first “chiral” should have been “irreducible” – T.] Interesting post!
6 October, 2009 at 7:25 am
Qiaochu Yuan
Another example: if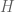 is an infinite-dimensional separable Hilbert space, then
is an infinite-dimensional separable Hilbert space, then  is contractible. The proof I know uses the identifications
is contractible. The proof I know uses the identifications  and it’s those identifications that allow an infinite sum to be regrouped.
and it’s those identifications that allow an infinite sum to be regrouped.
6 October, 2009 at 12:01 pm
toomuchcoffeeman
By GL(H) do you mean bounded linear invertible operators? in which case, contractibility would also follow from the fact that every invertible bounded operator is a product of two exponentials.
I dimly recall seeing something like what you mention in a textbook on K-theory, under the name of “Eilenberg swindle”.
6 October, 2009 at 12:13 pm
toomuchcoffeeman
Ah, I see from a comment below that I’ve misremembered about the Eilenberg trick/swindle. Apologies
6 October, 2009 at 10:15 am
Andy P.
A very amusing “appreciation” of Mazur’s swindle is contained in the introduction to Stallings’s talk at Mazur’s birthday conference, which is available here : http://math.berkeley.edu/~stall/mazur.html
6 October, 2009 at 11:58 am
Pace Nielsen
This reminds me of “Eilenberg’s Trick” from ring theory: If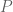 is projective, there is a free module
is projective, there is a free module  with
with 
The idea is to fix a module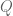 with
with  free, next set
free, next set  , and rearrange infinite sums in the right way.
, and rearrange infinite sums in the right way.
P.S. I hope I got the LaTeX code right. You might consider a “preview post” option.
6 October, 2009 at 12:08 pm
Peter
Small typo: in the Schroder-Bernstein example, the deductions of the identifications from the injections should be the other way round – i.e. the first injection gives , the second gives
, the second gives  . [Corrected, thanks – T.]
. [Corrected, thanks – T.]
7 October, 2009 at 12:53 pm
gowers
Pelczynski’s decomposition method is a nice trick in Banach spaces that makes use of a very similar idea. (No time to explain, but if you Google it you’ll see what I mean.)
7 October, 2009 at 4:12 pm
Jonathan Vos Post
http://www.springerlink.com/content/r3u0m800k5875312/fulltext.pdf?page=1
Generalizations of Pelczynski’s decomposition method for Banach
spaces containing a complemented copy of their squares
El´oi Medina Galego
Abstract. Suppose that X and Y are Banach spaces isomorphic to
complemented subspaces of each other. In 1996, W. T. Gowers solved the
Schroeder-Bernstein Problem for Banach spaces by showing that X is not
necessarily isomorphic to Y . However…
12 October, 2009 at 8:48 am
some guy on the street
I rather find the Banach-Tarski proof has a lot of swindle to it. When you think of running their oracle backwards, you might feel swindled again!
26 December, 2009 at 4:25 pm
A demonstration of the non-commutativity of the English language « What’s new
[…] the English language is non-commutative (or perhaps non-associative); a linguistic analogue of the swindle, if you […]
22 November, 2016 at 8:40 pm
An integration approach to the Toeplitz square peg problem | What's new
[…] In contrast to Conjecture 1, which is known for polygonal paths, Conjecture 2 is still open even under the hypothesis of polygonal paths; the homological arguments alluded to previously now show that the number of inscribed squares in the periodic setting is even rather than odd, which is not enough to conclude the conjecture. (This flipping of parity from odd to even due to an infinite amount of oscillation is reminiscent of the “Eilenberg-Mazur swindle“, discussed in this previous post.) […]