One of the major activities in probability theory is studying the various statistics that can be produced from a complex system with many components. One of the simplest possible systems one can consider is a finite sequence or an infinite sequence
of jointly independent scalar random variables, with the case when the
are also identically distributed (i.e. the
are iid) being a model case of particular interest. (In some cases one may consider a triangular array
of scalar random variables, rather than a finite or infinite sequence.) There are many statistics of such sequences that one can study, but one of the most basic such statistics are the partial sums
The first fundamental result about these sums is the law of large numbers (or LLN for short), which comes in two formulations, weak (WLLN) and strong (SLLN). To state these laws, we first must define the notion of convergence in probability.
Definition 1 Let
be a sequence of random variables taking values in a separable metric space
(e.g. the
could be scalar random variables, taking values in
or
), and let
be another random variable taking values in
. We say that
converges in probability to
if, for every radius
, one has
as
. Thus, if
are scalar, we have
converging to
in probability if
as
for any given
.
The measure-theoretic analogue of convergence in probability is convergence in measure.
It is instructive to compare the notion of convergence in probability with almost sure convergence. it is easy to see that converges almost surely to
if and only if, for every radius
, one has
as
; thus, roughly speaking, convergence in probability is good for controlling how a single random variable
is close to its putative limiting value
, while almost sure convergence is good for controlling how the entire tail
of a sequence of random variables is close to its putative limit
.
We have the following easy relationships between convergence in probability and almost sure convergence:
Exercise 2 Let
be a sequence of scalar random variables, and let
be another scalar random variable.
- (i) If
almost surely, show that
in probability. Give a counterexample to show that the converse does not necessarily hold.
- (ii) Suppose that
for all
. Show that
almost surely. Give a counterexample to show that the converse does not necessarily hold.
- (iii) If
in probability, show that there is a subsequence
of the
such that
almost surely.
- (iv) If
are absolutely integrable and
as
, show that
in probability. Give a counterexample to show that the converse does not necessarily hold.
- (v) (Urysohn subsequence principle) Suppose that every subsequence
of
has a further subsequence
that converges to
in probability. Show that
also converges to
in probability.
- (vi) Does the Urysohn subsequence principle still hold if “in probability” is replaced with “almost surely” throughout?
- (vii) If
converges in probability to
, and
or
is continuous, show that
converges in probability to
. More generally, if for each
,
is a sequence of scalar random variables that converge in probability to
, and
or
is continuous, show that
converges in probability to
. (Thus, for instance, if
and
converge in probability to
and
respectively, then
and
converge in probability to
and
respectively.
- (viii) (Fatou’s lemma for convergence in probability) If
are non-negative and converge in probability to
, show that
.
- (ix) (Dominated convergence in probability) If
converge in probability to
, and one almost surely has
for all
and some absolutely integrable
, show that
converges to
.
Exercise 3 Let
be a sequence of scalar random variables converging in probability to another random variable
.
- (i) Suppose that there is a random variable
which is independent of
for each individual
. Show that
is also independent of
.
- (ii) Suppose that the
are jointly independent. Show that
is almost surely constant (i.e. there is a deterministic scalar
such that
almost surely).
We can now state the weak and strong law of large numbers, in the model case of iid random variables.
Theorem 4 (Law of large numbers, model case) Let
be an iid sequence of copies of an absolutely integrable random variable
(thus the
are independent and all have the same distribution as
). Write
, and for each natural number
, let
denote the random variable
.
- (i) (Weak law of large numbers) The random variables
converge in probability to
.
- (ii) (Strong law of large numbers) The random variables
converge almost surely to
.
Informally: if are iid with mean
, then
for
large. Clearly the strong law of large numbers implies the weak law, but the weak law is easier to prove (and has somewhat better quantitative estimates). There are several variants of the law of large numbers, for instance when one drops the hypothesis of identical distribution, or when the random variable
is not absolutely integrable, or if one seeks more quantitative bounds on the rate of convergence; we will discuss some of these variants below the fold.
It is instructive to compare the law of large numbers with what one can obtain from the Kolmogorov zero-one law, discussed in Notes 2. Observe that if the are real-valued, then the limit superior
and
are tail random variables in the sense that they are not affected if one changes finitely many of the
; in particular, events such as
are tail events for any
. From this and the zero-one law we see that there must exist deterministic quantities
such that
and
almost surely. The strong law of large numbers can then be viewed as the assertion that
when
is absolutely integrable. On the other hand, the zero-one law argument does not require absolute integrability (and one can replace the denominator
by other functions of
that go to infinity as
).
The law of large numbers asserts, roughly speaking, that the theoretical expectation of a random variable
can be approximated by taking a large number of independent samples
of
and then forming the empirical mean
. This ability to approximate the theoretical statistics of a probability distribution through empirical data is one of the basic starting points for mathematical statistics, though this is not the focus of the course here. The tendency of statistics such as
to cluster closely around their mean value
is the simplest instance of the concentration of measure phenomenon, which is of tremendous significance not only within probability, but also in applications of probability to disciplines such as statistics, theoretical computer science, combinatorics, random matrix theory and high dimensional geometry. We will not discuss these topics much in this course, but see this previous blog post for some further discussion.
There are several ways to prove the law of large numbers (in both forms). One basic strategy is to use the moment method – controlling statistics such as by computing moments such as the mean
, variance
, or higher moments such as
for
. The joint independence of the
make such moments fairly easy to compute, requiring only some elementary combinatorics. A direct application of the moment method typically requires one to make a finite moment assumption such as
, but as we shall see, one can reduce fairly easily to this case by a truncation argument.
For the strong law of large numbers, one can also use methods relating to the theory of martingales, such as stopping time arguments and maximal inequalities; we present some classical arguments of Kolmogorov in this regard.
— 1. The moment method —
We begin by using the moment method to establish both the strong and weak law of large numbers for sums of iid random variables, under additional moment hypotheses.
We first make a very simple observation: in order to prove the weak or strong law of large numbers for complex variables, it suffices to do so for real variables, as the complex case follows from the real case after taking real and imaginary parts. Thus we shall restrict attention henceforth to real random variables, in order to avoid some unnecessarily complications involving complex conjugation.
Let be a sequence of iid copies of a scalar random variable
, and define the partial sums
. Suppose that
is absolutely integrable, with expectation (or mean)
. Then we can use linearity of expectation to compute the expectation (or first moment) of
:
In particular, the expectation of is
. This looks consistent with the strong and weak law of large numbers, but does not immediately imply these laws. However, thanks to Markov’s inequality, we do at least get the following very weak bound
for any , in the case that
is unsigned and absolutely integrable. Thus, in the unsigned case at least, we see that
usually doesn’t get much larger than the mean
. We will refer to (1) as a first moment bound on
, as it was obtained primarily through a computation of the first moment
of
.
Now we turn to second moment bounds on , obtained through computations of second moments such as
or
. It will be convenient to normalise the mean
to equal zero, by replacing each
with
(and
by
), so that
gets replaced by
(and
by
). With this normalisation, we see that to prove the strong or weak law of large numbers, it suffices to do so in the mean zero case
. (On the other hand, if
is unsigned, then normalising
in this fashion will almost certainly destroy the unsigned property, so it is not always desirable to perform this normalisation.)
Suppose that has finite second moment (i.e.
, that is to say
is square-integrable) and has been normalised to have mean zero. We write the variance
as
. The first moment calculation then shows that
has mean zero. Now we compute the variance of
, which in the mean zero case is simply
; note from the triangle inequality that this quantity is finite. By linearity of expectation, we have
(All expressions here are absolutely integrable thanks to the Cauchy-Schwarz inequality.) If , then the term
is equal to
. If
, then by hypothesis
and
are independent and mean zero, and thus
Putting all this together, we obtain
or equivalently
This bound was established in the mean zero case, but it is clear that it also holds in general, since subtracting a constant from a random variable does not affect its variance. Thus we see that while has the same mean
as
, it has a much smaller variance:
in place of
. This is the first demonstration of the concentration of measure effect that comes from combining many independent random variables
. (At the opposite extreme to the independent case, suppose we took
to all be exactly the same random variable:
. Then
has exactly the same mean and variance as
. Decorrelating the
does not affect the mean of
, but produces significant cancellations that reduce the variance.)
If we insert this variance bound into Chebyshev’s inequality, we obtain the bound
for any natural number and
, whenever
has mean
and a finite variance
. The right-hand side goes to zero as
for fixed
, so we have in fact established the weak law of large numbers in the case that
has finite variance.
Note that (2) implies that
converges to zero in probability whenever is a function of
that goes to infinity as
. Thus for instance
in probability. Informally, this means that tends to stray by not much more than
from
typically. This intuition will be reinforced in the next set of notes when we study the central limit theorem and related results such as the Chernoff inequality. (It is also supported by the law of the iterated logarithm, which we will probably not be able to get to in this set of notes.)
One can hope to use (2) and the Borel-Cantelli lemma (Exercise 2(ii)) to also obtain the strong law of large numbers in the second moment case, but unfortunately the quantities are not summable in
. To resolve this issue, we will go to higher moments than the second moment. One could calculate third moments such as
, but this turns out to not convey too much information (unless
is unsigned) because of the signed nature of
; the expression
would in principle convey more usable information, but is difficult to compute as
is not a polynomial combination of the
. Instead, we move on to the fourth moment. Again, we normalise
to have mean
, and now assume a finite fourth moment
(which, by the Hölder or Jensen inequalities, implies that all lower moments such as
are finite). We again use
to denote the variance of
. We can expand
Note that all expectations here are absolutely integrable by Hölder’s inequality and the hypothesis of finite fourth moment. The correlation looks complicated, but fortunately it simplifies greatly in most cases. Suppose for instance that
is distinct from
, then
is independent of
(even if some of the
are equal to each other) and so
since . Similarly for permutations. This leaves only a few quadruples
for which
could be non-zero: the three cases
,
,
where each of the indices
is paired up with exactly one other index; and the diagonal case
. If for instance
, then
Similarly for the cases and
, which gives a total contribution of
to
. Finally, when
, then
, and there are
contributions of this form to
. We conclude that
and hence by Markov’s inequality
for any . If we remove the normalisation
, we conclude that
The right-hand side decays like , which is now summable in
(in contrast to (2)). Thus we may now apply the Borel-Cantelli lemma and conclude the strong law of large numbers in the case when one has bounded fourth moment
.
One can of course continue to compute higher and higher moments of (assuming suitable finite moment hypotheses on
), though as one can already see from the fourth moment calculation, the computations become increasingly combinatorial in nature. We will pursue this analysis more in the next set of notes, when we discuss the central limit theorem. For now, we turn to some applications and variants of the moment method (many of which are taken from Durrett’s book).
We begin with two quick applications of the weak law of large numbers to topics outside of probability. We first give an explicit version of the Weierstrass approximation theorem, which asserts that continuous functions on (say) the unit interval can be approximated by polynomials.
Proposition 5 (Approximation by Bernstein polynomials) Let
be a continuous function. Then the Bernstein polynomials
converges uniformly to
as
.
Proof: We first establish the pointwise bound for each
. Fix
, and let
be iid Bernoulli variables (i.e. variables taking values in
) with each
equal to
with probability
. The mean of the
is clearly
, and the variance is bounded crudely by
(in fact it is
), so if we set
then by the weak law of large numbers for random variables of finite second moment, we see that
converges in probability to
(note that
is clearly dominated by
). By the dominated convergence theorem in probability, we conclude that
converges to
. But from direct computation we see that
takes values in
, with each
being attained with probability
(i.e.
as a binomial distribution), and so from the definition of the Bernstein polynomials
we see that
. This concludes the pointwise convergence claim.
To establish the uniform convergence, we use the proof of the weak law of large numbers, rather than the statement of that law, to get the desired uniformity in the parameter . For a given
, we see from (2) that
for any . On the other hand, as
is continuous on
, it is uniformly continuous, and so for any
there exists a
such that
whenever
with
. For such an
and
, we conclude that
On the other hand, being continuous on ,
must be bounded in magnitude by some bound
, so that
. This leads to the upper bound
and thus by the triangle inequality and the identity
Since is bounded by (say)
, and
can be made arbitrarily small, we conclude that
converges uniformly to
as required.
The other application of the weak law of large numbers is to the geometry of high-dimensional cubes, giving the rather unintuitive conclusion that most of the volume of the high-dimensional cube is contained in a thin annulus.
Proposition 6 Let
. Then, for sufficiently large
, a proportion of at least
of the cube
(by
-dimensional Lebesgue measure) is contained in the annulus
.
This proposition already indicates that high-dimensional geometry can behave in a manner quite differently from what one might naively expect from low-dimensional geometric intuition; one needs to develop a rather distinct high-dimensional geometric intuition before one can accurately make predictions in large dimensions.
Proof: Let be iid random variables drawn uniformly from
. Then the random vector
is uniformly distributed on the cube
. The variables
are also iid, and (by the change of variables formula) have mean
Hence, by the weak law of large numbers, the quantity converges in probability to
, so in particular the probability
goes to zero as goes to infinity. But this quantity is precisely the proportion of
that lies outside the annulus
, and the claim follows.
The first and second moment method are very general, and apply to sums of random variables
that do not need to be identically distributed, or even independent (although the bounds can get weaker and more complicated if one strays too far from these hypotheses). For instance, it is clear from linearity of expectation that
has mean
(assuming of course that are absolutely integrable) and variance
(assuming now that are square-integrable). (For the latter claim, it is convenient, as before, to first normalise each of the
to have mean zero.) If the
are pairwise independent in addition to being square-integrable, then all the covariances vanish, and we obtain additivity of the variance:
Remark 7 Viewing the variance as the square of the standard deviation, the identity (4) can be interpreted as a rigorous instantiation of the following informal principle of square root cancellation: if one has a sum
of random (or pseudorandom) variables that “oscillate” in the sense that their mean is either zero or close to zero, and each
has an expected magnitude of about
(in the sense that a statistic such as the standard deviation of
is comparable to
), and the
“behave independently”, then the sum
is expected to have a magnitude of about
. Thus for instance a sum of
unbiased signs
would be expected to have magnitude about
if the
do not exhibit strong correlations with each other. This principle turns out to be remarkably broadly applicable (at least as a heuristic, if not as a rigorous argument), even in situations for which no randomness is evident (e.g. in considering the type of exponential sums that occur in analytic number theory). We will see some further instantiations of this principle in later notes.
These identities, together with Chebyshev’s inequality, already gives some useful control on many statistics, including some which are not obviously of the form of a sum of independent random variables. A classic example of this is the coupon collector problem, which we formulate as follows. Let be a natural number, and let
be an infinite sequence of “coupons”, which are iid and uniformly distributed from the finite set
. Let
denote the first time at which one has collected all
different types of coupons, thus
is the first natural number for which the set
attains the maximal cardinality of
(or
if no such natural number exists, though it is easy to see that this is a null event, indeed note from the strong law of large numbers that almost surely one will collect infinitely many of each coupon over time). The question is then to describe the behaviour of
as
gets large.
At first glance, does not seem to be easily describable as the sum of many independent random variables. However, if one looks at it the right way, one can see such a structure emerge (and much of the art of probability is in finding useful and different ways of thinking of the same random variable). Namely, for each
, let
denote the first time one has collected
coupons out of
, thus
is the first non-negative integer such that
has cardinality
, with
If we then write for
, then the
take values in the natural numbers, we have the telescoping sum
Remarkably, the random variables have a simple structure:
Proposition 8 The random variables
are jointly independent, and each
has a geometric distribution with parameter
, in the sense that
for
and
.
The joint independence of the reflects the “Markovian” or “memoryless” nature of a certain process relating to the coupon collector problem, and can be easily established once one has understood the concept of conditional expectation, but the further exploration of these concepts will have to be deferred to the course after this one (which I will not be teaching or writing notes for). But as the coupon collecting problem is so simple, we shall proceed instead by direct computation.
Proof: It suffices to show that
for any choice of natural numbers . In order for the event
to hold, the first coupon
can be arbitrary (and
must be
), but the coupons
have to be equal to
; then
must be from one the remaining
elements of
not equal to
, and
must be from the two-element set
; and so on and so forth up to
. The claim then follows from a routine application of elementary combinatorics to count all the possible values for the tuple
of the above form and dividing by the total number
of such tuples.
Exercise 9 Show that if
is a geometric distribution with parameter
for some
(thus
for all
) then
has mean
and variance
.
From the above proposition and exercise as well as (3), (4) we see that
and
From the integral test (and crudely bounding ) one can thus obtain the bounds
and
where we use the usual asymptotic notation of denoting by any quantity bounded in magnitude by a constant multiple
of
. From Chebyshev’s inequality we thus see that
for any (note the bound is trivial unless
is large). This implies in particular that
converges to
in probability as
(assuming that our underlying probability space can model a separate coupon collector problem for each choice of
). Thus, roughly speaking, we see that one expects to take about
units of time to collect all
coupons.
Another application of the weak and strong law of large numbers (even with the moment hypotheses currently imposed on these laws) is a converse to the Borel-Cantelli lemma in the jointly independent case:
Exercise 10 (Second Borel-Cantelli lemma) Let
be a sequence of jointly independent events. If
, show that almost surely an infinite number of the
hold simultaneously. (Hint: compute the mean and variance of
. One can also compute the fourth moment if desired, but it is not necessary to do so for this result.)
One application of the second Borel-Cantelli lemma has the colourful name of the “infinite monkey theorem“:
Exercise 11 (Infinite monkey theorem) Let
be iid random variables drawn uniformly from a finite alphabet
. Show that almost surely, every finite word
of letters
in the alphabet appears infinitely often in the string
.
In the usual formulation of the weak or strong law of large numbers, we draw the sums from a single infinite sequence
of iid random variables. One can generalise the situation slightly by working instead with sums from rows of a triangular array, which are jointly independent within rows but not necessarily across rows:
Exercise 12 (Triangular arrays) Let
be a triangular array of scalar random variables
, such that for each
, the row
is a collection of independent random variables. For each
, we form the partial sums
.
- (i) (Weak law) If all the
have mean
and
, show that
converges in probability to
.
- (ii) (Strong law) If all the
have mean
and
, show that
converges almost surely to
.
Note that the weak and strong law of large numbers established previously corresponds to the case when the triangular array collapses to a single sequence
of iid random variables.
We now illustrate the use of moment method and law of large number methods to two important examples of random structures, namely random graphs and random matrices.
Exercise 13 For a natural number
and a parameter
, define an Erdös-Renyi graph on
vertices with parameter
to be a random graph
on a (deterministic) vertex set
of
vertices (thus
is a random variable taking values in the discrete space of all
possible graphs one can place on
) such that the events
for unordered pairs
in
are jointly independent and each occur with probability
.
For each, let
be an Erdös-Renyi graph on
vertices with parameter
(we do not require the graphs to be independent of each other).
- (i) If
is the number of edges in
, show that
converges almost surely to
. (Hint: use Exercise 12.)
- (ii) If
is the number of triangles in
(i.e. the set of unordered triples
in
such that
), show that
converges in probability to
. (Note: there is not quite enough joint independence here to directly apply the law of large numbers, however the second moment method still works nicely.)
- (iii) Show in fact that
converges almost surely to
. (Note: in contrast with the situation with the strong law of large numbers, the fourth moment does not need to be computed here.)
Exercise 14 For each
, let
be a random
matrix (i.e. a random variable taking values in the space
or
of
matrices) such that the entries
of
are jointly independent in
and take values in
with a probability of
each. (Such matrices are known as random sign matrices.) We do not assume any independence for the sequence
.
- (i) Show that the random variables
are deterministically equal to
, where
denotes the adjoint (which, in this case, is also the transpose) of
and
denotes the trace (sum of the diagonal entries) of a matrix.
- (ii) Show that for any natural number
, the quantities
are bounded uniformly in
(i.e. they are bounded by a quantity
that can depend on
but not on
). (You may wish to first work with simple cases like
or
to gain intuition.)
- (iii) If
denotes the operator norm of
, and
, show that
converges almost surely to zero, and that
diverges almost surely to infinity. (Hint: use the spectral theorem to relate
with the quantities
.)
One can obtain much sharper information on quantities such as the operator norm of a random matrix; see this previous blog post for further discussion.
Exercise 15 The Cramér random model for the primes is a random subset
of the natural numbers with
,
, and the events
for
being jointly independent with
(the restriction to
is to ensure that
is less than
). It is a simple, yet reasonably convincing, probabilistic model for the primes
, which can be used to provide heuristic confirmations for many conjectures in analytic number theory. (It can be refined to give what are believed to be more accurate predictions; see this previous blog post for further discussion.)
- (i) (Probabilistic prime number theorem) Prove that almost surely, the quantity
converges to one as
.
- (ii) (Probabilistic Riemann hypothesis) Show that if
, then the quantity
converges almost surely to zero as
.
- (iii) (Probabilistic twin prime conjecture) Show that almost surely, there are an infinite number of elements
of
such that
also lies in
.
- (iv) (Probabilistic Goldbach conjecture) Show that almost surely, all but finitely many natural numbers
are expressible as the sum of two elements of
.
Probabilistic methods are not only useful for getting heuristic predictions about the primes; they can also give rigorous results about the primes. We give one basic example, namely a probabilistic proof (due to Turán) of a theorem of Hardy and Ramanujan, which roughly speaking asserts that a typical large number has about
distinct prime factors.
Exercise 16 (Hardy-Ramanujan theorem) Let
be a natural number (so in particular
), and let
be a natural number drawn uniformly at random from
to
. Assume Mertens’ theorem
for all
, where the sum is over primes up to
.
- (i) Show that the random variable
(where
is
when
divides
and
otherwise, and the sum is over primes up to
) has mean
and variance
. (Hint: compute (up to reasonable error) the means, variances and covariances of the random variables
.)
- (ii) If
denotes the number of distinct prime factors of
, show that
converges to
in probability as
. (Hint: first show that
.) More precisely, show that
converges in probability to zero, whenever
is any function such that
goes to infinity as
.
Exercise 17 (Shannon entropy) Let
be a finite non-empty set of some cardinality
, and let
be a random variable taking values in
. Define the Shannon entropy
to be the quantity
with the convention that
. (In some texts, the logarithm to base
is used instead of the natural logarithm
.)
- (i) Show that
. (Hint: use Jensen’s inequality.) Determine when the equality
holds.
- (ii) Let
and
be a natural number. Let
be
iid copies of
, thus
is a random variable taking values in
, and the distribution
is a probability measure on
. Let
denote the set
Show that if
is sufficiently large, then
and
(Hint: use the weak law of large numbers to understand the number of times each element
of
occurs in
.)
Thus, roughly speaking, while
in principle takes values in all of
, in practice it is concentrated in a set of size about
, and is roughly uniformly distributed on that set. This is the beginning of the microstate interpretation of Shannon entropy, but we will not develop the theory of Shannon entropy further in this course.
— 2. Truncation —
The weak and strong laws of large numbers have been proven under additional moment assumptions (of finite second moment and finite fourth moment respectively). To remove these assumptions, we use the simple but effective truncation method, decomposing a general scalar random variable into a truncated component such as
for some suitable threshold
, and a tail
. The main term
is bounded and thus has all moments finite. The tail
will not have much better moment properties than the original variable
, but one can still hope to make it “small” in various ways. There is a tradeoff regarding the selection of the truncation parameter
: if
is too large, then the truncated component
has poor estimates, but if
is too small then the tail
causes trouble.
Let’s first see how this works with the weak law of large numbers. As before, we assume we have an iid sequence copies of a real absolutely integrable
with no additional finite moment hypotheses. We write
. At present, we cannot take variances of the
or
and so the second moment method is not directly available. But we now perform a truncation; it turns out that a good choice of threshold here is
, thus we write
where
and
, and then similarly decompose
where
and
as for any given
(not depending on
). By the triangle inequality, we can split
We begin by studying .
The random variables are iid with mean
and variance at most
Thus, has mean
and variance at most
. By dominated convergence,
as
, so for sufficiently large
we can bound
and hence by the Chebyshev inequality
Observe that is bounded surely by the absolutely integrable
, and goes to zero as
, so by dominated convergence we conclude that
as (keeping
fixed).
To handle , we observe that each
is only non-zero with probability
, and hence by subadditivity
By dominated convergence again, as
, and thus
Putting all this together, we conclude (5) as required. This concludes the proof of the weak law of large numbers (in the iid case) for arbitrary absolutely integrable . For future reference, we observe that the above arguments give the bound
whenever is sufficiently large depending on
.
Due to the reliance on the dominated convergence theorem, the above argument does not provide any uniform rate of decay in (5). Indeed there is no such uniform rate. Consider for instance the sum where
are iid random variables that equal
with probability
and
with probability
. Then the
are unsigned and all have mean
, but
vanishes with probability
, which converges to
as
. Thus we see that the probability that
stays a distance
from the mean value of
is bounded away from zero. This is not inconsistent with the weak law of large numbers, because the underlying random variable
depends on
in this example. However, it rules out an estimate of the form
that holds uniformly whenever obeys the bound
, and
is a quantity that goes to zero as
for a fixed choice of
. (Contrast this with (2), which does provide such a uniform bound if one also assumes a bound on the second moment
.)
One can ask what happens to the when the underlying random variable
is not absolutely integrable. In the unsigned case, we have
Exercise 18 Let
be iid copies of an unsigned random variable
with infinite mean, and write
. Show that
diverges to infinity in probability, in the sense that
as
for any fixed
.
The above exercise shows that grows faster than
(in probability, at least) when
is unsigned with infinite mean, but this does not completely settle the question of the precise rate at which
does grow. We will not answer this question in full generality here, but content ourselves with analysing a classic example of the unsigned infinite mean setting, namely the Saint Petersburg paradox. The paradox can be formulated as follows. Suppose we have a lottery whose payout
takes taking values in the powers of two
with
for . The question is to work out what is the “fair” or “breakeven” price to pay for a lottery ticket. If one plays this lottery
times, the total payout is
where
are independent copies of
, so the question boils down to asking what one expects the value of
to be. If
were absolutely integrable, the strong or weak law of large numbers would indicate that
is the fair price to pay, but in this case we have
This suggests, paradoxically, that any finite price for this lottery, no matter how high, would be a bargain!
To clarify this paradox, we need to get a better understanding of the random variable . For a given
, we let
be a truncation parameter to be chosen later, and split
where
and
as before (we no longer need the absolute value signs here as all random variables are unsigned). Since the
take values in powers of two, we may as well also set
to be a power of two. We split
where
and
The random variable can be computed to have mean
and we can upper bound the variance by
and hence has mean
and variance at most
. By Chebyshev’s inequality, we thus have
for any .
Now we turn to . We cannot use the first or second moment methods here because the
are not absolutely integrable. However, we can instead use the following “zeroth moment method” argument. Observe that the random variable
is only nonzero with probability
(that is to say, the “zeroth moment”
is
, using the convention
). Thus
is nonzero with probability at most
. We conclude that
This bound is valid for any natural number and any
. Of course for this bound to be useful, we want to select parameters so that the right-hand side is somewhat small. If we pick for instance
to be the integer part of
, and
to be
, we see that
which (for large ) implies that
In particular, we see that converges in probability to one. This suggests that the fair price to pay for the Saint Petersburg lottery is a function of the number
of tickets one wishes to play, and should be approximately
when
is large. In particular, the lottery is indeed worth paying out any finite cost
, but one needs to buy about
tickets before one breaks even!
In contrast to the absolutely integrable case, in which the weak law can be upgraded to the strong law, there is no strong law for the Saint Petersburg paradox:
Exercise 19 With the notation as in the above analysis of the Saint Petersburg paradox, show that
is almost surely unbounded. (Hint: it suffices to show that
is almost surely unbounded. For this, use the second Borel-Cantelli lemma.)
The following exercise can be viewed as a continuous analogue of the Saint Petersburg paradox.
Exercise 20 A real random variable
is said to have a standard Cauchy distribution if it has the probability density function
.
- (i) Verify that standard Cauchy distributions exist (this boils down to checking that the integral of the probability density function is
).
- (ii) Show that a real random variable with the standard Cauchy distribution is not absolutely integrable.
- (iii) If
are iid copies of a random variable
with the standard Cauchy distribution, show that
converges in probability to
but is almost surely unbounded.
Exercise 21 (Weak law of large numbers for triangular arrays) Let
be a triangular array of random variables, with the variables
jointly independent for each
. Let
be a sequence going to infinity, and write
and
. Assume that
and
as
. Show that
in probability.
Now we turn to establishing the strong law of large numbers in full generality. A first attempt would be to apply the Borel-Cantelli lemma to the bound (6). However, the decay rates for quantities such as are far too weak to be absolutely summable, in large part due to the reliance on the dominated convergence theorem. To get around this we follow some arguments of Etemadi. We first need to make a few preliminary reductions, aimed at “sparsifying” the set of times
that one needs to control. It is here that we will genuinely use the fact that the averages
are being drawn from a single sequence
of random variables, rather than from a triangular array.
We turn to the details. In previous arguments it was convenient to normalise the underlying random variable to have mean zero. Here we will use a different reduction, namely to the case when
is unsigned; the strong law for real absolutely integrable
clearly follows from the unsigned case by expressing
as the difference of two unsigned absolutely integrable variables
and
(and splitting
similarly).
Henceforth we assume (and hence the
) to be unsigned. Crucially, this now implies that the partial sums
are monotone:
. While this does not quite imply any monotonicity on the sequence
, it does make it significantly easier to show that it converges. The key point is as follows.
Lemma 22 Let
be an increasing sequence, and let
be a real number. Suppose that for any
, the sequence
converges to
as
, where
. Then
converges to
.
Proof: Let . For any
, let
be the index such that
. Then we have
and (for sufficiently large )
and thus
Taking limit inferior and superior, we conclude that
and then sending we obtain the claim.
An inspection of the above argument shows that we only need to verify the hypothesis for a countable sequence of (e.g.
for natural number
). Thus, to show that
converges to
almost surely, it suffices to show that for any
, one has
almost surely as
.
Fix . The point is that the “lacunary” sequence
is much sparser than the sequence of natural numbers
, and one now will lose a lot less from the Borel-Cantelli argument. Indeed, for any
, we can apply (6) to conclude that
whenever is sufficiently large depending on
. Thus, by the Borel-Cantelli lemma, it will suffice to show that the sums
and
are finite. Using the monotone convergence theorem to interchange the sum and expectation, it thus suffices to show the pointwise estimates
and
for some . But this follows from the geometric series formula (the first sum is over the elements of the sequence
that are greater than or equal to
, while the latter is over those that are less than
). This proves the strong law of large numbers for arbitrary absolutely integrable iid
.
We remark that by carefully inspecting the above proof of the strong law of large numbers, we see that the hypothesis of joint independence of the can be relaxed to pairwise independence.
The next exercise shows how one can use the strong law of large numbers to approximate the cumulative distribution function of a random variable by an empirical cumulative distribution function.
Exercise 23 Let
be iid copies of a real random variable
.
- (i) Show that for every real number
, one has almost surely that
and
as
.
- (ii) Establish the Glivenko-Cantelli theorem: almost surely, one has
uniformly in
as
. (Hint: For any natural number
, let
denote the largest integer multiple of
less than
. Show first that
is within
of
for all
when
is sufficiently large.)
Exercise 24 (Lack of strong law for triangular arrays) Let
be a random variable taking values in the natural numbers with
, where
(this is an example of a zeta distribution).
- (i) Show that
is absolutely integrable.
- (ii) Let
be jointly independent copies of
. Show that the random variables
are almost surely unbounded. (Hint: for any constant
, show that
occurs with probability at least
for some
depending on
. Then use the second Borel-Cantelli lemma.)
— 3. The Kolmogorov maximal inequality —
Let be a sequence of jointly independent square-integrable real random variables of mean zero; we do not assume the
to be identically distributed. As usual, we form the sums
, then
has mean zero and variance
From Chebyshev’s inequality, we thus have
for any and natural number
. Perhaps surprisingly, we have the following improvement to this bound, known as the Kolmogorov maximal inequality:
Theorem 25 (Kolmogorov maximal inequality) With the notation and hypotheses as above, we have
Proof: For each , let
be the event that
, but that
for all
. It is clear that the event
is the disjunction of the disjoint events
, thus
On the event , we have
, and hence
We will shortly prove the inequality
for all . Assuming this inequality for the moment, we can put together all the above estimates, using the disjointness of the
, to conclude that
and the claim follows from (7).
It remains to prove (8). Since
we have
But note that the random variable is completely determined by
, while
is completely determined by the
. Thus
and
are independent. Since
also has mean zero, we have
and the claim (8) follows.
An inspection of the above proof reveals that the key ingredient is the lack of correlation between past and future – a variable such as , which is determined by the portion of the sequence
to the “past” (and present) of
, is uncorrelated with a variable such as
that depends only on the “future” of
. One can formalise such a lack of correlation through the concept of a martingale, which will be covered in later courses in this sequence but which is beyond the scope of these notes. The use of the first time
at which
exceeds or attains the threshold
is a simple example of a stopping time, which will be a heavily used concept in the theory of martingales (and is also used extensively in harmonic analysis, which is also greatly interested in establishing maximal inequalities).
The Kolmogorov maximal inequality gives the following variant of the strong law of large numbers.
Theorem 26 (Convergence of random series) Let
be jointly independent square-integrable real random variables of mean zero with
Then the series
is almost surely convergent (i.e., the partial sums converge almost surely).
Proof: From the Kolmogorov maximal inequality and continuity from below we have
This is already enough to show that the partial sums are almost surely bounded in
, but this isn’t quite enough to establish conditional convergence. To finish the job, we apply (9) with
replaced by the shifted sequence
for a natural number
to conclude that
Sending to infinity using continuity from above, we conclude that
for all ; applying this for all rational
, we conclude that
is almost surely a Cauchy sequence, and the claim follows.
We can use this result together with some elementary manipulation of sums to give the following alternative proof of the strong law of large numbers.
Theorem 27 (Strong law of large numbers) Let
be iid copies of an absolutely integrable variable
of mean
, and let
. Then
converges almost surely to
.
Proof: We may normalise to be real valued with
. Note that that
and hence by the Borel-Cantelli lemma we almost surely have for all but finitely many
. Thus if we write
and
, then the difference between
and
almost surely goes to zero as
. Thus it will suffice to show that
goes to zero almost surely.
The random variables are still jointly independent, but are not quite mean zero. However, the normalised random variables
are of mean zero and
so by Theorem 26 we see that the sum is almost surely convergent.
Write , thus the sequence
is almost surely a Cauchy sequence. From the identity
we conclude that the sequence almost surely converges to zero, that is to say
almost surely. On the other hand, we have
and hence by dominated convergence
as , which implies that
as . By the triangle inequality, we conclude that
almost surely, as required.
Exercise 28 (Kronecker lemma) Let
be a convergent series of real numbers
, and let
be a sequence tending to infinity. Show that
converges to zero as
. (This is known as Kronecker’s lemma; the special case
was implicitly used in the above argument.)
Exercise 29 (Kolmogorov three-series theorem, one direction) Let
be a sequence of jointly independent real random variables, and let
. Suppose that the two series
and
are absolutely convergent, and the third series
is convergent. Show that the series
is almost surely convergent. (The converse claim is also true, and will be discussed in later notes; the two claims are known collectively as the Kolmogorov three-series theorem.)
One advantage that the maximal inequality approach to the strong law of large numbers has over the moment method approach is that it tends to offer superior bounds on the (almost sure) rate of convergence. We content ourselves with just one example of this:
Exercise 30 (Cheap law of iterated logarithm) Let
be a sequence of jointly independent real random variables of mean zero and bounded variance (thus
). Write
. Show that
converges almost surely to zero as
for any given
. (Hint: use Theorem 26 and the Kronecker lemma for a suitable weighted sum of the
.) There is a more precise version of this fact known as the law of the iterated logarithm, which is beyond the scope of these notes.
The exercises below will be moved to a more appropriate location later, but are currently placed here in order to not disrupt existing numbering.
Exercise 31 Let
be iid copies of an absolutely integrable random variable
with mean
. Show that the averages
converge in
to
, that is to say that
as
.
Exercise 32 A scalar random variable
is said to be in weak
if one has
Thus Markov’s inequality tells us that every absolutely integrable random variable is in weak
, but the converse is not true (e.g. random variables with the Cauchy distribution are weak
but not absolutely integrable). Show that if
are iid copies of an unsigned weak
random variable, then there exists quantities
such that
converges in probability to
, where
. (Thus: there is a weak law of large numbers for weak
random variables, and a strong law for strong
(i.e. absolutely integrable) random variables.)
Exercise 33 Let
be iid copies of a real symmetric random variable
(thus
has the same distribution as
), and write
for
. For any
, show that
(Hint: for each
, show that
is non-negative with probability at least
. Then use the stopping time argument used to prove the Kolmogorov maximal inequality.)
Exercise 34 (Lévy’s inequality) Let
be i.i.d. copies of a real random variable
, and write
for
. Suppose one has
with the property that
for
. Show that
(Hint: for each
, show that
is at least
with probability at least
. Then use the stopping time argument used to prove the Kolmogorov maximal inequality.)

97 comments
Comments feed for this article
15 April, 2024 at 4:54 pm
Anonymous
Dear professor Tao: For part (i) Exercise 15, as are summable, by your previous comment and the Borel-Cantelli lemma it follows that
are summable, by your previous comment and the Borel-Cantelli lemma it follows that 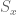 converges to
converges to  almost surely. Is this correct?
almost surely. Is this correct?
16 April, 2024 at 7:42 am
Anonymous
Wait, the root test gives 1 and one can’t conclude summability in this case. May I ask how is it that Chebyshev’s inequality is sufficient here?
23 April, 2024 at 6:39 pm
Anonymous
Dear prof Tao:
For part (i) of Exercise 15, if we let let , do you recommend calculating the fourth moment
, do you recommend calculating the fourth moment  for the Borel-Cantelli lemma? Do we need to use the triangular arrays form as in Exercise 12?
for the Borel-Cantelli lemma? Do we need to use the triangular arrays form as in Exercise 12?
25 April, 2024 at 3:56 pm
Anonymous
Dear prof Tao:
May I ask if the solution to part (2) of Exercise 15 requires the use of part (1)?
[It is a stronger statement, and is more difficult to prove. Strictly speaking one could attack (2) directly without first establishing (1), but for beginners I would recommend trying (1) first. -T.]
29 April, 2024 at 10:59 pm
Anonymous
Dear professor Tao:
In part (2) of Exercise 15, let be independent Bernoulli random variables of parameter
be independent Bernoulli random variables of parameter  . if one considers the partial sums
. if one considers the partial sums 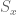 of
of  from
from  up to
up to  , where
, where  equals
equals  over
over  , then the moment method for the fourth moment stills seems not strong enough for one to show that
, then the moment method for the fourth moment stills seems not strong enough for one to show that 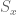 converges almost surely to zero. May I ask if this is the correct approach to pursuit, or if one needs to go to even higher moment?
converges almost surely to zero. May I ask if this is the correct approach to pursuit, or if one needs to go to even higher moment?
10 May, 2024 at 8:19 pm
Terence Tao
For this problem, one needs to work with a high moment that depends on (or else utilize a more powerful concentration inequality, such as Hoeffding’s inequality).
(or else utilize a more powerful concentration inequality, such as Hoeffding’s inequality).
7 May, 2024 at 11:35 am
Anonymous
Dear professor Tao:
Since part (3) of Exercise 15 only asks for a qualitative prediction on the number of twin Cramer random model primes, is it possible to work out a solution without obtaining a bound as explicit as the one obtained in Prediction 8 of your note for 254A, Supplement 4?
10 May, 2024 at 8:46 pm
Terence Tao
Yes, there are multiple ways to approach this question, that give various levels of strength in their conclusion. For instance, one relatively easy way to proceed here is to locate a number of independent events that would produce twins, and apply the converse of the Borel-Cantelli lemma for independent events.