I recently reposted my favourite logic puzzle, namely the blue-eyed islander puzzle. I am fond of this puzzle because in order to properly understand the correct solution (and to properly understand why the alternative solution is incorrect), one has to think very clearly (but unintuitively) about the nature of knowledge.
There is however an additional subtlety to the puzzle that was pointed out in comments, in that the correct solution to the puzzle has two components, a (necessary) upper bound and a (possible) lower bound (I’ll explain this further below the fold, in order to avoid blatantly spoiling the puzzle here). Only the upper bound is correctly explained in the puzzle (and even then, there are some slight inaccuracies, as will be discussed below). The lower bound, however, is substantially more difficult to establish, in part because the bound is merely possible and not necessary. Ultimately, this is because to demonstrate the upper bound, one merely has to show that a certain statement is logically deducible from an islander’s state of knowledge, which can be done by presenting an appropriate chain of logical deductions. But to demonstrate the lower bound, one needs to show that certain statements are not logically deducible from an islander’s state of knowledge, which is much harder, as one has to rule out all possible chains of deductive reasoning from arriving at this particular conclusion. In fact, to rigorously establish such impossiblity statements, one ends up having to leave the “syntactic” side of logic (deductive reasoning), and move instead to the dual “semantic” side of logic (creation of models). As we shall see, semantics requires substantially more mathematical setup than syntax, and the demonstration of the lower bound will therefore be much lengthier than that of the upper bound.
To complicate things further, the particular logic that is used in the blue-eyed islander puzzle is not the same as the logics that are commonly used in mathematics, namely propositional logic and first-order logic. Because the logical reasoning here depends so crucially on the concept of knowledge, one must work instead with an epistemic logic (or more precisely, an epistemic modal logic) which can properly work with, and model, the knowledge of various agents. To add even more complication, the role of time is also important (an islander may not know a certain fact on one day, but learn it on the next day), so one also needs to incorporate the language of temporal logic in order to fully model the situation. This makes both the syntax and semantics of the logic quite intricate; to see this, one only needs to contemplate the task of programming a computer with enough epistemic and temporal deductive reasoning powers that it would be able to solve the islander puzzle (or even a smaller version thereof, say with just three or four islanders) without being deliberately “fed” the solution. (The fact, therefore, that humans can grasp the correct solution without any formal logical training is therefore quite remarkable.)
As difficult as the syntax of temporal epistemic modal logic is, though, the semantics is more intricate still. For instance, it turns out that in order to completely model the epistemic state of a finite number of agents (such as 1000 islanders), one requires an infinite model, due to the existence of arbitrarily long nested chains of knowledge (e.g. “ knows that
knows that
knows that
has blue eyes”), which cannot be automatically reduced to shorter chains of knowledge. Furthermore, because each agent has only an incomplete knowledge of the world, one must take into account multiple hypothetical worlds, which differ from the real world but which are considered to be possible worlds by one or more agents, thus introducing modality into the logic. More subtly, one must also consider worlds which each agent knows to be impossible, but are not commonly known to be impossible, so that (for instance) one agent is willing to admit the possibility that another agent considers that world to be possible; it is the consideration of such worlds which is crucial to the resolution of the blue-eyed islander puzzle. And this is even before one adds the temporal aspect (e.g. “On Tuesday,
knows that on Monday,
knew that by Wednesday,
will know that
has blue eyes”).
Despite all this fearsome complexity, it is still possible to set up both the syntax and semantics of temporal epistemic modal logic in such a way that one can formulate the blue-eyed islander problem rigorously, and in such a way that one has both an upper and a lower bound in the solution. The purpose of this post is to construct such a setup and to explain the lower bound in particular. The same logic is also useful for analysing another well-known paradox, the unexpected hanging paradox, and I will do so at the end of the post. Note though that there is more than one way to set up epistemic logics, and they are not all equivalent to each other.
(On the other hand, for puzzles such as the islander puzzle in which there are only a finite number of atomic propositions and no free variables, one at least can avoid the need to admit predicate logic, in which one has to discuss quantifiers such as and
. A fully formed predicate temporal epistemic modal logic would indeed be of terrifying complexity.)
Our approach here will be a little different from the approach commonly found in the epistemic logic literature, in which one jumps straight to “arbitrary-order epistemic logic” in which arbitrarily long nested chains of knowledge (“ knows that
knows that
knows that \ldots”) are allowed. Instead, we will adopt a hierarchical approach, recursively defining for
a “
-order epistemic logic” in which knowledge chains of depth up to
, but no greater, are permitted. The arbitrarily order epistemic logic is then obtained as a limit (a direct limit on the syntactic side, and an inverse limit on the semantic side, which is dual to the syntactic side) of the finite order epistemic logics.
I should warn that this is going to be a rather formal and mathematical post. Readers who simply want to know the answer to the islander puzzle would probably be better off reading the discussion at the puzzle’s own blog post instead.
— 1. Zeroth-order logic —
Before we plunge into the full complexity of epistemic logic (or temporal epistemic logic), let us first discuss formal logic in general, and then focus on a particularly simple example of a logic, namely zeroth order logic (better known as propositional logic). This logic will end up forming the foundation for a hierarchy of epistemic logics, which will be needed to model such logic puzzles as the blue-eyed islander puzzle.
Informally, a logic consists of three inter-related components:
- A language. This describes the type of sentences the logic is able to discuss.
- A syntax. This describes the rules by which the logic can deduce conclusions (from given hypotheses).
- A semantics. This describes the sentences which the logic interprets to be true (in given models).
A little more formally:
- A language is a set
of sentences, which are certain strings of symbols from a fixed alphabet, that are generated by some rules of grammar.
- A syntax is a collection of inference rules for generating deductions of the form
(which we read as “From
, we can deduce
” or “
is a consequence of
“), where
and
are sentences in
(or sets of sentences in
).
- A semantics describes what a model (or interpretation, or structure, or world)
of the logic is, and defines what it means for a sentence
in
(or a collection of sentences) to be true in such a model
(which we write as
, and we read as “
models
“, “
obeys
“, or “
is true in
“).
We will abuse notation a little bit and use the language as a metonym for the entire logic; strictly speaking, the logic should be a tuple
consisting of the language, syntax, and semantics, but this leads to very unwieldy notation.
The syntax and semantics are dual to each other in many ways; for instance, the syntax can be used to show that certain statements can be proved, while the semantics can be used to show that certain statements cannot be proved. This distinction will be particularly important in the blue-eyed islander puzzle; in order to show that all blue-eyed islanders commit suicide by the 100th day, one can argue purely on syntactical grounds; but to show that it is possible for the blue-eyed islanders to not commit suicide on the 99th day or any preceding day, one must instead use semantic methods.
To illustrate the interplay between language, syntax, and semantics, we begin with the simple example of propositional logic. To describe this logic, one must first begin with some collection of atomic propositions. For instance, on an island with three islanders , one could consider the propositional logic generated by three atomic propositions
, where each
is intended to model the statement that
has blue eyes.
One can have either a finite or an infinite set of atomic propositions. In this discussion, it will suffice to consider the situation in which there are only finitely many atomic propositions, but one can certainly also study logics with infinitely many such propositions.
The language would then consist of all the sentences that can be formed from the atomic propositions using the usual logical connectives (
,
,
,
,
,
, etc.) and parentheses, according to the usual rules of logical grammar (which consists of rules such as “If
and
are sentences in
, then
is also a sentence in
“). For instance, if
are atomic propositions, then
would be an example of a sentence in . On the other hand,
is not a sentence in , despite being a juxtaposition of atomic propositions, connectives, and parentheses, because it is not built up from rules of grammar.
One could certainly write down a finite list of all the rules of grammar for propositional calculus (as is done for instance at this Wikipedia page), but we will not do so here in order not to disrupt the flow of discussion.
It is customary to abuse notation slightly and omit parentheses when they are redundant (or when there is enough associativity present that the precise placement of parentheses are not relevant). For instance, could be abbreviated as
. We will adopt this type of convention in order to keep the exposition as uncluttered as possible.
Now we turn to the syntax of propositional logic. This syntax is generated by basic rules of deductive logic, such as modus ponens
or the law of the excluded middle
and completed by transitivity (if and
, then
), monotonicity (
), and concatenation (if
and
then
). (Here we adopt the usual convention of representing a set of sentences without using the usual curly braces, instead relying purely on the comma separator.) Another convenient inference rule to place in this logic is the deduction theorem: if
, then one can infer
. (In propositional logic (or predicate logic), this rule is redundant (hence the designation of this rule as a theorem), but for the epistemic logics below, it will be convenient to make deduction an explicit inference rule, as it simplifies the other inference rules one will have to add to the system.)
A typical deduction that comes from this syntax is
which using the blue-eyed islander interpretation, is the formalisation of the assertion that given that at least one of the islanders has blue eyes, and that
do not have blue eyes, one can deduce that
has blue eyes.
As with the laws of grammar, one can certainly write down a finite list of inference rules in propositional calculus; one such list for instance is given at this Wikipedia page. Note though that, much as a given vector space has more than one set of generators, there is more than one possible list of inference rules for propositional calculus, due to some rules being equivalent to, or at least deducible from, other rules; the precise choice of basic inference rules is to some extent a matter of personal taste and will not be terribly relevant for the current discussion.
Finally, we discuss the semantics of propositional logic. For this particular logic, the models are described by truth assignments, that assign a truth value
to each atomic statement
. Once a truth value
to each atomic statement
is assigned, the truth value
of any other sentence
in the propositional logic generated by these atomic statements can then be interpreted using the usual truth tables. For instance, returning to the islander example, consider a model
in which
is true, but
and
are false; informally,
describes a hypothetical world in which
has blue eyes but
and
do not have blue eyes. Then the sentence
is true in
,
but the statement is false in
,
If is a set of sentences, we say that
models
if
models each sentence in
. Thus for instance, if we continue the preceding example, then
but
Note that if there are only finitely many atomic statements , then there are only finitely many distinct models
of the resulting propositional logic; in fact, there are exactly
such models, one for each truth assignment. We will denote the space of all possible models of a language
as
.
If one likes, one can designate one of these models to be the “real” world so that all the other models become purely hypothetical worlds. In the setting of propositional logic, the hypothetical worlds then have no direct bearing on the real world; the fact that a sentence
is true or false in a hypothetical world
does not say anything about what sentences are true or false in
. However, when we turn to epistemic logics later in this post, we will see that hypothetical worlds will play an important role in the real world, because such worlds may be considered to be possible worlds by one or more agents (or, an agent may consider it possible that another agent considers the world to be possible, and so forth.).
The syntatical and semantic sides of propositional logic are tied together by two fundamental facts:
Theorem 1 (Soundness and completeness) Let
be a propositional logic, and let
be a set of sentences in
, and let
be another sentence in
.
- (Soundness) If
, then every model
which obeys
, also obeys
(i.e.
implies
).
- (Completeness) If every model
that obeys
, also obeys
, then
.
Soundness is easy to prove; one merely needs to verify that each of the inference rules in one’s syntax is valid, in that models that obey
, automatically obey
. This boils down to some tedious inspection of truth tables. (The soundness of the deduction theorem is a little trickier to prove, but one can achieve this by an induction on the number of times this theorem is invoked in a given induction.) Completeness is a bit more difficult to establish; this claim is in fact a special case of the Gödel completeness theorem, and is discussed in this previous blog post; we also sketch a proof of completeness below.
By taking the contrapositive of soundness, we have the following important corollary: if we can find a model which obeys
but does not obey
, then it must not be possible to deduce
as a logical consequence of
:
. Thus, we can use semantics to demonstrate limitations in syntax.
For instance, consider a truth assignment in which
is true but
is false. Then
, but
. This demonstrates that
thus an implication such as does not entail its converse
.
A theory (or more precisely, a deductive theory) in a logic , is a set of sentences
in
which is closed under deductive consequence, thus if
for some sentence
in
, then
. Given a theory
, one can associate the set
of all possible worlds (or models) in which that theory is true; conversely, given a set of such models, one can form the theory
of sentences which are true in all models in . If the logic
is both sound and complete, these operations invert each other: given any theory
, we have
, and given any set
of models,
is a theory and
. Thus there is a one-to-one correspondence between theories and sets of possible worlds in a sound complete language
.
For instance, in our running example, if is the theory generated by the three statements
,
, and
, then
consists of precisely two worlds; one in which
are true and
is false, and one in which
is true and
are false. Since neither of
or
are true in both worlds in
, neither of
or
lie in
. Thus, it is not possible to deduce either of
or
from the hypotheses
,
, and
. More informally, if one knows that there is at least one blue-eyed islander, that
has blue eyes, and
does not have blue eyes, this is not enough information to determine whether
has blue eyes or not.
One can use theories to prove the completeness theorem. Roughly speaking, one can argue by taking the contrapositive. Suppose that , then we can find a theory which contains all sentences in
, but does not contain
. In this finite setting, we can easily pass to a maximal such theory (with respect to set inclusion); one then easily verifies that this theory is complete in the sense that for any given sentence
, exactly one of
and
is true. From this complete theory one can then directly build a model
which obeys
but does not obey
, giving the desired claim.
— 2. First-order epistemic logic —
Having reviewed propositional logic (which we will view as the zeroth-order iteration of epistemic logic), we now turn to the first non-trivial example of epistemic logic, which we shall call first-order epistemic logic (which should not be confused with the more familiar first-order predicate logic). Roughly speaking, first-order epistemic logic is like zeroth-order logic, except that there are now also some knowledge agents that are able to know certain facts in zeroth-order logic (e.g. an islander may know that the islander
has blue eyes). However, in this logic one cannot yet express higher-order facts (e.g. we will not yet be able to formulate a sentence to the effect that
knows that
knows that
has blue eyes). This will require a second-order or higher epistemic logic, which we will discuss later in this post.
Let us now formally construct this logic. As with zeroth-order logic, we will need a certain set of atomic propositions, which for simplicity we will assume to be a finite set . This already gives the zeroth order language
of sentences that one can form from the
by the rules of propositional grammar. For instance,
is a sentence in . The zeroth-order logic
also comes with a notion of inference
and a notion of modeling
, which we now subscript by
in order to distinguish it from the first-order notions of inference
and modeling
which we will define shortly. Thus, for instance
and if is a truth assignment for
for which
are all true, then
We will also assume the existence of a finite number of knowledge agents , each of which are capable of knowing sentences in the zeroth order language
. (In the case of the islander puzzle, and ignoring for now the time aspect of the puzzle, each islander
generates one knowledge agent
, representing the state of knowledge of
at a fixed point in time. Later on, when we add in the temporal aspect to the puzzle, we will need different knowledge agents for a single islander at different points in time, but let us ignore this issue for now.) To formalise this, we define the first-order language
to be the language generated from
and the rules of propositional grammar by imposing one additional rule:
- If
is a sentence in
, and
is a knowledge agent, then
is a sentence in
(which can informally be read as “
knows (or believes)
to be true”).
Thus, for instance,
is a sentence in ; in the islander interpretation, this sentence denotes the assertion that
knows
to have blue eyes, and
knows that at least one islander has blue eyes, but
does not have blue eyes. On the other hand,
is not a sentence in , because
is not a sentence in
. (However, we will be able to interpret
in the second-order epistemic language
that we will define later.)
We give all the rules of syntax that
presently enjoys. For instance, thanks to modus ponens, we have
Similarly, if are sentences in
such that
, then one automatically has
.
However, we would like to add some additional inference rules to reflect our understanding of what “knowledge” means. One has some choice in deciding what rules to lay down here, but we will only add one rule, which informally reflects the assertion that “all knowledge agents are highly logical”:
- First-order epistemic inference rule: If
are sentences such that
and
is a knowledge agent, then
(We will introduce higher order epistemic inference rules when we turn to higher order epistemic logics.)
Informally speaking, the epistemic inference rule asserts that if can be deduced from
, and
knows
to be true, then
must also know
to be true. For instance, since modus ponens gives us the inference
we therefore have, by the first-order epistemic inference rule,
(note how this is different from (1) – why?).
Another example of more relevance to the islander puzzle, we have
and thus, by the first-order epistemic inference rule,
In the islander interpretation, this asserts that if knows that one of the three islanders
has blue eyes, but also knows that
and
do not have blue eyes, then
must also know that he himself (or she herself) has blue eyes.
One particular consequence of the first-order epistemic inference rule is that if a sentence is a tautology in
– true in every model of
, or equivalently (by completeness) deducible from the inference rules of
, and
is a knowledge agent, then
is a tautology in
:
implies
. Thus, for instance, we have
, because
is a tautology in
(thus
).
It is important to note, however, that if a statement is not a tautology, but merely true in the “real” world
, this does not imply that
is also true in the real world: as we shall see later,
does not imply
. (We will define what
means presently.) Intuitively, this reflects the obvious fact that knowledge agents need not be omniscient; it is possible for a sentence
to be true without a given agent
being aware of this truth.
In the converse direction, we also allow for the possibility that is true in the real world, without
being true in the real world, thus it is conceivable that
is true but
is false. This reflects the fact that a knowledge agent may in fact have incorrect knowledge of the real world. (This turns out not to be an important issue in the islander puzzle, but is of relevance for the unexpected hanging puzzle.)
In a related spirit, we also allow for the possibility that and
may both be true in the real world; an agent may conceivably be able to know inconsistent facts. However, from the inference
of ex falso quodlibet and the first-order epistemic inference rule, this would mean that
is true in this world for every
in
, thus this knowledge agent believes absolutely every statement to be true. Again, such inconsistencies are not of major relevance to the islander puzzle, but as we shall see, their analysis is important for resolving the unexpected hanging puzzle correctly.
Remark 1 It is perhaps worth re-emphasising the previous points. In some interpretations of knowledge,
means that
has somehow been “justified” to be true, and in particular
should entail
in such interpretations. However, we are taking a more general (and abstract) point of view, in which we are agnostic as regards to whether
represents necessary or justified knowledge. In particular, our analysis also applies to “generalised knowledge” operators, such as “belief”. One can of course specialise this general framework to a more specific knowledge concept by adding more axioms, in which case one can obtain sharper conclusions regarding the resolution of various paradoxes, but we will work here primarily in the general setting.
Having discussed the language and syntax of the first-order epistemic logic , we now turn to the semantics, in which we describe the possible models
of
. As
is an extension of
, any model
of
must contain as a component a model
of
, which describes the truth assignment of each of the atomic propositions
of
; but it must also describe the state of knowledge of each of the agents
in this logic. One can describe this state in two equivalent ways; either as a theory
(in
) of all the sentences
in
that
knows to be true (which, by the first-order epistemic inference rule, is closed under
and is thus indeed a theory in
); or equivalently (by the soundness and completeness of
), as a set
of all the possible models of in which all the statements that
knows to be true, are in fact true. We will adopt the latter perspective; thus a model
of
consists of a tuple
where is a model of
, and for each
,
is a set of models of
. To interpret sentences
in
, we then declare
iff
for each atomic sentence
, and declare
iff
is true in every model in
, for each
and
. All other sentences in
are then interpreted by applying the usual truth tables.
As an example of such a model, consider a world with three islanders , each of which has blue eyes, and can each see that each other has blue eyes, but are each unaware of their own eye colour. In this model,
assigns a true value to each of
. As for
, which describes the knowledge state of
, this set consists of two possible
-worlds. One is the “true”
-world
, in which
are all true; but there is also an additional hypothetical
-world
, in which
is true but
is false. With
‘s current state of knowledge, neither of these two possibilities can be ruled out. Similarly,
and
will also consist of two
-worlds, one of which is the “true”
-world
, and the other is not.
In this particular case, the true -world
is included as a possible world in each of the knowledge agents’ set of possible worlds
, but in situations in which the agents knowledge is incorrect or inconsistent, it can be possible for
to not be an element of one or more of the
.
Remark 2 One can view an
model
as consisting of the “real world” – the
-model
– together with
clouds
,
of “hypothetical worlds”, one for each knowledge agent
. If one chooses, one can “enter the head” of any one of these knowledge agents
to see what he or she is thinking. One can then select any one of the
-worlds
in
as a “possible world” in
‘s worldview, and explore that world further. Later on we will iterate this process, giving a tree-like structure to the higher order epistemic models.
Let be the set of all models of
. This is quite a large set; if there are
atomic statements
and
knowledge agents
, then there are
possibilities for the
-world
, and each knowledge agent
has its own independent set
of possible worlds, of which there are
different possibilities, leading to
distinct models
for
in all. For instance, with three islanders wondering about eye colours, this leads to
possibilities (although, once everyone learns each other’s eye colour, the number of possible models goes down quite significantly).
It can be shown (but is somewhat tedious to do so) that the syntax and semantics of the first-order epistemic logic is still sound and complete, basically by mimicking (and using) the proof of the soundness and completeness of
; we sketch a proof of this below when we discuss higher order logics.
— 3. Higher-order epistemic logic —
We can iterate the above procedure and construct a language, syntax, and semantics for order epistemic logic
generated by some atomic propositions
and knowledge agents
, recursively in terms of the preceding epistemic logic
. More precisely, let
be a natural number, and suppose that the logic
has already been defined. We then define the language of
as the extension of
generated by the laws of propositional grammar and the following rule:
- If
is a sentence in
, and
is a knowledge agent, then
is a sentence in
.
Thus, for instance, in the running example of three propositions and three knowledge agents
,
is a sentence in (and hence in
,
, etc.) but not in
.
As for the syntax, we adopt all the inference rules of ordinary propositional logic, together with one new rule:
-
-order epistemic inference rule: If
are sentences such that
and
is a knowledge agent, then
Thus, for instance, starting with
one has
and then
and so forth. Informally, this rule asserts that all agents are highly logical, that they know that all agents are highly logical, and so forth. A typical deduction from these inference rules, which is again of relevance to the islander puzzle, is
Remark 3 This is a very minimal epistemic syntax, and is weaker than some epistemic logics considered in the literature. For instance, we do not have any version of the positive introspection rule
thus we allow the possibility that an agent knows
“subconsciously”, in that the agent knows
but does not know that he or she knows
. Similarly, we do not have any version of the negative introspection rule
so we allow the possibility that an agent is “unaware of his or her own ignorance”. One can of course add these additional rules ex post facto and see how this strengthens the syntax and limits the semantics, but we will not need to do so here.
There is also no reason to expect the knowledge operators to commute:
Now we turn to the semantics. A model of the language
consists of a
-model
, together with sets of possible
-models
associated to their respective knowledge agents
. To describe how
models sentences, we declare
iff
, and for any sentence
in
and
, we declare
iff one has
for every
.
Example 1 We consider an islander model with
atomic propositions
(with each
representing the claim that
has blue eyes) and
knowledge agents
(with
representing the knowledge state of
at a fixed point in time). There are

-models
, determined by the truth values they assign to the
atomic propositions
. For each
, we can then recursively associate a
-model
to each
-model
, by setting
, and then for
, setting
to be the
-model with
-model
, and with
consisting of the pair
, where
(resp.
) is the
-model which is identical to
except that the truth value of
is set to false (resp. true). Informally,
models the
-order epistemology of the
-world
, in which each islander sees each other’s eye colour (and knows that each other islander can see all other islander’s eye colour, and so forth for
iterations), but is unsure as to his or her own eye colour (which is why the set
of
‘s possible
-worlds branches into two possibilities). As one recursively explores the clouds of hypothetical worlds in these models, one can move further and further away from the “real” world. Consider for instance the situation when
and
(thus in the “real” world, all three islanders have blue eyes), and
. From the perspective of
, it is possible that one is in the world
, in which
does not have blue eyes:
. In that world, we can then pass to the perspective of
, and then one could be in the world
, in which neither
nor
have blue eyes:
. Finally, inside this doubly nested hypothetical world, one can consider the perspective of
, in which one could be in the world
, in which none of
have blue eyes:
. This is the total opposite of the “real” model
, but cannot be ruled out in at this triply nested level. In particular, we have
despite the fact that
and
and
for all
. (In particular, the statement
, which asserts “at least one islander has blue eyes”, is not common knowledge in
.
We have the basic soundness and completeness properties:
Proposition 2 For each
,
is both sound and complete.
Proof: (Sketch) This is done by induction on . For
, this is just the soundness and completeness of propositional logic. Now suppose inductively that
and the claim has already been proven for
. Soundness can be verified as in the propositional logic case (with the validity of the
epistemic inference rule being justified by induction). For completeness, one again uses the trick of passing to a maximal
-theory
that contains one set
of sentences in
, but not another sentence
. This maximal
-theory
uniquely determines an
-model
by inspecting whether each
or its negation lies in the theory, and also determines
-theories
for each
. By induction hypothesis, each of these theories can be identified with a collection
of
-models, thus creating a
-model
that obeys
but not
, giving (the contrapositive of) completeness.
— 4. Arbitrary order epistemic logic —
An easy induction shows that the order logic
extends the previous logic
, in the sense that every sentence in
is a sentence in
, every deduction on
is also a deduction in
, and every model of
projects down (by “forgetting” some aspects of the model) to a model of
. We can then form a limiting logic
, whose language is the union of all the
(thus,
is a sentence in
iff
lies in
for some
), whose deductive implications are the union of all the
deductive implications (thus,
if we have
for some
), and whose models are the inverse limits of the
models (thus, a model
of
is an infinite sequence of models
of
for each
, such that each
projects down to
for
. It is not difficult to see that the soundness and completeness of each of the
implies the soundness and completeness of the limit
(assuming the axiom of choice, of course, in our metamathematics).
The logic now allows one to talk about arbitrarily deeply nested strings of knowledge: if
is a sentence in
, and
is a knowledge agent, then
is also a sentence in
. This allows for the following definition:
Definition 3 (Common knowledge) If
is a sentence in
, then
is the set of all sentences of the form
where
and
are knowledge agents (possibly with repetition).
Thus, for instance, using the epistemic inference rules, every tautology in is commonly known as such: if
, then
.
Let us now work in the islander model in which there are atomic propositions
and
knowledge agents
. To model the statement that “it is commonly known that each islander knows each other islander’s eye colour”, one can use the sets of sentences
for all distinct .
For any , let
denote the sentence that there are at least
blue-eyed islanders; this can be encoded as a suitable finite combination of the
. For instance,
can be expressed by any tautology,
can be expressed by
,
can be expressed by
, and intermediate
can be expressed by more complicated formulae. Let
denote the statement that there are exactly
blue-eyed islanders; for instance, if
, then
can be expressed as
The following theorem asserts, roughly speaking, that if there are blue-eyed islanders, and it is commonly known that there are at least
blue-eyed islanders, then all blue-eyed islanders can deduce their own eye colour if
, but not otherwise.
Theorem 4 Let
be the set of sentences consisting of the union of (2) and (3) for all distinct
. Let
. Let
denote the sentence
(informally,
asserts that all blue-eyed islanders know their own eye colour).
- If
, then
- If
, then
Proof: The first part of the theorem can be established informally as follows: if holds, then each blue-eyed islander sees
other blue-eyed islanders, but also knows that there are at least
blue-eyed islanders. If
, this forces each blue-eyed islander to conclude that his or her own eyes are blue (and in fact if
, the blue-eyed islander’s knowledge is now inconsistent, but the conclusion is still valid thanks to ex falso quodlibet). It is a routine matter to formalise this argument using the axioms (2), (3) and the epistemic inference rule; we leave the details as an exercise.
To prove the second part, it suffices (by soundness) to construct a -model
which satisfies
,
, and
but not
. By definition of an
-model, it thus suffices to construct, for all sufficiently large natural numbers
, an
-model
which satisfies
,
, and
, but not
, and which are consistent with each other in the sense that each
is the restriction of
to
.
We can do this by a modification of the construction in Example 1. For any -model
, we can recursively define an
-model
for any
by setting
, and then for each
, setting
to be the
-model with
-model
, and with possible worlds
given by
this is the same construction as in Example 1, except that at all levels of the recursive construction, we restrict attention to worlds that obey . A routine induction shows that the
determine a limit
, which is an
model that obeys
and
. If
, then clearly
as well. But if
, then we see that
, because for any index
with
, we see that if
, then
contains worlds in which
is false, and so
for any
.
— 5. Temporal epistemic logic —
The epistemic logic discussed above is sufficiently powerful to model the knowledge environment of the islanders in the blue-eyed islander puzzle at a single instant in time, but in order to fully model the islander puzzle, we now must now incorporate the role of time. To avoid confusion, I feel that this is best accomplished by adopting a “spacetime” perspective, in which time is treated as another coordinate rather than having any particularly privileged role in the theory, and the model incorporates all time-slices of the system at once. In particular, if we allow the time parameter to vary along some set
of times, then each actor
in the model should now generate not just a single knowledge agent
, but instead a family
of knowledge agents, one for each time
. Informally,
should then model the assertion that “
knows
at time
“. This of course leads to many more knowledge agents than before; if for instance one considers an islander puzzle with
islanders over
distinct points in time, this would lead to
distinct knowledge agents
. And if the set of times
is countably or uncountably infinite, then the number of knowledge agents would similarly be countably or uncountably infinite. Nevertheless, there is no difficulty extending the previous epistemic logics
and
to cover this situation. In particular we still have a complete and sound logical framework to work in.
Note that if we do so, we allow for the ability to nest knowledge operators at different times in the past or future. For instance, if we have three times , one could form a sentence such as
which informally asserts that at time ,
knows that
already knew
to be true by time
, or
which informally asserts that at time ,
knows that
will know
to be true by time
. The ability to know certain statements about the future is not too relevant for the blue-eyed islander puzzle, but is a crucial point in the unexpected hanging paradox.
Of course, with so many knowledge agents present, the models become more complicated; a model of
now must contain inside it clouds
of possible worlds for each actor
and each time
.
One reasonable axiom to add to a temporal epistemological system is the ability of agents to remember what they know. More precisely, we can impose the “memory axiom”
for any , any
, and any
. (This axiom is important for the blue-eyed islander puzzle, though it turns out not to be relevant for the unexpected hanging paradox.)
We can also define a notion of common knowledge at a single time : given a sentence
, we let
denote the set of sentences of the form
where and
. This is a subset of
, which is the set of all sentences of the form
where can vary arbitrarily in
.
— 6. The blue-eyed islander puzzle —
Now we can model the blue-eyed islander puzzle. To simplify things a bit, we will work with a discrete set of times indexed by the integers, with
being the day in which the foreigner speaks, and any other time
being the time
days after (or before, if
is negative) the foreigner speaks. (One can also work with a continuous time with only minor changes.) Note the presence of negative time; this is to help resolve the question (which often comes up in discussion of this puzzle) as to whether the islanders would already have committed suicide even before the foreigner speaks.
Also, the way the problem is set up, we have the somewhat notationally annoying difficulty that once an islander commits suicide, it becomes meaningless to ask whether that islander continues to know anything or not. To resolve this problem, we will take the liberty of modifying the problem by replacing “suicide” with a non-lethal public ritual. (This means (thanks to (4)) that once an islander learns his or her own eye colour, he or she will be condemned to repeating this ritual “suicide” every day from that point.) It is possible to create a logic which tracks when different agents are alive or dead and to thus model the concept of suicide, but this is something of a distraction from the key point of the puzzle, so we will simply redefine away this issue.
For similar reasons, we will not concern ourselves with eye colours other than blue, and only consider suicides stemming from blue eyes, rather than from any non-blue colour. (It is intuitively obvious, and can eventually be proven, that the foreigner’s statement about the existence of blue-eyed islanders is insufficient information to allow any islander to distinguish between, say, green eyes and brown eyes, and so this statement cannot trigger the suicide of any non-blue-eyed person.)
As in previous sections, our logic will have the atomic propositions , with each
expressing the statement that
has blue eyes, as well as knowledge agents
for each
and
. However, we will also need further atomic propositions
for
and
, which denote the proposition that
commits suicide (or a ritual equivalent) at time
. Thus we now have a countably infinite number of atomic propositions and a countably infinite number of knowledge agents, but there is little difficulty extending the logics
and
to cover this setting.
We can now set up the various axioms for the puzzle. The “highly logical” axiom has already been subsumed in the epistemological inference rule. We also impose the memory axiom (4). Now we formalise the other assumptions of the puzzle:
- (All islanders see each other’s eye colour) If
are distinct and
, then
and - (Anyone who learns their own eye colour is blue, must commit suicide the next day) If
and
, then
- (Suicides are public) For any
,
, and
, we have
Similarly, if, then
- (Foreigner announces in public on day 0 that there is at least one blue-eyed islander) We have
Let denote the union of all the axioms (4), (5), (6), (7), (8), (10). The “solution” to the islander puzzle can then be summarised as follows:
Theorem 5 Let
.
- (At least one blue-eyed islander commits suicide by day
)
- (Nobody needs to commit suicide before day
) For any
and
,
The first conclusion is weaker than the “Solution 2″ of the puzzle, which would assert in fact that all blue-eyed islanders will commit suicide on day
. While this indeed the “default” outcome of the hypotheses
, it turns out that this is not the only possible outcome; for instance, if one blue-eyed person happens to commit suicide on day
or day
(perhaps for an unrelated reason than learning his or her own eye colour), then it turns out that this “cancels” the effect of the foreigner’s announcement, and prevents further suicides. (So, strictly speaking, Solution 2 is not quite accurate, though it is much closer to the truth than Solution 1 is.)
In fact there is a strengthening of the first conclusion: given the hypotheses , there must exist a time
and
distinct islanders
such that
holds for all
.
Note that the second conclusion does not prohibit the existence of some models of in which suicides occur before day
(consider for instance a situation in which a second foreigner made a similar announcement a few days before the first one, causing the chain of events to start at an earlier point and leading to earlier suicides).
Proof: (Sketch) To illustrate the first part of the theorem, we focus on the simple case ; the general case is similar but requires more notation (and an inductive argument). It suffices to establish that
(i.e. if nobody suicides by day , then both islanders will suicide on day
.)
Assume . From (10) we have
and hence by (4)
By (6) we also have
whereas from the epistemic inference axioms we have
From the epistemic inference axioms again, we conclude that
and hence by (7) (and epistemic inference)
On the other hand, from and (9) we have
and hence by epistemic inference
and thus by (7)
A similar argument gives , and the claim follows.
To prove the second part, one has to construct, for each , an
-model in which
is true and
is false for any
and
. This is remarkably difficult, in large part due to the ability of nested knowledge operators to jump backwards and forwards in time. In particular, one can jump backwards to before Day 0, and so one must first model worlds in which there is no foreigner announcement. We do this as follows. Given an
-model
, we recursively define a
-model
for
as follows. Firstly,
. Next, if
and
has already been defined, we define
to be the
-model with
-model
, and for any
and
, setting
to be the set of all
-models of the form
, where
is an
-model obeying the following properties:
- (
sees other islanders’ eyes) If
and
, then
iff
.
- (
remembers suicides) If
and
, then
iff
.
Now we model worlds in which there is a foreigner announcement. Define an admissible model to be an
-model
such that there exist
for which the following hold:
-
(i.e. there are exactly
blue-eyed islanders in the world
).
- There exists distinct
such that
and
for all
.
- For any
and
,
implies
.
We call the blue-eyed count of
.
(Such models, incidentally, can already be used to show that no suicides necessarily occur in the absence of the foreigner’s announcement, because the limit of such models always obey all the axioms of
except for (10).)
Given an admissible -model
of some blue-eyed count
, we recursively define an
model
for
by setting
, then if
and
has already been defined, we define
to be the
-model with
-model
, and with
for
and
defined by the following rules:
Case 1. If , then we set
to be the set of all
-models of the form
, where
obeys the two properties “
sees other islanders’ eyes” and “
remembers suicides” from the preceding construction. (
does not need to be admissible in this case.)
Case 2. If ,
, and there does not exist
distinct
such that
for all
, then we set
-models of the form
, where
is admisssible, obeys the two properties “
sees other islanders’ eyes” and “
remembers suicides” from the preceding construction, and also obeys the additional property
. (Informally, this is the case in which
“must learn”
.)
Case 3. In all other cases, we set to be the set of all
-models of the form
, where
is admissible and obeys the two properties “
sees other islanders’ eyes” and “
remembers suicides” from the preceding construction.
We let be the limit of the
(which can easily be verified to exist by induction). A quite tedious verification reveals that for any admissible
-model
of blue-eyed count
, that
obeys both
and
, but one can choose
to not admit any suicides before time
, which will give the second claim of the theorem.
Remark 4 Under the assumptions used in our analysis, we have shown that it is inevitable that the foreigner’s comment will cause at least one death. However, it is possible to avert all deaths by breaking one or more of the assumptions used. For instance, if it is possible to sow enough doubt in the islanders’ minds about the logical and devout nature of the other islanders, then one can cause a breakdown of the epistemic inference rule or of (7), and this can prevent the chain of deductions from reaching its otherwise deadly conclusion.
— 7. The unexpected hanging paradox —
We now turn to the unexpected hanging paradox, and try to model it using (temporal) epistemic logic. (For a formulation of this paradox, I will refer to the Wikipedia entry for this paradox.)
It turns out that there are several, not quite equivalent, ways to model this “paradox” epistemologically, with the differences hinging on how one interprets what “unexpected” or “surprise” means. In particular, if is a sentence and
is a knowledge agent, how would one model the sentence “
does not expect
” or “
is surprised by
“?
One possibility is to model this sentence as
i.e. as the assertion that does not know
to be true. However, this leads to the following situation: if
has inconsistent knowledge (in particular, one has
, where
represents falsity (the negation of a tautology)), then by ex falso quodlibet,
would be true for every
, and hence
would expect everything and be surprised by nothing. An alternative interpretation, then, is to adopt the convention that an agent with inconsistent knowledge is so confused as to not be capable of expecting anything (and thus be surprised by everything). In this case, “
does not expect
” should instead be modeled as
i.e. that either does not know
to be true, or is inconsistent.
Both interpretations (11), (12) should be compared with the sentence
i.e. that knows that
is false. If
is consistent, (13) implies (11), but if
is inconsistent then (13) is true and (11) is false. In either case, though, we see that (13) implies (12).
Let now analyse the unexpected hanging paradox using the former interpretation (11) of surprise. We begin with the simplest (and somewhat degenerate) situation, in which there is only one time (say Monday at noon) in which the hanging is to take place. In this case, there is just one knowledge agent (the knowledge of the prisoner after the judge speaks, but before the executation date of Monday at noon). We introduce an atomic sentence
, representing the assertion that the prisoner will be hanged on Monday at noon. In this case (and using the former interpretation (11) of surprise), the judge’s remarks can be modeled by the sentence
The “paradox” in this case stems from the following curious fact:
- There exist
-models in which
is true.
- There exist
-models in which
is true.
- However, there does not exist any
-model in which both
and
is true.
Thus, the judge’s statement can be true, but if so, it is not possible for the prisoner to know this! (In this regard, the sentence is analogous to a Godel sentences, which can be true in models of a formal system, but not provable in that system.) More informally: knowing a surprise, ruins that surprise.
Proof: The third statement is easy enough to establish: if is true in some model, then clearly
is true in that model; but if
is true in the same model, then (by epistemic inference)
will be true as well, which is a contradiction.
The first statement is also fairly easy to establish. We have two -models; a model
in which
is true, and a model
in which
is false. We can recursively define the
-model
for any
and any
by setting
, and for
, setting
to be the
-model with
-model
, and with
. One then easily verifies that the
have a limit
, and that
models
(but not
, of course).
A trivial way to establish the second statement is to make a model in which is inconsistent (thus
is empty). One can also take
to be
, and this will also work. (Of course, in such models,
must be false.)
Another peculiarity of the sentence is that
as can be easily verified (by modifying the proof of the second statement of the above theorem). Thus, the sentence has the property that if the prisoner believes
, and also knows that he or she believes
, then the prisoner’s beliefs automatically become inconsistent – despite the fact that
is not actually a self-contradictory statement (unless also combined with
).
Now we move to the case when the execution could take place at two possible times, say Monday at noon and Tuesday at noon. We then have two atomic statements: , the assertion that the execution takes place on Monday at noon, and
, the assertion that the execution takes place on Tuesday at noon. There are two knowledge agents;
, the state of knowledge just before Monday at noon, and
, the state of knowledge just before Tuesday at noon. (There is again the annoying notational issue that if
occurs, then presumably the prisoner will have no sensible state of knowledge by Tuesday, and so
might not be well defined in that case; to avoid this irrelevant technicality, we replace the execution by some non-lethal punishment (or use an alternate formulation of the puzzle, such as the surprise exam formulation).)
We will need one axiom beyond the basic axioms of epistemic logic, namely
Thus, it is common knowledge that if the execution does not happen on Monday, then by Tuesday, the prisoner will be aware of this fact. This axiom should of course be completely non-controversial.
The judge’s sentence, in this case, is given by
Analogously to Theorem 6, we can find models obeying (14) in which
is true, but one cannot find models obeying (14) in which
,
,
, and
are all true, as one can soon see that this leads to a contradiction. Indeed, from
one has
while from (14) one has
and from one has
wihch shows that leads to a contradiction, which implies
and hence
by
. On the other hand, from
one has
while from (14) one has
and from one has
which shows that , and thus
, a contradiction. So, as before,
is a secret which can only be true as long as it is not too widely known.
A slight variant of the above argument shows that if ,
, and
hold, then
and
hold – or informally, the prisoner can deduce using knowledge of
(and knowledge of knowledge of
) that there will be no execution on either date. This may appear at first glance to be consistent with
(which asserts that the prisoner will be surprised when the execution does happen), but this is a confusion between (11) and (13). Indeed, one can show under the assumptions
that
is inconsistent, and (if
holds) then
is also inconsistent, and so
and
do not, in fact, imply
.
Now suppose that we interpret surprise using (12) instead of (11). Let us begin first with the one-day setting. Now the judge’s sentence becomes
In this case it is possible for and
to be true, and in fact for
to be common knowledge, basically by making
inconsistent. (A little more precisely: we use the
-model
where
and
. Informally: the judge has kept the execution a surprise by driving the prisoner insane with contradictions.
The situation is more interesting in the two-day setting (as first pointed out by Kritchman and Raz), where is now
Here it is possible for to in fact be common knowledge in some
-model, but in order for this to happen, at least one of the following three statements must be true in this model:
-
.
-
.
-
.
(We leave this as an exercise for the interested reader.) In other words, in order for the judge’s sentence to be common knowledge, either the prisoner’s knowledge on Monday or Tuesday needs to be inconsistent, or else the prisoner’s knowledge is consistent, but the prisoner is unable (on Monday) to determine that his or her own knowledge (on Tuesday) is consistent. Notice that the third conclusion here is very reminiscent of Gödel’s second incompleteness theorem, and indeed in the above-mentioned paper of Kritchman and Raz, the surprise examination argument is modified to give a rigorous proof of that theorem.
Remark 5 Here is an explicit example of a
-world in which
is common knowledge, and
and
are both consistent (but
does not know that
is consistent). We first define
-models
for each
recursively by setting
to be the world in which
and
, and then define
for
to be the
-model with
-model
, with
, and
. (Informally: the execution is on Tuesday, and the prisoner knows this on Monday, but has become insane by Tuesday.) We then define the models
for
recursively by setting
to be the world in which
and
, then define
for
to be the
-model with
-model
,
, and
. (Informally: the execution is on Monday, but the prisoner only finds this out after the fact.) The limit
of the
then has
as common knowledge, with
and
both false, but
is also false.

54 comments
Comments feed for this article
22 May, 2011 at 1:54 am
astrolemei
I don’t know why, but this article does not show up in my Google Reader update, while the one before and the one after this article both show up.
23 May, 2011 at 1:48 pm
Pace Nielsen
On the unexpected hanging paradox, aka the surprise-exam paradox: The beauty of the paradox is that it is phrased in terms of real-life situations, where the teacher states something as true, the student tries to work via proof by contradiction to refute the statement, believes he has done so, and then the statement still is true.
In the *initial* formulation of the paradox by Kritchman and Raz paper, their resolution is that the teacher’s statement was simply a contradiction. However, that is not satisfying because those reading the problem see that the teacher did not lie. The students *were* surprised, just as she said. The teacher’s statement only becomes a lie when we equate being surprised with provability, and that throws into question the idea of making them equivalent in our formulation.
Kritchman and Raz then try to modify the teacher’s sentence to make it a non-contradiction, but in doing so they don’t address the the inadequacy of their initial formulation. Further, while possessing interesting properties (some of which you explain in your post above), the new formulation doesn’t seem to be natural or really contain the paradox anymore. Would we find it puzzling to be given a self-referential formal sentence which tells us we cannot prove something using that sentence? Not really.
But I think that both of those formulations hide a much simpler resolution to the paradox. Namely, the student, along with Kritchman and Raz, are committing a modal fallacy: http://www.sfu.ca/~swartz/modal_fallacy.htm They are interpreting the judge’s statement as a statement about the future which must *necessarily* be true. They make it an axiom. But think about it. If we change the teacher’s words to reflect this understanding — if she were to say something like “There is no way you won’t be surprised by your test.” the game-theorists among us would say “Well, I’ll just plan on being tested every day.” The teacher’s statement would be false, and this would be evidenced by us when we prepare for a test each morning. (We wouldn’t be like the student in the example, and let our guard down, thinking we had already refuted the teacher.)
But if the teacher merely asserted (because, of course, no real teacher could assert absolute knowledge of what you will do) that you will be surprised when you are tested, and we understand that the teacher was merely voicing her opinion, it becomes clear what the student’s mistake was. He was reading the teachers statement as one of necessity, when it was not so.
So, in summary, while it makes sense to interpret the statement made by the visitor to the island as an commonly known axiom that must hold true in all possible worlds; doing so in the surprise-test paradox is making the same mistake as the student.
23 May, 2011 at 2:17 pm
Terence Tao
Yes, one can certainly interpret the surprise examination without paradox if one interprets surprise using the necessary modal operator, i.e. “the student will be surprised by X” is interpreted as “the student knows that X is necessarily false” (or, the subtly different “the student does not necessarily know that X is true”), and then the resolution is that the teacher’s statement is not known to be necessarily true. But this is only one of several possible ways to interpret the paradox; one could instead interpret surprise in terms of belief, i.e. “the student will be surprised by X” means that “the student believes that X is false” (or, the subtly different “the student does not believe that X is true”). The teacher’s statement is certainly believable, and so one needs a different resolution to the paradox in this case. (For instance, one can resolve the paradox by noting that the teacher’s statement can be true, but it cannot be believed by the student without causing an inconsistency in that student’s belief system; this is the resolution I prefer in my post above (the epistemic logic I use works just as well for belief as it does for knowledge). Kritchman and Raz have a slightly different formulation in which one possible resolution comes from the fact that a student cannot consistently believe that his or her future beliefs are consistent, while also believing statements about the future such as the teacher’s statement.)
23 May, 2011 at 4:51 pm
Koray
I don’t think we should be looking for ways to be able to still “interpret” this as a paradox. The only way this would be a “paradox” is when the judge/teacher does not mislead, the student/prisoner is not inconsistent and the definition of K is surprised is: A is true and K(not A).
If the student can hold unsupported beliefs or the teacher can lie, I have trouble explaining to anyone why this problem is interesting.
Thanks for the excellent post.
23 May, 2011 at 9:26 pm
Pace Nielsen
I see a large difference between the words “belief” and “knowledge.” For instance, I view belief as more fluid, and more under our control, and would be opposed to axiom (4) on that (and other grounds) with respect to belief. But since your original post uses the term knowledge, as does the Kritchman and Raz paper, I’ll try to stick with that word. If you want to separate your view from the one in that paper– that knowledge and provability can be interchanged–just let me know and I’ll switch gears.
In your post you say: “Here it is possible for {S} to in fact be common knowledge in some {L_\infty}-model…” and in your response to me you say “The teacher’s statement is certainly believable, and so one needs a different resolution to the paradox in this case. ” The trouble is, I don’t believe the teacher’s statement is necessarily true. Even in the phrasing used by Kritchman and Raz, if I’m parsing it correctly, T+S is consistent if and only if T+ not(S) is consistent. The student in the paradox ultimately does not believe the teacher either even though, in that particular world, the teacher is correct. If S were common knowledge, the student would have no reason to search for a contradiction. It would be futile. Thus, if we are only looking at models where S is common knowledge then that is, in my opinion, fundamentally changing what the paradox is talking about.
As an easy fix, we might say we don’t assume S is common knowledge. Instead, the student just looks at the possible worlds where S is true, and tries to find a contradiction in them all, and thus he will know either his own world is inconsistent or S is false. This seems to match what is happening in the original wording. The trouble is, in some of those possible worlds he does not know S is true (such as in the world he actually lives in). So whatever his logic, he cannot assume K(S) in that world either. He can merely assume S. [Note: Such a blunder would be another type of modal error, thinking of K as a modal operator.]
Let’s assume our student does not make that error, and does not assume K(S). Let’s also look with our student at a world M where S is true and E_1 is true. Let’s further say this is the real world for simplicity (and to match what actually happens in the paradox), although the student doesn’t know this. Well, since S is true, the student in that possible world, at time 1, does not know that E_1 is true. If we try to translate the original wording of the student’s logic into this framework, it immediately falls apart, because even if K_2(E_2) is false, in the world M, K_1 does not know that K_2(E_2) is false, in fact he does not believe (let alone know) that S is true (even though it is). Notice that this is exactly what happens in the real world. Further note that the error in E_1’s logic is not in some tacit assumption that he will only know true things in the future, but rather in an incorrect use of logic to come to the conclusion K_1(not(K_2(E_2))) in M (or K(S) in M).
24 May, 2011 at 8:03 am
Terence Tao
As I said in my reply to Jordan below, I’m working in an abstract generalised framework in which one can take an agnostic position as to whether K represents knowledge, belief, necessary truth, empirical knowledge, or any other knowledge-like operator. In this abstract setting, what one can show in general (using the first interpretation (11) of surprise) is that the judge’s statement S cannot be commonly known to be true, or (using the second interpretation (12) of surprise) that if S to be commonly known, then either K_1 or K_2 is inconsistent, or K_1 does not know that K_2 is consistent.
One can then specialise this abstract result to more specific interpretations of knowledge and get a simpler conclusion. In particular, if K represents necessary knowledge, then the conclusion is simply (as you say) that S is not knowable (in the first interpretation, at least); and if K represents provability, then (using the second interpretation) Kritchman and Raz obtain a rigorous proof of the second incompleteness theorem. In a belief model of knowledge, the conclusion is that believing S (and also believing that one believes S) leads to inconsistency in one’s beliefs.
Incidentally, the memory axiom (4) is needed in a crucial way for the islander puzzle, but not for the surprise paradox (basically because the deductive chain of reasoning moves forwards in time in the former, but backwards in time in the latter), and so one can safely omit this axiom if desired if one is only interested in treating the surprise paradox. (I’ll update the text to clarify this point.)
24 May, 2011 at 8:51 am
Pace Nielsen
I think I understood all of this. I also hope it was clear that I had allowed an expansive view of the K operator in my response. And it *is* neat that S has such interesting properties, although there are simpler sentences with one or all of these properties, such as: “You will not have consistent beliefs.”
But the point that I’m contending (hopefully in a non-contentious was) is that none of those facts has any bearing on the actual surprise examination paradox. There is no reason to assume the teacher’s statement as either axiomatic or common knowledge. We, the readers, already understand that the teacher/judge’s statement should be taken with a grain of salt. The response of the student/criminal shows us that much; he doesn’t believe it either. Any analysis of what happens when assuming C(S) is besides the point. The only way we might want to start assuming C(S) is if we think the teacher has some added information about the student (e.g., knows he is bad at logic), but then we cannot identify with the student in the paradox. For the power in the paradox is that the student’s logic is initially appealing. We want to put ourselves in his/her shoes and work it out ourselves.
So it is interesting to discuss what happens when one assumes S is common knowledge, but that is besides the point with regards to the resolution of the paradox itself (unless you interpret the student/criminal’s argument as implicitly assuming C(S); but then the resolution is simply that this should not have been assumed by the student, *especially* since the student does not believe S!).
24 May, 2011 at 9:22 am
Pace Nielsen
That first sentence should be “If you believe this sentence, you will not have consistent beliefs.” Or something like that.
3 February, 2012 at 4:21 pm
Paul
“…the game theorists among us…” brings to mind an unpublished idea of Karl Narveson mentioned in http://www-math.mit.edu/~tchow/unexpected.pdf. “The teacher ’s goal is to
find a probability distribution that maximizes the absolute value of the expected surprise when the quiz is announced. Here “surprise” is based on Shannon entropy…” (Back in the ’80s I sent a similar formulation to Douglas R. Hofstadter’s “Metamagical Themas” column.) The fact that the optimal strategies for both the students and the teacher are not pure corresponds directly to (and quantifies) the consistency (or lack thereof) of the students’ beliefs and the teacher’s assertion.
23 May, 2011 at 6:20 pm
JSE
Very interesting, Terry!
A traditional view among epistemologists — and one which I think remains widely held — is that knowledge is “justified true belief.” In particular, I think many philosophers would call your K operator something other than “knowledge” since you don’t want K(S) to entail S. Perhaps they would like to call it “belief,” or some unnamed intermediate value between “belief” and “knowledge?”
If you ask K(S) to entail S, then in the unexpected hanging situation I think one is forced to conclude that it is _impossible_ to know (in the “justified true belief” sense) that the hanging will be unexpected.
24 May, 2011 at 7:30 am
Terence Tao
Ah, I see that my choice of terminology (and my minimalistic choice of axioms) here has caused some confusion. Perhaps I would term my operators K “generalised knowledge operators”; they could represent knowledge in the “justified true belief” sense (or the more formal sense of “provability” as used by Kritchman and Raz), or they could represent knowledge in the empirical sense (obtained from (non-mathematical) inductive reasoning, for instance), or belief, but I deliberately chose to be agnostic as to which interpretation to assign to K, so that the abstract analysis I give here could be applicable to a variety of interpretations. I’ll update the text to clarify this point.
As such, I view the surprise paradox as having a number of distinct formulations (depending on one’s interpretation of K, and one’s interpretation of “surprise”), and each has a slightly different resolution, somewhat analogously to how, say, Russell’s paradox, has a number of distinct formulations and resolutions depending on the set theory one wishes to work in. In those interpretations in which knowledge is necessarily true, and commonly known to be such (thus, in my notation,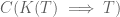 for all T and K), the resolution is indeed that the judge/teacher’s statement S is unknowable; the standard of knowledge here is simply too high to admit this statement as necessary truth, no matter how reliable or trustworthy the judge/teacher is.
for all T and K), the resolution is indeed that the judge/teacher’s statement S is unknowable; the standard of knowledge here is simply too high to admit this statement as necessary truth, no matter how reliable or trustworthy the judge/teacher is.
As pointed out by several commenters, with this interpretation the paradox is no longer particularly impressive, as we are accustomed to not giving the proclamation of any authority the status of necessary truth. (A somewhat topical possible counterexample, incidentally, is the version of S found in Matthew 24:36: “No man knows the day or hour [of Christ’s return]”, though the interpretation of this sentence is subject to dispute, to put it mildly. Still, it is amusing to note that under some interpretations at least of knowledge, of S, and of the authority of the Bible, we obtain as a corollary of the surprise paradox argument that no man can obtain any finite upper bound of the day or hour of Christ’s return either.)
More interesting, in my view, is an empirical interpretation of knowledge; for instance, a model in which K(S) is true if S has been observed empirically in a large number of previous instances.
One can then imagine a scenario in which the surprise exam is conducted over and over again, with the hapless student always concluding that no exam can occur, and being surprised every time. In this case, what happens is that one’s empirical knowledge can lead to inconsistency. While this is not a novel observation (cf. the grue paradox), it is a somewhat “non-artificial” demonstration of this fact (analogously to how Goedel’s second incompleteness theorem demonstrates the undecidability of a “non-artificial” sentence – namely, consistency – in contrast to the first incompleteness theorem, in which the undecidable statement is clearly artificial.)
25 May, 2011 at 5:29 am
JSE
Once you have gone this far it seems natural to go all the way and model degrees of belief — i.e. to have, for each d in [0,1] an operator K_d(S) modeling “knowledge agent has degree of belief d in S,” or perhaps “has degree of belief at least d in S.” My sense is that even propositional logic runs into trouble when you try to introduce propositions whose truth is uncertain, so perhaps there are insuperable difficulties here. On the other hand, perhaps quarantining all uncertainties into statements about belief defuses problems which look difficult when we try to interpret them as uncertainty about actual truth.
Without something like this I worry that the “empirically supported belief” model will be vulnerable to sorites problems, where it is hard to see how “one more observation” can change K(S) from false to true.
25 May, 2011 at 3:50 pm
Terence Tao
Ah, that is an interesting way to model belief. It is true that the solution to the islander puzzle starts collapsing if, say, each islander has only a 99% confidence in the logical and devout nature of the other islanders (or is only 99% confident that they heard the foreigner speak, etc.), and if islanders only commit suicide if they have, say, 90% or more confidence in their own eye colour. One can then imagine the solution holding up for small numbers of blue-eyed islanders but not for larger ones as the confidence will start decreasing as one stacks more and more 99% implications in one’s deductive chain of reasoning.
The surprise paradox seems to similarly disappear if one makes any pronouncement about a certain degree of belief, less certain than the belief in question. For instance, if a judge asserts that one will not be able to expect the hanging with 99% confidence, one might only rate this statement with a 98% confidence of correctness. In such an event, one cannot obtain any sort of contradiction or inconsistency even if the judge’s statement is commonly known.
It does seem quite hard to model this type of approximate belief rigorously, though. Bayesian probability is presumably the way to go, but one has to be careful to avoid self-referentiality.
24 May, 2011 at 2:11 am
plm
Seeing the number of comments on the previous blue eyed posts I am pretty sure a few will be disappointed at the length and complexity of this one. At least if they read that “Solution 2 is not quite accurate” there.
This may hurt sensibilities. And, if I understand correctly, if Solution 2 fails it is because t islanders commit suicide on day t<m for some other reason. But for puzzling sake we could arguably assume that islanders do not behave unpredictably, at least adding the axiom that they only commit suicide day t+1 if they know their eyes blue (a left-right arrow in (7)).
Thank you for the very nice post.
24 May, 2011 at 6:56 am
Terence Tao
Yes, this is the reason why Solution 2 is only accurate in a “default” sense. Unfortunately, it is difficult to formalise “do not behave unpredictably”, even if one makes (7) an if-and-only-if, it is still possible for the islanders to have access to external sources of knowledge (e.g. mirrors) that could lead one or more islanders to deduce their eye colour prematurely. (The puzzle does explicitly rule out reflective surfaces in the informal wording, but it is difficult to formalise this hypothesis in an epistemological model.) The best I can do is to come up with a model of the puzzle in which the suicides do indeed happen on the 100th day, showing that the outcome of Solution 2 is _possible_, but not _necessary_.
I did think about making a simplified version of this post purely for the purposes of “solving” the blue-eyed islander puzzle, but ultimately I decided that this would “spoil” the puzzle too much, and if were not completely formalised, it probably would not conclusively settle all doubt.
EDIT: Actually, I suppose in this case one can actually formalise the “do not behave unpredictably” assumption as follows. Call a model of an epistemic theory _minimal-knowledge_ if the only knowledge that any agent has is that knowledge which is necessarily true in all models of that theory. It seems to me that the assumptions of the blue-eyed islander puzzle are closed under intersection of knowledge, and as such, a minimal-knowledge model exists. In that model, at least, there will be no suicides until the 100th day (assuming (7) is now an if and only if).
24 May, 2011 at 11:37 am
plm
This looks like a great solution, formalizing the appearance of a second (nth?) concept of completeness in epistemic logic.
Sorry that I was mistaken on my proposed amendment.
I will probably be mistaken again, but I think I should still post the following proposals.
1. Adding another rule, the converse of the rule of epistemic inference -predictability/rationality/… rule?
2. Adding the axiom scheme K_i(\phi)->\phi. (I have serious doubts about this one, but the idea is that islander i should know a fact only if it is provable, so perhaps we need rather add K_i(\phi) for \phi axioms and then finish the definition recursively.)
3. We could look for “minimal” suicide rate models where suicides occur as late as possible. Actually, the later the suicides the more, if I am not mistaken.
6 June, 2011 at 10:50 am
Pace Nielsen
I’m trying to understand your comment about a minimal knowledge model. Let MK be your minimal knowledge model. Let model A be one where one of the islanders was insane and committed suicide early. Let model B be one where the blue-eyed islanders all commit suicide on the last day possible.
In model A there is an islander who knows on day 2 that someone has died (since suicides are public). In model B, that same islander knows that nobody has died (because he knows suicides are public, and he didn’t see any suicide). So, in model MK does that islander know someone has died or not?
[It would be interesting to have a world where that world itself has no impact on your knowledge–rather only the Platonic world of absolutes.]
6 June, 2011 at 11:05 am
Terence Tao
Ah, I think I have to refine the notion of a minimal knowledge model a bit, in that the only k^th order knowledge present in such a world is that which is available in all worlds with the same (k-1)^{th} order knowledge. So one would never intersect world A with world B, because the 0^th order state of these two worlds is different.
With this new definition of minimal knowledge world, though, uniqueness becomes trickier to establish; it is not immediately obvious, for instance, that there is not a MK world in which there is a suicide on the first day, until one can first establish that on the first day in any MK world that no islander knows his or her own eye colour. One may have to “start the clock” at some finite time -N in order to be able to inductively establish uniqueness.
6 June, 2011 at 12:02 pm
Pace Nielsen
I see a possible point of equivocation. Is k the depth on the order of logic (as used in your original post above), or is k the time index? From what you wrote most recently, I think you meant the time index. If I’m wrong, just let me know.
If k is the time index t, I don’t see how starting the clock helps. Your axioms do not force worlds to evolve the same way. For example, for all we know worlds A and B in the example above agree before the first day. (Or, we could modify them slightly to agree on the first day, but diverge on the second day. etc…) And knowledge is affected by what happens in the world in which you live.
As long as your set-up allows for someone to know (or not know) their eye-color on some day for no reason at all, then it will also mean that future states are not *necessary*, they are not determined. Thus opposite states can result from equivalent previous times. When this fact is paired with any axiom which *forces* islanders to know which of the opposite states exists in the actual world in which they live, that will prevent the existence of MK worlds.
6 June, 2011 at 12:42 pm
Terence Tao
Hmm, I guess one would have to use both depth and time ordering together to get a good concept of a MK world, namely that a knowledge agent K in an MK world knows a k^th knowledge order sentence S at time n or before, thus if and only if
if and only if  is also true in all worlds
is also true in all worlds 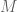 which agree with MK on all sentences of up to k^th knowledge order involving only times up to n. Branching of worlds beyond day n only affects knowledge beyond day n (because, unlike the situation with the surprise paradox, there is no mechanism for knowing anything non-tautological about the future), so this should allow for the existence of an MK world (namely, the “obvious” one in which islanders only know (as common knowledge) by the end of day n that there are at least n blue-eyed islanders, until n hits 100, at which point all the blue-eyed islanders commit suicide.)
which agree with MK on all sentences of up to k^th knowledge order involving only times up to n. Branching of worlds beyond day n only affects knowledge beyond day n (because, unlike the situation with the surprise paradox, there is no mechanism for knowing anything non-tautological about the future), so this should allow for the existence of an MK world (namely, the “obvious” one in which islanders only know (as common knowledge) by the end of day n that there are at least n blue-eyed islanders, until n hits 100, at which point all the blue-eyed islanders commit suicide.)
With this setup, and initialising at, say, day 0 for simplicity, it seems to me that one can assert that in an MK world, nobody knows their eye colour at day 0 even after the foreigner speaks, and so on day 1 (by the converse of (7)), nobody commits suicide; and so forth.
6 June, 2011 at 2:50 pm
Pace Nielsen
That makes a lot of sense, but I still see a small problem with your statement “With this setup, and initialising at, say, day 0 for simplicity, it seems to me that one can assert that in an MK world, nobody knows their eye colour at day 0 even after the foreigner speaks, and so on day 1 (by the converse of (7)), nobody commits suicide; and so forth.”
One last problem I see arises if we allow an infinite past. For example, let S_t be the statement: knowledge agent K knows at time t that “if nobody commits suicide at time 0 then she has blue eyes”. Suppose that the collection S_t is true for all t in our world MK. Then on day 0 the agent K sees that nobody has committed suicide, and thus knows her eye-color.
Notice that the collection S_t does not run afoul of your latest definition of an MK world, no matter when you choose to initialize your world, because of the memory axiom. (Any initial segment of the S_t implies the rest.)
An easy work-around is either to not have an infinite past, or to require the agents to be blank slates at some point (i.e. to merely know the axioms and all common knowledge).
Thanks for all the clarifications. It seems to me that your most recent formulation of an MK world is a way to put a form of determinism in your system. (One’s knowledge is determined by what came before.)
24 May, 2011 at 10:23 am
Anonymous
Nice post! Dumb questions: 1) Why is it surprising that the “same” problem has different solutions in different epistemic logics, or that a given abstract epistemic logic has nonisomorphic models?; 2)What is a reasonable notion of a morphism between such objects?
24 May, 2011 at 11:25 am
Miracula
In the blue-eyed islander puzzle, if the information is not symmetry, those who having the complete information die. For example, A,B,C are three blue-eyed islanders. The visitor told A that he had told B that he had told C the sentence “there exist some blue-eyed islanders” and that he had told C that he had told B the sentence. But the visitor didn’t told B (C) that he had told A that he had told C (B) the sentence or that he had told C (B) that he had told A the sentence. This case could happen in this way: the visitor met B and C together, and addressed them his speech; and then he met A, and addressed him the same speech plus the fact that he had already addressed B and C. In this case, A died in the third day, B and C survived. What the visitor has said is not important, it’s the way he says really kills people. Always the man who has the complete information is doomed to die.
24 May, 2011 at 11:34 am
Giampiero Campa
Very Interesting. I was also wondering whether perhaps one could represent the internal knowledge of an islander with something like a collection of matrices, in which entries 1,-1,0 indicate the belief that a certain islander has blue, non-blue or unknown-colour eyes. One could then set up initial conditions and some evolution equations (this might be tricky because such evolution equations would probably involve estimating the state of the world before updating the actual knowledge state of an islander) , and let the system evolve to see what happens …
But i am not clear on whether this is feasible at least in theory (not sure if it is possible with a finite data structure), if it would be a good idea (maybe one could prove or disprove convergence theorems or find attraction regions for the system), and what kind of data structure one could use to actually represent knowledge and belief.
24 May, 2011 at 8:10 pm
Fred Lunnon
Section 1, penultimate paragraph:
for
” to determine whether {A_1} has blue eyes or not. ”
read
“to determine whether {I_1} has blue eyes or not.”
Section 2, first bullet:
” which can informally be read as “{K} knows {S} to be true” ”
— or more accurately
” which can informally be read as “{K} believes {S} to be true” ”
Perhaps the distinction is irrelevant for the present application
— as is mentioned later in the section.
Fred Lunnon
[Corrected, thanks = T.]
13 June, 2011 at 12:25 am
Pace Nielsen
I’ve been thinking about this post for the last few weeks, and had some further ideas. I hope than these comments might be helpful. Each of these things is small and kind of obvious (but perhaps useful).
One of the implicit assumptions in the problem is that not only do the islanders see each other’s eyes, but they know that everyone else can see each other’s eyes, and so forth. I would recommend expanding the name of axioms 5 and 6 to make this implicit assumption explicit. This seems to be one of the key pieces that people similarly miss about the visitor’s announcement: sure, the visitor’s announcement didn’t give any new information (where there are two or more blue-eyed islanders), but the fact that you saw that other people saw his announcement (and so forth) *does* give new information.
Also, I realized (and am sure many of you did long ago) that it isn’t necessary to add the atomic propositions about suicide. Instead, one could merely replace axioms 7-9 with the axiom C(K_{i,t}(A_{i}) -> C_{t}(K_{i,t}(A_{i}))). Or, in other words, the new punishment for knowing your eye-color is that you must make it common knowledge that you know your eye-color; and this punishment is common knowledge to everyone. Then, instead of waiting for someone to commit suicide, you just wait to know that they know their eye-color. The benefits of this change are that there are not extra atomic propositions, there is no time delay of a day, and it fits a little more nicely with what I will say next.
Finally, assuming this change, the proof that all MK worlds have all blue-eyed islanders dying on the last possible day reduces to showing that at the k=1 stage, you can induct over time t (starting at some fixed time t_0) and take as your cloud of possible worlds the union of all clouds in all other models which agree up to that time. [The existence of MK worlds also seems to rely on the fact that given the k=0 and k=1 levels of a model are defined and compatible with the given axioms, then the other levels can also be defined compatible with the axioms.]
13 June, 2011 at 12:23 pm
Pace Nielsen
When thinking about that last part, I realized I didn’t really understand what “each M_k projects down to M_{k-1}” means, even when k=2. When k=1 I think this simply means that the first component of M_1 is that given M_0. But when k=2 there is no preferred M_1 model in M_2 (there is only M_0 and clouds of M_1 models).
What am I missing?
The reason I’m having trouble is that I realized the kth order epistemic rule in conjunction with modus ponens allows one to get higher order knowledge to imply lower order knowledge. But, it also seems like lower order knowledge is also defined in terms only on that level of the model. And it wasn’t clear to me how to make those compatible.
So, for example, one of the islanders may be insane (while also extremely logical). Thus, at the M_2 stage he might only consider worlds which never happen (or ignore important worlds that could happen) and I don’t see how these worlds need to be compatible with the M_1 stage.
13 June, 2011 at 1:03 pm
Terence Tao
Because L_1 models projects down to L_0 models, every cloud of L_1 models projects down to a cloud of L_0 models (ignoring repetitions). As a consequence, every L_2 model projects down to an L_1 model. Continuing this procedure recursively, we see that each L_k model projects down to a L_{k-1} model for each k >= 1.
14 June, 2011 at 12:35 pm
Pace Nielsen
I’m not sure I understand.
Let M_0 be an L_0 model.
If I’m understanding correctly, an L_1 model is a collection consisting of a distinguished L_0 model and collections of L_0 models (one for each of the agents) corresponding to (if you will) the cloud of worlds they consider as possible. Let M_1 be such a model.
It was my understanding that M_1 and M_0 are compatible when taking the inverse limit if and only if the distinguished L_0 model in M_1 equals M_0. Is this correct? It was my impression that the clouds of possible worlds have no significance whatsoever in this compatibility. (I see I might be wrong about this as said in my bottom paragraph.)
Now, again if I’m understanding correctly, a model M_2 of L_2 consists of a distinguished L_0 model, and collections of L_1 models (one for each of the agents). I see how any element of any of the collections can map to M_1, I just don’t see how this relates to the formation of the inverse limit.
One way I see around this is that maybe there was a small typo and a model of L_k does not start with a distinguished copy of an L_0 model, but a distinguished copy of an L_{k-1} model. And this is how the inverse system is formed. In that case, I think it would be necessary (to make the higher order epistemic rules consistent with how knowledge is defined) to include in all clouds of possible worlds the actual real world.
On the other hand, by compatibility, maybe you mean that in *each* of the clouds there is a copy of the lower level model. In that case, the real world is picked out in the inverse limit simply by going to the appropriate level. But then, why the need for the distinguished L_0 model?
14 June, 2011 at 1:06 pm
Terence Tao
M_2 consists of an L_0 model M_0, and clouds of L_1 models. We can project each cloud
of L_1 models. We can project each cloud  of L_1 models to a cloud
of L_1 models to a cloud  of L_0 models by replacing each L_1 model with its L_0 projection. The original L_0 model M_0, combined with the projected clouds
of L_0 models by replacing each L_1 model with its L_0 projection. The original L_0 model M_0, combined with the projected clouds  , is then an L_1 model M_1, the projection of M_2.
, is then an L_1 model M_1, the projection of M_2.
For instance: suppose we have three islanders A, B, C. Consider the following nested models of reality:
M_0: A, B, C all have blue eyes.
M_1: A, B, C all have blue eyes, and know that each other have blue eyes, but do not know their own eye colour. In this case, the base L_0 world is M_0, and (say) A’s cloud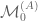 consists of two L_0 worlds: the “true” L_0 world M_0, and also a second L_0 world M_0^{A,-} in which B and C still have blue eyes, but A does not. Similarly for
consists of two L_0 worlds: the “true” L_0 world M_0, and also a second L_0 world M_0^{A,-} in which B and C still have blue eyes, but A does not. Similarly for 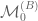 and
and  .
.
M_2: A, B, C have blue eyes, know that each other has blue eyes, and know that the other islanders can see the eye colour of everyone else, but do not know their own eye colour (and know that the other islanders do not know their eye colour either). The base L_0 world is still M_0, and the cloud consists of two L_1 worlds: the “true” L_1 world M_1, and a second L_1 world M_1^{A,-} in which B and C have blue eyes and A does not, and all islanders know each other’s eye colour but not their own. (Thus, for instance, B’s L_0 cloud
consists of two L_1 worlds: the “true” L_1 world M_1, and a second L_1 world M_1^{A,-} in which B and C have blue eyes and A does not, and all islanders know each other’s eye colour but not their own. (Thus, for instance, B’s L_0 cloud  of M_1^{A,-} consists of two L_0 worlds, one in which only C has blue eyes, and one in which both B and C have blue eyes.)
of M_1^{A,-} consists of two L_0 worlds, one in which only C has blue eyes, and one in which both B and C have blue eyes.)
To project M_2 onto M_1, we project each L_1 cloud such as to an L_0 cloud
to an L_0 cloud 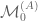 by taking each of the L_1 worlds in the former cloud (in this case, M_1 and M_1^{A,-} and replacing them with their L_0 projections (in this case, M_0 and M_0^{A,-}). In some cases this may reduce the cardinality of the cloud, although this is not the case in this particular running example. (For instance, one could consider a variant M’_2 of M_2 in which each islander allows the possibility that the other islanders somehow know their own eye colour, in which case one has to add some more L_1 worlds to
by taking each of the L_1 worlds in the former cloud (in this case, M_1 and M_1^{A,-} and replacing them with their L_0 projections (in this case, M_0 and M_0^{A,-}). In some cases this may reduce the cardinality of the cloud, although this is not the case in this particular running example. (For instance, one could consider a variant M’_2 of M_2 in which each islander allows the possibility that the other islanders somehow know their own eye colour, in which case one has to add some more L_1 worlds to  to reflect these possibilities, but the projections to the L_0 clouds remain unchanged.)
to reflect these possibilities, but the projections to the L_0 clouds remain unchanged.)
15 June, 2011 at 11:31 am
Pace Nielsen
Thank you for taking the time to spell this out so completely. I think I understand now. The way I’m picturing what you said is that, thinking of these models as nested sets of nested sets, etc…, we remove the “deepest level” of the nesting. We keep all of the “distinguished” L_0 models (at any depth) and throw away the last layer of clouds. Or, in other words, to build up to the next level, we throw on possible worlds at the bottom level.
I think I also now see how to get around my issues with the higher epistemic rules. Let me describe what I was thinking and how it fits now. For simplicity, let us consider the case with only two agents A and B. Let P,Q,R,S be the four worlds corresponding to the four cases (respectively) A and B have blue eyes, A is brown-eyed and B is blue-eyed, A is blue-eyed and B is brown-eyed, and finally A and B both have brown eyes.
We start with the model M_0=P. So, the “real world” consists of both A and B having blue eyes.
Now, let M_1={P, {Q},{R}}. This model projects to M_0. We can interpret this world as the one where A believes that he has brown eyes but also believes that B has blue eyes; whereas B thinks he has brown eyes but A has blue eyes. Note in particular that neither A nor B know that their eye color is blue.
Now let M_2={P,{Q,{P},{P}},{R,{P},{P}}}. This model projects to M_1. We can interpret this world as the one where A only considers the world Q (where he has brown eyes and B has blue eyes) but in that world, he only considers the case where he believes that he will believe he has blue eyes (and he also believes that B will believe they both have blue eyes).
Let K be the predicate “A knows” and let I be the statement “A has blue eyes”. In our model, we have K(K(I)). We also have \neg K(I). My issue was that the way I was interpreting what you were saying I thought that K(K(I)–>I) was true. But it isn’t. The statement K(I)–>I is not true in the L_1 model {Q,{P},{P}}, even though K(I) is true in that model and I is true in all of the possible worlds of that model and also in the “truly real world”. The problem is that I is not true in what that models thinks of as the real world (namely, Q).
Again, thank you for clarifying this for me.
7 October, 2011 at 9:34 am
del
Interesting post! Another approach is to use “dynamic” epistemic logics, which are designed for reasoning about the kind of multi-agent information change going on in this puzzle. The simplest of these systems, Public Announcement Logic, has been used to model similar puzzles. For example, see the following:
Click to access oucs-2004-10.pdf
Click to access LonelyNumber.pdf
Click to access PP-2005-06.text.pdf
11 May, 2012 at 9:41 pm
Голубоглазые островитяне | Блог Хеллера
[…] Опять же по наводке Даниила подробное решение задачи опять же Терренсом Тао. В частности интересен […]
6 August, 2013 at 8:00 am
Pace Nielsen
I’ve been thinking about the blue-eyed islander puzzle, and related conundrums, on and off over the past year. I have a thought which may be of interest to those who followed this blog post last year. It relates to Löb’s theorem: http://en.wikipedia.org/wiki/L%C3%B6b%27s_theorem In particular, I’m interested in whether it is possible to formalize the fact that it is common knowledge that all of the islanders are perfectly logical, while also retaining the standard solution in a complex enough system (say, encompassing first order arithmetic, to allow for diagonalization arguments).
So, here is my framework. Suppose you are one of the islanders, and you know/believe that all of the other islanders are perfectly logical. Let’s do as above, and view knowledge/belief as a predicate obeying certain rules. One axiom is the “rule of necessitation” which states that if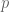 is a valid statement (i.e. provable from the axioms), then
is a valid statement (i.e. provable from the axioms), then  is also a valid statement. In other words, these islanders at the very least know what is provable.
is also a valid statement. In other words, these islanders at the very least know what is provable.
Now, is this rule of necessitation, itself, common knowledge? As usually stated, the puzzle seems to point to a yes (else, what would it mean to believe the others are perfectly logical?).
So, let me ask you: if after the first day nobody has committed suicide what can you conclude? It appears that we would then know that there are no contradictions. Why? If the logical system *is* inconsistent then your fellow islanders would have found an inconsistency. They then would have killed themselves, for by the principle of ex falso quodlibet they then believe they know their eyecolor. Of course, if we now know that the system is consistent, and since the system is complicated enough to allow for Gödel numbering, this leads to a contradiction, forcing us to kill ourselves on the second day.
On the other hand, if we cannot conclude from the lack of suicides that the system is consistent, then why should we be able to conclude that the others do not know their eye color? If it is possible that they just missed some inconsistency, isn’t it just as likely that they missed something that would allow them to derive their eye color? (Indeed, if there is an inconsistency, that would be just the thing to convince them that they know their own eye color!)
4 June, 2016 at 5:02 pm
It ought to be common knowledge that Donald Trump is not fit for the presidency of the United States of America | What's new
[…] of the distinction comes from the blue-eyed islander puzzle, discussed previously here, here and here on the blog. (By the way, I would ask that any commentary about that puzzle be directed to those […]
11 November, 2016 at 3:02 pm
Cosmia Nebula in Iceland
Concerning “formalise the other assumptions of the puzzle:”
I think there needs to be one more set of assumptions, that is, “Anyone who does not learn their own eye colour is blue, must not commit suicide the next day”
\displaystyle C( \neg K_{i,t}(A_i) \implies \neg S_{i,t+1} ). \ \ \ \ \ (7)
21 January, 2017 at 10:28 pm
nmks
Blue-eyed islanders puzzle. I have not read through all of the hundreds of posts on this site, but I’ve read about this puzzle on various websites.
Most suggest that the debate is about which of two possible solutions is correct. 1. that the visitor to the island imparts no new information and thus nothing happens, and 2. that the visitor’s announcement starts the induction process. My question is: why not a third solution, namely that the induction process DOES take place, but the visitor’s announcement is not needed for that to happen.
Since there are many versions of this puzzle I will use the one where, instead of committing ritual suicide, the islanders can leave the island. Everything else is the same. (The only reason i want to use this version is because the reasoning I am going to give is easier to phrase in this situation, because in this case the result is something the islanders all want.)
So, let’s say the islanders all WANT to leave the island, but when they were put on the island, they were told they can only leave if and when they know their own eye color. And there’s a boat that arrives and leaves every day at mid-day, in case any of them should find themselves in that happy situation.
Since there are 100 blue-eyed people, everyone knows that everyone else knows that there are many blue-eyed people there. (I know it won’t work for 3 or fewer of any color). Now, is it really necessary to have someone say out loud “I see someone with blue eyes”? Why wouldn’t the islanders, all being logical and knowing that everyone else is logical, simply ASSUME that blue eyes on the island is common knowledge, and also assume that everyone else will assume that because they too are logical. So, rather than waiting for some visitor who may or may not ever say that statement out loud, why would they not simply ACT AS IF that statement had been spoken?
I mean, whom would that statement benefit anyway? The hypothetical solitary blue-eyed person who, without the statement, could not leave? But hypothetical people can’t hear anyway. So it’s only for the benefit of the calculation. So why wouldn’t all these logical islanders, all of whom want to get off the island, get around that by ASSUMING the common knowledge, and start counting the days, via the induction process, from the moment they are all deposited on the island and told that they can only leave if/when they know their eye-color? Sure, in their mental calculation they can start with the case of just 1 islander, but say “In that case I will assume that someone has made it common knowledge that there is at least one blue-eyed person, and that hypothetical solitary blue-eyed person would then know it was him/her since he/she doesn’t see anyone else with blue eyes.” And they can confidently know that every other islander will be making the same assumption because they all know that everyone is perfectly logical. I mean, would they really sit around for years thinking “oh I do wish that the boat operator who comes here everyday would just announce that there is at least one blue-eyed person here, and then we can all start getting off this island!”?
(I don’t know if my reasoning is correct or not. I am not a mathematician, so I can’t read the formulas and symbols I sometimes see with the various explanations. I just want to where my reasoning is flawed, if it is. I’m also wondering if anyone has tested this problem in practice? e.g., by having a bunch of people in a room, putting colored stickers on their forehead and having opportunities to leave the room at regular intervals, such as every minute. (Or, maybe more people would be willing to play if, instead of leaving the room, make it so they can start eating when they’ve worked out the color. But they would all have to be very logical.) Thanks for reading!
21 January, 2017 at 10:39 pm
Cosmia Nebula in Iceland
“blue eyes on the island is common knowledge” cannot be assumed, because it is not public knowledge before the announcement.
Consider the simple case of 2 people with blue eyes. Both know “there are blue eyes on this island”, but both do not know “everyone knows that ‘there are blue eyes on this island'”.
Then in the case of 3 people with blue eyes. All know “everyone knows that ‘there are blue eyes on this island'”, but something more subtle happens:
1 knows that 2 and 3 has blue eyes, but 1 does not know that 1 has blue eyes. Thus 1 must consider the possible world where only 2 and 3 has blue eyes. In that world, 2 would not know that “3 knows that ‘there are blue eyes on this island'”.
Thus, 1 does not know that “2 knows that “3 knows that “there are blue eyes on this island”””, even though 2 knows that “3 knows that “there are blue eyes on this island””.
After the public announcement, everyone knows that everyone knows that everyone knows that there are blue eyes on this island, and in particular, 1 knows that “2 knows that “3 knows that “there are blue eyes on this island”””, thus this public announcement gave them new information.
Now, if you think hard about the 3 blue eyes case, you can generalize to the general case.
21 January, 2017 at 11:19 pm
nmks
Thank you for your reply! I have thought it out for the case of 1 blue-eyed person, two blue-eyed people, three blue-eyed people, and more, and I understand the reasoning. I’ve drawn numerous charts over the last few months, and can see that one will always get down to that situation where there is one blue-eyed person who will not know until the public announcement. But I took all of that into account and suggested that I nevertheless think there may be a another solution. I am wondering where specifically my reasoning goes wrong, if it does. (Which is a bit different from asking for the correct solution. And I know my post was very long, and I apologize for that, but it had to be in order to explain what I mean. Because it surprises me that I have not read my argument in any of the posts (but, as I stated at the start, I have not read everything on this thread, although I have read much about this puzzle.) Thanks again for replying!
22 January, 2017 at 12:08 am
Cosmia Nebula in Iceland
It would benefit to think about the symmetry of the situation. Suppose they suddenly decide to “count the days”, how would they decide at the same time without communication? The only communication, remember, is the act of leaving the island.
So they can’t decide to count the days at the same day without something to “synchronize” them, such as the public annoucement.
They cannot assume that blue eyes on the island is common knowledge, because it is not common knowledge, which I explained why in my last comment.
They would sit around for years thinking “oh I do wish that the boat operator who comes here everyday would just announce that there is at least one blue-eyed person here, and then we can all start getting off this island!”, because that would give them new information.
Imagine the island has exactly 2 people, person 1 has red eyes, person 2 has blue eyes.
Suppose person 1 gets tired of waiting and decides to pretend there had been a public announcement “there is at least one blue eye” in the afternoon of day 1.
Then at the noon of day 2, he sees that person 2 hasn’t left, and would think that this logically proves that he has blue eyes.
Then at the noon of day 3 he went to the boat operator and says he has blue eyes, and of course gets it wrong.
Person 1 goes back and gets so angry that he becomes able to speak, so he asks why hasn’t person 2 left. Person 2 replies with surprise, since he has always thought that both of them probably has red eyes.
22 January, 2017 at 8:12 am
nmks
Thanks. That’s interesting, and I will have to think about it a lot more.
The examples with 1, 2, or even 3 people clearly don’t work without the announcement. But the original puzzle says there are 100 blue-eyed people.
I thought that the people WILL have a synchronization point at which to start calculating, and it would be the moment when, as they are deposited on the island, they are told by the boat operator: “here you stay, until you work out your eye-color. If you ever do”. That would be Day 1.
However, I don’t know if that changes the initial premise of the puzzle and if THAT announcement has a similar effect to that of the visitor in the Terry Tao version. It would be interesting to see if this apparently slight change to the initial puzzle does, in fact, lead to a different result. And I’ll have to do a lot more thinking about it all before I reject my reasoning, which I will happily reject if/when I see it to be incorrect.
What I really need to do is get about 30 logicians at a dinner party, put stickers on their foreheads, and say they can’t start eating until they know their sticker color, with opportunities for them to announce their color every minute or so. Trouble is, I don’t know many logicians and most of my friends tend to run the other way whenever I start to mention this puzzle… :)
22 January, 2017 at 9:11 am
nmks
I should add that in the dinner party experiment, in order to ensure synchronization, they should all be given a few minutes to just look around at every one else, after which the person conducting the experiment can say, “okay, opportunities to announce you sticker color will be when the timer rings, which it will every minute, beginning NOW.”
22 January, 2017 at 2:45 pm
Cosmia Nebula in Iceland
If you want that experiment, 3 people is good enough. If you want a big experiment, you’d have to use the Internet.
Besides, imagine 3 people, 1 blue, 1 green, 1 red. The announcer came and said, “beginning NOW”.
How are they going to decide which color to synchronize to??
22 January, 2017 at 2:55 pm
Anonymous
I agree that in that situation it would definitely not work. I will continue to fine-tune my thinking about this, using the situation where, like in the original puzzle, there are only blues and many browns, and many of them, so everyone can see lots of just 2 colors and may think that he/she is the only one with a third color if there were a third color, which of course they don’t know. Will probably post something in a few days after I’ve had a chance to rethink… (But SO GLAD that someone’s willing to discuss this with me!!!!!! Thank you!)
22 January, 2017 at 2:57 pm
Anonymous
No idea why that last post listed me as Anonymous. Still new to this…
30 July, 2017 at 1:15 am
lensgravatar
Argument by induction works on a mathematical model where you have proved the statement true for 1 and know that if it is true for n then it is true for n+1. Also, it is well known that if you assume a premise to be true that is actually false, then you can prove pretty much anything you want. A lot of paradoxes play off this notion by having a loosely defined situation. So, for example, if you start with “If 1=2 then…” you are toast. In this puzzle if there are more than 3 blue eyed people, then everyone knows there are more than 1 blue eyed person. So you cannot start a valid argument by induction by saying “If there was one blue eyed person…”, because it is a false premise. So the paradox arises by conflating logic with a situation. Interesting to watch Tao dig ever deeper holes for himself on this one.
30 July, 2017 at 4:55 am
nmks
Thanks, lensgravatar, you may have unraveled the mystery!
But first, there seem to be 2 similar threads, one called The Blue eyed islanders, the other called Epistemic logic. I originally posted on the latter, but recently have been posting on the former, so I don’t know if you have read what I wrote there.
I too was skeptical about including the n =1, n = 2, or n =3 scenarios in a situation where everyone can see at least 99 blue-eyed people.
So here is a re-post of what I put on the other thread a few days ago. I wonder if you would agree with it. (note that I wrote it before I read your response because it was on a different thread)
The induction process sounds logical. And yet.. I wonder if one can really base everything on a hypothetical situation where there is just one blue eyed person when everyone knows there are at least 99 of them..Because that’s what is happening in all the nested scenarios – one always ends up with that hypothetical situation where there is just one blue-eyed islander, and because he/she has not heard the announcement nothing can happen. (But – hypotheical people cannot hear anyway!!!)
Since it is easier (at least for me) to imagine scenarios where the outcome is something the islanders want (like being able to leave the island) rather than something they would wish to avoid (like ritual suicide) I will go back to the scenario I proposed a few posts earlier – where instead of ritual suicide the goal is to get off the island, and when the people were put on the island they were told (all at once) that they can leave only if/when they know their eye color. And a boat comes and goes every day to give them the chance to leave if they can.
Since they are all logical people and know that everyone else is logical too, would they really sit around for years thinking “oh I do wish that the boat operator who comes here every day would just hurry up and announce that there is at least one blue-eyed person here (which we all already know anyway) so we can start getting off this island!”?
Why not just ASSUME (i.e., ACT AS IF) the boat operator had made the announcement. Being logical they would know that everyone would think so too. (They could still start with the one person scenario for the purpose of calculating WHEN they can leave, but those calculations can begin as soon as they are told the rules about leaving. THAT would then be the clock starter, and not the announcement about eye color, since the color they could work out as long as they make the assumption mentioned above.)
If someone could explain to me if this is correct or, if not, where the fault is in this argument, that would be great.
(I will be away from the internet for a few days so will not be able to respond to any comments during that time)
18 October, 2018 at 4:58 am
Anonymous Coward
I could have sworn I had read this one, yet it took me quite some searching to find it … Sir Terence, if you don’t mind tagging the blue-eyed islanders posts so they can be all be found from one another? See here:
https://terrytao.wordpress.com/tag/blue-eyed-islanders/
https://terrytao.wordpress.com/tag/blue-eyed-islander-puzzle/
You have used two distinct tags :-/
Apart from that, I am grateful for this post. While I could accept the induction argument for what I could see it did prove, I could not by any means accept it as a proof that they had to last as long as ’til the nth day.
And I see that the Wikipedia article on common knowledge still posts the induction “proof” without any reservation that it is an upper bound.
[Tag changed – T.]
18 October, 2018 at 8:37 pm
Think
People talk about simulating reality. How does one go about simulating this without feeding in the rule of deliberate suicide apriori? Everything is deterministic in effect. However the way the puzzle is formulated seems to introduce some sort of free will.
21 October, 2018 at 5:10 pm
Alexandru Soare
A suggestion that may at first seem outside of this subject and the like, but with some thought may be realized to be relevant:
The Shape of Goodness
1. All things want to be that which they truly are and no thing else; often they do not know what they truly are, and this is unhappiness, pain.
2. An evil thing is, what it truly is, is something that prevents or seeks to prevent other things from being what they truly are (or confuse the subject); and an evil thing would wish to be no thing else.
3. We have two categories, one of all that is not evil (good), and the other being evil. Goodness can speak for all that is not evil (good) and says that the difference between the two is in fact not only the previous categorical difference, but also very much greater, the greatest difference possible, always more, entirely spiritual beyond measure, and goodness says this because it is more good for this to be thus.
4. Good and evil are not opposites; they are very different, no reflection down any axis. The opposite of a good thing in every way is another good thing, and the opposite of an evil thing in every way is another evil thing.
5. Goodness is the only categorical thing the opposite of which is entirely contained within itself. The shape of goodness is a box whose opposite is fully within it; that is, a protrusion of it is the opposite of the entire ensemble of box and protrusion, and it can easily be computed, and seen to be a Klein-bottle like shape. Systems which fit within such boxes are likely good, functional.
9 February, 2020 at 11:08 pm
Anonymous
Dear Pro. Tao,
I was really puzzled about the blue-eyes island problem for the first time I saw it, However, I finally found the argument 2 just an inconspicuously wrong use of reduction to absurdity (though it is more like induction!). The reason is as follow:
1. If we regard argument 2 as induction, it means that for every n=1,2…100, there is a foreigner saying “blue-eyed people exist”. In fact, foreigner only said it for n=100, so argument 2 is not induction.
2. We can change argument 2 to other word which is more like reduction to absurdity: people-1 assumes himself brown eyes, then he wants to deduce that other 99 blue-eyed people will die on the 99th day. The specific deduction of people-1 is the reduction to absurdity of people-2 who assumes himself brown eyes, then wants to deduce that other 98 blue-eyed people will die on the 98th day. Reduction to absurdity is go on like this until people-100.
3. Unfortunately, this reduction to absurdity is totally wrong for which it violates a basic rule—–if the assumption may change other certain precondition (especially when we even don’ t know it is true or false!), then the precondition should only be used to compare finally, rather than be still used to deduce as correct precondition (after assuming, the precondition may be wrong). In the blue-eyes island problem, once a people assuming himself brown eyes, the information of “blue-eyed people exist” may change (actually change at people-98), then the deduction base on “blue-eyed people exist” is no longer reliable (because the assumption may be wrong).
I believe from begin to end: no new information, and no new result!
9 February, 2020 at 11:28 pm
Anonymous
supplement for 3: After people-1 assuming himself brown eyes, the assumption of people-2 is actually people-1 and people-2 are both brown eyes (because he just think about the rest 98 people). On his view, people-1 is blue-eyed, his assumption is wrong, so the precondition “blue-eyed people exist” should be revalued!
10 February, 2020 at 12:13 am
.
There is a pretty clean information theoretic argument for this in the number on forehead model in communication complexity. I am surprised that this result is not thought to be that unsurprising. Please look up NOF model.
26 November, 2021 at 7:59 am
Brad Fortner
After giving this problem some more thought, I would like to retract any previous comments I may have posted. The formal notation of logic is interesting, but in my opinion, it describes the problem without solving it. The following is my best attempt at a solution, containing several conditional solutions, and only employing basic reasoning, and leaving the symbolic logic for others to use.
This problem, along with its many variants and similar problems, reminds me of Schelling Points, and in fact, they may be examples of that concept. A Schelling Point exists among logical minds, whenever there is no explicit information, and yet there is an option, recognized by some players, that naturally stands out from the other options. Accepting a Schelling Point as the best option, and acting on that option, implies that the players who do so are motivated to err on the side of action. This relates to the Blue-Eyed Islanders Problem, in that its solution depends on several conditions, the motivation of the islanders to act being one of those conditions.
The fact that the islanders existed, still on the island, at the time of the visit by the outsider means one of two things. Either they were in the process of counting the days until they would take action, or they were not in that process, due to uncertainty. In the first case, the visitor’s announcement would not give new information, and they would continue the countdown (the Islanders Problem is solved for that condition). In the second case, the announcement would have to give certainty in the knowledge everyone needed to start a countdown. They could have started a countdown earlier, but uncertainty prevented it. Perhaps they were lacking the knowledge that everyone was a pefect logician. Or maybe they were unsure that everyone knew their day of arrival. Or perhaps they arrived on different days, and not all of the arrival dates were known to be known by everyone. The announcement by the visitor would have to clear up any and all uncertainty, and it must effectively reset the starting date for any possible countdown. The previous time must be ignored, since it held uncertainty, and a new era must begin, with no uncertainty.
Does the visitor’s announcement achieve these two requirements – 1. Give certainty in perfect knowledge by everyone, about everyone (other than their own eye color). 2. Give the logical starting point for a countdown. It seems that if (1) is met, then (2) is also achieved, and the logical start for a countdown is the day that (1) is achieved. So… is (1) achieved by the visitor’s announcement? If so, then we have another conditional solution to the Islanders Problem. That is, if we assume that some islanders are unsure about the knowledge of all of the islanders, then (1) is not achieved, because the visitor does not address the islanders’ capacity for using logic, or the uniformity of this trait over all islanders. The visitor says nothing that clears up uncertainty that some islanders may have about other islanders. The islanders will not begin a countdown, and will not take action at this time. Alternatively, if we assume that the only uncertainty among the islanders is the date of everyone having the required information (the starting point), then (1) is already met, and the visitor’s announcement must be enough to achieve (2) on its own, in order to begin the countdown. It seems that the visitor’s announcement about eye color is a landmark on the collective psyche of the islanders, and is the only thing needed to begin a countdown by people who are certain about their shared knowledge, and are clearly motivated to take action at the first opportunity. Whether the Problem involves escaping from the island by boat, or leaving this space-time realm by death, the islanders are very motivated to act on their knowledge. Under this last condition, they will err on the side of action.
Brad Fortner – 11/26/2021