If is a locally integrable function, we define the Hardy-Littlewood maximal function
by the formula
where is the ball of radius
centred at
, and
denotes the measure of a set
. The Hardy-Littlewood maximal inequality asserts that
for all , all
, and some constant
depending only on
. By a standard density argument, this implies in particular that we have the Lebesgue differentiation theorem
for all and almost every
. See for instance my lecture notes on this topic.
By combining the Hardy-Littlewood maximal inequality with the Marcinkiewicz interpolation theorem (and the trivial inequality ) we see that
for all and
, and some constant
depending on
and
.
The exact dependence of on
and
is still not completely understood. The standard Vitali-type covering argument used to establish (1) has an exponential dependence on dimension, giving a constant of the form
for some absolute constant
. Inserting this into the Marcinkiewicz theorem, one obtains a constant
of the form
for some
(and taking
bounded away from infinity, for simplicity). The dependence on
is about right, but the dependence on
should not be exponential.
In 1982, Stein gave an elegant argument (with full details appearing in a subsequent paper of Stein and Strömberg), based on the Calderón-Zygmund method of rotations, to eliminate the dependence of :
The argument is based on an earlier bound of Stein from 1976 on the spherical maximal function
where are the spherical averaging operators
and is normalised surface measure on the sphere
. Because this is an uncountable supremum, and the averaging operators
do not have good continuity properties in
, it is not a priori obvious that
is even a measurable function for, say, locally integrable
; but we can avoid this technical issue, at least initially, by restricting attention to continuous functions
. The Stein maximal theorem for the spherical maximal function then asserts that if
and
, then we have
for all (continuous) . We will sketch a proof of this theorem below the fold. (Among other things, one can use this bound to show the pointwise convergence
of the spherical averages for any
when
and
, although we will not focus on this application here.)
The condition can be seen to be necessary as follows. Take
to be any fixed bump function. A brief calculation then shows that
decays like
as
, and hence
does not lie in
unless
. By taking
to be a rescaled bump function supported on a small ball, one can show that the condition
is necessary even if we replace
with a compact region (and similarly restrict the radius parameter
to be bounded). The condition
however is not quite necessary; the result is also true when
, but this turned out to be a more difficult result, obtained first by Bourgain, with a simplified proof (based on the local smoothing properties of the wave equation) later given by Muckenhaupt-Seeger-Sogge.
The Hardy-Littlewood maximal operator , which involves averaging over balls, is clearly related to the spherical maximal operator, which averages over spheres. Indeed, by using polar co-ordinates, one easily verifies the pointwise inequality
for any (continuous) , which intuitively reflects the fact that one can think of a ball as an average of spheres. Thus, we see that the spherical maximal inequality (3) implies the Hardy-Littlewood maximal inequality (2) with the same constant
. (This implication is initially only valid for continuous functions, but one can then extend the inequality (2) to the rest of
by a standard limiting argument.)
At first glance, this observation does not immediately establish Theorem 1 for two reasons. Firstly, Stein’s spherical maximal theorem is restricted to the case when and
; and secondly, the constant
in that theorem still depends on dimension
. The first objection can be easily disposed of, for if
, then the hypotheses
and
will automatically be satisfied for
sufficiently large (depending on
); note that the case when
is bounded (with a bound depending on
) is already handled by the classical maximal inequality (2).
We still have to deal with the second objection, namely that constant in (3) depends on
. However, here we can use the method of rotations to show that the constants
can be taken to be non-increasing (and hence bounded) in
. The idea is to view high-dimensional spheres as an average of rotated low-dimensional spheres. We illustrate this with a demonstration that
, in the sense that any bound of the form
for the -dimensional spherical maximal function, implies the same bound
for the -dimensional spherical maximal function, with exactly the same constant
. For any direction
, consider the averaging operators
for any continuous , where
where is some orthogonal transformation mapping the sphere
to the sphere
; the exact choice of orthogonal transformation
is irrelevant due to the rotation-invariance of surface measure
on the sphere
. A simple application of Fubini’s theorem (after first rotating
to be, say, the standard unit vector
) using (4) then shows that
uniformly in . On the other hand, by viewing the
-dimensional sphere
as an average of the spheres
, we have the identity
indeed, one can deduce this from the uniqueness of Haar measure by noting that both the left-hand side and right-hand side are invariant means of on the sphere
. This implies that
and thus by Minkowski’s inequality for integrals, we may deduce (5) from (6).
Remark 1 Unfortunately, the method of rotations does not work to show that the constant
for the weak
inequality (1) is independent of dimension, as the weak
quasinorm
is not a genuine norm and does not obey the Minkowski inequality for integrals. Indeed, the question of whether
in (1) can be taken to be independent of dimension remains open. The best known positive result is due to Stein and Strömberg, who showed that one can take
for some absolute constant
, by comparing the Hardy-Littlewood maximal function with the heat kernel maximal function
The abstract semigroup maximal inequality of Dunford and Schwartz (discussed for instance in these lecture notes of mine) shows that the heat kernel maximal function is of weak-type
with a constant of
, and this can be used, together with a comparison argument, to give the Stein-Strömberg bound. In the converse direction, it is a recent result of Aldaz that if one replaces the balls
with cubes, then the weak
constant
must go to infinity as
.
— 1. Proof of spherical maximal inequality —
We now sketch the proof of Stein’s spherical maximal inequality (3) for ,
, and
continuous. To motivate the argument, let us first establish the simpler estimate
where is the spherical maximal function restricted to unit scales:
For the rest of these notes, we suppress the dependence of constants on and
, using
as short-hand for
.
It will of course suffice to establish the estimate
for all continuous , as the original claim follows by replacing
with
. Also, since the bound is trivially true for
, and we crucially have
in three and higher dimensions, we can restrict attention to the regime
.
We establish this bound using a Littlewood-Paley decomposition
where ranges over dyadic numbers
,
, and
is a smooth Fourier projection to frequencies
; a bit more formally, we have
where is a bump function supported on the annulus
such that
for all non-zero
. Actually, for the purposes of proving (7), it is more convenient to use the decomposition
where is the projection to frequencies
. By the triangle inequality, it then suffices to show the bounds
for all and some
depending only on
.
To prove the low-frequency bound (8), observe that is a convolution operator with a Schwartz function, and from this and the radius restriction
we see that
is a convolution operator with a Schwartz function of uniformly bounded norms. From this we obtain the pointwise bound
and the claim (8) follows from (2).
Now we turn to the more interesting high-frequency bound (9). Here, is a convolution operator with an approximation to the identity at scale
, and so
is a convolution operator with a function of magnitude
concentrated on an annulus of thickness
around the sphere of radius
. This can be used to give the pointwise bound
which by (2) gives the bound
for any . This is not directly strong enough to prove (9), due to the “loss of one derivative” as manifested by the factor
. On the other hand, this bound (12) holds for all
, and not just in the range
.
To counterbalance this loss of one derivative, we turn to estimates. A standard stationary phase computation (or Bessel function computation) shows that
is a Fourier multiplier whose symbol decays like
. As such, Plancherel’s theorem yields the
bound
uniformly in . But we still have to take the supremum over
. This is an uncountable supremum, so one cannot just apply a union bound argument. However, from the uncertainty principle, we expect
to be “blurred out” at spatial scale
, which suggests that the averages
do not vary much when
is restricted to an interval of size
. Heuristically, this then suggests that
Estimating the discrete supremum on the right-hand side somewhat crudely by the square-function,
and taking norms, one is then led to the heuristic prediction that
One can make this heuristic precise using the one-dimensional Sobolev embedding inequality adapted to scale , namely that
To prove this inequality, one starts with the local one-dimensional Sobolev inequality
rescales this inequality to the scale , and then covers the interval
by boundedly overlapping intervals of length
.
A routine computation shows that
(which formalises the heuristic that is roughly constant at
-scales
), and this soon leads to a rigorous proof of (13).
An interpolation between (12) and (13) (for sufficiently close to
) then gives (9) for some
(here we crucially use that
and
).
Now we control the full maximal function . It suffices to show that
where ranges over dyadic numbers.
For any fixed , the natural spatial scale is
, and the natural frequency scale is thus
. We therefore split
and aim to establish the bounds
for each and some
depending only on
and
, similarly to before.
A rescaled version of the derivation of (10) gives
for all , which already lets us deduce (14). As for (15), a rescaling of (11) gives
for all . Meanwhile, at the
level, we have
and
and so
which implies by rescaled Sobolev embedding that
In fact, by writing , where
is a slight widening of
, we have
square summing this (and bounding a supremum by a square function) and using Plancherel we obtain
Interpolating this against (16) as before we obtain (15) as required.

47 comments
Comments feed for this article
21 May, 2011 at 6:25 pm
Yao
Dear Professor Tao, I want to ask you a question that may be ridiculous, I often see many books about harmonic analysis, what does the word “harmonic ” mean? When we call a subject complex analysis or real analysis, may be the most important character of the subject is related to real function or complex function. But when it comes to harmonic analysis, I am not sure why we call this subject harmonic analysis. Does it originated from researching harmonic function ? Thank you.
22 May, 2011 at 9:10 am
Terence Tao
http://en.wikipedia.org/wiki/Harmonic
22 May, 2011 at 12:25 pm
iosevich
Hi Terry,
A very nice entry on one of my favorite topics, the spherical averaging operator!
A quick remark about a connection between your entry and one of your earlier entries on incidence theorems in higher dimensions. One can use the proof of Stein’s result, and also Bourgain/Mockenhaupt, Seeger and Sogge to prove an incidence theorem for spheres of arbitrary radius and homogeneous point sets. This was done in my paper with Hadi Jorati and Izabella Laba that I mentioned in relation to your incidence paper with Jozsef.
22 May, 2011 at 10:28 pm
John Snow
I believe my brain did indeed just implode. Thank you for that. ;)
23 May, 2011 at 12:32 am
xifeiautao
Hi terence,
The notions of Fourier analysis and harmonic analysis always confused me. In many books they have the same contents. For example, Loukas’s book, Fourier analysis, has similar contents with harmonic analysis written by Stein. So how to make a distinction between Fourier analysis and harmonic in mordern analysis?
23 May, 2011 at 9:02 am
Terence Tao
There is no fixed definition of any given mathematical field, but Fourier analysis and harmonic analysis do indeed generally refer to overlapping areas of mathematics. Note that harmonic analysis is usually divided into abstract harmonic analysis (over general classes of groups, such as locally compact abelian groups), real-variable harmonic analysis (usually over Euclidean spaces or manifolds), and applied harmonic analysis (e.g. use of wavelets in real-world applications).
Real-variable harmonic analysis certainly contains Fourier-analytic objects, such as Fourier multipliers, within its purview, but it also studies other objects, such as maximal operators, which do not have any direct connection to the Fourier transform, and in particular can deploy combinatorial or geometric methods (e.g. covering lemmas) that would usually not be termed Fourier analysis. Real-variable harmonic analysis also tends to focus attention on bounding various linear, sublinear, or multilinear operators in spaces such as L^p spaces, whereas Fourier analysis has traditionally been concerned with questions such as convergence or uniqueness of Fourier series. (Of course, the two types of questions are related to each other in many ways.)
The term Fourier analysis can also be reasonably applied to other applications of the Fourier transform that are not traditionally considered harmonic analysis, such as in additive combinatorics, or additive number theory.
Ultimately, though, these terms are not rigorously and statically defined, but evolve with the development of the field (and different schools of mathematicians may use these terms in slightly different ways). Much as mathematics can be defined as what mathematicians do, perhaps the most robust definition of “Fourier analysis” and “harmonic analysis” is “what Fourier analysts do” and “what harmonic analysts do”.
23 May, 2011 at 7:56 am
Anonymous
Dear Prof. Tao,
it seems that one or more of the links to your lecture notes at the beginning of the post are broken – they lead back to the post itself.
[Corrected, thanks – T.]
23 May, 2011 at 9:29 pm
Análisis y aplicaciones: conferencia en honor de Elias M. Stein | Series divergentes
[…] Recientemente, en conmeración de esta conferencia, Terence Tao publicó en su blog una serie de artículos sobre algunos de los resultados de Stein más importantes, entre los que se encuentran el teorema de interpolación, el principio maximal y el teorema maximal esférico. […]
24 May, 2011 at 4:17 pm
Sixth Linkfest
[…] Tao: Stein’s maximal principle, Stein’s spherical maximal theorem, Locally compact topological vector […]
10 July, 2011 at 11:34 am
K
Dear Dr. Tao,
I’m not familiar with the union bound argument that mention. What is the argument you would like to make? Do you need a finiteness assumption (on the radii) for it, or could you have a countable supremum?
K
10 July, 2011 at 4:11 pm
Terence Tao
The union bound, in this context, asserts that
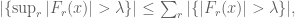
or in its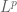 version,
version,
It is only usable in the case when r is finite or countable.
10 July, 2011 at 6:20 pm
K
Got it. Thanks!
K
11 July, 2011 at 12:06 am
newsboy
wonderful!
29 April, 2012 at 4:22 pm
Bài 1: Hàm cực đại Hardy-Littlewood | Quán cóc Toán
[…] để chỉ ra không phụ thuộc vào số chiều của không gian. Chi tiết xem bài viết trên blog của Terence Tao. Trong chuỗi bài giảng này, tôi sẽ (cố gắng) trở lại vấn đề về ước […]
20 September, 2012 at 6:16 am
Hahn
Hello Terrence Tao,
Can you explain a little bit more detail about the “blurred out” technique that you used to estimate:
This is a crucial thing to understand your post thoroughly.
Thank you,
Hahn.
20 September, 2012 at 6:57 am
Terence Tao
The rigorous version of this heuristic is given a few paragraphs later in the post.
20 September, 2012 at 7:51 am
Hahn
Thank you very much, Terence.
I got it.
21 October, 2012 at 6:23 am
Guo
Hallo, Prof. Tao, do you know if there’s any refinement of this theorem for the endpoint case, say in two dimension, the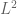 boundedness? Actually I’m thinking if the estimate
boundedness? Actually I’m thinking if the estimate  holds true, one motivation is that the counter-example we use in the 2D case
holds true, one motivation is that the counter-example we use in the 2D case 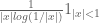 just misses being in
just misses being in  .
.
21 October, 2012 at 9:00 am
Terence Tao
I think this remains open. Schlag conjectured an estimate of this form (at least for a dyadically localised version of the maximal operator) in his 1998 Duke paper on the subject, but as far as I know it remains open. (A counterexample could potentially be constructed out of a very carefully designed Besicovitch set, but there might not actually be a set with all the required properties.)
24 October, 2012 at 10:34 pm
Terence Tao
Ah, well, this is embarrassing. A coauthor of mine has tactfully pointed out to me that a counterexample was in fact constructed in Proposition 1.5 of “Endpoint mapping properties of spherical maximal operators, by A. Seeger, T. Tao, and J. Wright, J. Inst. Math. Jussieu 2 (2003), 109-144. (But I was at least right that a Besicovitch set would be used in the counterexample…)
25 October, 2012 at 11:07 am
Guo
I checked the classical Besicovitch construction, and then believed the estimate to hold true, for 4 days :) Thanks a lot for the reference!
14 May, 2016 at 5:48 am
SAAD
Good morning,
how to demonstrate that the maximum according to Hardy-littlewood is integrable?
Best regards
8 June, 2016 at 2:50 am
khaled
Hello ,
Please i need your help, how to demonstrate that Hardy-littlewood function maximal is measurable ?
Best regards
8 June, 2016 at 10:08 am
Terence Tao
Establish this first for the modification of the Hardy-Littlewood maximal function in which the radii are constrained to be rational numbers.
8 June, 2016 at 3:17 am
Anonymous
Is it possible to extend theorem 1 by replacing the balls by an appropriate class of ellipsoids (and the spheres by appropriate spheroids) ?
8 June, 2016 at 10:07 am
Terence Tao
If one had some sort of hypothesis that every slice of the high-dimensional ball was “uniformly curved” in an appropriate sense, then one might be able to extend Stein’s argument to that case (certainly the spherical maximal function bound used extends to more general settings, see e.g. Chapter XI of Stein’s “Harmonic analysis”). But the argument is not able to deal with balls with flat or nearly flat portions of the boundary. There are other arguments in the literature (by Bourgain, Carbery, and Muller) that can deal at least partially with these cases, though.
24 May, 2017 at 2:07 am
Hardy-Littlewood maximal function | 江苏荣华投资公司
[…] Jump up to:a b Tao, Terence. “Stein’s spherical maximal theorem”.What’s New. Retrieved 22 May […]
28 October, 2017 at 4:50 pm
Z
Dear prof Tao;
Is finding the optimal constant for the Hardy-Littlewood inequality considered a “big problem “ in the field of harmonic analysis?
29 October, 2017 at 9:30 am
Terence Tao
Well, it would certainly be a great result if resolved (the one-dimensional case, for instance, was published in the Annals). But it is considered unlikely to be solved any time soon. There has been a lot of work though on dimension independent bounds, and I personally would be interested in knowing whether the weak-type 1,1 bound for the Hardy-Littlewood maximal function is dimension independent, having worked on this problem myself with Assaf Naor some time back. As is usual with these sorts of analysis problems, often it is not so much the result itself which would have interesting consequences, but the new methods of proof (in particular, one would hope that the techniques used to solve this problem can also give other dimension-independent bounds).
16 November, 2017 at 1:09 am
stmadfish (@stmadfish)
Hi Prof Tao,
I was wondering what is the sharp/optimal space of $f(x)$ for $A_r f(x)$ being continuous with respect to $r$. In your note (https://pdfs.semanticscholar.org/d001/3f6fdf52e6c6910f8da71d6bd47f2c092206.pdf), it seems that you just require $f$ to be non-nagative, bounded function with compact support. In this blog, you wrote “$A_r$ do not have good continuity properties in $r$.”
Thank you
16 November, 2017 at 1:36 am
stmadfish (@stmadfish)
I am sorry and I find the difference. In this post, $$A_r$$ is the spherical averaging operators , in the note, $$A_r$$ is the averaging operators. So your comment is no more confusing.
10 April, 2019 at 10:08 am
Basic Littlewood-Paley theory I | Almost Originality
[…] In developing a framework that allows to prove () we will encounter some variants of the square function above, including ones with smoother frequency projections that are useful in a variety of contexts. We will moreover show some applications of the above fact and its variants. One of these applications will be a proof of the boundedness of the spherical maximal function (almost verbatim the one on Tao’s blog). […]
19 April, 2019 at 6:00 am
Basic Littlewood-Paley theory III: applications | Almost Originality
[…] for dimension . Let me stress once again that the following is merely a slight re-elaboration of Tao’s excellent post on the […]
7 May, 2019 at 12:31 am
L
What if we replace by a convex body?
by a convex body?
7 May, 2019 at 8:40 am
Terence Tao
For arbitrary convex bodies, dimension-independent bounds for were established by Bourgain and independently by Carbery. It remains open to extend this to
were established by Bourgain and independently by Carbery. It remains open to extend this to 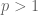 in general, but this was done for the
in general, but this was done for the 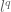 balls,
balls,  by Muller, with the endpoint
by Muller, with the endpoint 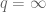 only achieved more recently in a 2014 paper of Bourgain.
only achieved more recently in a 2014 paper of Bourgain.
7 May, 2019 at 4:41 pm
L
Do you conceive possibility that these results are applicable in the optimization world?
18 April, 2020 at 6:12 am
Anonymous
In the case when , the book Functional Analysis by Stein-Shakarchi defines the averaging operator
, the book Functional Analysis by Stein-Shakarchi defines the averaging operator  as
as
which can be also read as the convolution . In the definition of
. In the definition of 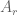 , the plus sign is used on the right instead. How should one understand the discrepancy?
, the plus sign is used on the right instead. How should one understand the discrepancy?
18 April, 2020 at 8:22 am
Terence Tao
The sphere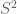 is symmetric under the reflection
is symmetric under the reflection 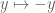 , so the choice of sign here does not matter.
, so the choice of sign here does not matter.
23 April, 2020 at 9:53 pm
Saurabh
Dear Prof. Tao,
I would like to know if there are some positive results for the spherical maximal function (including $n=2$) at the end-point. I could not find any in the literature.
24 April, 2020 at 3:16 pm
Terence Tao
Stein’s original paper has an example that shows that the strong-type estimate fails at the endpoint (see also p.472 of Stein’s “Harmonic analysis”). The restricted weak type estimate is also false, this is a special case of Proposition 1.5 of this paper of Seeger, Wright and myself.
24 April, 2020 at 6:34 pm
Saurabh
Thank you.
27 October, 2020 at 7:05 pm
Anonymous
Dear Prof.Tao.
I would like to know the way to extend a spherical maximal operator estimates on schwartz space to Lp space. Of course, i can extend the domain(Lp) of spherical maximal operator, but I think Proving the Inequality( llM(f)ll_p < C llfll_p) for general f in Lp needs some more setting.(because of nonlinearity)
28 October, 2020 at 2:37 pm
Terence Tao
See Chapter XI.3.5 of Stein’s “Harmonic analysis”. Basically while the maximal operator is not linear, it is still non-negative, monotone, sublinear, and also countably subadditive, and this plus some standard measure theory (e.g., outer and inner regularity of Lebesgue measure) will let one conclude. (It is convenient to work first with Borel-measurable functions rather than Lebesgue-measurable functions in order to guarantee measurability on all spheres (as opposed to almost all spheres), but as explained in Stein’s book, the conclusion ultimately holds for both types of measurability.)
12 September, 2022 at 2:59 pm
Anonymous
Dr. Tao:
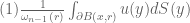 \\
\\
 \\
\\ with radius
with radius  , where (2) is the average over an annulus, i.e. the region of sphere centred at
, where (2) is the average over an annulus, i.e. the region of sphere centred at  with radius from
with radius from  to
to 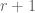 . Please explain.
. Please explain. with radius
with radius  ; I am not sure where you are getting the range
; I am not sure where you are getting the range  and
and 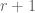 from. -T]
from. -T]
There are two equivalent definitions of spherical mean from Wikipedia\\
I don’t see how they are equivalent. (1) is the average over a sphere centred at
[The second integral is also on the sphere centred at
12 January, 2023 at 12:21 pm
Anonymous
Dear Professor Tao,
Is something known on the differentiability of the function when
when  is positive on a compact set with regular boundary and zero elsewhere? It certainly won’t hold for all
is positive on a compact set with regular boundary and zero elsewhere? It certainly won’t hold for all  but what about almost all of them in a compact interval? Do you by chance have any references? Thanks in advance
but what about almost all of them in a compact interval? Do you by chance have any references? Thanks in advance
13 January, 2023 at 6:22 am
Terence Tao
I would imagine that differentiability in is too much to hope for; however, one can probably use local smoothing estimates for the wave equation to obtain some Sobolev regularity in
is too much to hope for; however, one can probably use local smoothing estimates for the wave equation to obtain some Sobolev regularity in  . Some variational bounds are known: see https://arxiv.org/abs/2009.07366.
. Some variational bounds are known: see https://arxiv.org/abs/2009.07366.
16 January, 2023 at 2:32 am
Anonymous
Sorry for the lack of clarity, when speaking of differentiability of , the differentiability was to be understood with respect to
, the differentiability was to be understood with respect to  and not with respect to
and not with respect to  .
.