We continue our study of basic ergodic theorems, establishing the maximal and pointwise ergodic theorems of Birkhoff. Using these theorems, we can then give several equivalent notions of the fundamental concept of ergodicity, which (roughly speaking) plays the role in measure-preserving dynamics that minimality plays in topological dynamics. A general measure-preserving system is not necessarily ergodic, but we shall introduce the ergodic decomposition, which allows one to express any non-ergodic measure as an average of ergodic measures (generalising the decomposition of a permutation into disjoint cycles).
— The maximal ergodic theorem —
Just as we derived the mean ergodic theorem from the more abstract von Neumann ergodic theorem in the previous lecture, we shall derive the maximal ergodic theorem from the following abstract maximal inequality.
Theorem 1. (Dunford-Schwartz maximal inequality) Let
be a probability space, and let
be a linear operator with P1=1 and
(i.e.
for all
. Assume also that P maps non-negative functions to non-negative functions. Then the maximal function
obeys the inequality
(1)
for any
.
Proof. We can rewrite (1) as
. (2)
Since , we thus see (by replacing f with
) that we can reduce to proving (2) in the case
.
For every , consider the modified maximal function
. Observe that
if and only if
for all sufficiently large m. By the dominated convergence theorem, it thus suffices to show that
(3)
for all m. But observe from definition of (and the positivity preserving nature of P) that we have the pointwise recursive inequality
. (4)
Integrating this on the region and using the non-negativity of
, we obtain
. (6)
Since and
, the claim follows.
Applying this in the case when P is a shift operator, and replacing f by |f|, we obtain
Corollary 1. (Maximal ergodic theorem) Let
be a measure-preserving system. Then for any
and
one has
. (7)
Note that this inequality implies Markov’s inequality
. (8)
as a special case. Applying the real interpolation method, one also easily deduces the maximal inequality
(9)
for all , where the constant
depends on p (it blows up like
in the limit
).
Exercise 1 (Rising sun inequality). If , and
, establish the rising sun inequality
(10)
for any . (Hint: one can either adapt the proof of Theorem 1, or else partition the set appearing in (10) into disjoint intervals. The latter proof also leads to a proof of Corollary 1 which avoids the Dunford-Schwartz trick of introducing the functions
. The terminology “rising sun” comes from seeing how these intervals interact with the graph of the partial sums of f, which resembles the shadows cast on a hilly terrain by a rising sun.)
Exercise 2. (Transference principle) Show that Corollary 1 can be deduced directly from (10). (Hint: given , apply (10) to the functions
for each
(truncating the integers to a finite set if necessary), and then integrate in x using Fubini’s theorem.) This is an example of a transference principle between maximal inequalities on
and maximal inequalities on measure-preserving systems.
Exercise 3 (Stein-Stromberg maximal inequality). Derive a continuous version of the Dunford-Schwartz maximal inequality, in which the operators are replaced by a semigroup
acting on both
and
, in which the underlying measure space is only assumed to be
-finite rather than a probability space, and the averages
are replaced by
. Apply this continuous version with
equal to the heat operator on
for
to deduce the Stein-Stromberg maximal inequality
(11)
for all and
, where m is Lebesgue measure,
is the Euclidean ball of radius R centred at x, and the constant C is absolute (independent of d). This improves upon the Hardy-Littlewood maximal inequality, which gives the same estimate but with
replaced by
. It is an open question whether the dependence on d can be removed entirely; the estimate (11) is still the best known in high dimension. For d=1, the best constant C is known to be
, a result of Melas.
Remark 1. The study of maximal inequalities in ergodic theory is, of course, a subject in itself; a classical reference is this monograph of Stein.
— The pointwise ergodic theorem —
Using the maximal ergodic theorem and a standard limiting argument we can now deduce
Theorem 2 (Pointwise ergodic theorem). Let
be a measure-preserving system, and let
. Then for
-almost every
,
converges to
.
Proof. By subtracting from f if necessary, it suffices to show that
(12)
a.e. whenever . By telescoping series, (12) is already true when f takes the form
for some
. So by the arguments used to prove the von Neumann ergodic theorem from the previous lecture, we have already established the claim for a dense class of functions f in
with
, and thus also for a dense class of functions in
with
(since the latter space is dense in the former, and the
norm controls the
norm by the Cauchy-Schwarz inequality).
Now we use a standard limiting argument. Let with
. Then we can find a sequence
in the above dense class which converges in
to f. For almost every x, we thus have
(13)
for all j, and so by the triangle inequality we have
. (14)
But by Corollary 1 we see that the right-hand side of (14) converges to zero in measure as . Since the left-hand side does not depend on j, it must vanish almost everywhere, as required.
Remark 2. More generally, one can derive a pointwise convergence result on a class of rough functions by first establishing convergence for a dense subclass of functions, and then establishing a maximal inequality which is strong enough to allow one to take limits and establish pointwise convergence for all functions in the larger class. Conversely, principles such as Stein’s maximal principle indicate that in many cases this is in some sense the only way to establish such pointwise convergence results for rough functions.
Remark 3. Using the dominated convergence theorem (starting first with bounded functions f in order to get the domination), one can deduce the mean ergodic theorem from the pointwise ergodic theorem. But the converse is significantly more difficult; pointwise convergence for various ergodic averages is often a much harder result to establish than the corresponding norm convergence result (in particular, many of the techniques discussed in this course appear to be of sharply limited utility for pointwise convergence problems), and many questions in this area remain open.
Exercise 4 (Lebesgue differentiation theorem). Let with Lebesgue measure dm. Show that for almost every
, we have
, and in particular that
.
— Ergodicity —
Combining the mean ergodic theorem with the pointwise ergodic theorem (and with Exercises 7, 8 from the previous lecture) we have
Theorem 3 (Characterisations of ergodicity) Let
be a measure-preserving system. Then the following are equivalent:
- Any set
which is invariant (thus TE=E) has either full measure
or zero measure
.
- Any set
which is almost invariant (thus TE differs from E by a null set) has either full measure or zero measure.
- Any measurable function f with
a.e. is constant a.e.
- For any
and
, the averages
converge in
norm to
.
- For any two
, we have
.
- For any two measurable sets E and F, we have
.
- For any
, the averages
converge pointwise almost everywhere to
.
A measure-preserving system with any (and hence all) of the above properties is said to be ergodic.
Remark 4. Strictly speaking, ergodicity is a property that applies to a measure-preserving system . However, we shall sometimes abuse notation and apply the adjective “ergodic” to a single component of a system, such as the measure
or the shift T, when the other three components of the system are clear from context.
Here are some simple examples of ergodicity:
Example 1. If X is finite with uniform measure, then a shift map is ergodic if and only if it is a cycle.
Example 2. If a shift T is ergodic, then so is . However, from Example 1 we see that it is not necessarily true that
is ergodic for all n (this latter property is also known as total ergodicity).
Exercise 5. Show that the circle shift (with the usual Lebesgue measure) is ergodic if and only if
is irrational. (Hint: analyse the equation
for (say)
using Fourier analysis. Added, Feb 21: As pointed out to me in class, another way to proceed is to use the Lebesgue density theorem (or Lebesgue differentiation theorem) combined with Exercise 14 from Lecture 6.)
Exercise 6. Let be a standard Borel probability space. Show that the Bernoulli shift on the product system
is ergodic. (Hint: first establish property 6 of Theorem 3 when E and F each depend on only finitely many of the coordinates of
.)
Exercise 7. Let be an ergodic system. Show that if
is an eigenvalue of
, then
, the eigenspace
is one-dimensional, and that every eigenfunction f has constant magnitude |f| a.e.. Show that the the eigenspaces are orthogonal to each other in
, and the set of all eigenvalues of T forms an at most countable subgroup of the unit circle
.
Now we give a less trivial example of an ergodic system.
Proposition 1. (Ergodicity of skew shift) Let
be irrational. Then the skew shift
is ergodic.
Proof. Write the skew shift system as . To simplify the notation we shall omit the phrase “almost everywhere” in what follows.
We use an argument of Parry. If the system is not ergodic, then we can find a non-constant such that Tf = f. Next, we use Fourier analysis to write
, where
. Since f is T-invariant, and the vertical rotations
commute with T, we see that the
are also T-invariant. The function
depends only on the x variable, and so is constant by Exercise 5. So it suffices to show that
is zero for all non-zero m.
Fix m. We can factorise . The T-invariance of
now implies that
. If we then define
for
, we see that
, thus
is an eigenfunction of the circle shift with eigenvalue
. But this implies (by Exercise 7) that
is orthogonal to
for
close to zero. Taking limits we see that
is orthogonal to itself and must vanish; this implies that
and hence
vanish as well, as desired.
Exercise 8. Show that for any irrational and any
, the iterated skew shift system
is ergodic.
— Generic points —
Now let us suppose that we have a topological measure preserving system , i.e. a measure-preserving system
which is also a topological dynamical system
, with
the Borel
-algebra of T. Then we have the space C(X) of continuous (real or complex-valued) functions on X, which is dense inside
. From the Stone-Weierstrass theorem we also see that C(X) is separable.
A sequence in X is said to be uniformly distributed with respect to
if we have
(15)
for all . A point x in X is said to be generic if the forward orbit
is uniformly distributed.
Exercise 9. Let be a compact metrisable space with a Borel probability measure
, and let
be a sequence in X. Show that this sequence is uniformly distributed if and only if
for all open sets U in X with
. What happens if the hypothesis that the boundary of
has measure zero is removed?
From Theorem 3 and the separability of C(X) we obtain
Proposition 2. A topological measure-preserving system is ergodic if and only if almost every point is generic.
A topological measure-preserving system is said to be uniquely ergodic if every point is generic. The following exercise explains the terminology:
Exercise 10. Show that a topological measure-preserving system is uniquely ergodic if and only if the only T-invariant Borel probability measure on T is
. (Hint: use Lemma 1 from Lecture 7.) Because of this fact, one can sensibly define what it means for a topological dynamical system
to be uniquely ergodic, namely that it has a unique T-invariant Borel probability measure.
It is not always the case that an ergodic system is uniquely ergodic. For instance, in the Bernoulli system (with uniform measure on
, say), the point
is not generic. However, for more algebraic systems, it turns out that ergodicity and unique ergodicity are largely equivalent. We illustrate this with the circle and skew shifts:
Exercise 11. Show that the circle shift (with the usual Lebesgue measure) is uniquely ergodic if and only if
is irrational. (Hint: first show in the circle shift system that any translate of a generic point is generic.)
Proposition 3. (Unique ergodicity of skew shift) Let
be irrational. Then the skew shift
is uniquely ergodic.
Proof. We use an argument of Furstenberg. We again write the skew shift as . Suppose this system was not uniquely ergodic, then by Exercise 10 there is another shift-invariant Borel probability measure
. If we push
and
down to the circle shift system
by the projection map
, then by Exercises 10, 11 we must get the same measure. Thus
and
must agree on any set of the form
.
Let E denote the points in which are generic with respect to
; note that this set is Borel measurable. By Proposition 2, this set has full measure in
. Also, since the vertical rotations
commute with T and preserve
, we see that E must be invariant under such rotations; thus they are of the form
for some A. By the preceding discussion, we conclude that E also has full measure in
. But then (by the pointwise or mean ergodic theorem for
) we conclude that
-almost everywhere for every continuous f, and thus on integrating with respect to
we obtain
for every continuous f. But then by the Riesz representation theorem we have
, a contradiction.
Corollary 2. If
is irrational, then the sequence
is uniformly distributed in
(with respect to uniform measure).
Exercise 11a. Show that the systems considered in Exercise 8 are uniquely ergodic. Conclude that the exponent 2 in Corollary 2 can be replaced by any positive integer d.
Note that the topological dynamics theory developed in Lecture 6 only establishes the weaker statement that the above sequence is dense in rather than uniformly distributed. More generally, it seems that ergodic theory methods can prove topological dynamics results, but not vice versa. Here is another simple example of the same phenomenon:
Exercise 12. Show that a uniquely ergodic topological dynamical system (with the support of the measure equal to the whole space) is necessarily minimal. (The converse is not necessarily true, as already mentioned in Remark 6 of Lecture 7.)
— The ergodic decomposition —
Just as not every topological dynamical system is minimal, not every measure-preserving system is ergodic. Nevertheless, there is an important decomposition that allows one to represent non-ergodic measures as averages of ergodic measures. One can already see this in the finite case, when X is a finite set with the discrete -algebra, and
is a permutation on X, which can be decomposed as the disjoint union of cycles on a partition
of X. In this case, all shift-invariant probability measures take the form
(16)
where is the uniform probability measure on the cycle
, and
are non-negative constants adding up to 1. Each of the
are ergodic, but no non-trivial linear combination of these measures is ergodic. Thus we see in the finite case that every shift-invariant measure can be uniquely expressed as a convex combination of ergodic measures.
It turns out that a similar decomposition is available in general, at least if the underlying measure space is a compact topological space (or more generally, a Radon space). This is because of the following general theorem from measure theory.
Definition 1 (Probability kernel). Let
and
be measurable spaces. A probability kernel
is an assignment of a probability measure
on X to each
in such a way that the map
is measurable for every bounded measurable
.
Example 3. Every measurable map induces a probability kernel
. Every probability measure on X can be viewed as a probability kernel from a point to X. If
and
are two probability kernels from Y to Z and from X to Y respectively, their composition
is also a probability kernel, where
is the measure that assigns
to any measurable set E in Z. Thus one can view the class of measurable spaces and their probability kernels as a category, which includes the class of measurable spaces and their measurable maps as a subcategory.
Definition 2. (Regular space) A measurable space
is said to be regular if there exists a compact metrisable topology
on X for which
is the Borel
-algebra.
Example 4. Every topological measure-preserving system is regular.
Remark 5. Measurable spaces in which
is the Borel
-algebra of a topological space generated by a separable complete metric space (i.e. a Polish space) are known as standard Borel spaces. It is a non-trivial theorem from descriptive set theory that up to measurable isomorphism, there are only three types of standard Borel spaces: finite discrete spaces, countable discrete spaces, and the unit interval [0,1] with the usual Borel
-algebra. From this one can see that regular spaces are the same as standard Borel spaces, though we will not need this fact here.
Theorem 4 (Disintegration theorem). Let
and
be probability spaces, with
regular. Let
be a morphism (thus
). Then there exists a probability kernel
such that
(17)
for any bounded measurable
and
. Also, for any such g, we have
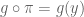
-a.e. (18)
for
-a.e. y.
Furthermore, this probability kernel is unique up to
-almost everywhere equivalence, in the sense that if
is another probability kernel with the same properties, then
for
-almost every
.
We refer to the probability kernel generated by the above theorem as the disintegration of
relative to the factor map
.
Proof. We begin by proving uniqueness. Suppose we have two probability kernels with the above properties. Then on subtraction we have
(19)
for all bounded measurable ,
. Specialising to
for some measurable set
, we conclude that
for
-almost every y. Since
is regular, it is separable and we conclude that
for
-almost every y, as required.
Now we prove existence. The pullback map defined by
has an adjoint
, thus
(20)
for all and
. It is easy to see from duality that we have
for all
(where we select a compact metrisable topology that generates the regular
-algebra
). Recall that
is not quite a measurable function, but is instead an equivalence class of measurable functions modulo
-almost everywhere equivalence. Since C(X) is separable, we find a measurable representative
of
to every
which varies linearly with f, and is such that
for all y outside of a set E of
-measure zero and for all
. For all such y, we can then apply the Riesz representation theorem to obtain a Radon probability measure
such that
(21)
for all such y. We set equal to some arbitrarily fixed Radon probability measure for
. We then observe that the required properties (including the measurability of
) are already obeyed for
. To generalise this to bounded measurable f, observe that the class
of f obeying the required properties is closed under dominated pointwise convergence, and so contains the indicator functions of open or compact sets (by Urysohn’s lemma). Applying dominated pointwise convergence again and inner and outer regularity, we see that the indicator functions of any Borel set lies in
. Thus all simple measurable functions lie in
, and on taking uniform limits we obtain the claim.
Finally, we prove (18). From two applications of (17) we have
(22)
for all bounded measurable and
. The claim follows (using the separability of the space of all f).
Exercise 13. Let the notation and assumptions be as in Theorem 4. Suppose that is also regular, and that the map
is continuous with respect to some compact metrisable topologies that generate
and
respectively. Then show that for
-almost every y, the probability measure
is supported in
.
Proposition 4 (Ergodic decomposition). Let
be a regular measure-preserving system. Let
be the system defined by
,
,
, and
, and let
be the identity map. Let
be the disintegration of
with respect to the factor map
. Then for
-almost every y, the measure
is T-invariant and ergodic.
Proof. Observe from the T-invariance of
(and of
) that the probability kernel
would also be a disintegration of
. Thus we have
for
-almost every y.
Now we show the ergodicity. As the space of bounded measurable is separable, it suffices by Theorem 3 and a limiting argument to show that for any fixed such f, the averages
converge pointwise
-a.e. to
for
-a.e. y.
From the pointwise ergodic theorem, we already know that converges to
outside of a set of
-measure zero. By (17), this set also has
-measure zero for
-almost every y. Thus it will suffice to show that
is
-a.e. equal to
for
-a.e. y. Now observe that
, so the claim follows from (18) and (21).
Exercise 14. Let be a separable measurable space, and let T be bimeasurable bijection
. Let
denote the Banach space of all finite measures on
with the total variation norm. Let
denote the collection of probability measures on
which are T-invariant. Show that this is a closed convex subset of
, and the extreme points of
are precisely the ergodic probability measures (which also form a closed subset of
). We remark that one can use these facts to prove some variants of Proposition 4 using Choquet’s theorem, although I do not know of a way to prove this proposition in full generality just from Choquet.
Exercise 15. Show that a topological measure-preserving system is uniquely ergodic if and only if the only ergodic shift-invariant Borel probability measure on X is
.

83 comments
Comments feed for this article
27 September, 2018 at 4:16 pm
Abhishek Khetanhek
Dear Professor Tao,
In the second paragraph of the proof of Proposition 4 (ergodic decomposition theorem) there is a line which reads “it suffices by Theorem 3 and a limiting argument …” I am not able to follow the sufficiency. Can you please provide some details. Thank you.
2 October, 2018 at 4:21 pm
Terence Tao
One can find a countable set of bounded measurable functions that is dense in every
of bounded measurable functions that is dense in every  ; indeed one can take
; indeed one can take  to be rational linear combinations of indicator functions of the countable generating set of the sigma-algebra.
to be rational linear combinations of indicator functions of the countable generating set of the sigma-algebra.
By hypothesis and countable union, we see that for -almost every
-almost every  , the pointwise ergodic theorem holds in
, the pointwise ergodic theorem holds in 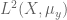 for every
for every  . By a limiting argument, that shows that the mean ergodic theorem holds in
. By a limiting argument, that shows that the mean ergodic theorem holds in 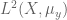 for every
for every 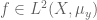 , hence by Theorem 3,
, hence by Theorem 3, 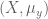 is ergodic.
is ergodic.
7 October, 2018 at 11:58 am
Abhishek Khetanhek
Thank you for the detailed response.
6 March, 2019 at 8:30 am
Yuping Zhang
My conclusion: The Dr. Terence Tao’s the blue-eyed islanders puzzle only works out if N=2, N=1, and in condition N=0 ( see below)
The example 1) explain 2 colors in the puzzle .
The case, 10 and N=1, and N= is the only person to whose eyes are not green. Rest of the 9 are greens.
Someone announced: ”At least one of the ten has green eyes.”
In the 9th days, CAN all of the 9 greens figure it out their eye color logically? NO
The example 2) explain 2 colors in the puzzle
The case, 10 and N=0 or the entire ten has no green eyes
Someone announced:”At least one of the ten has no green eyes.
In the 10th days, CAN all of the 10 no greens figure it out their eye color logically? YES.
Why? Again!
the crucial key is the entire 10 of them could see the single color in the same amount of people=9, therefore, it’s not leaving each day that tells more and more works out.
But not in Dr. Terence Tao’s the blue-eyed island puzzle.
15 March, 2019 at 8:16 am
Maths student
Dear Prof. Tao,
in the proof of uniqueness in the disintegration theorem, do you really mean to say that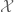 is regular? Or do you mean that under a suitable metric,
is regular? Or do you mean that under a suitable metric,  is separable?
is separable?
15 March, 2019 at 8:22 am
Maths student
I see, what you mean is that regularity is in fact a property of the -algebra. Perhaps this should be pointed out.
-algebra. Perhaps this should be pointed out.
[See Definition 2 – T.]
11 January, 2020 at 7:45 am
Radu Zaharopol
Dear Professor Tao,
Have you had a chance to see Daniel Worm’s Ph.D. thesis (Leiden 2010) and my 2014 Springer monograph?
In these works we discuss the KBBY (Kryloff-Bogoliouboff-Beboutoff-Yosida) ergodic decomposition. The KBBY decomposition is obtained in a constructive manner, while the decomposition based on the Choquet-Phelps approach is highly nonconstructive.
4 January, 2021 at 4:21 pm
Fausto Di Biase
In Remark 5 you say that ”regular spaces are the same as standard Borel spaces”, but a countably infinite discrete space is a standard Borel space but it is not compact, hence it is not a regular space. I am confused. Could you please help? Thanks.
4 January, 2021 at 7:35 pm
Terence Tao
A countably infinite discrete space is measurably (though not topologically) equivalent to the countable compact set , so it (or more precisely, the measurable space associated to it) is a regular space. (The topology used in the definition of a regular space is not necessarily the one that one may initially wish to assign to the measurable space in question.)
, so it (or more precisely, the measurable space associated to it) is a regular space. (The topology used in the definition of a regular space is not necessarily the one that one may initially wish to assign to the measurable space in question.)
5 January, 2021 at 7:50 am
Fausto Di Biase
Thanks a lot!
18 September, 2023 at 12:40 am
Anonymous
Line (18) in the statement of the disintegration theorem doesn’t quite seem to make sense.
On the RHS $g(y)$ is a complex number afaict. And $g \circ \pi$ is a function on $X$. It is also followed by two ‘a.e.’ statements.
18 September, 2023 at 1:48 am
Anonymous
OK scratch that; it makes sense, I just couldn’t parse the way it was written.
The following statement is true for nu-a.e. y: For mu_y a.e. x, we have that g(\pi(x)) = g(y).
22 September, 2023 at 12:38 am
Anonymous
In Exercise 13, why do you need ‘compact’??