One of the fundamental structures in modern mathematics is that of a group. Formally, a group is a set equipped with an identity element
, a multiplication operation
, and an inversion operation
obeying the following axioms:
- (Closure) If
, then
and
are well-defined and lie in
. (This axiom is redundant from the above description, but we include it for emphasis.)
- (Associativity) If
, then
.
- (Identity) If
, then
.
- (Inverse) If
, then
.
One can also consider additive groups instead of multiplicative groups, with the obvious changes of notation. By convention, additive groups are always understood to be abelian, so it is convenient to use additive notation when one wishes to emphasise the abelian nature of the group structure. As usual, we often abbreviate
by
(and
by
) when there is no chance of confusion.
If furthermore is equipped with a topology, and the group operations
are continuous in this topology, then
is a topological group. Any group can be made into a topological group by imposing the discrete topology, but there are many more interesting examples of topological groups, such as Lie groups, in which
is not just a topological space, but is in fact a smooth manifold (and the group operations are not merely continuous, but also smooth).
There are many naturally occuring group-like objects that obey some, but not all, of the axioms. For instance, monoids are required to obey the closure, associativity, and identity axioms, but not the inverse axiom. If we also drop the identity axiom, we end up with a semigroup. Groupoids do not necessarily obey the closure axiom, but obey (versions of) the associativity, identity, and inverse axioms. And so forth.
Another group-like concept is that of a local topological group (or local group, for short), which is essentially a topological group with the closure axiom omitted (but do not obey the same axioms set as groupoids); they arise primarily in the study of local properties of (global) topological groups, and also in the study of approximate groups in additive combinatorics. Formally, a local group is a topological space
equipped with an identity element
, a partially defined but continuous multiplication operation
for some domain
, and a partially defined but continuous inversion operation
, where
, obeying the following axioms:
- (Local closure)
is an open neighbourhood of
, and
is an open neighbourhood of
.
- (Local associativity) If
are such that
and
are both well-defined, then they are equal. (Note however that it may be possible for one of these products to be defined but not the other, in contrast for instance with groupoids.)
- (Identity) For all
,
.
- (Local inverse) If
and
is well-defined, then
. (In particular this, together with the other axioms, forces
.)
We will often refer to ordinary groups as global groups (and topological groups as global topological groups) to distinguish them from local groups. Every global topological group is a local group, but not conversely.
One can consider discrete local groups, in which the topology is the discrete topology; in this case, the openness and continuity axioms in the definition are automatic and can be omitted. At the other extreme, one can consider local Lie groups, in which the local group has the structure of a smooth manifold, and the group operations are smooth. We can also consider symmetric local groups, in which
(i.e. inverses are always defined). Symmetric local groups have the advantage of local homogeneity: given any
, the operation of left-multiplication
is locally inverted by
near the identity, thus giving a homeomorphism between a neighbourhood of
and a neighbourhood of the identity; in particular, we see that given any two group elements
in a symmetric local group
, there is a homeomorphism between a neighbourhood of
and a neighbourhood of
. (If the symmetric local group is also Lie, then these homeomorphisms are in fact diffeomorphisms.) This local homogeneity already simplifies a lot of the possible topology of symmetric local groups, as it basically means that the local topological structure of such groups is determined by the local structure at the origin. (For instance, all connected components of a local Lie group necessarily have the same dimension.) It is easy to see that any local group has at least one symmetric open neighbourhood of the identity, so in many situations we can restrict to the symmetric case without much loss of generality.
A prime example of a local group can be formed by restricting any global topological group to an open neighbourhood
of the identity, with the domains
and
one easily verifies that this gives the structure of a local group (which we will sometimes call
to emphasise the original group
). If
is symmetric (i.e.
), then we in fact have a symmetric local group. One can also restrict local groups
to open neighbourhoods
to obtain a smaller local group
by the same procedure (adopting the convention that statements such as
or
are considered false if the left-hand side is undefined). (Note though that if one restricts to non-open neighbourhoods of the identity, then one usually does not get a local group; for instance
is not a local group (why?).)
Finite subsets of (Hausdorff) groups containing the identity can be viewed as local groups. This point of view turns out to be particularly useful for studying approximate groups in additive combinatorics, a point which I hope to expound more on later. Thus, for instance, the discrete interval is an additive symmetric local group, which informally might model an adding machine that can only handle (signed) one-digit numbers. More generally, one can view a local group as an object that behaves like a group near the identity, but for which the group laws (and in particular, the closure axiom) can start breaking down once one moves far enough away from the identity.
One can formalise this intuition as follows. Let us say that a word in a local group
is well-defined in
(or well-defined, for short) if every possible way of associating this word using parentheses is well-defined from applying the product operation. For instance, in order for
to be well-defined,
,
,
,
, and
must all be well-defined. In the preceding example
,
is not well-defined because one of the ways of associating this sum, namely
, is not well-defined (even though
is well-defined).
Exercise 1 (Iterating the associative law)
- Show that if a word
in a local group is well-defined, then all ways of associating this word give the same answer, and so we can uniquely evaluate
as an element in
.
- Give an example of a word
in a local group which has two ways of being associated that are both well-defined, but give different answers. (Hint: the local associativity axiom prevents this from happening for
, so try
. A small discrete local group will already suffice to give a counterexample; verifying the local group axioms are easier if one makes the domain of definition of the group operations as small as one can get away with while still having the counterexample.)
Exercise 2 Show that the number of ways to associate a word
is given by the Catalan number
.
Exercise 3 Let
be a local group, and let
be an integer. Show that there exists a symmetric open neighbourhood
of the identity such that every word of length
in
is well-defined in
(or more succinctly,
is well-defined). (Note though that these words will usually only take values in
, rather than in
, and also the sets
tend to become smaller as
increases.)
In many situations (such as when one is investigating the local structure of a global group) one is only interested in the local properties of a (local or global) group. We can formalise this by the following definition. Let us call two local groups and
locally identical if they have a common restriction, thus there exists a set
such that
(thus,
, and the topology and group operations of
and
agree on
). This is easily seen to be an equivalence relation. We call an equivalence class
of local groups a group germ.
Let be a property of a local group (e.g. abelianness, connectedness, compactness, etc.). We call a group germ locally
if every local group in that germ has a restriction that obeys
; we call a local or global group
locally
if its germ is locally
(or equivalently, every open neighbourhood of the identity in
contains a further neighbourhood that obeys
). Thus, the study of local properties of (local or global) groups is subsumed by the study of group germs.
Exercise 4
- Show that the above general definition is consistent with the usual definitions of the properties “connected” and “locally connected” from point-set topology.
- Strictly speaking, the above definition is not consistent with the usual definitions of the properties “compact” and “local compact” from point-set topology because in the definition of local compactness, the compact neighbourhoods are certainly not required to be open. Show however that the point-set topology notion of “locally compact” is equivalent, using the above conventions, to the notion of “locally precompact inside of an ambient local group”. Of course, this is a much more clumsy terminology, and so we shall abuse notation slightly and continue to use the standard terminology “locally compact” even though it is, strictly speaking, not compatible with the above general convention.
- Show that a local group is discrete if and only if it is locally trivial.
- Show that a connected global group is abelian if and only if it is locally abelian. (Hint: in a connected global group, the only open subgroup is the whole group.)
- Show that a global topological group is first-countable if and only if it is locally first countable. (By the Birkhoff-Kakutani theorem, this implies that such groups are metrisable if and only if they are locally metrisable.)
- Let
be a prime. Show that the solenoid group
, where
is the
-adic integers and
is the diagonal embedding of
inside
, is connected but not locally connected.
Remark 1 One can also study the local properties of groups using nonstandard analysis. Instead of group germs, one works (at least in the case when
is first countable) with the monad
of the identity element
of
, defined as the nonstandard group elements
in
that are infinitesimally close to the origin in the sense that they lie in every standard neighbourhood of the identity. The monad
is closely related to the group germ
, but has the advantage of being a genuine (global) group, as opposed to an equivalence class of local groups. It is possible to recast most of the results here in this nonstandard formulation; see e.g. the classic text of Robinson. However, we will not adopt this perspective here.
A useful fact to know is that Lie structure is local. Call a (global or local) topological group Lie if it can be given the structure of a (global or local) Lie group.
Lemma 1 (Lie is a local property) A global topological group
is Lie if and only if it is locally Lie. The same statement holds for local groups
as long as they are symmetric.
We sketch a proof of this lemma below the fold. One direction is obvious, as the restriction a global Lie group to an open neighbourhood of the origin is clearly a local Lie group; for instance, the continuous interval is a symmetric local Lie group. The converse direction is almost as easy, but (because we are not assuming
to be connected) requires one non-trivial fact, namely that local homomorphisms between local Lie groups are automatically smooth; details are provided below the fold.
As with so many other basic classes of objects in mathematics, it is of fundamental importance to specify and study the morphisms between local groups (and group germs). Given two local groups , we can define the notion of a (continuous) homomorphism
between them, defined as a continuous map with
such that whenever are such that
is well-defined, then
is well-defined and equal to
; similarly, whenever
is such that
is well-defined, then
is well-defined and equal to
. (In abstract algebra, the continuity requirement is omitted from the definition of a homomorphism; we will call such maps discrete homomorphisms to distinguish them from the continuous ones which will be the ones studied here.)
It is often more convenient to work locally: define a local (continuous) homomorphism from
to
to be a homomorphism from an open neighbourhood
of the identity to
. Given two local homomorphisms
,
from one pair of locally identical groups
to another pair
, we say that
are locally identical if they agree on some open neighbourhood of the identity in
(note that it does not matter here whether we require openness in
, in
, or both). An equivalence class
of local homomorphisms will be called a germ homomorphism (or morphism for short) from the group germ
to the group germ
.
Exercise 5 Show that the class of group germs, equipped with the germ homomorphisms, becomes a category. (Strictly speaking, because group germs are themselves classes rather than sets, the collection of all group germs is a second-order class rather than a class, but this set-theoretic technicality can be resolved in a number of ways (e.g. by restricting all global and local groups under consideration to some fixed “universe”) and should be ignored for this exercise.)
As is usual in category theory, once we have a notion of a morphism, we have a notion of an isomorphism: two group germs are isomorphic if there are germ homomorphisms
,
that invert each other. Lifting back to local groups, the associated notion is that of local isomorphism: two local groups
are locally isomorphic if there exist local isomorphisms
and
from
to
and from
to
that locally invert each other, thus
for
sufficiently close to
, and
for
sufficiently close to
. Note that all local properties of (global or local) groups that can be defined purely in terms of the group and topological structures will be preserved under local isomorphism. Thus, for instance, if
are locally isomorphic local groups, then
is locally connected iff
is,
is locally compact iff
is, and (by Lemma 1)
is Lie iff
is.
Exercise 6
Show that the additive global groups and
are locally isomorphic.
Show that every locally path-connected group is locally isomorphic to a path-connected, simply connected group.
— 1. Lie’s third theorem —
Lie’s fundamental theorems of Lie theory link the Lie group germs to Lie algebras. Observe that if is a locally Lie group germ, then the tangent space
at the identity of this germ is well-defined, and is a finite-dimensional vector space. If we choose
to be symmetric, then
can also be identified with the left-invariant (say) vector fields on
, which are first-order differential operators on
. The Lie bracket for vector fields then endows
with the structure of a Lie algebra. It is easy to check that every morphism
of locally Lie germs gives rise (via the derivative map at the identity) to a morphism
of the associated Lie algebras. From the Baker-Campbell-Hausdorff formula (which is valid for local Lie groups, as discussed in this previous post) we conversely see that
uniquely determines the germ homomorphism
. Thus the derivative map provides a covariant functor from the category of locally Lie group germs to the category of (finite-dimensional) Lie algebras. In fact, this functor is an isomorphism, which is part of a fact known as Lie’s third theorem:
Theorem 2 (Lie’s third theorem) For this theorem, all Lie algebras are understood to be finite dimensional (and over the reals).
- Every Lie algebra
is the Lie algebra of a local Lie group germ
, which is unique up to germ isomorphism (fixing
).
- Every Lie algebra
is the Lie algebra of some global connected, simply connected Lie group
, which is unique up to Lie group isomorphism (fixing
).
- Every homomorphism
between Lie algebras is the derivative of a unique germ homomorphism
between the associated local Lie group germs.
- Every homomorphism
between Lie algebras is the derivative of a unique Lie group homomorphism
between the associated global connected, simply connected, Lie groups.
- Every local Lie group germ is the germ of a global connected, simply connected Lie group
, which is unique up to Lie group isomorphism. In particular, every local Lie group is locally isomorphic to a global Lie group.
We record the (standard) proof of this theorem below the fold, which is ultimately based on Ado’s theorem and the Baker-Campbell-Hausdorff formula. Lie’s third theorem (which, actually, was proven in full generality by Cartan) demonstrates the equivalence of three categories: the category of finite-dimensonal Lie algebras, the category of local Lie group germs, and the category of connected, simply connected Lie groups.
— 2. Globalising a local group —
Many properties of a local group improve after passing to a smaller neighbourhood of the identity. Here are some simple examples:
Exercise 7 Let
be a local group.
- Give an example to show that
does not necessarily obey the cancellation laws
for
(with the convention that statements such as
are false if either side is undefined). However, show that there exists an open neighbourhood
of
within which the cancellation law holds.
- Repeat the previous part, but with the cancellation law (1) replaced by the inversion law
for any
for which both sides are well-defined.
- Repeat the previous part, but with the inversion law replaced by the involution law
for any
for which the left-hand side is well-defined.
Note that the counterexamples in the above exercise demonstrate that not every local group is the restriction of a global group, because global groups (and hence, their restrictions) always obey the cancellation law (1), the inversion law (2), and the involution law (3). Another way in which a local group can fail to come from a global group is if it contains relations which can interact in a “global’ way to cause trouble, in a fashion which is invisible at the local level. For instance, consider the open unit cube , and consider four points
in this cube that are close to the upper four corners
of this cube respectively. Define an equivalence relation
on this cube by setting
if
and
is equal to either
or
for some
. Note that this indeed an equivalence relation if
are close enough to the corners (as this forces all non-trivial combinations
to lie outside the doubled cube
). The quotient space
(which is a cube with bits around opposite corners identified together) can then be seen to be a symmetric additive local Lie group, but will usually not come from a global group. Indeed, it is not hard to see that if
is the restriction of a global group
, then
must be a Lie group with Lie algebra
(by Lemma 1), and so the connected component
of
containing the identity is isomorphic to
for some sublattice
of
that contains
; but for generic
, there is no such lattice, as the
will generate a dense subset of
. (The situation here is somewhat analogous to a number of famous Escher prints, such as Ascending and Descending, in which the geometry is locally consistent but globally inconsistent.) We will give this sort of argument in more detail below the fold (see the proof of Proposition 7).
Nevertheless, the space is still locally isomorphic to a global Lie group, namely
; for instance, the open neighbourhood
is isomorphic to
, which is an open neighbourhood of
. More generally, Lie’s third theorem tells us that any local Lie group is locally isomorphic to a global Lie group.
Let us call a local group globalisable if it is locally isomorphic to a global group; thus Lie’s third theorem tells us that every local Lie group is globalisable. Thanks to Goldbring’s solution to the local version of Hilbert’s fifth problem, we also know that locally Euclidean local groups are globalisable. A modification of this argument by van den Dries and Goldbring shows in fact that every locally compact local group is globalisable.
In view of these results, it is tempting to conjecture that all local groups are globalisable;; among other things, this would simplify the proof of Lie’s third theorem (and of the local version of Hilbert’s fifth problem). Unfortunately, this claim as stated is false:
Theorem 3 There exists local groups
which are not globalisable.
The counterexamples used to establish Theorem 3 are remarkably delicate; the first example I know of is due to van Est and Korthagen. One reason for this, of course, is that the previous results prevents one from using any local Lie group, or even a locally compact group as a counterexample. We will present a (somewhat complicated) example below, based on the unit ball in the infinite-dimensional Banach space .
However, there are certainly many situations in which we can globalise a local group. For instance, this is the case if one has a locally faithful representation of that local group inside a global group:
Lemma 4 (Faithful representation implies globalisability) Let
be a local group, and suppose there exists an injective local homomorphism
from
into a global topological group
with
symmetric. Then
is isomorphic to the restriction of a global topological group to an open neighbourhood of the identity; in particular,
is globalisable.
The material here is based in part on this paper of Olver and this paper of Goldbring.
— 3. Globalisation —
We begin by proving Lemma 4. Let be as in that lemma. The set
generates a subgroup
of
, which contains an embedded copy
of
. It is then tempting to restrict the topology of
to that of
to give
the structure of a global topological group and then declare victory, but the difficulty is that
need not be an open subset of
, as the following key example demonstrates.
Example 1 Take
,
, and
, where
is an irrational number (e.g.
). Then
is the dense subgroup
of
, which is not locally isomorphic to
if endowed with the topology inherited from
(for instance,
is not locally connected in this topology, whereas
is). Also,
, while homeomorphic to
, is not an open subset of
. Thus we see that the “global” behaviour of
, as captured by the group
, can be rather different from the “local” structure of
.
However, the problem can be easily resolved by giving a different topology, as follows. We use the sets
as a neighbourhood base for the identity in
, and their left-translates
as a neighbourhood base for any other element
of
. This is easily seen to generate a topology. To show that the group operations remain continuous in this topology, the main task is to show that the conjugation operations
are continuous with respect to the neighbourhood base at the identity, in the sense that for every open neighbourhood
of the identity in
and every
, there exists an open neighbourhood
of the identity such that
. But for
this is clear from the injective local homomorphism properties of
(after shrinking
small enough that
will still fall in
), and then an induction shows the same is true for
in any product set
of
, and hence in all of
. (It is instructive to follow through this argument for the example given above.)
There is another characterisation of globalisability, due to Mal’cev, which is stronger than Lemma 4, but this strengthening is usually not needed in applications. Call a local group globally associative if, whenever
and there are two ways to associate the product
which are individually well-defined, then the value obtained by these two associations are equal to each other. This implies but is stronger than local associativity (which only covers the cases
).
Proposition 5 (Globalisation criterion) Let
be a symmetric local group. Then
is isomorphic to (a restriction of) an open symmetric neighbourhood of the identity in a global topological group if and only if it is globally associative.
By “restriction of an open symmetric neighbourhood of the identity “, I mean the local group formed from
by restricting the set
of admissible products for the local group law to some open neighbourhood of
in
.
Proof: The “only if” direction is clear, so now suppose that is a globally associative symmetric local group. Let us call a formal product
with
weakly well-defined if there is at least one way to associate the product so that it can be defined in
(this is opposed to actual well-definedness of
, which requires all associations to be well-defined). By global associativity, the product
has a unique evaluation in
whenever it is weakly well-defined.
Let be the (discrete) free group generated by the elements of
(now viewed merely as a discrete set), thus each element of
can be expressed as a formal product
of elements
in
and their formal inverses
, where
, and
can be viewed (only as a set, not as a local group) as a subset of
. Let
be the set of elements in
that have at least one representation (not necessarily reduced) of the form
such that
and
with
weakly well-defined and evaluating to the identity in
. It is easy to see that
is a normal subgroup of
, and so we may form the quotient group
and the quotient map
. We claim
is injective on
, and so
is isomorphic (as a discrete local group) to
. To see this, suppose for contradiction that there are distinct
such that
, thus
for some
. As this identity takes place in the free group
, this implies that the formal word
can be reduced to the generator
of
by a finite number of operations in which an adjacent pair of the form
or
for some
, or a singleton of the form
, is deleted. In particular, this implies that
is weakly well-defined and evaluates to
in
. On other hand, as
, we also see (by associating in a different way) that
is weakly well-defined and evaluates to
in
. This contradicts global associativity, and the claim follows.
To conclude the proof, we need to place a topology on that makes
homeomorphic to
. This can be done by taking the sets
, with
an open neighbourhood of the identity in
, as a neighbourhood base for each
. By arguing as in the proof of Lemma 4 one can verify that this generates a topology that makes
a topological group, and makes
homeomorphic to
; we leave the details as an exercise.
Exercise 8 Complete the proof of the above proposition.
Exercise 9 Use Proposition 5 to give an alternate proof of Proposition 4.
— 4. Globalising Lie structure —
To prove Theorem 1 we need the following basic lemma:
Lemma 6 (Continuity implies smoothness for local Lie homomorphisms) Let
be a local homomorphism between two local Lie groups
. Then
is smooth near the origin. If
is symmetric, then
is in fact smooth on all of
.
Proof: Define a local one-parameter subgroup of to be a germ homomorphism
from the additive germ
to
; for any sufficiently small
, this is associated with a continuous homomorphism
of local groups. Note that for any sufficiently small
, we have
for all natural numbers . Working in exponential coordinates in a sufficiently small neighbourhood of
, for which we have a smooth logarithm map to the Lie algebra
, we have
for all sufficiently small , which implies in particular that
for all sufficiently small positive with
rational. By continuity we may omit the rationality hypothesis, and we conclude that there exists a unique
such that
for all small positive
; since
for sufficiently small
as well, this is also true for small negative
. Thus we have
for all sufficiently small
. Conversely, every element
of
generates a local one-parameter subgroup in this fashion.
The map clearly takes local one-parameter subgroups of
to one-parameter subgroups of
, thus defining a “derivative” map
. It is easy to see that this map is continuous; using the law
we also verify that this map is an additive homomorphism, and is hence linear (and in particular is smooth). For sufficiently small ,
is then given by the formula
which is manifestly smooth near the identity. If is symmetric, we can then use local homogeneity to make
symmetric at all points of
.
Remark 2 By using the Baker-Campbell-Hausdorff formula, we can upgrade the smoothness here to real analyticity.
Now we sketch the proof of Theorem 1. Clearly, every global Lie group is locally Lie as well. Conversely, if is locally Lie, then we have at least one smooth coordinate chart for
near the origin. Also, from the above lemma, all conjugation maps
for a given
are smooth for a sufficiently small neighbourhood of the origin in this chart (we allow this neighbourhood to depend on
, but for
in a compact set it is easy to see that we can take the neighbourhood to be uniform). We can translate the smooth chart around by left-invariance to give an atlas for all of
; the smooth compatibility of the charts with each other is easily established using the local smoothness of the conjugation map (shrinking the chart if necessary first). The smoothness of the group operations are proven similarly.
Exercise 10 Fill out the details in the above proof.
Now we can prove Lie’s third theorem. Part 5 follows from Parts 1-4, so we focus on the first four parts. We first dispose of uniqueness, which is easy. From the formula (4) we see that uniquely determines
locally, which gives the uniqueness claims in Part 3. A monodromy argument then shows that
is also uniquely determined if
is connected and simply connected, giving the uniqueness claim in Part 4. The uniqueness claims in Parts 1-2 then follow from those in Parts 3-4.
Now we turn to existence. We establish this first for Parts 1 and 2. Let be a Lie algebra. Applying Ado’s theorem (discussed in this blog post), we can identify
with a subalgebra of the Lie algebra
for some finite
. If
is a small symmetric neighbourhood of the identity in
, we can then form the exponential
, which (as the exponential map is a local diffeomorphism) is a submanifold of
. Applying the Baker-Campbell-Hausdorff formula in
, we see that
is a local group (because
, and
will lie in
for
in
and
sufficiently small, or vice versa). This already gives Part 1; as
clearly has a faithful representation in
, we may use Lemma 4 (and Lemma 1) to extend
to a global Lie group, giving Part 2.
Existence in Part 3 follows from (4) and the Baker-Campbell-Hausdorff formula; extending the germ homorphism to a Lie group homomorphism on the connected, simply connected Lie group then follows by a standard monodromy argument, giving Part 4. This completes the proof of Lie’s third theorem.
Remark 3 The full strength of Ado theorem was not needed here. For instance, knowing Ado’s theorem for nilpotent Lie algebras already suffices to establish Lie’s third theorem in the nilpotent case. By considering the free nilpotent groups and letting the step go to infinity, this shows that the Baker-Campbell-Hausdorff-Dynkin formula is formally associative (and hence associative, due to the absolute convergence of the formula), which already suffices to construct the local Lie group and thence the global Lie group.
On the other hand, it is possible to eliminate the reliance on the Baker-Campbell-Hausdorff formula by using Frobenius’s theorem to construct the local Lie group instead; we omit the details.
Remark 4 The above argument also reveals one advantage of local Lie groups over global ones; local Lie groups are locally linearisable (in the sense that they are isomorphic to a local subgroup of a linear group), whereas global Lie groups need not be globally linearisable, as discussed in this previous post.
— 5. A non-globalisable group —
We now prove Theorem 3. We begin with a preliminary construction, which gives a local group that has a fixed small neighbourhood that cannot arise from a global group.
Proposition 7 (Preliminary counterexample) For any
, there exists an equivalence relation
on the open unit ball
of
which gives
the structure of a local group, but such that
is not isomorphic (even as a discrete local group) to a subset of a global group.
Proof: We will use a probabilistic construction, mimicking the three-dimensional example from the introduction. Fix
, and let
be a large integer (depending on
) to be chosen later. We identify the
-dimensional cube
with the unit ball in
, which embeds in the unit ball in
via extension by zero. Let
be randomly chosen corners of this cube. A simple application of the union bound shows that with probability approaching
as
, we have
for all
, but also that for any
and any choice of signs
, the vectors
agree on at least one coordinate. As a corollary of this, we see that
for any integers with
.
Let be a small number (depending on
,
) to be chosen later. We let
be an element of
which is within distance
of
, then we have
(allowing implied constants to depend on ) for
as above. By generically perturbing the
, we may assume that they are noncommensurable in the sense that span a dense subset of
. In particular, the
are linearly independent over
.
We now define an equivalence relation on
by defining
whenever
for some integers with
. Since
, we see from (5) (if
is small enough) that the equation (6) can only be true if
. As a consequence, we see that
is a equivalence relation. We can then form the quotient space
. Observe that if
are such that
,
, and
, then we also have
. Thus
has an addition operation
, defined on those equivalence classes
for which
for at least one representative
of
respectively. One easily verifies that this gives
the structure of a local group.
Now suppose for sake of contradiction that is isomorphic to a restriction of a global topological group
. Since
for all
, we thus have a map
which annihilates all of the
, and is locally additive in the sense that
whenever
. In particular, we see that all the elements of
commute with each other. Furthermore the kernel
is precisely equal to the set
As the span a dense subset of
, we can find integers
such that
and
We claim that lies in the kernel of
, contradicting the description (7) of that description (and the linear independence of the
). To see this, we observe for a sufficiently large natural number
that the local homomorphism property (and the commutativity) gives
and hence (by further application of local homomorphism and commutativity)
But by yet more application of the local homomorphism property,
and the claim follows.
Now we glue together the examples in Proposition 7 to establish Theorem 3. We work in the space , the elements of which we can think of as a sequence
of uniformly bounded functions
. The unit ball in this space can then be identified (as a set) with the product
, where
is the unit ball in
, though we caution that the topology on
is not given by the product topology (or the box topology).
We can combine the equivalence relations on
to a relation
on
, defined by setting
iff
for all
. This is clearly an equivalence relation on
, and so we can create the quotient space
with the quotient topology. One easily verifies that this gives a local group. The sets
form a neighbourhood base of the identity, but none of these sets is isomorphic (even as a discrete local group) to a subset of a global group, as it contains a copy of
, and the claim follows.

8 comments
Comments feed for this article
18 August, 2011 at 1:32 am
mikael
The restriction of a group to an open neighbourhood does not satisfy the first part of the (local closure) axiom in your definition of a local group. Perhaps this axiom should be that
of a group to an open neighbourhood does not satisfy the first part of the (local closure) axiom in your definition of a local group. Perhaps this axiom should be that  be a neigbourhood of
be a neigbourhood of  ?
?
18 August, 2011 at 7:26 am
Terence Tao
The first axiom is satisfied by because
because  contains a neighbourhood of
contains a neighbourhood of 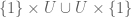 . (Note that the underlying set in the local group
. (Note that the underlying set in the local group  is
is  , not
, not  .)
.)
27 August, 2011 at 11:35 am
254A, Notes 0 – Hilbert’s fifth problem and related topics « What’s new
[…] which is isomorphic the image of the Heisenberg group under the Weil representation, or equivalently the group of isometries of generated by translations and modulations. Despite this, though, it is helpful to think of closed linear groups and Lie groups as being almost the same concept as a first approximation. For instance, one can show using Ado’s theorem that every Lie group is locally isomorphic to a linear local group (we will discuss local groups later in this course, and see also this post). […]
1 September, 2011 at 6:15 pm
254A, Notes 1: Lie groups, Lie algebras, and the Baker-Campbell-Hausdorff formula « What’s new
[…] up the barest bones of the theory of local groups here; a more detailed discussion may be found at this previous blog post. Definition 1 (Local group) A local topological group , or local group for short, is a topological […]
13 September, 2011 at 8:40 am
Allen Knutson
You should look into formal groups in characteristic $p$, i.e. group structures on Spec F_p[[x]]; I think you might appreciate (or even like!) them at this point.
Sample new concept: the additive group and multiplicative group give isomorphic formal group laws on Q[[x]], but not on F_p[[x]].
16 September, 2011 at 3:33 am
Example: Gromov-Hausdorff distances and the Heisenberg group, PART 2 | chorasimilarity
[…] the groups and are isomorphic. If you don’t know what a local group is then see the post Notes on local groups by Terence […]
28 September, 2011 at 2:56 pm
aaal2
I really eager to know how will your team to use these knowledge to solve sum-product problem.Looking forward new posts. licitatii
29 October, 2011 at 11:25 am
Associativity of the Baker-Campbell-Hausdorff formula « What’s new
[…] by using (3) to define a smooth local group structure on a neighbourhood of the identity. (See this previous post for a definition of a local Lie group.) The main difficulty in doing so is in verifying that the […]