In this set of notes, we describe the basic analytic structure theory of Lie groups, by relating them to the simpler concept of a Lie algebra. Roughly speaking, the Lie algebra encodes the “infinitesimal” structure of a Lie group, but is a simpler object, being a vector space rather than a nonlinear manifold. Nevertheless, thanks to the fundamental theorems of Lie, the Lie algebra can be used to reconstruct the Lie group (at a local level, at least), by means of the exponential map and the Baker-Campbell-Hausdorff formula. As such, the local theory of Lie groups is completely described (in principle, at least) by the theory of Lie algebras, which leads to a number of useful consequences, such as the following:
- (Local Lie implies Lie) A topological group
is Lie (i.e. it is isomorphic to a Lie group) if and only if it is locally Lie (i.e. the group operations are smooth near the origin).
- (Uniqueness of Lie structure) A topological group has at most one smooth structure on it that makes it Lie.
- (Weak regularity implies strong regularity, I) Lie groups are automatically real analytic. (In fact one only needs a “local
” regularity on the group structure to obtain real analyticity.)
- (Weak regularity implies strong regularity, II) A continuous homomorphism from one Lie group to another is automatically smooth (and real analytic).
The connection between Lie groups and Lie algebras also highlights the role of one-parameter subgroups of a topological group, which will play a central role in the solution of Hilbert’s fifth problem.
We note that there is also a very important algebraic structure theory of Lie groups and Lie algebras, in which the Lie algebra is split into solvable and semisimple components, with the latter being decomposed further into simple components, which can then be completely classified using Dynkin diagrams. This classification is of fundamental importance in many areas of mathematics (e.g. representation theory, arithmetic geometry, and group theory), and many of the deeper facts about Lie groups and Lie algebras are proven via this classification (although in such cases it can be of interest to also find alternate proofs that avoid the classification). However, it turns out that we will not need this theory in this course, and so we will not discuss it further here (though it can of course be found in any graduate text on Lie groups and Lie algebras).
— 1. Local groups —
The connection between Lie groups and Lie algebras will be local in nature – the only portion of the Lie group that will be of importance will be the portion that is close to the group identity . To formalise this locality, it is convenient to introduce the notion of a local group and a local Lie group, which are local versions of the concept of a topological group and a Lie group respectively. We will only set up the barest bones of the theory of local groups here; a more detailed discussion may be found at this previous blog post.
Definition 1 (Local group) A local topological group
, or local group for short, is a topological space
equipped with an identity element
, a partially defined but continuous multiplication operation
for some domain
, and a partially defined but continuous inversion operation
, where
, obeying the following axioms:
- (Local closure)
is an open neighbourhood of
, and
is an open neighbourhood of
.
- (Local associativity) If
are such that
and
are both well-defined in
, then they are equal. (Note however that it may be possible for one of these products to be defined but not the other.)
- (Identity) For all
,
.
- (Local inverse) If
and
is well-defined in
, then
. (In particular this, together with the other axioms, forces
.)
We will sometimes use additive notation for local groups if the groups are locally abelian (thus if
is defined, then
is also defined and equal to
.)
A local group is said to be symmetric if
, i.e. if every element
in
has an inverse
that is also in
.
A local Lie group is a local group that is also a smooth manifold, in such a fashion that the partially defined group operations
are smooth on their domain of definition.
Clearly, every topological group is a local group, and every Lie group is a local Lie group. We will sometimes refer to the former concepts as global topological groups and global Lie groups in order to distinguish them from their local counterparts. One could also consider local discrete groups, in which the topological structure is just the discrete topology, but we will not need to study such objects in this course.
A model class of examples of a local (Lie) group comes from restricting a global (Lie) group to an open neighbourhood of the identity. Let us formalise this concept:
Definition 2 (Restriction) If
is a local group, and
is an open neighbourhood of the identity in
, then we define the restriction
of
to
to be the topological space
with domains
and
, and with the group operations
being the restriction of the group operations of
to
,
respectively. If
is symmetric (in the sense that
is well-defined and lies in
for all
), then this restriction
will also be symmetric. If
is a global or local Lie group, then
will also be a local Lie group. We will sometimes abuse notation and refer to the local group
simply as
.
Thus, for instance, one can take the Euclidean space , and restrict it to a ball
centred at the origin, to obtain an additive local group
. In this group, two elements
in
have a well-defined sum
only when their sum in
stays inside
. Intuitively, this local group behaves like the global group
as long as one is close enough to the identity element
, but as one gets closer to the boundary of
, the group structure begins to break down.
It is natural to ask the question as to whether every local group arises as the restriction of a global group. The answer to this question is somewhat complicated, and can be summarised as “essentially yes in certain circumstances, but not in general”. See this previous blog post for more discussion.
A key example of a local Lie group for this blog post will come from pushing forward a Lie group via a coordinate chart near the origin:
Example 1 Let
be a global or local Lie group of some dimension
, and let
be a smooth coordinate chart from a neighbourhood
of the identity
in
to a neighbourhood
of the origin
in
, such that
maps
to
. Then we can define a local group
which is the set
(viewed as a smooth submanifold of
) with the local group identity
, the local group multiplication law
defined by the formula
defined whenever
are well-defined and lie in
, and the local group inversion law
defined by the formula
defined whenever
are well-defined and lie in
. One easily verifies that
is a local Lie group. We will sometimes denote this local Lie group as
, to distinguish it from the additive local Lie group
arising by restriction of
to
. The precise distinction between the two local Lie groups will in fact be a major focus of this post.
Example 2 Let
be the Lie group
, and let
be the ball
. If we then let
be the ball
and
be the map
, then
is a smooth coordinate chart (after identifying
with
), and by the construction in the preceding exercise,
becomes a local Lie group with the operations
(defined whenever
all lie in
) and
(defined whenever
and
both lie in
). Note that this Lie group structure is not equal to the additive structure
on
, nor is it equal to the multiplicative structure
on
given by matrix multiplication, which is one of the reasons why we use the symbol
instead of
or
for such structures.
Many (though not all) of the familiar constructions in group theory can be generalised to the local setting, though often with some slight additional subtleties. We will not systematically do so here, but we give a single such generalisation for now:
Definition 3 (Homomorphism) A continuous homomorphism
between two local groups
is a continuous map from
to
with the following properties:
maps the identity
of
to the identity
of
:
.
- If
is such that
is well-defined in
, then
is well-defined in
and is equal to
.
- If
are such that
is well-defined in
, then
is well-defined and equal to
.
A smooth homomorphism
between two local Lie groups
is a continuous homomorphism that is also smooth.
It is easy to see that the composition of two continuous homomorphisms is again a continuous homomorphism; this gives the class of local groups the structure of a category. Similarly, the class of local Lie groups with their smooth homomorphisms is also a category.
Note that homomorphisms on a local group are defined on the entirety of
; it is also natural to consider (continuous or smooth) local homomorphisms, which are only defined on an open neighbourhood of the identity in
, with two local homomorphisms considered equivalent if they agree on a (possibly smaller) open neighbourhood of the identity. We will not need to do so for now, however.
Example 3 With the notation of Example 1,
is a smooth homomorphism from the local Lie group
to the local Lie group
. In fact, it is a smooth isomorphism, since
provides the inverse homomorphism.
Let us say that a word in a local group
is well-defined in
(or well-defined, for short) if every possible way of associating this word using parentheses is well-defined from applying the product operation. For instance, in order for
to be well-defined,
,
,
,
, and
must all be well-defined. For instance, in the additive local group
(with the group structure restricted from that of the integers
),
is not well-defined because one of the ways of associating this sum, namely
, is not well-defined (even though
is well-defined).
Exercise 1 (Iterating the associative law)
- Show that if a word
in a local group
is well-defined, then all ways of associating this word give the same answer, and so we can uniquely evaluate
as an element in
.
- Give an example of a word
in a local group
which has two ways of being associated that are both well-defined, but give different answers. (Hint: the local associativity axiom prevents this from happening for
, so try
. A small discrete local group will already suffice to give a counterexample; verifying the local group axioms are easier if one makes the domain of definition of the group operations as small as one can get away with while still having the counterexample.)
— 2. Some differential geometry —
To define the Lie algebra of a Lie group, we must first quickly recall some basic notions from differential geometry associated to smooth manifolds (which are not necessarily embedded in some larger Euclidean space, but instead exist intrinsically as abstract geometric structures). This requires a certain amount of abstract formalism in order to define things rigorously, though for the purposes of visualisation, it is more intuitive to view these concepts from a more informal geometric perspective.
We begin with the concept of the tangent space and related structures.
Definition 4 (Tangent space) Let
be a smooth
-dimensional manifold. At every point
of this manifold, we can define the tangent space
of
at
. Formally, this tangent space can be defined as the space of all continuously differentiable curves
defined on an open interval
containing
with
, modulo the relation that two curves
are considered equivalent if they have the same derivative at
, in the sense that
where
is a coordinate chart of
defined in a neighbourhood of
; it is easy to see from the chain rule that this equivalence is independent of the actual choice of
. Using such a coordinate chart, one can identify the tangent space
with the Euclidean space
, by identifying
with
. One easily verifies that this gives
the structure of a
-dimensional vector space, in a manner which is independent of the choice of coordinate chart
. Elements of
are called tangent vectors of
at
. If
is a continuously differentiable curve with
, the equivalence class of
in
will be denoted
.
The space
of pairs
, where
is a point in
and
is a tangent vector of
at
, is called the tangent bundle.
If
is a smooth map between two manifolds, we define the derivative map
to be the map defined by setting
for all continously differentiable curves
with
for some
. We also write
for
, so that for each
,
is a map from
to
. One can easily verify that this latter map is linear. We observe the chain rule
for any smooth maps
,
. (Indeed, one can view the tangent operator
and the derivative operator
together as a single covariant functor from the category of smooth manifolds to itself, although we will not need to use this perspective here.)
Observe that if
is an open subset of
, then
may be identified with
. In particular, every coordinate chart
of
gives rise to a coordinate chart
of
, which gives
the structure of a smooth
-dimensional manifold.
Remark 1 Informally, one can think of a tangent vector
as an infinitesimal vector from the point
of
to a nearby point
on
, where
is infinitesimally small; a smooth map
then sends
to
. One can make this informal perspective rigorous by means of nonstandard analysis, but we will not do so here.
Once one has the notion of a tangent bundle, one can define the notion of a smooth vector field:
Definition 5 (Vector fields) A smooth vector field on
is a smooth map
which is a right inverse for the projection map
, thus (by slight abuse of notation)
maps
to
for some
. The space of all smooth vector fields is denoted
. It is clearly a real vector space. In fact, it is a
-module: given a smooth vector field
and a smooth function
(i.e. a smooth map
), one can define the product
in the obvious manner:
, and one easily verifies the module axioms.
Given a smooth function
and a smooth vector field
, we define the directional derivative
of
along
by the formula
whenever
is a continuously differentiable function with
and
; one easily verifies that
is well-defined and is an element of
.
Remark 2 One can define
in a more “co-ordinate free” manner as
where
is the projection map to the second coordinate of
; one can also view
as the Lie derivative of
along
(although, in most texts, the latter definition would be circular, because the Lie derivative is usually defined using the directional derivative).
Remark 3 If
is an open subset of
, a smooth vector field on
can be identified with a smooth map
from
to
. If
is a smooth vector field on
and
is a coordinate chart of
, then the pushforward
of
by
is a smooth vector field of
. Thus, in coordinates, one can view vector fields as maps from open subsets of
to
. This perspective is convenient for quick and dirty calculations; for instance, in coordinates, the directional derivative
is the same as the familiar directional derivative
from several variable calculus. If however one wishes to perform several changes of variable, then the more intrinsically geometric (and “coordinate-free”) perspective outlined above can be more helpful.
There is a fundamental link between smooth vector fields and derivations of :
Exercise 2 (Correspondence between smooth vector fields and derivations) Let
be a smooth manifold.
- If
is a smooth vector field, show that
is a derivation on the (real) algebra
, i.e. a (real) linear map that obeys the Leibniz rule
for all
.
- Conversely, if
is a derivation on
, show that there exists a unique smooth vector field
such that
.
We see from the above exercise that smooth vector fields can be interpreted as a purely algebraic construction associated to the real algebra , namely as the space of derivations on that vector space. This can be useful for analysing the algebraic structure of such vector fields. Indeed, we have the following basic algebraic observation:
Exercise 3 (Commutator of derivations is a derivation) Let
be two derivations on an algebra
. Show that the commutator
is also a derivation on
.
From the preceding two exercises, we can define the Lie bracket of two vector fields
by the formula
This gives the space of smooth vector fields the structure of an (infinite-dimensional) Lie algebra:
Definition 6 (Lie algebra) A (real) Lie algebra is a real vector space
(possibly infinite dimensional), together with a bilinear map
which is anti-symmetric (thus
for all
, or equivalently
for all
) and obeys the Jacobi identity
for all
.
Exercise 4 If
is a smooth manifold, show that
(equipped with the Lie bracket) is a Lie algebra.
— 3. The Lie algebra of a Lie group —
Let be a (global) Lie group. By definition,
is then a smooth manifolds, so we can thus define the tangent bundle
and smooth vector fields
as in the preceding section. In particular, we can define the tangent space
of
at the identity element
.
If , then the left multiplication operation
is, by definition of a Lie group, a smooth map from
to
. This creates a derivative map
from the tangent bundle
to itself. We say that a vector field
is left-invariant if one has
for all
, or equivalently if
for all
.
Exercise 5 Let
be a (global) Lie group.
- Show that for every element
of
there is a unique left-invariant vector field
such that
.
- Show that the commutator
of two left-invariant vector fields is again a left-invariant vector field.
From the above exercise, we can identify the tangent space with the left-invariant vector fields on
, and the Lie bracket structure on the latter then induces a Lie bracket (which we also call
) on
. The vector space
together with this Lie bracket is then a (finite-dimensional) Lie algebra, which we call the Lie algebra of the Lie group
, and we write as
.
Remark 4 Informally, an element
of the Lie algebra
is associated with an infinitesimal perturbation
of the identity in the Lie group
. This intuition can be formalised fairly easily in the case of matrix Lie groups such as
; for more abstract Lie groups, one can still formalise things using nonstandard analysis, but we will not do so here.
Exercise 6
- Show that the Lie algebra
of the general linear group
can be identified with the space
of
complex matrices, with the Lie bracket
.
- Describe the Lie algebra
of the unitary group
.
- Describe the Lie algebra
of the special unitary group
.
- Describe the Lie algebra
of the orthogonal
.
- Describe the Lie algebra
of the special orthogonal
.
- Describe the Lie algebra of the Heisenberg group
.
Exercise 7 Let
be a smooth homomorphism between (global) Lie groups. Show that the derivative map
at the identity element
is then a Lie algebra homomorphism from the Lie algebra
of
to the Lie algebra
of
(thus this map is linear and preserves the Lie bracket). (From this and the chain rule (1), we see that the map
creates a covariant functor from the category of Lie groups to the category of Lie algebras.)
We have seen that every global Lie group gives rise to a Lie algebra. One can also associate Lie algebras to local Lie groups as follows:
Exercise 8 Let
be a local Lie group. Let
be a symmetric neighbourhood of the identity in
. (It is not difficult to see that least one such neighbourhood exists.) Call a vector field
left-invariant if, for every
, one has
, where
is the left-multiplication map
, defined on the open set
(where we adopt the convention that
is shorthand for “
is well-defined and lies in
“).
Remark 5 In the converse direction, it is also true that every finite-dimensional Lie algebra can be associated to either a local or a global Lie group; this is known as Lie’s third theorem. However, this theorem is somewhat tricky to prove (particularly if one wants to associate the Lie algebra with a global Lie group), requiring the non-trivial algebraic tool of Ado’s theorem (discussed in this previous blog post); see Exercise 21 below.
— 4. The exponential map —
The exponential map on the reals
(or its extension to the complex numbers
) is of course fundamental to modern analysis. It can be defined in a variety of ways, such as the following:
- (i)
is the differentiable map obeying the ODE
and the initial condition
.
- (ii)
is the differentiable map obeying the homomorphism property
and the initial condition
.
- (iii)
is the limit of the functions
as
.
- (iv)
is the limit of the infinite series
.
We will need to generalise this map to arbitrary Lie algebras and Lie groups. In the case of matrix Lie groups (and matrix Lie algebras), one can use the matrix exponential, which can be defined efficiently by modifying definition (iv) above, and which was already discussed in the previous set of notes. It is however difficult to use this definition for abstract Lie algebras and Lie groups. The definition based on (ii) will ultimately be the best one to use for the purposes of this course, but for foundational purposes (i) or (iii) is initially easier to work with. In most of the foundational literature on Lie groups and Lie algebras, one uses (i), in which case the existence and basic properties of the exponential map can be provided by the Picard existence theorem from the theory of ordinary differential equations. However, we will use (iii), because it relies less heavily on the smooth structure of the Lie group, and will therefore be more aligned with the spirit of Hilbert’s fifth problem (which seeks to minimise the reliance of smoothness hypotheses whenever possible). Actually, for minor technical reasons it is slightly more convenient to work with the limit of rather than
.
We turn to the details. It will be convenient to work in local coordinates, and for applications to Hilbert’s fifth problem it will be useful to “forget” almost all of the smooth structure. We make the following definition:
Definition 7 (
local group) A
local group is a local group
that is an open neighbourhood of the origin
in a Euclidean space
, with group identity
, and whose group operation
obeys the estimate
for all sufficiently small
, where the implied constant in the
notation can depend on
but is uniform in
.
Example 4 Let
be a local Lie group of some dimension
, and let
be a smooth coordinate chart that maps a neighbourhood
of the group identity
to a neighbourhood
of the origin
in
, with
. Then, as explained in Example 1,
is a local Lie group with identity
; in particular, one has
From Taylor expansion (using the smoothness of
) we thus have (4) for sufficiently small
. Thus we see that every local Lie group generates a
local group when viewed in coordinates.
Remark 6 In real analysis, a (locally)
function is a function
on a domain
which is continuously differentiable (i.e. in the regularity class
), and whose first derivatives
are (locally) Lipschitz (i.e. in the regularity class
) the
regularity class is slightly weaker (i.e. larger) than the class
of twice continuously differentiable functions, but much stronger than the class
of singly continuously differentiable functions. See this previous blog post for more on these sorts of regularity classes. The reason for the terminology
in the above definition is that
regularity is essentially the minimal regularity for which one has the Taylor expansion
for any
in the domain of
, and any
sufficiently close to
; note that the asymptotic (4) is of this form.
We now estimate various expressions in a local group.
Exercise 9 Let
be a
local group. Throughout this exercise, the implied constants in the
notation can depend on
, but not on parameters such as
.
- (i) Show that there exists an
such that one has
whenever
and
are such that
, and the implied constant is uniform in
. Here and in the sequel we adopt the convention that a statement such as (5) is automatically false unless all expressions in that statement are well-defined. (Hint: induct on
using (4). It is best to replace the asymptotic
notation by explicit constants
in order to ensure that such constants remain uniform in
.) In particular, one has the crude estimate
under the same hypotheses as above.
- (ii) Show that one has
for
sufficiently close to the origin.
- (iii) Show that
for
sufficiently close to the origin. (Hint: first show that
, then express
as the product of
and
.)
- (iv) Show that
whenever
are sufficiently close to the origin.
- (v) Show that
whenever
are sufficiently close to the origin.
- (vi) Show that there exists an
such that
whenever
and
are such that
.
- (vii) Show that there exists an
such that
for all
and
such that
, where
is the product of
copies of
(assuming of course that this product is well-defined) for
, and
.
- (viii) Show that there exists an
such that
for all
and
such that
. (Hint: do the case when
is positive first. In that case, express
as the product of
conjugates of
by various powers of
.)
We can now define the exponential map on this
local group by defining
for any in a sufficiently small neighbourhood
of the origin in
.
Exercise 10 Let
be a local
group.
- (i) Show that if
is a sufficiently small neighbourhood of the origin in
, then the limit in (6) exists for all
. (Hint: use the previous exercise to estimate the distance between
and
.) Establish the additional estimate
- (ii) Show that if
is a smooth curve with
, and
is sufficiently small, then
- (iii) Show that for all sufficiently small
, one has the bilipschitz property
Conclude in particular that for
sufficiently small,
is a homeomorphism between
and an open neighbourhood
of the origin. (Hint: To show that
contains a neighbourhood of the origin, use (7) and the contraction mapping theorem.)
- Show that
for
and
with
sufficiently small. (Hint: first handle the case when
are dyadic numbers.)
- (iv) Show that for any sufficiently small
, one has
Then conclude the stronger estimate
- (v) Show that for any sufficiently small
, one has
(Hint: use the previous part, as well as (viii) of Exercise 9.)
Let us say that a local group is radially homogeneous if one has
whenever and
are such that
are sufficiently small. (In particular, this implies that
for sufficiently small
.) From the above exercise, we see that any
local group
can be made into a radially homogeneous
local group
by first restricting to an open neighbourhood
of the identity, and then applying the logarithmic homeomorphism
. Thus:
Corollary 8 Every
local group has a neighbourhood of the identity which is isomorphic (as a topological group) to a radially homogeneous
local group.
Now we study the exponential map on global Lie groups. If is a global Lie group, and
is its Lie algebra, we define the exponential map
on a global Lie group
by setting
whenever is a smooth curve with
.
Exercise 11 Let
be a global Lie group.
- (i) Show that the exponential map is well-defined. (Hint: First handle the case when
is small, using the previous exercise, then bootstrap to larger values of
.)
- (ii) Show that for all
and
, one has
and
(Hint: again, begin with the case when
are small.)
- (iii) Show that the exponential map is continuous.
- (iv) Show that for each
, the function
is the unique homomorphism from
to
that is differentiable at
with derivative equal to
.
Proposition 9 (Lie’s first theorem) Let
be a Lie group. Then the exponential map is smooth. Furthermore, there is an open neighbourhood
of the origin in
and an open neighbourhood
of the identity in
such that the exponential map
is a diffeomorphism from
to
.
Proof: We begin with the smoothness. From the homomorphism property we see that
for all and
. If
and
are sufficiently small, and one uses a coordinate chart
near the origin, the function
then satisfies an ODE of the form
for some smooth function , with initial condition
; thus by the fundamental theorem of calculus we have
Now let . An application of the contraction mapping theorem (in the function space
localised to small region of spacetime) then shows that
lies in
for small enough
, and by further iteration of the integral equation we then conclude that
is
times continuously differentiable for small enough
. By (8) we then conclude that
is smooth everywhere.
Since
we see that the derivative of the exponential map at the origin is the identity map on . The second claim of the proposition thus follows from the inverse function theorem.
In view of this proposition, we see that given a vector space basis for the Lie algebra
, we may obtain a smooth coordinate chart
for some neighbourhood
of the identity and neighbourhood
of the origin in
by defining
for sufficiently small . These are known as exponential coordinates of the first kind. Although we will not use them much here, we also note that there are exponential coordinates of the second kind, in which the expression
is replaced by the slight variant
.
Using exponential coordinates of the first kind, we see that we may identify a local piece of the Lie group
with the radially homogeneous
local group
. In the next section, we will analyse such radially homogeneous
groups further. For now, let us record some easy consequences of the existence of exponential coordinates. Define a one-parameter subgroup of a topological group
to be a continuous homomorphism
from
to
.
Exercise 12 (Classification of one-parameter subgroups) Let
be a Lie group. For any
, show that the map
is a one-parameter subgroup. Conversely, if
is a one-parameter subgroup, there exists a unique
such that
for all
. (Hint: mimic the proof of Proposition 1 of Notes 0.)
Proposition 10 (Weak regularity implies strong regularity) Let
be global Lie groups, and let
be a continuous homomorphism. Then
is smooth.
Proof: Since is a continuous homomorphism, it maps one-parameter subgroups of
to one-parameter subgroups of
. Thus, for every
, there exists a unique element
such that
for all . In particular, we see that
is homogeneous:
for all
and
. Next, we observe using (9) and the fact that
is a continuous homomorphism that for any
and
, one has
and thus is additive:
We conclude that is a linear transformation from the finite-dimensional vector space
to the finite-dimensional vector space
. In particular,
is smooth. On the other hand, we have
Since and
are diffeomorphisms near the origin, we conclude that
is smooth in a neighbourhood of the identity. Using the homomorphism property (and the fact that the group operations are smooth for both
and
) we conclude that
is smooth everywhere, as required.
This fact has a pleasant corollary:
Corollary 11 (Uniqueness of Lie structure) Any (global) topological group can be made into a Lie group in at most one manner. More precisely, given a topological group
, there is at most one smooth structure one can place on
that makes the group operations smooth.
Proof: Suppose for sake of contradiction that one could find two different smooth structures on that make the group operations smooth, leading to two different Lie groups
based on
. The identity map from
to
is a continuous homomorphism, and hence smooth by the preceding proposition; similarly for the inverse map from
to
. This implies that the smooth structures coincide, and the claim follows.
Note that a general high-dimensional topological manifold may have more than one smooth structure, which may even be non-diffeomorphic to each other (as the example of exotic spheres demonstrates), so this corollary is not entirely vacuous.
Exercise 13 Let
be a connected (global) Lie group, let
be another (global) Lie group, and let
be a continuous homomorphism (which is thus smooth by Proposition 10). Show that
is uniquely determined by the derivative map
. In other words, if
is another continuous homomorphism with
, then
. (Hint: first prove this in a small neighbourhood of the origin. What group does this neighbourhood generate?) What happens if
is not connected?
Exercise 14 (Weak regularity implies strong regularity, local version) Let
be local Lie groups, and let
be a continuous homomorphism. Show that
is smooth in a neighbourhood of the identity in
.
Exercise 15 (Local Lie implies Lie) Let
be a global topological group. Suppose that there is an open neighbourhood
of the identity such that the local group
can be given the structure of a local Lie group. Show that
can be given the structure of a global Lie group. (Hint: We already have at least one coordinate chart on
; translate it around to create an atlas of such charts. To show compatibility of the charts and global smoothness of the group, one needs to show that the conjugation maps
are smooth near the origin for any
. To prove this, use Exercise 14.)
— 5. The Baker-Campbell-Hausdorff formula —
We now study radially homogeneous local groups in more detail. We will show
Theorem 12 (Baker-Campbell-Hausdorff formula, qualitative version) Let
be a radially homogeneous
local group. Then the group operation
is real analytic near the origin. In particular, after restricting
to a sufficiently small neighbourhood of the origin, one obtains a local Lie group.
We will in fact give a more precise formula for , known as the Baker-Campbell-Haudorff-Dynkin formula, in the course of proving Theorem 12.
Remark 7 In the case where
comes from viewing a general linear group
in local exponential coordinates, the group operation
is given by
for sufficiently small
. Thus, a corollary of Theorem 12 is that this map is real analytic.
We begin the proof of Theorem 12. Throughout this section, is a fixed radially homogeneous
local group. We will need some variants of the basic bound (4).
Exercise 16 (Lipschitz bounds) If
are sufficiently small, establish the bounds
(Hint: to prove (15), start with the identity
.)
Now we exploit the radial homogeneity to describe the conjugation operation as a linear map:
Lemma 13 (Adjoint representation) For all
sufficiently close to the origin, there exists a linear transformation
such that
for all
sufficiently close to the origin.
Remark 8 Using the matrix example from Remark 7, we are asserting here that
for some linear transform
of
, and all sufficiently small
. Indeed, using the basic matrix identity
for invertible
(coming from the fact that the conjugation map
is a continuous ring homomorphism) we see that we may take
here.
Proof: Fix . The map
is continuous near the origin, so it will suffice to establish additivity, in the sense that
for sufficiently close to the origin.
Let be a large natural number. Then from (11) we have
Conjugating this by , we see that
But from (4) we have
and thus (by Exercise 16)
But if we split as the product of
and
and use (4), we have
Putting all this together we see that
sending we obtain the claim.
From (4) we see that
for sufficiently small. Also from the associativity property we see that
for all sufficiently small. Combining these two properties (and using (15)) we conclude in particular that
for sufficiently small. Thus we see that
is a (locally) continuous linear representation. In particular,
is a (locally) continuous homomorphism into a linear group, and so (by Proposition 1 of Notes 0) we have the Hadamard lemma
for all sufficiently small , where
is the linear transformation
From (21), (20), (4) we see that
for sufficiently small, and so by the product rule we have
Also we clearly have for
small. Thus we see that
is linear in
, and so we have
for some bilinear form .
One can show that this bilinear form in fact defines a Lie bracket (i.e. it is anti-symmetric and obeys the Jacobi identity), but for now, all we need is that it is manifestly real analytic (since all bilinear forms are polynomial and thus analytic). In particular and
depend analytically on
.
We now give an important approximation to in the case when
is small:
Lemma 14 For
sufficiently small, we have
where
Proof: If we write , then
(by (4)) and
We will shortly establish the approximation
inverting
we obtain the claim.
It remains to verify (22). Let be a large natural number. We can expand the left-hand side of (22) as a telescoping series
Using (11), the first summand can be expanded as
From (15) one has , so by (17), (18) we can write the preceding expression as
which by definition of can be rewritten as
From (15) one has
while from (20) one has , hence from (4) we can rewrite (24) as
Inserting this back into (23), we can thus write the left-hand side of (22) as
Writing , and then letting
, we conclude (from the convergence of the Riemann sum to the Riemann integral) that
and the claim follows.
Remark 9 In the matrix case, the key computation is to show that
To see this, we can use the fundamental theorem of calculus to write the left-hand side as
Since
and
, we can rewrite this as
Since
, this becomes
since
, we obtain the desired claim.
We can integrate the above formula to obtain an exact formula for :
Corollary 15 (Baker-Campbell-Hausdorff-Dynkin formula) For
sufficiently small, one has
The right-hand side is clearly real analytic in and
, and Theorem 12 follows.
Proof: Let be a large natural number. We can express
as the telescoping sum
From (11) followed by Lemma 14 and (21), one has
We conclude that
Sending , so that the Riemann sum converges to a Riemann integral, we obtain the claim.
Exercise 17 Use the Taylor-type expansion
to obtain the explicit expansion
where
, and show that the series is absolutely convergent for
small enough. Invert this to obtain the alternate expansion
Exercise 18 Let
be a radially homogeneous
local group. By Theorem 12, an open neighbourhood of the origin in
has the structure of a local Lie group, and thus by Exercise 8 is associated to a Lie algebra. Show that this Lie algebra is isomorphic to
and the Lie bracket
is given by (21). Note that this establishes a posteriori the fact that the bracket
occurring in (21) is anti-symmetric and obeys the Jacobi identity.
We now record some consequences of the Baker-Campbell-Hausdorff formula.
Exercise 19 (Lie groups are analytic) Let
be a global Lie group. Show that
is a real analytic manifold (i.e. one can find an atlas of smooth coordinate charts whose transition maps are all real analytic), and that the group operations are also real analytic (i.e. they are real analytic when viewed in the above-mentioned coordinate charts). Furthermore, show that any continuous homomorphism between Lie groups is also real analytic.
Exercise 20 (Lie’s second theorem) Let
be global Lie groups, and let
be a Lie algebra homomorphism. Show that there exists an open neighbourhood
of the identity in
and a homomorphism
from the local Lie group
to
such that
. If
is connected and simply connected, show that one can take
to be all of
.
Exercise 21 (Lie’s third theorem) Ado’s theorem asserts that every finite-dimensional Lie algebra is isomorphic to a subalgebra of
for some
. This (somewhat difficult) theorem and its proof is discussed in this previous blog post. Assuming Ado’s theorem as a “black box”, conclude the following claims:
- (i) (Lie’s third theorem, local version) Every finite-dimensional Lie algebra is isomorphic to the Lie algebra of some local Lie group.
- (ii) Every local or global Lie group has a neighbourhood of the identity that is isomorphic to a local linear Lie group (i.e. a local Lie group contained in
or
for some
).
- (iii) (Lie’s third theorem, global version) Every finite-dimensional Lie algebra
is isomorphic to the Lie algebra of some global Lie group. (Hint: from (i) and (ii), one may identify
with the Lie algebra of a local linear Lie group. Now consider the space of all smooth curves in the ambient linear group that are everywhere “tangent” to this local linear Lie group modulo “homotopy”, and use this to build the global Lie group.)
- (iv) (Lie’s third theorem, simply connected version) Every finite-dimensional Lie algebra
is isomorphic to the Lie algebra of some global connected, simply connected Lie group. Furthermore, this Lie group is unique up to isomorphism.
- (v) Show that every local Lie group
has a neighbourhood of the identity that is isomorphic to a neighbourhood of the identity of a global connected, simply connected Lie group. Furthermore, this Lie group is unique up to isomorphism.
Remark 10 One does not need the full strength of Ado’s theorem to establish conclusion (i) of the above exercise. Indeed, it suffices to show that the operation
defined in Exercise 17 is associative near the origin. To do this, it suffices to verify associativity in the sense of formal power series; and then by abstract nonsense one can lift up to the free Lie algebra on
generators, and then down to the free nilpotent Lie algebra on
generators and of some arbitrary finite step
, which one can verify to be a finite dimensional Lie algebra. Applying Ado’s theorem for the special case of nilpotent Lie algebras (which is easier to establish than the general case of Ado’s theorem, as discussed in this previous blog post), one can identify this nilpotent Lie algebra with a subalgebra of
for some
, and then one can argue as in the above exercise to conclude. However, I do not know how to establish conclusions (ii), (iii) or (iv) without using Ado’s theorem in full generality (and (ii) is in fact equivalent to this theorem, at least in characteristic
).
Remark 11 Lie’s three theorems can be interpreted as establishing an equivalence between three different categories: the category of finite-dimensional Lie algebras; the category of local Lie groups (or more precisely, the category of local Lie group germs, formed by identifying local Lie groups that are identical near the origin); and the category of global connected, simply connected Lie groups. See this blog post for further discussion.
The fact that we were able to establish the Baker-Campbell-Hausdorff formula at the regularity level will be useful for the purposes of proving results related to Hilbert’s fifth problem. In particular, we have the following criterion for a group to be Lie (very much in accordance with the “weak regularity implies strong regularity for group-like objects” principle):
Lemma 16 (Criterion for Lie structure) Let
be a topological group. Show that
is Lie if and only if there is a neighbourhood of the identity in
which is isomorphic (as a topological group) to a
local group.
Proof: The “only if” direction is trivial. For the “if” direction, combine Corollary 8 with Theorem 12 and Exercise 15.
Remark 12 Informally, Lemma 16 asserts that
regularity can automatically be upgraded to smooth (
) or even real analytic (
) regularity for topological groups. In contrast, note that a locally Euclidean group has neighbourhoods of the identity that are isomorphic to a “
local group” (which is the same concept as a
local group, but without the asymptotic (4)). Thus we have reduced Hilbert’s fifth problem to the task of boosting
regularity to
regularity, rather than that of boosting
regularity to
regularity.
Exercise 22 Let
be a Lie group with Lie algebra
. For any
, show that

33 comments
Comments feed for this article
2 September, 2011 at 3:56 am
Combinatorics versus geometric… | chorasimilarity
[…] of using knowledge concerning topological groups in order to study discrete approximate groups, as Tao proposes in his new course, it is about discrete finitely generated groups with polynomial growth which, as Gromov taught us, […]
2 September, 2011 at 4:31 am
tanaka
Thank you for your good post.
By the way ,In Remark2, where does “Y” comes from?
[Oops, that was meant to be an X. Corrected, thanks – T.]
2 September, 2011 at 6:50 pm
254A, Notes 1: Lie groups, Lie algebras, and the Baker-Campbell-Hausdorff formula (via What's new) « Human Mathematics
[…] 254A, Notes 1: Lie groups, Lie algebras, and the Baker-Campbell-Hausdorff formula (via What's new) By human mathematics In this set of notes, we describe the basic analytic structure theory of Lie groups, by relating them to the simpler concept of a Lie algebra. Roughly speaking, the Lie algebra encodes the “infinitesimal” structure of a Lie group, but is a simpler object, being a vector space rather than a nonlinear manifold. Nevertheless, thanks to the fundamental theorems of Lie, the Lie algebra can be used to reconstruct the Lie group (at a local l … Read More […]
3 September, 2011 at 5:51 am
David Speyer
Typo: In the sentence beginning “However, we will use (iv)”, I imagine you mean (iii). [Corrected, thanks – T.]
5 September, 2011 at 2:45 pm
E. Mehmet Kiral
The fifth bullet point in exercise 6 seems to have a typo, $\mathbb{R}$ versus $\mathbb{C}$.
5 September, 2011 at 3:24 pm
Erik
It looks like you should have “..are well defined and lie in ” and
” and  instead of
instead of  in example 1. [Corrected, thanks, although
in example 1. [Corrected, thanks, although  is actually not a typo. -T.]
is actually not a typo. -T.]
7 September, 2011 at 5:01 am
Weekly Picks « Mathblogging.org — the Blog
[…] compactness theorem, n-Category Café on Hadwiger’s theorem, Terry Tao starting a series of posts on Hilbert’s fifth problem, and Vismath (in German, translation) and 0xDE on tilings. Also […]
8 September, 2011 at 2:10 pm
254A, Notes 2: Building Lie structure from representations and metrics « What’s new
[…] one-parameter subgroups to convert from the nonlinear setting to the linear setting. Recall from the previous notes that in a Lie group , the one-parameter subgroups are in one-to-one correspondence with the Lie […]
18 September, 2011 at 4:00 am
pavel zorin
Dear Prof. Tao,
I have some trouble with Exercise 9(v). Even in the easiest situation, that of Exercise 16(17), I keep getting terms like instead of |y-z| in the estimates. With the radial homogeneity assumption the two are equal, but otherwise there remains an error of O(|z|)². What can be done about it?
instead of |y-z| in the estimates. With the radial homogeneity assumption the two are equal, but otherwise there remains an error of O(|z|)². What can be done about it?
best regards,
pavel
18 September, 2011 at 9:23 am
Terence Tao
Ah yes, this requires an estimate which wasn’t explicitly in the previous exercises but which I’ve now added as Exercise 9(viii) (note that there has been some renumbering of exercises).
20 September, 2011 at 12:42 pm
pavel zorin
Thank you, this has helped me to show the Lipschitzianity of left and right translation, and thus Ex. 9 (vi) and (viii). I am however still lost with (vii), the asymptotics for .
.
What I think I can show is that it is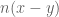 up to an arbitrarily small relative error, if
up to an arbitrarily small relative error, if  is small enough (from the analogous result
is small enough (from the analogous result  up to a small relative error). Unfortunately, this is much weaker then the error being
up to a small relative error). Unfortunately, this is much weaker then the error being  .
.
best regards,
pavel
20 September, 2011 at 1:47 pm
Terence Tao
Oops, that bound is indeed too strong to be true in general. I’ve replaced it with the bilipschitz bound as you indicated (which is what is actually needed going forward in the argument.)
31 March, 2013 at 3:28 am
THLee
I am looking for proofs for equivalence of any decomposition of a general anti-hermitain matrix when canonical coordinates of the first kind is mapped to the second kind in exponential map of SU(N) group. Can anyone suggest me any textbook or reference for this question?
20 September, 2011 at 5:18 pm
Erik
I’m having trouble understanding the term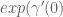 in exercise 10 (ii). I think this means the exponential map of a member of the equivalence class
in exercise 10 (ii). I think this means the exponential map of a member of the equivalence class  – in other words, a curve
– in other words, a curve  in
in  . But then this can’t be equal to the limit on the right since
. But then this can’t be equal to the limit on the right since  is (somewhat) arbitrary. Also, what does it mean to say that
is (somewhat) arbitrary. Also, what does it mean to say that  is sufficiently small.
is sufficiently small.
20 September, 2011 at 6:25 pm
Terence Tao
Note that while there are multiple curves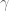 with the same derivative
with the same derivative  at zero, it will turn out that each of these curves ends up with the same limiting value of
at zero, it will turn out that each of these curves ends up with the same limiting value of  , thus the apparent ambiguity of
, thus the apparent ambiguity of 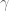 will disappear in the limit.
will disappear in the limit.
In any event, in a local group, G is a subset of a Euclidean space, so one can use the Euclidean definition of
group, G is a subset of a Euclidean space, so one can use the Euclidean definition of  in this case if one wishes.
in this case if one wishes.
20 September, 2011 at 7:28 pm
Erik
Thank you
27 September, 2011 at 3:29 pm
254A, Notes 3: Haar measure and the Peter-Weyl theorem « What’s new
[…] the last few notes, we have been steadily reducing the amount of regularity needed on a topological group in […]
8 October, 2011 at 11:11 am
Anonymous
Professor Tao,
In exercise 14, should G and H be local Lie groups?
[Corrected, thanks – T.]
8 October, 2011 at 9:53 pm
alingalatan
At the beginning of the proof of Proposition 9, shouldn’t it be , and not just $\rho_{\exp(tx)}^{left} x$?
, and not just $\rho_{\exp(tx)}^{left} x$?
[Corrected, thanks – T.]
28 October, 2011 at 1:35 am
Bruce Bartlett
I think that another way of integrating a Lie algebra to a Lie group (this is in regard to Remark 5), which doesn’t proceed via Ado’s theorem, is to define the group elements as equivalence classes of paths in the Lie algebra. My understanding is that there are two different equivalence relations one can put on the paths: the first can be found in the book “Lie Groups” by Duistermaat and Kolk, and the second can be found in Segal’s section of the book “Lectures on Lie Groups and Lie Algebras” by Carter, Segal and Macdonald. Both of these give rise to the same group I believe.
28 October, 2011 at 10:15 am
Terence Tao
I took a look at Carter-Segal-Macdonald (our library doesn’t have Duistermaat-Kolk). Unfortunately they omit the most crucial step of the argument, namely to show that two short paths are equivalent whenever they integrate out (via the infinitesimal form of BCH, i.e. Lemma 14 above) to the same element of the Lie algebra; they prove it using Ado’s theorem, but don’t indicate how to do it without that theorem (other than to say that it is “difficult”). So I suspect that the difficulty is simply being moved elsewhere.
29 October, 2011 at 11:25 am
Associativity of the Baker-Campbell-Hausdorff formula « What’s new
[…] for instance these notes of mine for a proof of this formula (it is for , but one easily obtains a similar proof for […]
5 March, 2012 at 10:43 pm
Johnny
I think ready solutions makes it easier.
I use Differential Geometry Library:
http://digi-area.com/DifferentialGeometryLibrary/
5 May, 2012 at 1:06 pm
alabair
I think there’s a typo in the definition 4 of the tangent space.
M instead of G.
7 October, 2012 at 6:56 pm
Some notes on Weyl quantisation « What’s new
[…] as well as exponential coordinates (of the first kind) on Lie groups, discussed for instance in this previous blog post. In contrast, the Kohn-Nirenberg quantisation […]
27 April, 2013 at 9:25 pm
Notes on the classification of complex Lie algebras | What's new
[…] counterparts in the category of Lie algebras (often with exactly the same terminology). See this previous blog post for more discussion about the connection between Lie algebras and Lie groups (that post was focused […]
5 September, 2013 at 9:23 pm
Notes on simple groups of Lie type | What's new
[…] (This statement can be made more precise using the Baker-Campbell-Hausdorff formula, discussed in this previous post.) On the other hand, every connected Lie group has a universal cover with the same Lie algebra […]
8 March, 2015 at 9:46 pm
Hao Zhuang
Reblogged this on Exponentials.
9 March, 2015 at 12:21 am
Anonymous
In definition 4, it seems that the (undefined) (appearing in line 4 and several other places) should be
(appearing in line 4 and several other places) should be  .
.
[Corrected, thanks – T.]
22 May, 2017 at 5:55 pm
Quantitative continuity estimates | What's new
[…] We remark that further manipulation of (iv) of the above exercise using the fundamental theorem of calculus eventually leads to the Baker-Campbell-Hausdorff-Dynkin formula, as discussed in this previous blog post. […]
20 April, 2019 at 12:28 pm
Arturo Rodríguez Fanlo
Dear Prof. Tao,
Thank you very much. If it is possible, I would sincerely appreciate any hint to show the lower bound of point (vii) of exercise 9:
In a local group, there is
local group, there is 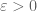 such that for any natural number
such that for any natural number  and any
and any  with
with 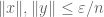
Again, thank you very much for everything.
Best wishes,
Arturo
20 April, 2019 at 3:15 pm
Terence Tao
Can you do the case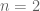 ? You may find it helpful to write
? You may find it helpful to write  and try to estimate both
and try to estimate both 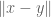 and
and 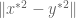 in terms of
in terms of  .
.
29 April, 2019 at 10:27 am
Arturo Rodriguez Fanlo
Dear Prof. Tao,
Thank you very much for your attention.
Best wishes,
Arturo