Given a function between two sets
, we can form the graph
which is a subset of the Cartesian product .
There are a number of “closed graph theorems” in mathematics which relate the regularity properties of the function with the closure properties of the graph
, assuming some “completeness” properties of the domain
and range
. The most famous of these is the closed graph theorem from functional analysis, which I phrase as follows:
Theorem 1 (Closed graph theorem (functional analysis)) Let
be complete normed vector spaces over the reals (i.e. Banach spaces). Then a function
is a continuous linear transformation if and only if the graph
is both linearly closed (i.e. it is a linear subspace of
) and topologically closed (i.e. closed in the product topology of
).
I like to think of this theorem as linking together qualitative and quantitative notions of regularity preservation properties of an operator ; see this blog post for further discussion.
The theorem is equivalent to the assertion that any continuous linear bijection from one Banach space to another is necessarily an isomorphism in the sense that the inverse map is also continuous and linear. Indeed, to see that this claim implies the closed graph theorem, one applies it to the projection from
to
, which is a continuous linear bijection; conversely, to deduce this claim from the closed graph theorem, observe that the graph of the inverse
is the reflection of the graph of
. As such, the closed graph theorem is a corollary of the open mapping theorem, which asserts that any continuous linear surjection from one Banach space to another is open. (Conversely, one can deduce the open mapping theorem from the closed graph theorem by quotienting out the kernel of the continuous surjection to get a bijection.)
It turns out that there is a closed graph theorem (or equivalent reformulations of that theorem, such as an assertion that bijective morphisms between sufficiently “complete” objects are necessarily isomorphisms, or as an open mapping theorem) in many other categories in mathematics as well. Here are some easy ones:
Theorem 2 (Closed graph theorem (linear algebra)) Let
be vector spaces over a field
. Then a function
is a linear transformation if and only if the graph
is linearly closed.
Theorem 3 (Closed graph theorem (group theory)) Let
be groups. Then a function
is a group homomorphism if and only if the graph
is closed under the group operations (i.e. it is a subgroup of
).
Theorem 4 (Closed graph theorem (order theory)) Let
be totally ordered sets. Then a function
is monotone increasing if and only if the graph
is totally ordered (using the product order on
).
Remark 1 Similar results to the above three theorems (with similarly easy proofs) hold for other algebraic structures, such as rings (using the usual product of rings), modules, algebras, or Lie algebras, groupoids, or even categories (a map between categories is a functor iff its graph is again a category). (ADDED IN VIEW OF COMMENTS: further examples include affine spaces and
-sets (sets with an action of a given group
).) There are also various approximate versions of this theorem that are useful in arithmetic combinatorics, that relate the property of a map
being an “approximate homomorphism” in some sense with its graph being an “approximate group” in some sense. This is particularly useful for this subfield of mathematics because there are currently more theorems about approximate groups than about approximate homomorphisms, so that one can profitably use closed graph theorems to transfer results about the former to results about the latter.
A slightly more sophisticated result in the same vein:
Theorem 5 (Closed graph theorem (point set topology)) Let
be compact Hausdorff spaces. Then a function
is continuous if and only if the graph
is topologically closed.
Indeed, the “only if” direction is easy, while for the “if” direction, note that if is a closed subset of
, then it is compact Hausdorff, and the projection map from
to
is then a bijective continuous map between compact Hausdorff spaces, which is then closed, thus open, and hence a homeomorphism, giving the claim.
Note that the compactness hypothesis is necessary: for instance, the function defined by
for
and
for
is a function which has a closed graph, but is discontinuous.
A similar result (but relying on a much deeper theorem) is available in algebraic geometry, as I learned after asking this MathOverflow question:
Theorem 6 (Closed graph theorem (algebraic geometry)) Let
be normal projective varieties over an algebraically closed field
of characteristic zero. Then a function
is a regular map if and only if the graph
is Zariski-closed.
Proof: (Sketch) For the only if direction, note that the map is a regular map from the projective variety
to the projective variety
and is thus a projective morphism, hence is proper. In particular, the image
of
under this map is Zariski-closed.
Conversely, if is Zariski-closed, then it is also a projective variety, and the projection
is a projective morphism from
to
, which is clearly quasi-finite; by the characteristic zero hypothesis, it is also separated. Applying (Grothendieck’s form of) Zariski’s main theorem, this projection is the composition of an open immersion and a finite map. As projective varieties are complete, the open immersion is an isomorphism, and so the projection from
to
is finite. Being injective and separable, the degree of this finite map must be one, and hence
and
are isomorphic, hence (by normality of
)
is contained in (the image of)
, which makes the map from
to
regular, which makes
regular.
The counterexample of the map given by
for
and
demonstrates why the projective hypothesis is necessary. The necessity of the normality condition (or more precisely, a weak normality condition) is demonstrated by (the projective version of) the map
from the cusipdal curve
to
. (If one restricts attention to smooth varieties, though, normality becomes automatic.) The necessity of characteristic zero is demonstrated by (the projective version of) the inverse of the Frobenius map
on a field
of characteristic
.
There are also a number of closed graph theorems for topological groups, of which the following is typical (see Exercise 3 of these previous blog notes):
Theorem 7 (Closed graph theorem (topological group theory)) Let
be
-compact, locally compact Hausdorff groups. Then a function
is a continuous homomorphism if and only if the graph
is both group-theoretically closed and topologically closed.
The hypotheses of being -compact, locally compact, and Hausdorff can be relaxed somewhat, but I doubt that they can be eliminated entirely (though I do not have a ready counterexample for this).
In several complex variables, it is a classical theorem (see e.g. Lemma 4 of this blog post) that a holomorphic function from a domain in to
is locally injective if and only if it is a local diffeomorphism (i.e. its derivative is everywhere non-singular). This leads to a closed graph theorem for complex manifolds:
Theorem 8 (Closed graph theorem (complex manifolds)) Let
be complex manifolds. Then a function
is holomorphic if and only if the graph
is a complex manifold (using the complex structure inherited from
) of the same dimension as
.
Indeed, one applies the previous observation to the projection from to
. The dimension requirement is needed, as can be seen from the example of the map
defined by
for
and
.
(ADDED LATER:) There is a real analogue to the above theorem:
Theorem 9 (Closed graph theorem (real manifolds)) Let
be real manifolds. Then a function
is continuous if and only if the graph
is a real manifold of the same dimension as
.
This theorem can be proven by applying invariance of domain (discussed in this previous post) to the projection of to
, to show that it is open if
has the same dimension as
.
Note though that the analogous claim for smooth real manifolds fails: the function defined by
has a smooth graph, but is not itself smooth.
(ADDED YET LATER:) Here is an easy closed graph theorem in the symplectic category:
Theorem 10 (Closed graph theorem (symplectic geometry)) Let
and
be smooth symplectic manifolds of the same dimension. Then a smooth map
is a symplectic morphism (i.e.
) if and only if the graph
is a Lagrangian submanifold of
with the symplectic form
.
In view of the symplectic rigidity phenomenon, it is likely that the smoothness hypotheses on can be relaxed substantially, but I will not try to formulate such a result here.
There are presumably many further examples of closed graph theorems (or closely related theorems, such as criteria for inverting a morphism, or open mapping type theorems) throughout mathematics; I would be interested to know of further examples.

27 comments
Comments feed for this article
20 November, 2012 at 7:08 pm
The closed graph theorem in various categories « Guzman's Mathematics Weblog
[…] The closed graph theorem in various categories. […]
20 November, 2012 at 7:12 pm
Jack
I remember that in one of Thurston’s papers that you mentioned before (I don’t remember the specific title), he listed several (coincidentally 8?) ways of thinking about the derivative (which happens to be discussed in Gowers’s new post today) when he illustrated how people understand mathematics. Can the philosophy of understanding a theorem in different categories here be regarded as kind of the same as that of understanding a concept in Thurston’s paper?
20 November, 2012 at 8:17 pm
Terence Tao
I think it’s more of a dual relationship. Thurston talks about using multiple fields of mathematics to gain a better understanding of a single concept. The discussion here is more like using a single concept (or more precisely, a single class of results) to try to gain a better understanding of multiple fields of mathematics.
20 November, 2012 at 7:37 pm
Allen Knutson
In Theorem 6, do you care that Y is normal? It seems like you only use that X is.
20 November, 2012 at 7:49 pm
Terence Tao
I think you’re right. In general, the properties of the codomain Y seem to be less important than the properties of the domain X for these theorems (which makes sense, since one is free to enlarge Y at will without really changing anything, whereas one cannot enlarge X at will). For instance, in Theorem 4, Y does not actually need to be totally ordered; in Theorem 3, Y can be a local group (or even a local magma) rather than a global one; and so forth.
6 November, 2015 at 9:47 am
John Gowers
The opposite is true in the topological case. Here, one direction (continuous implies closed graph) holds whenever is a Hausdorff space, while the other direction (closed graph implies continuous) holds whenever
is a Hausdorff space, while the other direction (closed graph implies continuous) holds whenever  is compact. There are no conditions on
is compact. There are no conditions on  .
.
6 November, 2015 at 9:49 am
John Gowers
In fact, we can characterize compact spaces an Hausdorff spaces in this way.
21 November, 2012 at 12:12 am
Anonymous
So the obvious question, is there a categorical version of the theorem, so that all the specializations fall out as corollaries?
21 November, 2012 at 9:11 am
Terence Tao
Looking at the engines that power these theorems, I would be very surprised if the Baire category theorem, Zariski’s main theorem, and invariance of domain could be deduced from a common universal result. (Also, while the same sort of counterexamples show up in many different contexts, such as the “1/x if x is nonzero and 0 if x is zero” function, or roots , it seems that very different hypotheses are needed to eliminate these potential counterexamples in different cases, and it does not look like they are easily tied together under a single category-theoretic framework.) But I think what might be realistic is to have a common category-theoretic description of what a closed graph theorem is, and how it is equivalent to other related results (such as open mapping theorems, or invertibility criteria for morphisms).
, it seems that very different hypotheses are needed to eliminate these potential counterexamples in different cases, and it does not look like they are easily tied together under a single category-theoretic framework.) But I think what might be realistic is to have a common category-theoretic description of what a closed graph theorem is, and how it is equivalent to other related results (such as open mapping theorems, or invertibility criteria for morphisms).
21 November, 2012 at 1:12 am
mircea petrache
A basic principle underlying some of the examples is that if a group G acts on spaces X,Y then f is is equivariant provided g acts on the graph by diagonal action. (This is purely formal: G being a group is unnecessary. It basically suffices that gx, gy have a fixed meaning for g in G, x in X, y in Y.) In general, it seems that the presence of a Closed Graph Theorem is a sign that in the given category morphisms and products are defined so that they fit well together.
[G-sets are a good example, and certainly linked to many of the other “algebraic” examples given; I’ve added them to the list. -T.]
21 November, 2012 at 3:17 am
Tim Sullivan
It seems that there’s a lot of switching back and forth between “f” and “T” throughout the post, even within the same sentence at times…
[Corrected, thanks. For some strange reason I didn’t notice any dissonance in having two names for the same object during proofreading… -T]
21 November, 2012 at 3:20 am
Qiaochu Yuan
So it seems to me like a closed graph theorem for a category of sets and functions indicates that that category embeds as a natural subcategory of some category of sets and relations. For example, there is a category whose objects are groups and whose morphisms are relations between groups (that is, subgroups of their product) where composition is given by composition of relations. One might also call these categories of correspondences after the example of algebraic geometry.
21 November, 2012 at 8:07 am
Anonymous
Related to theorem 2: affine spaces/affine maps obey the same principle. [Added to the list, thanks -T.]
Categorically, a graph of a morphism f can be constructed by taking equalizer of two morphisms but I’m unsure if this could lead to a categorical characterization of closed graph theorem.
but I’m unsure if this could lead to a categorical characterization of closed graph theorem.
21 November, 2012 at 8:15 am
Anonymous
Typo: f: X\to Y, with graph \{(x,Tx)\}. One of f or T should be edited!
21 November, 2012 at 9:54 am
Terence Tao
One possible further addition to the list would be a closed graph theorem in the spirit of Theorem 6 for the category of finite etale covers of a fixed variety (without any need to assume normality or projectiveness, though I am not sure whether one can drop characteristic zero), basically because the degree argument used in the proof of Theorem 6 should also work in this category (though I am not 100% certain of this…). This should also be morally equivalent to the closed graph theorem for finite G-sets, where G is the etale fundamental group.
[ADDED LATER: it seems that in order for this to work, it is not enough for the graph of the putative morphism to be Zariski-closed; it must also be a finite etale cover of the base variety.]
21 November, 2012 at 2:49 pm
gowers
A very nice post. The closed graph theorem for Banach spaces is a good example of a theorem that is often lectured in a way I dislike: you’re told the statement and the proof and then expected to be able to apply it. As a result, I spent several years not really understanding it properly. It was OK if the question said “By using the closed graph theorem, prove that X,” but how was one to spot for oneself that the closed graph theorem might be useful? After seeing enough applications I eventually understood the answer (or more likely an answer). A function is continuous if
is continuous if  whenever
whenever 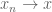 . But if the function
. But if the function  is a linear map between Banach spaces, then the closed graph theorem allows you to get away with establishing a weaker fact: it is enough to show that if
is a linear map between Banach spaces, then the closed graph theorem allows you to get away with establishing a weaker fact: it is enough to show that if 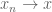 and
and 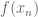 converges to something, then that something must be
converges to something, then that something must be 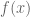 . In other words, we want to prove that
. In other words, we want to prove that  and can give ourselves a big leg up by assuming that
and can give ourselves a big leg up by assuming that 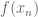 is a convergent sequence.
is a convergent sequence.
21 November, 2012 at 6:05 pm
Marcelo de Almeida
Reblogged this on Being simple.
22 November, 2012 at 7:27 pm
Marcelo de Almeida
A great post. Clarify in many ways the form of look the closed graph theorem by means of the essential structure
23 November, 2012 at 1:25 am
Milad
Reblogged this on Milad Ebrahimpour 's Blog.
29 November, 2012 at 12:36 pm
Closed Graph Theorem in Various Categories « Francis' Math Blog
[…] found this interesting blog post on Terence Tao’s blog about various analogs of the closed graph theorem […]
30 November, 2012 at 11:53 am
Lars Hormander « What’s new
[…] symplectic form on ; this is another instantiation of the closed graph theorem, as mentioned in this previous post. This graph is known as the canonical relation for the (putative) FIO that is associated to . To […]
27 April, 2013 at 9:26 pm
Notes on the classification of complex Lie algebras | What's new
[…] the graph is that of a Lie algebra isomorphism by the Lie algebra closed graph theorem (see this previous blog post). Since , we see that restricts to the graph of the identity on , and the claim […]
6 December, 2013 at 9:50 pm
Chien
Please help me find a discontinuous linear mapping T:X→Y such that T(X)=Y and X,Y are Banach but T is not open. Thanks you
17 October, 2014 at 11:54 pm
A closed graph theorem in dcpo’s | polmath
[…] Today I will add one closed graph type theorem to the list made by Terence Tao in his post Closed graph theorem in various categories. […]
8 June, 2019 at 10:47 pm
Matthias Hübner
A little typo after Theorem 6: should be “cuspidal”.
8 June, 2019 at 11:34 pm
Matthias Hübner
I appreciate John Gowers’ 1. comment: Theorem 5 (Closed graph theorem (point set topology)) is indeed valid more generally. Wikipedia https://en.wikipedia.org/wiki/Closed_graph_theorem has it that if X is a topological space and Y is a compact Hausdorff space, then the graph of f: X->Y is closed iff f is continuous.
But as John Gowers correctly points out, “continuous implies closed graph” holds if Y is Hausdorff, and for “closed graph implies continuous” compactness of Y is enough. For an indirect proof of the latter, assume f is not continuous at a certain x in X, so a net x_i in X converging to x “witnesses” the discontinuity – f(x_i) stays away from f(x). A subnet of f(x_i) converges to a y in Y (by compactness) different from f(x), so the graph of f is not closed at (x, f(x)).
20 October, 2019 at 1:05 pm
The topological closed graph theorem – johngowe.rs
[…] are a number of theorems in various settings that link continuity of a function (fcolon X to Y) to closedness of that […]