This is the seventh thread for the Polymath8b project to obtain new bounds for the quantity
either for small values of (in particular
) or asymptotically as
. The previous thread may be found here. The currently best known bounds on
can be found at the wiki page.
The current focus is on improving the upper bound on under the assumption of the generalised Elliott-Halberstam conjecture (GEH) from
to
. Very recently, we have been able to exploit GEH more fully, leading to a promising new expansion of the sieve support region. The problem now reduces to the following:
Problem 1 Does there exist a (not necessarily convex) polytope
with quantities
, and a non-trivial square-integrable function
supported on
such that
![{R + R \subset \{ (x,y,z) \in [0,4]^3: \min(x+y,y+z,z+x) \leq 2 \},}](https://s0.wp.com/latex.php?latex=%7BR+%2B+R+%5Csubset+%5C%7B+%28x%2Cy%2Cz%29+%5Cin+%5B0%2C4%5D%5E3%3A+%5Cmin%28x%2By%2Cy%2Bz%2Cz%2Bx%29+%5Cleq+2+%5C%7D%2C%7D&bg=ffffff&fg=000000&s=0&c=20201002)
when
;
when
;
when
;
and such that we have the inequality
An affirmative answer to this question will imply on GEH. We are “within two percent” of this claim; we cannot quite reach
yet, but have got as far as
. However, we have not yet fully optimised
in the above problem. In particular, the simplex
is now available, and should lead to some noticeable improvement in the numerology.
There is also a very slim chance that the twin prime conjecture is now provable on GEH. It would require an affirmative solution to the following problem:
Problem 2 Does there exist a (not necessarily convex) polytope
with quantities
, and a non-trivial square-integrable function
supported on
such that
![{R + R \subset \{ (x,y) \in [0,4]^2: \min(x,y) \leq 2 \}}](https://s0.wp.com/latex.php?latex=%7BR+%2B+R+%5Csubset+%5C%7B+%28x%2Cy%29+%5Cin+%5B0%2C4%5D%5E2%3A+%5Cmin%28x%2Cy%29+%5Cleq+2+%5C%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002)
when
;
when
;
and such that we have the inequality
We suspect that the answer to this question is negative, but have not formally ruled it out yet.
For the rest of this post, I will justify why positive answers to these sorts of variational problems are sufficient to get bounds on (or more generally
).
— 1. Crude sieve bounds —
Let the notation be as in the Polymath8a paper, thus we have an admissible tuple , a residue class
with
coprime to
for all
, and an asymptotic parameter
going off to infinity. It will be convenient to use the notation
We let be the interval
and for each fixed smooth compactly supported function , we let
denote the divisor sum
We wish to understand the correlation of various products of divisor sums on . For instance, in this previous blog post, the asymptotic
was established whenever one has the support condition
where is the outer edge of the support of
, and
We are now interested in understanding the asymptotics when (2) fails. We have a crude pointwise upper bound:
Lemma 3 Let
be a fixed smooth compactly supported function. Then for any natural number
,
for any fixed
. More generally, for any fixed number
of fixed smooth compactly supported functions, one has
Proof: We extend smoothly to all of
as a compactly supported function, and write the Fourier expansion
for some rapidly decreasing function . Then
Taking absolute values, we conclude that
Since , the first claim now follows from the rapid decrease of
. To prove the second claim, we use the first claim to bound the left-hand side of (3) by
Bounding
and
the claim follows after a change of variables.
Lemma 4 For each
, let
and
be fixed, and let
be fixed smooth compactly supported functions. Then
for any
and
, where
is the least prime factor of
.
The intuition here is that each of the is mostly bounded and mostly supported on the
for which
is almost prime (so in particular
is bounded), which has a density of about
in
.
Proof: From (3) (and bounding ), we can bound the left-hand side of (4) by
Let be a small fixed number (
will do). For each
, we let
be the prime factors of
in increasing order (counting multiplicity), and let
be the largest product of consecutive primes factors that is bounded by
. In particular, we see that
and hence
which in particular implies that . This implies that
Now observe that , where
is
-rough (i.e. no prime factors less than
). In particular, it is
-rough. Thus we can bound the left-hand side of (4) by
By using a standard upper bound sieve (and taking small enough), the quantity
may be bounded by
Since , we can thus bound the left-hand side of (4) by
We can bound this by
(strictly speaking one has some additional contribution coming from repeated primes , but these can be eliminated in a number of ways, e.g. by restricting initially to square-free
). By Mertens’ theorem we have
\endand then by summing the series in , we can bound the left-hand side of (4) by
which for large enough is
as required. This proves (4).
The proof of (5) is similar, except that (assuming small, as we may)
is forced to be at least
, and
is at most
. From this we may effectively extract an additional factor of
(times a loss of
due to having to reduce
to
), which gives rise to the additional gain of
.
— 2. The generalised Elliott-Halberstam conjecture —
We begin by stating the conjecture more formally, using (a slightly weaker form of) the version from this paper of Bombieri, Friedlander, and Iwaniec. We use the notation from the Polymath8a paper.
Conjecture 5 (GEH) Let
for some fixed
, be such that
, and let
be coefficient sequences at scale
. Then
for any fixed
.
We use GEH to refer to the assertion that holds for all
. As shown by Motohashi, a modification of the proof of the Bombieri-Vinogradov theorem shows that
is true for
. (It is possible that some modification of the arguments of Zhang give some weak version of GEH for some
slightly above
, but we will not focus on that topic here.)
For our purposes, we will need to apply GEH to functions supported on products of primes for a fixed
(generalising the von Mangoldt function, which is the focus of the Elliott-Halberstam conjecture EH). More precisely, we have
Proposition 6 Assume
holds. Let
and
be fixed, let
, and let
be a fixed smooth function. Let
be the function defined by setting
whenever
is the product of
distinct primes
with
for some fixed
, and
otherwise. Then
for any fixed
.
Remark: it may be possible to get some version of this proposition just from EH using Bombieri’s asymptotic sieve.
Proof: (Sketch) This is a standard partitioning argument (not sure where it appears first, though). We choose a fixed that is sufficiently large depending on
. We can decompose the primes from
to
into
intervals
. This splits
into
pieces, depending on which intervals the
lie in. The contribution when two primes lie in the same interval, or when the products of the specified intervals touches the boundary of
, can be shown to be negligible by crude divisor function estimates if
is large enough (a similar argument appears in the Polymath8a paper), basically because there are only
such terms, and each one contributes
to the total. For the remaining pieces, one can approximate
by a constant, up to errors which can also be shown to be negligible by crude estimates for
large enough (each term contributes
), and then
can be modeled by a convolution of
coefficient sequences at various scales between
and
, at which point one can use GEH to conclude.
Corollary 7 Assume
holds for some
. Let
and
be fixed, let
be fixed and smooth, and let
be as in the previous proposition. Let
be a divisor sum of the form
where
are coefficients supported on the range
. Then
for any fixed
.
Similarly for permutations of the
.
Proof: (Sketch) We can rearrange as
Using the previous proposition, and the Chinese remainder theorem, we may approximate by
plus negligible errors (here we need the crude bounds on and some standard bounds on the divisor function), thus
A similar argument gives
and the claim follows by combining the two assertions.
Next, from Mertens’ theorem one easily verifies that
where is the expected density of primes in
, and the measure on
is the one induced from Lebesgue measure on the first
coordinates
. (One could improve the
term to
here by using the prime number theorem, but it isn’t necessary for our analysis.)
Applying (1), we thus have
Corollary 8 Assume
holds for some
. Let
and
be fixed, let
be fixed and smooth, and let
be as in the previous proposition. For
, let
be smooth compactly supported functions with
. Then
where
and
for
.
— 3. Some integration identities —
Lemma 9 Let
be a smooth function. Then
where
.
Proof: Making the change of variables , the integral
can be written as
which by symmetry is equal to
which after expanding out the square and using symmetry is equal to
and the claim follows from the fundamental theorem of calculus.
Iterating this lemma times, we conclude that
for any , where the first integral is integrated using
. In particular, discarding the final term (which is non-negative) and then letting
, we obtain the inequality
In fact we have equality:
Proposition 10 Let
be smooth. Then
In particular, by depolarisation we have
for smooth
.
Proof: Let be a small quantity, and write
From Lemma 9 we have
where
From another application of Lemma 9 we have
where
Iterating this, we see that
for any , where
If , then
vanishes, thus
where
and . By Fubini’s theorem, we have
Discarding the constraints and using
and
, we conclude that
Summing over using (6), we see that
since by the smoothness of
, we conclude that
and thus by (9)
Direct computation also shows that , hence
and thus
But by the monotone convergence theorem, as ,
converges to
Thus we can complement (6) with the matching upper bound, giving the claim.
We can rewrite the above identity using the following cute identity (which presumably has a name?)
Lemma 11 For any positive reals
with
, one has
where
ranges over the permutations of
.
Thus for instance
and so forth.
Proof: We induct on . The case
is trivial. If
and the claim has already been proven for
, then from induction hypothesis one has
for each . Summing over
, we obtain the claim.
Proposition 12 Let
be smooth. Then
Proof: Average (7) over permutations of the and use Lemma 11.
This gives us a variant of
Corollary 13 Assume
holds for some
. For
, let
be smooth compactly supported functions with
. Then
where
for
.
Proof: Let . By (5), we have
so by paying a cost of , we may restrict to
which are
-rough, and are thus of the form
for some
and
. For
(restricting to squarefree integers
to avoid technicalities), we have
and similarly for . Using this and Corollary 13, we may write the left-hand side of (10) as
Sending and using dominated convergence and Proposition 11, we obtain the claim.
Taking linear combinations, we conclude the usual “denominator” asymptotic
with
whenever is supported on a polytope
(not necessarily convex) with
and is a finite linear combination of tensor products of smooth compactly supported functions. We use this as a replacement for the denominator estimate in this previous blog post, we obtain the criteria described above.

117 comments
Comments feed for this article
29 January, 2014 at 12:20 am
Eytan Paldi
In the second product above lemma 4, the upper index should be . [Corrected, thanks – T.]
. [Corrected, thanks – T.]
29 January, 2014 at 4:50 am
Aubrey de Grey
I think in both Problem 1 and Problem 2, the range integrated over that refers to epsilon2 should be “<=", not "<". At least, that's what it was in Problem 1 in the previous post.
[The two are equivalent, since the difference has measure zero – T.]
29 January, 2014 at 4:58 am
Jonas KAHN
Probably not useful since it cannot be pushed further, but it’s obvious we may find F as close to 2 as we may want in Problem 1 (in Problem 2 as well for that matter): . Define
. Define  on the three “rods”
on the three “rods” ![[0, \epsilon]^{2} \times [0, 2 - 2\epsilon]](https://s0.wp.com/latex.php?latex=%5B0%2C+%5Cepsilon%5D%5E%7B2%7D+%5Ctimes+%5B0%2C+2+-+2%5Cepsilon%5D&bg=ffffff&fg=545454&s=0&c=20201002) and its symmetries as:
and its symmetries as: :
: 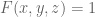 if
if ![(x,y) \in [0,\epsilon/2]^2 \cup [\epsilon/2, \epsilon]^2](https://s0.wp.com/latex.php?latex=%28x%2Cy%29+%5Cin+%5B0%2C%5Cepsilon%2F2%5D%5E2+%5Ccup+++%5B%5Cepsilon%2F2%2C+%5Cepsilon%5D%5E2&bg=ffffff&fg=545454&s=0&c=20201002) , and
, and 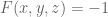 if
if ![(x,y) \in [0,\epsilon/2]\times [\epsilon/2, \epsilon] \cup [\epsilon/2, \epsilon] \times [0,\epsilon/2]](https://s0.wp.com/latex.php?latex=%28x%2Cy%29+%5Cin+%5B0%2C%5Cepsilon%2F2%5D%5Ctimes+%5B%5Cepsilon%2F2%2C+%5Cepsilon%5D+%5Ccup++%5B%5Cepsilon%2F2%2C+%5Cepsilon%5D+%5Ctimes+%5B0%2C%5Cepsilon%2F2%5D++&bg=ffffff&fg=545454&s=0&c=20201002) .
. on the small cube
on the small cube ![[0, \epsilon]^3](https://s0.wp.com/latex.php?latex=%5B0%2C+%5Cepsilon%5D%5E3&bg=ffffff&fg=545454&s=0&c=20201002) .
. .
.
Take
* if
* symmetric definition on the other rods.
*
We get factor
(We could also use the sum of the functions on the small cube, with no big difference, and it could be seen as a sum of three iid variables on this cube.)
29 January, 2014 at 8:49 am
polikimre
My background is numerical optimization and not number theory, but I was wondering if Problems 1 and 2 could be discretized and solved numerically. Define a fine grid on the cube, define F on the grid points and interpolate either piecewise or with any other method. R is defined implcitly as the support of F. Then convert all constraints into constraints on the pointwise values. It wouldn’t be a small problem, but things are mostly quadratic or cubic so it might be tractable.
29 January, 2014 at 11:32 am
arch1
It seems to me (naively, as there’s a lot of this I’m not understanding) that some global optimization heuristic such as Simulated Annealing might be applicable to the formulation you describe (I’m guessing that in addition to the scads of pointwise F values, the 3 epsilons would need to be explicit optimization parameters). It would be interesting to hear someone with the big picture weigh in.
29 January, 2014 at 9:51 am
Jonas KAHN
By the way, a strictly bigger than the simplex is available, too:
strictly bigger than the simplex is available, too:
 .
.
29 January, 2014 at 1:51 pm
Terence Tao
This is indeed an interesting new region to use, although it doesn’t quite strictly contain the simplex: , for instance, is in the simplex but not in this region. With recent developments it may no longer be necessary to test out this polytope, but we can certainly keep it in reserve in case a problem develops with the simplex.
, for instance, is in the simplex but not in this region. With recent developments it may no longer be necessary to test out this polytope, but we can certainly keep it in reserve in case a problem develops with the simplex.
29 January, 2014 at 2:00 pm
Jonas KAHN
Right, even if the counter-example should be .
.
29 January, 2014 at 10:50 am
Eytan Paldi
Is it possible to relax the polytope condition on to a (finite) union of disjoint polytopes ?
to a (finite) union of disjoint polytopes ?
29 January, 2014 at 11:57 am
arch1
If not, couldn’t you just replace any solution based on a disjoint-polytope R, with an essentially equivalent one based on a single-polytope R by adding arbitrarily skinny umbilical cords?
29 January, 2014 at 12:27 pm
Eytan Paldi
It seems that (instead of the polytope property) only measurability is really needed (the finite union of polytopes was stated only to simplify the optimization).
measurability is really needed (the finite union of polytopes was stated only to simplify the optimization).
29 January, 2014 at 1:38 pm
Terence Tao
This should be OK (and probably one can allow R to be any compact set, though there may be some technical issues regarding approximating F by smooth functions while staying supported in the interior of R and respecting all the marginal conditions).
29 January, 2014 at 11:36 am
Gil Kalai
Does problem 2 indicates a method/idea to overcome the “parity problem” (under GEH)?
29 January, 2014 at 1:08 pm
Pace Nielsen
On the previous thread, James said “I’d be skeptical the parity barrier isn’t hiding somewhere.” I agree. I did a quick computation, using on the region
on the region  and (if I didn’t make a mistake) the optimal value that pops out is exactly 2, for any epsilon.
and (if I didn’t make a mistake) the optimal value that pops out is exactly 2, for any epsilon.
29 January, 2014 at 2:40 pm
Terence Tao
That’s reassuring; if our calculations indicated we had somehow stumbled accidentally into a way to somehow sneak past the parity barrier, I would think it much more likely that there was an error in the calculation than that we had unwittingly defeated one of the most notorious barriers in analytic number theory. I agree with James that the barrier is still present, it’s just that we can’t quite see it right now; instead of having a solid iron door between us and the twin prime conjecture, we’ve now moved into a position where there is a dark corridor between us and the conjecture, but presumably the parity barrier is still lurking behind the darkness.
A bit more formally, we used to play exclusively with sieves which were anticorrelated with both the Mobius function
which were anticorrelated with both the Mobius function 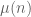 and its shift
and its shift  , which meant that weighted to
, which meant that weighted to  , the probability of n being prime is at most 1/2, and the probability that n+2 is at most 1/2, so one cannot force n and n+2 to both be prime just from “one-point correlations” on how likely n and n+2 are separately to be prime.
, the probability of n being prime is at most 1/2, and the probability that n+2 is at most 1/2, so one cannot force n and n+2 to both be prime just from “one-point correlations” on how likely n and n+2 are separately to be prime.
Now that we are moving beyond the unit cube, we are permitted to use sieves that correlate with
that correlate with 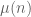 and/or
and/or  . For instance, one extreme is to take
. For instance, one extreme is to take  , in which case we have a 100% correlation with
, in which case we have a 100% correlation with 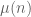 (and a 100% chance asymptotically for n to be prime), but no non-trivial control on the probability that n+2 is prime. Or one could take
(and a 100% chance asymptotically for n to be prime), but no non-trivial control on the probability that n+2 is prime. Or one could take  , or some convex combination of
, or some convex combination of  and
and 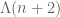 . In none of these situations can we get “probability that n is prime” + “probability that n+2 is prime” to exceed 1, but it’s not clear whether there is a systematic obstruction that guarantees that this is impossible. As James points out, all the new sieves
. In none of these situations can we get “probability that n is prime” + “probability that n+2 is prime” to exceed 1, but it’s not clear whether there is a systematic obstruction that guarantees that this is impossible. As James points out, all the new sieves  we play with should (conjecturally at least) still be anticorrelated with
we play with should (conjecturally at least) still be anticorrelated with  , but this by itself does not seem to block the possibility of a sieve
, but this by itself does not seem to block the possibility of a sieve  for which n and n+2 both have (say) a 2/3 chance of being prime. (Consider for instance a scenario in which n and n+2 are both prime with probability 5/12, that n is prime and n+2 has an even number of prime factors with probability 1/4 and vice versa for n+2 and n, and finally n and n+2 both have an even number of prime factors with probability 1/12.)
for which n and n+2 both have (say) a 2/3 chance of being prime. (Consider for instance a scenario in which n and n+2 are both prime with probability 5/12, that n is prime and n+2 has an even number of prime factors with probability 1/4 and vice versa for n+2 and n, and finally n and n+2 both have an even number of prime factors with probability 1/12.)
29 January, 2014 at 4:27 pm
Axel Obermeier
I think that there might be a mistake hiding in the derivation of Problem 2 (or in my calculations below) – otherwise I might have found an F/R-combination which satisfies Problem 2.
I should add that I am far out of my league as far as polymath8a/b is concerned, but I have been following it with interest and was intrigued by the apparent simplicity of Problem 2 (at least in terms of mathematical concepts involved). In a procrastination-induced rush of hubris, I tried to find an F/R combination, and it is with tremendous hesitation that I post this here – most probably I overlooked a condition or a factor somewhere, which collapses my very simplistic argument.
I have correspondingly double- and triple-checked my calculations, and still can’t believe my own lying eyes and calculations. Please excuse me wasting your time if a mistake is readily apparent nevertheless.
While I have seen how polymath8a in particular exploited the splitting of parameters into separate parts, the inherent symmetry of Problem 2 led me to start with and
and  and with the biggest possible
and with the biggest possible  , namely $R=[0,1]\times[0,2] \cup [0,2]\times[0,1]$.
, namely $R=[0,1]\times[0,2] \cup [0,2]\times[0,1]$.
Problem 2 is then equivalent to finding such that:
such that:

 of the L-shaped
of the L-shaped  .
.
which is just the restriction of the problem to the lower part
Defining on
on  as
as 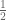 when
when  (second inequality is strict) and as
(second inequality is strict) and as  when
when  , we see that the marginal conditions are satisfied, and integrating is easy:
, we see that the marginal conditions are satisfied, and integrating is easy:
The result of the left-hand side is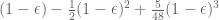 , whereas the right-hand side is
, whereas the right-hand side is 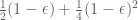 . Substracting the right from the left, we can see (by plotting or by an actual discussion of the curve) that the inequality holds for
. Substracting the right from the left, we can see (by plotting or by an actual discussion of the curve) that the inequality holds for  (of course, the root, as well as the maximum could easily be determined).
(of course, the root, as well as the maximum could easily be determined).
Fearing a mistake, I went back again to the original formulation and tried for my F/R-combination, The first term on the left-hand side is then
for my F/R-combination, The first term on the left-hand side is then  .
.
For symmetry reasons, the second term is exactly the same. The right-hand side equals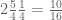 , and thus we have
, and thus we have 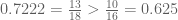 .
.
29 January, 2014 at 4:50 pm
Axel Obermeier
Oh how I wish I could eat my words, obviously is not satisfied. Prof. Tao, you’re welcome to delete my comments (in fact I’d be very thankful).
is not satisfied. Prof. Tao, you’re welcome to delete my comments (in fact I’d be very thankful).
29 January, 2014 at 5:10 pm
Pace Nielsen
Axel, we’ve all made similar mistakes while working on this problem. (One of my early mistakes was forgetting the cross terms after squaring!) I’m just glad to see others join the “fray”. Keep it up!
30 January, 2014 at 5:28 am
Axel Obermeier
@Pace Nielson, thank you for the encouragement – I shouldn’t have tried to do this in the middle of the night (MEST here).
Similarly, I should probably stop digging myself into a deeper hole, but I couldn’t keep myself from tinkering a bit more (in the process finding another error that I’d made before – the equivalence above is wrong).
So, if I may be allowed another try:![R:=\left([0,\frac{2}{3}]\times[0,\frac{4}{3}]\cup[0,\frac{4}{3}]\times[0,\frac{2}{3}]\right)\setminus[0,\frac{1}{3}]^2](https://s0.wp.com/latex.php?latex=R%3A%3D%5Cleft%28%5B0%2C%5Cfrac%7B2%7D%7B3%7D%5D%5Ctimes%5B0%2C%5Cfrac%7B4%7D%7B3%7D%5D%5Ccup%5B0%2C%5Cfrac%7B4%7D%7B3%7D%5D%5Ctimes%5B0%2C%5Cfrac%7B2%7D%7B3%7D%5D%5Cright%29%5Csetminus%5B0%2C%5Cfrac%7B1%7D%7B3%7D%5D%5E2&bg=ffffff&fg=545454&s=0&c=20201002) , which, as a subset of
, which, as a subset of 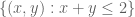 satisfies the Minkowski-sum condition
satisfies the Minkowski-sum condition  .
.
Define
Again, set and define
and define  on
on  as
as  for
for  (second ineq. strict) and as
(second ineq. strict) and as  for
for  . Extend to
. Extend to  with
with  .
.
The marginal conditions are satisfied and we see that Problem 2 is equivalent to – due to symmetry the second term on the left-hand side is the same and we just divided by two.
– due to symmetry the second term on the left-hand side is the same and we just divided by two.
The first integral actually only goes to because the rest cancels in the same way as the marginal condition.
because the rest cancels in the same way as the marginal condition.
Putting this into Maple – I wanted to avoid making mistakes in the integration – the inequality seems to hold for (the actual discussion of the curve would be tedious).
(the actual discussion of the curve would be tedious).
The code (using z for ):
):
n:=1/2
plot(int((int(x^n, x = (1-z)*(1/3) .. 4/3))^2, y = 0 .. (1-z)*(1/3))+int((int(y^n, x = 0 .. (1-z)*(1/3))-(int(y^n, x = (1-z)*(1/3) .. y))-(int(x^n, x = y .. 4/3)))^2, y = (1-z)*(1/3) .. 2/3*(1-z))-2*(int(int(x^(2*n), x = (1-z)*(1/3) .. 4/3), y = 0 .. (1-z)*(1/3))+int(int(x^(2*n), x = y .. 2/3*(1-z)), y = (1-z)*(1/3) .. 2/3*(1-z))), z = 0 .. 1)
30 January, 2014 at 7:22 am
Axel Obermeier
Too excited again… Made a mistake in the integral limits which kills the inequality (second-to-last integral should go from x=y..4/3). Serves me right for trying to break the parity problem with stone-age methods…
30 January, 2014 at 7:23 am
Bogdan
The inequality does not hold, should be a mistake in your Maple code. In general, if the marginal conditions are satisfied with ,
, 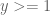 (as it is in your example), then I could take
(as it is in your example), then I could take  and avoid
and avoid  trick, but in this case (as far as I remember) there was a strict proof that such function cannot exist.
trick, but in this case (as far as I remember) there was a strict proof that such function cannot exist.
29 January, 2014 at 1:01 pm
Pace Nielsen
It appears that Zeno’s paradox has fallen prey to James’ newest idea! If I haven’t made any mistakes, I get . I’ve now double checked all of the integrals (and in the process actually found an error from my previous computation, which was *lowering* the needed value). Those who want to check the details can look at the three documents:
. I’ve now double checked all of the integrals (and in the process actually found an error from my previous computation, which was *lowering* the needed value). Those who want to check the details can look at the three documents:
1. A pdf listing all integrals involves, choices of epsilon, etc…: http://www.math.byu.edu/~pace/BddGapsSize6.pdf
2. The Mathematica notebook doing the computation: http://www.math.byu.edu/~pace/Computation-BddGapsSize6.nb
3. Another Mathematica notebook, with nice pictures of the regions involved: http://www.math.byu.edu/~pace/RegionPlots-BddGapsSize6.nb
If anyone finds an error, just let me know.
29 January, 2014 at 1:48 pm
Terence Tao
This sounds like excellent news! I’ll try to confirm the polynomial decomposition at least. It looks like James has some independent code for this sort of thing, so hopefully we’ll get confirmation soon. The numbers seem to be reasonable though, and it sounds like you have a little bit of room in optimising the epsilons and degrees to make the value a little bigger, so we have a bit of cushion for numerical error etc. (Now that epsilon is the nice round value of 1/4, presumably we can find an F which is piecewise polynomial with rational coefficients and still gets above 2, so that we can work with exact arithmetic and not have to worry about roundoff error, at least.)
It’s interesting that epsilon has been slowly growing larger as we keep unlocking more regions of space to optimise over, but I guess this makes sense: the more room there is beyond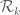 , the more profit one can make off of a large value of epsilon, thus offsetting the cost of shrinking the J integrals (which, intuitively, is a cost which is more or less insensitive to how much more room one has).
, the more profit one can make off of a large value of epsilon, thus offsetting the cost of shrinking the J integrals (which, intuitively, is a cost which is more or less insensitive to how much more room one has).
29 January, 2014 at 2:04 pm
Pace Nielsen
I followed James’s lead from his code attached to his preprint. Just as he does, at the very end of my code all polynomial approximations are made to have rational coefficients. So the exact arithmetic part is being done.
On the increasing epsilon, I wonder if Eytan could do an analysis similar to the one he did before (for![\varepsilon\in (1/2,1]](https://s0.wp.com/latex.php?latex=%5Cvarepsilon%5Cin+%281%2F2%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) ) but for this larger simplex.
) but for this larger simplex.
By the way, regarding unlocking space– that is what motivated me to break up (what I call in my notes) the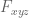 region into the three pieces. After the split, the biggest piece (
region into the three pieces. After the split, the biggest piece ( ) appears in only one marginal condition.
) appears in only one marginal condition.
29 January, 2014 at 3:03 pm
Eytan Paldi
In the wiki page on the variational problem, Pace’s newest lower bound record (2.0009) for should be for
should be for 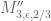 (i.e. for
(i.e. for 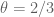 instead of
instead of 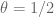 ).
).
29 January, 2014 at 3:30 pm
Aubrey de Grey
Um – should it? Surely that subscript refers to the reciprocal of the edge-length of the cube that MUST bound the supported region, rather than the reciprocal of the edge-length of the smallest cube that actually bounds the region on which the calculation was done?
29 January, 2014 at 4:10 pm
Eytan Paldi
Note that is at least
is at least  (which for
(which for
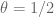 is
is  – which is larger than our
– which is larger than our 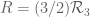 – which is the
– which is the  for
for 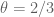 .
.
29 January, 2014 at 4:17 pm
Terence Tao
Hmm, fair point. Maybe I’ll call it (as I don’t want to artificially set
(as I don’t want to artificially set  to 2/3, since that’s not the value of
to 2/3, since that’s not the value of  for which GEH holds), with the hat meant to indicate that we get to add the corners of the simplex as opposed to having to truncate it.
for which GEH holds), with the hat meant to indicate that we get to add the corners of the simplex as opposed to having to truncate it.
EDIT: have now added a table to the Selberg sieve wiki page, http://michaelnielsen.org/polymath1/index.php?title=Selberg_sieve_variational_problem , to summarise all the notation.
29 January, 2014 at 4:23 pm
Eytan Paldi
Anyway, the appropriate for this new M-value should be defined.
for this new M-value should be defined.
29 January, 2014 at 5:11 pm
Pace Nielsen
Nice tables! Thank you for doing all of that.
29 January, 2014 at 5:55 pm
Aubrey de Grey
This new table is most helpful – thank you Terry!
Doesn’t there need to be some dependence on epsilon in the polytope constraints of the M”_k,epsilon rows?
Also: maybe the “non-convex” polytope can be described in a k-independent form, which I think is that more than half of the t_i must be at least the sum of all t_i minus 1. (I hope that an intelligible notation for this constraint can be devised!) This may perhaps be useful in the soon-to-be-refocused-upon unconditional setting, especially bearing in mind that James’s new trick somewhat diminishes (I think) the dominance of the 2/theta-sized simplex’s contribution to R+R for larger k.
29 January, 2014 at 8:56 pm
Terence Tao
The table only lists the constraints for the overall polytope R. The epsilon parameter affects how one partitions the polytope, the marginal conditions imposed on the function on the polytope, and the domain of integration of the J integrals.
I think that once the k=3 breakthrough is confirmed, we might experiment with a number of the different polytope options for other small values of k, with an eye to extrapolating out to the 50s where the Bombieri-Vinogradov results are currently living. My feeling is that all of these expansions only improve M by a factor of O(1/k) or so, corresponding to an improvement in k by O(1) – but when k is already around 50, this is not so bad of a gain…
29 January, 2014 at 10:10 pm
Terence Tao
I did a number of spot checks on Pace’s polytope decomposition and it looks good, but it got fairly tedious, and I thought that perhaps it would be better to spend time to find a different way to compute the same quantity, as this might give a more convincing confirmation of the number.
I realised that there is an adjoint problem to the problem, in terms of a two-dimensional function G. Recall that M is the best constant in the inequality
problem, in terms of a two-dimensional function G. Recall that M is the best constant in the inequality
where F is symmetric, supported on , and has the vanishing marginal condition
, and has the vanishing marginal condition 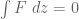 when
when  .
.
I claim that M is also the best constant in the adjoint inequality
whenever G is symmetric and supported on the disconnected region , and the function
, and the function 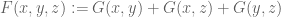 obeys the vanishing marginal condition. Let’s just show that (**) holds for the M appearing in (*); the converse implication is also true, but the forward implication is the relevant one for the purposes of lower bounding M. We can write the left-hand side of (**) using symmetry, the vanishing marginal condition, and Cauchy-Schwarz as
obeys the vanishing marginal condition. Let’s just show that (**) holds for the M appearing in (*); the converse implication is also true, but the forward implication is the relevant one for the purposes of lower bounding M. We can write the left-hand side of (**) using symmetry, the vanishing marginal condition, and Cauchy-Schwarz as
Applying (*) and rearranging, we obtain (**).
The left-hand side of (**) can also be simplified a bit using symmetry as
The vanishing marginal condition takes the form
for .
.
We are now in a variational problem similar to the original one (*), except that all the domains of integration are basically two dimensional. In particular, when , it looks like one should decompose the support of G into seven regions (plus the reflections of five of these, so 12 regions in all):
, it looks like one should decompose the support of G into seven regions (plus the reflections of five of these, so 12 regions in all):
One can set G to be a polynomial on each of these domains (with symmetry enforced on E and F), with the vanishing marginal condition (***) being a set of linear constraints (there is one set involving A,C,D, there is another involving B,G, and a third set involving B,F). Both sides of (**) are then quadratic functions of the coefficients. This looks like a problem of slightly lower complexity than the one Pace was using, and hopefully a modification of Pace’s code will then give a separate confirmation of the 2.0009 result (and maybe it could even improve it a little, due to the more efficient representation of the function). I might try tinkering with this myself, although I’ve not used Mathematica before, so I don’t know how successful I’ll be.
30 January, 2014 at 7:52 am
Pace Nielsen
Terry, I hope you enjoy playing around with Mathematica. It can be a lot of fun.
There does seem to be one problem with your decomposition; I believe you want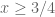 in
in 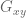 (so that it doesn’t overlap with
(so that it doesn’t overlap with  ). [Corrected, thanks – T.]
). [Corrected, thanks – T.]
For these two-dimensional regions, the function “RegionPlot” can be quite useful to double-check overlapping. For instance, to graph just type: The thing you should type is: RegionPlot[0 <= y <= 1/4 && 5/4-y <= x <= 5/4].
just type: The thing you should type is: RegionPlot[0 <= y <= 1/4 && 5/4-y <= x <= 5/4].
If the lines are not straight, increase the number of points by using the PlotPoints modifier.
30 January, 2014 at 10:23 am
Pace Nielsen
In the offset equation following “The left-hand side of (**) can also be simplified a bit using symmetry as…” I believe that in the first integrand the function should be squared.
should be squared.
This equation can be simplified further, using the vanishing marginals.
30 January, 2014 at 10:51 am
Terence Tao
Thanks for the correction! I was in fact in the process of simplifying the problem further, and have gotten to a point where one only needs to work with polynomials on three triangles ( ,
, 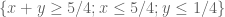 and
and  with a quite clean formula for the numerator and denominator. Details to follow soon…)
with a quite clean formula for the numerator and denominator. Details to follow soon…)
30 January, 2014 at 11:57 am
Terence Tao
I wrote up the formulation involving polynomials on these three triangles at
Click to access variational.pdf
The numerator is mildly messy, as are the linear constraints, but it still looks like a slightly simpler problem than the three-dimensional one. Unfortunately I don’t think I will be able to modify Pace’s Mathematica code (or more importantly, to debug the resulting modification) to implement this, but this should be doable by someone with better Mathematica skills than I.
30 January, 2014 at 12:50 pm
Eytan Paldi
In the proof of proposition 0.1, it seems that the marginal condition (0.2) should imply that the integration is over (instead of
(instead of  ).
).
30 January, 2014 at 12:55 pm
Terence Tao
Well, the two integrals are the same because G vanishes when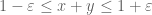 . I’ve made a few minor other corrections to the file, new version is at https://terrytao.files.wordpress.com/2014/01/variational1.pdf
. I’ve made a few minor other corrections to the file, new version is at https://terrytao.files.wordpress.com/2014/01/variational1.pdf
30 January, 2014 at 2:54 pm
Pace Nielsen
Terry, thank you for this nice file!
Just a small comment. In your decomposition, since you have broken symmetry (at least with the parts) one should not assume that the restriction of the function
parts) one should not assume that the restriction of the function  to these regions is symmetric. Because of this, I recommend replacing quantities like
to these regions is symmetric. Because of this, I recommend replacing quantities like  with
with 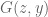 , because then it is much easier to keep track of which “copy” of
, because then it is much easier to keep track of which “copy” of  one is working on when we start decomposing the region further.
one is working on when we start decomposing the region further.
An example where this can be an issue arises in (0.6). I believe should rather be
should rather be 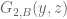 [the restriction of
[the restriction of  to the “other” copy of
to the “other” copy of  . Or, more easily,
. Or, more easily,  .
.
30 January, 2014 at 4:51 pm
Terence Tao
Good point; I’ve made the appropriate changes at the latest version: https://terrytao.files.wordpress.com/2014/01/variational2.pdf
30 January, 2014 at 8:19 pm
Pace Nielsen
I did the computation with the given integrals and am only getting or so, even for degrees up to 13. I’ve triple checked it now. But I’ve been awake too long to give it more thought tonight, so I’ll give it a good look in the morning!
or so, even for degrees up to 13. I’ve triple checked it now. But I’ve been awake too long to give it more thought tonight, so I’ll give it a good look in the morning!
By the way, in the last formula given for have you taken into account that we need to double the contributions of the parts from B,C,D, but not from E? (It just strikes me as strange that the coefficient for the E part is the same as for the others. Maybe this will make sense in the morning.)
have you taken into account that we need to double the contributions of the parts from B,C,D, but not from E? (It just strikes me as strange that the coefficient for the E part is the same as for the others. Maybe this will make sense in the morning.)
30 January, 2014 at 10:37 pm
Terence Tao
Hmm, that is odd; the first term in J alone should already give 1.5; admittedly, some of the later terms can be negative, but still the 1.55 value is surprising. Could you post the code?
One possibility is that one needs to partition A more. I guess this would be reflected in a slow convergence rate with respect to the degree. (Still, the fact that you can get up to degree 13 now is encouraging, hopefully once all the bugs are sorted out, we can get quite precise numerics now.)
As for the E vs. B,C,D issue, it comes from having broken the symmetry at an earlier stage of the argument. J is basically the inner product , that is to say
The fragment
of this is what is giving the B,C,D,E contributions. There is a reflected fragment
which would have contributions from reflections of B,C,D and a (reflected) contribution to E. Note that for (x,z) in E, both G_0(y,z) and G_0(x,y) can be nonzero, but for other regions, only one of the two is nonzero. This doubling up of the E contribution sort of cancels out the fact that E is its own reflection
31 January, 2014 at 5:42 am
Pace Nielsen
On page 4, is the last equality of the first offset equation correct? When I plot the region given by I do not get the same region as given by
I do not get the same region as given by 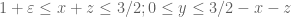 . For instance, if
. For instance, if 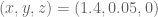 then this seems to live in the second region, but not the first.
then this seems to live in the second region, but not the first.
31 January, 2014 at 5:53 am
Pace Nielsen
Nevermind, I see now you are implicitly using the support of here to cover this.
here to cover this.
31 January, 2014 at 6:38 am
Pace Nielsen
You can find my code here: http://www.math.byu.edu/~pace/Computation-BddGaps6-2D.nb
31 January, 2014 at 9:29 am
Terence Tao
Thanks for this! It looks like the convergence is pretty slow, if degree 10 gives 1.51 and degree 13 gives 1.55. So probably there is a need to partition the big triangle further here (although this removes a lot of the supposed advantage of this framework.
I should be able to do this from the code you gave me, but it turns out that my Mathematica skills are so primitive I can barely run the notebook and tweak the parameters: could you give an explicit example of a low-degree choice for the polynomials Gmain, GA-GE, H1, H2 together with the values you computed for I, J? I can try to confirm these values with Maple (and also to convert things back into the original F-formulation using F(x,y,z)=G(x,y)+G(y,z)+G(z,x), to confirm that there wasn’t something going wrong with the calculations in my notes; also I want to see how accurate the eigenfunction equation is). If they check out then likely the problem is with the partitioning.
31 January, 2014 at 11:07 am
Pace Nielsen
I’ve replaced the Mathematica notebook with a new one which contains the explicit polynomials one gets from taking d=3, and it also gives the integral outputs. Use the same link above to get to it. You should be able to just copy and paste the information into Maple. (I turned the complicated fractions into floating point. To get the polynomials with the exact fractions, instead of evaluating “N[GMain]” just evaluate “Expand[GMain]” (after running all the other lines).
30 January, 2014 at 4:35 am
Eytan Paldi
Is it possible to relax the conditions on by enlarging it to
by enlarging it to ![[0, 2]^3](https://s0.wp.com/latex.php?latex=%5B0%2C+2%5D%5E3&bg=ffffff&fg=545454&s=0&c=20201002) and replacing the condition on
and replacing the condition on  by the (more flexible) condition on
by the (more flexible) condition on  as follows:
as follows:
(i) and
and
(ii) is outside the region containing
is outside the region containing  (as defined in problem 1.)
(as defined in problem 1.)
In addition, perhaps condition (ii) may be relaxed from a pointwise vanishing condition to a vanishing condition in some weaker sense (e.g. a certain type of vanishing marginals condition)?
30 January, 2014 at 9:13 am
Terence Tao
Yes, this should work. This would fit well with a grid-type scheme as suggested by polikimre above, although the constraint is nonlinear and may not be so easy to solve numerically (plus, I don’t have a good sense of how many grid points one would need to get a good approximation).
30 January, 2014 at 12:02 pm
Eytan Paldi
The idea is to avoid the many possible candidates for by converting the somewhat “too restrictive” constraint on
by converting the somewhat “too restrictive” constraint on 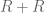 into a more efficient constraint (which is “really needed”) on
into a more efficient constraint (which is “really needed”) on  without the need to use fixed
without the need to use fixed  with the above property during
with the above property during  optimization.
optimization. representation (with appropriate partition) for which
representation (with appropriate partition) for which  is supported on the intersection of
is supported on the intersection of ![[0, 2]^3](https://s0.wp.com/latex.php?latex=%5B0%2C+2%5D%5E3&bg=ffffff&fg=545454&s=0&c=20201002) with the region containing
with the region containing 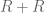 (as described in problem 1) – which should be very simple (in terms of the piecewise polynomial representation.)
(as described in problem 1) – which should be very simple (in terms of the piecewise polynomial representation.)
Instead of using (approximate) grid points, I suggest to use piecewise
30 January, 2014 at 5:11 pm
Eytan Paldi
Consequently, it seems that problem 1 can be modified for the (largest possible) region
without the constraint on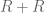 ! (which now is imposed in a relaxed form on
! (which now is imposed in a relaxed form on  ).
).
30 January, 2014 at 9:14 am
Terence Tao
Some sad news: Heini Halberstam, whose conjecture with Peter Elliott (and its generalisations) have been powering all of our recent advances, and who also wrote a seminal textbook on sieve theory with Hans-Egon Richert back in 1974, died last week, aged 87: http://www.news-gazette.com/obituaries/2014-01-27/heini-halberstam.html
30 January, 2014 at 11:54 am
Gergely Harcos
This is sad news indeed. I took his course in 1995 as an undergraduate when I visited UIUC, and he was also very close to me during my graduate studies there from 1996 to 1998. Interestingly, I watched the documentary Nicky’s family (http://www.nickysfamily.com/) a few days ago, and it made me very emotional. I realized Heini Halberstam was among the 669 children saved by the Kindertransport that the movie was about.
30 January, 2014 at 12:58 pm
PD
From wikipedia: “The Kindertransport was a rescue mission that took place during the nine months prior to the outbreak of the Second World War. The United Kingdom took in nearly 10,000 predominantly Jewish children from Nazi Germany, Austria, Czechoslovakia, Poland, and the Free City of Danzig. The children were placed in British foster homes, hostels, schools and farms. Often they were the only members of their families who survived the Holocaust.”
Nicholas Winton (whom this movie is about) found homes for 669 children. “Throughout the summer, he placed advertisements seeking British families to take them in. The last group, which left Prague on 3 September 1939, was sent back because the Nazis had invaded Poland, marking the start of the Second World War.”
30 January, 2014 at 1:38 pm
Gergely Harcos
Thanks for the additional information. In fact Heini Halberstam was among the 669 children saved by Nicholas Winton. See the list at the end of the movie All My Loved Ones (http://www.youtube.com/watch?v=0Ww5PQ8CfMA), at 1:33:00.
30 January, 2014 at 12:52 pm
Fan
Congrats to all working on this problem for getting to 6 on GEH!
Just a comment, is section 1.2 on the wiki page still timeline of the bounds? or is it just notation because the timeline has been moved elsewhere?
[I’ve reorganised the section slightly to clarify this. -T.]
30 January, 2014 at 7:08 pm
Terence Tao
OK, I’ve located the parity barrier again for our new sieves, showing that we cannot prove the twin prime conjecture with the sieves we have (and in particular giving an indirect proof that the answer to Problem 2 is negative; I don’t have a direct proof though). I would imagine that some version of the argument below also blocks any attempt to get , but I haven’t checked this yet.
, but I haven’t checked this yet.
Here are the details (presented somewhat heuristically; also we pretend that everybody is squarefree, otherwise we have to replace the Mobius function with the Liouville function in the discussion below). for some cleverly chosen weights
for some cleverly chosen weights 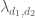 supported on the (generous) region where
supported on the (generous) region where 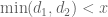 (ignoring epsilon powers of x), and get an upper bound
(ignoring epsilon powers of x), and get an upper bound
To recall: the strategy to prove the twin prime conjecture by these methods would be to build a non-negative sieve
and lower bounds
for which . A key point, to be exploited below, is that we are only “allowed” to use lower bounds (2), (3) that are obtainable from sieve-theoretic methods; in particular the values of
. A key point, to be exploited below, is that we are only “allowed” to use lower bounds (2), (3) that are obtainable from sieve-theoretic methods; in particular the values of 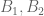 may fall well short of what we believe the true value of the LHS of (2) or (3) to be.
may fall well short of what we believe the true value of the LHS of (2) or (3) to be.
Due to the generous support region, we cannot presume that anticorrelates with
anticorrelates with 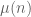 or with
or with  . (For instance,
. (For instance,  is currently an admissible sieve.) However, the constraint
is currently an admissible sieve.) However, the constraint  still gives anticorrelation with
still gives anticorrelation with  :
:
and in particular from (1) we have
up to negligible errors.
Also, the way we would prove (2) relies on distribution hypotheses on the function (the EH conjecture), as well as the non-negativity of this function. Conjecturally, the function
(the EH conjecture), as well as the non-negativity of this function. Conjecturally, the function 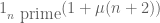 has the same distributional and non-negativity properties as
has the same distributional and non-negativity properties as  , so if we can prove (2) by sieve-theoretic techniques,, we can also prove
, so if we can prove (2) by sieve-theoretic techniques,, we can also prove
which by non-negativity of also implies
also implies
Similarly
and thus on summing
Combining this with (5) we see that , contradiction.
, contradiction.
31 January, 2014 at 2:38 pm
Terence Tao
I looked back at the proof (from https://terrytao.wordpress.com/2014/01/08/polymath8b-v-stretching-the-sieve-support-further/#comment-265206 ) that was not achievable from sieve-theoretic methods and realised that the same proof actually works verbatim for our new sieves too, thus giving another proof of the parity problem obstruction to
was not achievable from sieve-theoretic methods and realised that the same proof actually works verbatim for our new sieves too, thus giving another proof of the parity problem obstruction to  . Basically, any asymptotics we give for a quantity such as
. Basically, any asymptotics we give for a quantity such as 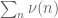 or
or 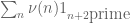 , etc. that can be obtained from sieve-theoretic methods, would also apply if we replaced the constant weight 1 with the weight
, etc. that can be obtained from sieve-theoretic methods, would also apply if we replaced the constant weight 1 with the weight
All the upper and lower bounds we have for quantities such as or
or 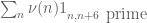 ultimately come from linear combinations of such asymptotics, together with non-negativity of
ultimately come from linear combinations of such asymptotics, together with non-negativity of  . (For instance the “epsilon trick” that gives lower bounds on
. (For instance the “epsilon trick” that gives lower bounds on  falls into this category.) So if these methods could produce
falls into this category.) So if these methods could produce  with the constant weight 1, they should also produce
with the constant weight 1, they should also produce 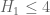 with n weighted by a(n). But by design, for any n in the support of a(n) cannot have n,n+2 both prime, or n+2,n+6 both prime, and so
with n weighted by a(n). But by design, for any n in the support of a(n) cannot have n,n+2 both prime, or n+2,n+6 both prime, and so  cannot be proven sieve-theoretically using the tuple (n,n+2,n+6).
cannot be proven sieve-theoretically using the tuple (n,n+2,n+6).
1 February, 2014 at 2:35 am
Michel Eve
Dear Prof Tao,
If sieve theory cannot prove the twin prime conjecture because of the parity barrer, what other techniques are left in analytic number theory to overcome this barrier ?
1 February, 2014 at 8:18 am
Terence Tao
I discuss this at https://terrytao.wordpress.com/2007/06/05/open-question-the-parity-problem-in-sieve-theory/ . Basically, sieve theory, which is based on linear summation techniques, is known to be insufficient, so the best hope appears to be to somehow convert the twin prime conjecture to a “bilinear” or perhaps even “multilinear” sums problem, and then do … something … to the resulting sums. The problem is that we don’t have a viable candidate for the “something”. On GEH, one can use the Bombieri sieve to convert the twin prime conjecture to the “quartilinear” problem of counting solutions to the equation pq-rs=2, where p,q,r,s are primes (i.e. convert the twin prime problem to a twin semiprime problem). This equation looks tantalisingly susceptible to SL_2-based techniques (e.g. automorphic forms), but we don’t know how to deal with the constraint that p,q,r,s are prime. (The standard technique of Cauchy-Schwarz to eliminate those constraints is insufficient; something else must be done.)
4 February, 2014 at 3:39 am
Chen Wang
For solutions of the twin semiprime problem, could the techniques similar to Chen’s twin prime-semiprime theorem be used?
31 January, 2014 at 11:46 am
Kalpesh Muchhal
Hi, I had a question regarding high k where H=270 has been achieved, whether this can be further lowered conditional on GRH. Since BV controls average error, while GRH does that for individual progressions..is this finer control helpful in the present case..(although with both EH and GRH being conjectures, and EH already giving such great bounds, I now feel the question is somewhat moot :)
31 January, 2014 at 2:34 pm
Terence Tao
I think GRH can be used to get more effective and explicit bounds on the size of the first k-tuple of primes that can be located in a short interval (because the Bombieri-Vinogradov theorem has some ineffectivity in its error terms arising from the possibility of Siegel zeroes), but does not directly impact the size H of that interval. In sieve theory, one is sieving out using a lot of progressions at once, with no single progression causing a significant impact on the sieve, so averaged results such as Bombieri-Vinogradov are what are really of importance in sieve theory; the extra uniformity coming from GRH type hypotheses is only of secondary benefit.
1 February, 2014 at 2:31 am
Kalpesh Muchhal
Thanks Prof. Tao. Speaking of RH, in a future article could you also throw some light on why zeta zeroes and pair correlation concepts haven’t been as fruitful in this area..for example sieves based on sums like sum[pi(x+h) – pi(x)], x between n and 2n, and the prime count function pi estimated using Riemann’s formula, must have been tried and faced some obstacles..
1 February, 2014 at 8:14 am
Terence Tao
Unfortunately, the zeta function appears to be the wrong tool for the job – being essentially Fourier transform of the primes, it captures behaviour of the primes at medium and large scales (particularly if one is willing to average over all values of the position parameter x), but gives significantly less information about the primes at short scales (small values of h). So for instance the RH can give information about primes in [x,x+h] for a single x and h a bit bigger than sqrt(x), or for average x and h bigger than for any fixed
for any fixed 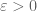 . For twin primes etc., one wants to take h to be bounded, and x in a sparse set (since most short intervals [x,x+h] will not contain even one prime, let alone two), and this is far from the regime in which the zeta function carries information.
. For twin primes etc., one wants to take h to be bounded, and x in a sparse set (since most short intervals [x,x+h] will not contain even one prime, let alone two), and this is far from the regime in which the zeta function carries information.
31 January, 2014 at 10:42 pm
Pace Nielsen
My colleague Roger Baker was wondering if we have a formula to find an explicit k for which (say). I know that Terry found an effectively computable lower bound. Has this been given explicit constants?
(say). I know that Terry found an effectively computable lower bound. Has this been given explicit constants?
31 January, 2014 at 11:11 pm
Terence Tao
In principle this is extractable from http://michaelnielsen.org/polymath1/index.php?title=Selberg_sieve_variational_problem#Lower_bounds , but one has to optimise in a number of additional parameters ( , though in practice we set
, though in practice we set  ). Maple code for this can be found for instance at https://math.mit.edu/~drew/maple_5_BV.txt ; the lower bound for M_k is what is called M0-Delta there, and one can optimise in c and T. (One can ignore the m, varpi, delta variables for the purposes of your particular question.)
). Maple code for this can be found for instance at https://math.mit.edu/~drew/maple_5_BV.txt ; the lower bound for M_k is what is called M0-Delta there, and one can optimise in c and T. (One can ignore the m, varpi, delta variables for the purposes of your particular question.)
1 February, 2014 at 7:08 am
Eytan Paldi
In the notes on the variational problem, it is not clear why the solutions to (0.6), (0.7) should be polynomials.
to (0.6), (0.7) should be polynomials. (i.e.
(i.e. 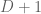 ) and not at most
) and not at most  (as suggested at the end.)
(as suggested at the end.)
Moreover, it seems (by (0.6), (0.7)) that the degrees of these solutions (assuming them to be polynomials) should be at least the degree of
Therefore, I suggest to increase the degrees of these polynomial solutions (at least to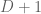 ) and check if (0.6), (0.7) are exactly satisfied by the computed polynomial solutions.
) and check if (0.6), (0.7) are exactly satisfied by the computed polynomial solutions.
1 February, 2014 at 7:17 am
Eytan Paldi
I made a mistake in the degree of (it is
(it is  .)
.)
1 February, 2014 at 8:19 am
Terence Tao
Yes, we have exact solutions which suggest that for polynomial G_0, the functions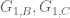 should in fact involve some logarithmic factors, but the hope was that polynomials would serve as a good approximation since one does not expect any singularities here. On the other hand, there may be singularities of some sort within G_0 which are slowing down the analysis.
should in fact involve some logarithmic factors, but the hope was that polynomials would serve as a good approximation since one does not expect any singularities here. On the other hand, there may be singularities of some sort within G_0 which are slowing down the analysis.
1 February, 2014 at 8:19 am
Aubrey de Grey
I’m posting this as a new comment rather than a reply to the relevant comment, just because the chronology of the thread is getting hard to navigate.)
I’ve played with Pace’s latest notebook a little (though I too am a Mathematica novice). First, I’m not succeeding in reproducing Pace’s value of 1.55 for d=13: I get only 1.5279. The convergence is wobbly after d=8, but rather tight – d=7 gives me 1.4940 – so I’m having trouble believing we can progress much more by further increasing d, and even additional partitioning looks quite unpromising.
However, I’ve found something else that might be a clue. I tried to emulate the previous findings arising from exploring changing d just for one partition (or a category of them), and I can’t get ANY change in M from raising the degree that way. I thought I should be able to do this for region A just by replacing “d” by (for example) “10” in the line:
{GMain, AAvars} = SymmPolyGen[x, y, d, AA];
(I can’t see any other place that looks like it would do it) but this has no effect at all on the result. Is this to be expected in this new formulation, or does it indicate a bug?
1 February, 2014 at 9:43 am
Pace Nielsen
Aubrey, the value 1.55 was me trying to remember what the actual value was. [I just remembered M wasn’t bigger than that.] I think 1.5279 is probably correct. Sorry about that confusion.
On the “increasing d” issue, the following is what I’m observing. The vanishing marginal conditions are essentially rewriting each of the polynomial approximations in terms of the others. So, if you increase the degree on the main piece A, then the low degree polynomial approximation on B and C will in turn force most of that degree increase to be worthless.
I currently think that main problem is the symmetry on A. By breaking the symmetry we will have more freedom to choose monomials on (half of) A, and more of this will be compatible with the vanishing marginals.
1 February, 2014 at 11:16 am
Aubrey de Grey
Many thanks for the clarification Pace. If you’re sure that that works to explain the TOTAL lack of impact of changing d for one of the (sets of) partitions, right down to 10^-20, so be it, though that seems odd to me (especially since I see that you only write “force MOST of that degree increase to be worthless”).
Are you saying that you expect a big benefit from dividing A into just two parts, separated by x=y? I would hope that that would not remove too much of the hoped-for advantage of switching from F to G.
1 February, 2014 at 12:33 pm
Pace Nielsen
Yes, I’m pretty sure. But one way to double check it is to do the following. In the code for the “Answer” function, the first line includes a list of local variables.
1. Remove SetOfConditions and SetOfReductions from the list.
2. Run the code with all the same d’s.
3. Then print the SetOfReductions.
4. Run the code with the modified d’s.
5. Print the SetOfReductions again.
If my guess is correct, the new SetOfReductions should include a lot more variables being set to 0. (If you increase degree on the A portion, look for A variables with high numbers being set to 0.)
1 February, 2014 at 8:19 pm
Aubrey de Grey
Yep, that’s what I’m seeing.
Since you already topped 2 with the 3D approach, might it be possible to see the the explicit polynomials and integral outputs for that case, so that Terry can do a Maple computation? Playing a little with the degrees I found that one can stay above M=2 with the U and G degrees being 4 and all the others only 2, which might make this easier. (I find that an epsilon of 2555/10000 does better than 1/4, so there’s no motivation to look at a different partitioning.) Also I’m still curious about the extended prism, since it’s so much bigger than the untruncated simplex; if its M is indeed bigger for a given fixed degree, it might top 2 with even lower degrees.
1 February, 2014 at 9:58 pm
Aubrey de Grey
I just obtained some very surprising behavior while playing more with the degrees in Pace’s 3D notebook. Previously I was keeping the degree of all partitions with the same letter equal, but I tried departing from that and discovered that Gxyz is ridiculously powerful. Setting the degree of Gxyz to 2 and that of absolutely everything else to 1 gives me M=2.046968.
If this is all correct, I hope it will considerably simplify a Maple validation.
1 February, 2014 at 10:35 pm
Aubrey de Grey
Ah… by way of caution in relation to the previous post: I thought I should explore a few other options in order to provide a good “world record”, and I got up to 2.09, but then unfortunately found a set of degrees that gives M=127.93 :-( The set in question is:
Gxyz=5
Gyzx=Gzyx=Uyzx=4
Uxyz=3
Axyz=Cxyz=Sxyz=Hxyz=2
everything else 1
I presume that rather than unveiling a bug in Pace’s code this simply means that stipulating different degrees for components with the same letter is not allowed, thus calling into question my previous finding.
2 February, 2014 at 5:37 am
Pace Nielsen
Aubrey, yes in my code you must stipulate the same degree for the other G-components. As it is set up, this is what ensures that we keep symmetry, and we need symmetry to guarantee that the three J integrals are all equal, etc…
2 February, 2014 at 8:18 am
Aubrey de Grey
Thanks Pace. Just to clarify, however: my initial finding (that one can stay above M=2 with the U and G degrees being 4 and all the others only 2, with possible implications for Maple validation) was not subject to this flaw.
1 February, 2014 at 11:25 am
Terence Tao
I think you’re right about this as the explanation for the slow convergence. The logical thing to do would then be to break A into two pieces, depending on whether or
or 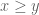 . Unfortunately this creates a “crease” in H on the diagonal, which in turn causes the B and C triangles to be cut in half if one wants to keep them polynomial. Ugh, it’s quite a mess now. (Somehow the 3D partitioning already avoided this problem; it’s still a bit unintuitive to me that the 3D program is performing so much better than the 2D program, but perhaps that’s simply how it is.)
. Unfortunately this creates a “crease” in H on the diagonal, which in turn causes the B and C triangles to be cut in half if one wants to keep them polynomial. Ugh, it’s quite a mess now. (Somehow the 3D partitioning already avoided this problem; it’s still a bit unintuitive to me that the 3D program is performing so much better than the 2D program, but perhaps that’s simply how it is.)
I thought briefly about dropping the symmetry condition altogether, but this would triple (or maybe even sextuple) the number of vanishing marginal conditions and is almost certainly not a win. I’ll try to think if there are any other “cheap” ways to get better convergence here, but we may just have to grit our teeth and partition the 2D polytopes further.
1 February, 2014 at 12:27 pm
Pace Nielsen
I think the intuition on why the 2D problem is performing worse than the 3D problem may be the following. While the 2D version reveals more structure to an optimal solution, the 3D version gives us more room to “decompress” the structure and work on independent pieces.
For instance, in the 3D version the marginal conditions say nothing about the main component. Further, there is a large region (the T region) where the vanishing marginal condition gives only one (very mild) restriction. Thus, there is more freedom to choose polynomials and optimize over these portions of the domain.
In the 2D model, the function’s restrictions to the separate regions are forced to be interdependent, which makes polynomial approximation harder.
2 February, 2014 at 3:04 pm
Pace Nielsen
Aubrey, you asked for explicit polynomials coming from my Mathematica workbook. Here they are (with floating point coefficients) for epsilon=1/4.
FA=1- 1.28813 x + 0.81663 x^2 – 1.30652 y +
0.887704 x y + 1.06809 y^2 – 1.25622 z + 0.643331 x z +
0.447091 y z + 0.835724 z^2
FB=0.557582- 0.615844 x + 0.472821 x^2 – 1.07377 y +
0.448855 x y + 1.03211 y^2 – 0.248981 z – 0.0606339 x z +
0.223752 y z + 0.0916695 z^2
FC=0.340116- 0.657288 x + 0.453068 x^2 – 0.64547 y +
0.581099 x y + 0.511376 y^2 – 0.00929844 z + 0.00330427 x z +
0.0146546 y z + 0.00416013 z^2
FD=0
FE=-2.16828 + 1.88879 x – 1.93478 x^2 – 0.978705 y + 0.294345 x y +
0.546622 y^2 + 5.61586 z + 0.38199 x z + 0.270168 y z – 4.5987 z^2
FG=-263.521 + 1699.78 x – 4784.39 x^2 + 5222.13 x^3 – 1806.61 x^4 +
1154.1 y + 48.4907 x y + 68.5822 x^2 y – 1471.88 x^3 y –
4024.1 y^2 – 503.705 x y^2 + 3235.68 x^2 y^2 + 5031.37 y^3 –
1413.72 x y^3 – 1806.61 y^4 + 630.748 z – 3053.12 x z +
5974.22 x^2 z – 3344.09 x^3 z – 2390.97 y z + 5532.79 y^2 z –
3344.09 y^3 z – 552.712 z^2 + 1788.29 x z^2 – 1848.33 x^2 z^2 +
1633.01 y z^2 – 1891.95 y^2 z^2 + 208.274 z^3 – 338.891 x z^3 –
367.971 y z^3 – 28.0339 z^4
FH=-0.518424 + 2.09666 x – 1.16736 x^2 – 10.9012 y + 5.3936 x y +
11.5925 y^2 + 2.17563 z – 2.38737 x z + 5.2883 y z – 1.22001 z^2
FS=0.0626347+ 1.89748 x – 1.93478 x^2 – 9.76006 y +
0.271189 x y + 6.21113 y^2 + 0.107294 z + 0.370413 x z +
10.8039 y z – 1.22001 z^2
FT=-0.0445971 + 0.069443 x – 0.0264744 x^2 – 0.565025 y + 0.363377 x y +
0.624488 y^2 + 0.35029 z – 0.24018 x z – 0.0110861 y z – 0.213706 z^2
FU=-62.4771 + 759.264 x – 2974.81 x^2 + 4220.43 x^3 – 1806.61 x^4 –
0.816031 y + 8.23017 x y – 61.3701 x^2 y + 130.845 x^3 y –
4.86221 y^2 + 44.7764 x y^2 – 82.771 x^2 y^2 + 3.9055 y^3 –
21.0704 x y^3 + 0.214361 y^4 + 88.709 z – 984.165 x z +
3143.87 x^2 z – 2542.72 x^3 z – 28.088 z^2 +
299.853 x z^2 – 742.184 x^2 z^2 –
2.44422 z^3 + 9.27222 x z^3 – 0.0428723 z^4
2 February, 2014 at 8:04 pm
Aubrey de Grey
Many thanks Pace. (I presume you confirmed an M of 2.0000395 for this set of degrees.) Even though this reduces the number of coefficients by 40% relative to the degree set you used to get 2.0009, there are still 132 of them, which I’m guessing is quite laborious to code in Maple (something that I’m afraid I have no idea how to do). I suppose the question is whether there is any cheaper way than that to obtain satisfactory confirmation of H_1=6 and allow focus to return to the unconditional setting. The extended prism might be the only other option, but of course there’s work involved in creating the Mathematica code and it’s a complete guess whether it would deliver less complexity.
3 February, 2014 at 12:31 pm
Terence Tao
Thanks for this! I should be able to confirm that this works in Maple, though I might not get around to it for a few days as there are several other things on my plate right now. If you could post your values for I and J for this choice of coefficients that would help for the confirmation purposes. (One nice thing is that once one actually has the explicit description of F, it doesn’t really matter where it came from or what exactly it was optimising; one can simply compute the ratio J/I and check that it exceeds 2. So one doesn’t have to confirm all of the numerical optimisation, one just has to check the answer that comes out at the end.)
3 February, 2014 at 12:56 pm
Pace Nielsen
Even with these explicit polynomials I think this will still be complicated, but good luck!
My values for the I and J integrals are (respectively) 0.0306247, 0.0612506.
9 February, 2014 at 3:13 pm
Terence Tao
Finally have some spare time to compute the I and J integrals. I am getting 0.03062203133 for the I integral (computed in a slightly different way from in your notes), but this might possibly be due to the roundoff coming from the use of decimals instead of fractions. Do you have a version of FA-FH with rational (or maybe integer) coefficients (clearing denominators if necessary)?
For sake of checking, here are the individual I integrals I am getting:
I(A)= 0.003405849935
I(B)= 0.0008483246927
I(C)= 0.0008209224485
I(D)= 0
I(E)= 0.4684111483 10^-5
I(S)=0.7034444492 10^-6
I(T)=0.2366227122 10^-5
I(U)=0.8858487383 10^-5
I(G)=0.7143129988 10^-5
I(H)=0.4819411681 10^-5
I was hoping to use Maple’s Heaviside function to perform the integrals, but in practice I found that Maple can really only handle one Heaviside function at a time (and occasionally two), which allowed me to compute some, but not all, of the integrals directly.
I also computed the volumes of the various polytopes as a further checksum:
A = 27/1536
B = 26/1536
C = 55/1536
D = 8/1536
E = 1/1536
F = 22/1536
S = 2/1536
T = 16/1536
U = 4/1536
G = 4/1536
H = 1/1536
everything adds up as expected.
I’ll turn to the J integrals next, of course, then the vanishing marginal conditions. Here I don’t see any shortcuts other than to simply repeat what is in your notes, but I’ll try to check the integral formulae while doing so.
eps:=1/4;
Axyz:=Heaviside((1-eps)-(z+x));
Dxyz:=Heaviside(1+eps-(z+x))*Heaviside((x+y)-(1-eps));
ABCDxyz:=Heaviside(1+eps-(z+x));
ABExyz:=Heaviside((1-eps)-(y+z));
Exyz:=Heaviside((z+x)-(1+eps))*Heaviside((1-eps)-(y+z));
BExyz := ABExyz - Axyz;
Bxyz:=ABExyz-Axyz-Exyz;
Gxyz:=Heaviside(y+z-(1+eps));
DHxyz:=Heaviside(x+y-(1-eps));
CFxyz:=Heaviside((y+z)-(1-eps))-DHxyz-Gxyz;
Hxyz:=DHxyz-Dxyz;
Fxyz:=CFxyz-Cxyz;
FA:=1-1.28813*x+0.8166*x^2-1.30652*y+0.887704*x*y+1.06809*y^2-1.25622*z+0.643331*x*z+0.447091*y*z+0.835724*z^2;
FB:=0.557582-0.615844*x+0.472821*x^2-1.07377*y+0.448855*x*y+1.03211*y^2-0.248981*z-0.0606339*x*z+0.223752*y*z+0.0916695*z^2;
FC:=0.340116-0.657288*x+0.453068*x^2-0.64547*y+0.581099*x*y+0.511376*y^2-0.00929844*z+0.00330427*x*z+0.0146546*y*z+0.00416013*z^2;
FD:=0
FE:=-2.16828+1.88879*x-1.93478*x^2-0.978705*y+0.294345*x*y+0.546622*y^2+5.61586*z+0.38199*x*z+0.270168*y*z-4.5987*z^2;
FG:=-263.521+1699.78*x-4784.39*x^2+5222.13*x^3-1806.61*x^4+1154.1*y+48.4907*x*y+68.5822*x^2*y-1471.88*x^3*y-4024.1*y^2-
503.705*x*y^2+3235.68*x^2*y^2+5031.37*y^3-1413.72*x*y^3-1806.61*y^4+630.748*z-3053.12*x*z+5974.22*x^2*z-3344.09*x^3*z-2390.97*y*z+5532.79*y^2*z-
3344.09*y^3*z-552.712*z^2+1788.29*x*z^2-1848.33*x^2*z^2+1633.01*y*z^2-1891.95*y^2*z^2+208.274*z^3-338.891*x*z^3-367.971*y*z^3-28.0339*z^4;
FH:=-0.518424+2.09666*x-1.16736*x^2-10.9012*y+5.3936*x*y+11.5925*y^2+2.17563*z-2.38737*x*z+5.2883*y*z-1.22001*z^2;
FS:=0.0626347+1.89748*x-1.93478*x^2-9.76006*y+0.271189*x*y+6.21113*y^2+0.107294*z+0.370413*x*z+10.8039*y*z-1.22001*z^2;
FT:=-0.0445971+0.069443*x-0.0264744*x^2-0.565025*y+0.363377*x*y+0.624488*y^2+0.35029*z-0.24018*x*z-0.0110861*y*z-0.213706*z^2;
FU:=-62.4771+759.264*x-2974.81*x^2+4220.43*x^3-1806.61*x^4-0.816031*y+8.23017*x*y-61.3701*x^2*y+130.845*x^3*y-4.86221*y^2+44.7764*x*y^2-
82.771*x^2*y^2+3.9055*y^3-21.0704*x*y^3+0.214361*y^4+88.709*z-984.165*x*z+3143.87*x^2*z-2542.72*x^3*z-28.088*z^2+299.853*x*z^2-742.184*x^2*z^2-
2.44422*z^3+9.27222*x*z^3-0.0428723*z^4;
IA := int(int(int(FA*FA*Axyz,z=x..(3/2-y-x)),x=y..(3/2-y)/2),y=0..1/2);
# 0.003405849935
IB := int(int(int(FB*FB*BExyz,z=x..(3/2-y-x)),x=y..(3/2-y)/2),y=0..1/2) - int(int(int(FB*FB,y=0..1-eps-z),x=1+eps-z..z),z=1/2+eps/2..1-eps);
# 0.0008483246927
IC := int(int(int(FC*FC*ABCDxyz,z=x..(3/2-y-x)),x=y..(3/2-y)/2),y=0..1/2) - int(int(int(FC*FC*Axyz,z=x..(3/2-y-x)),x=y..(3/2-y)/2),y=0..1/2) - int(int(int
(FC*FC*BExyz,z=x..(3/2-y-x)),x=y..(3/2-y)/2),y=0..1/2) - int(int(int(FC*FC*Dxyz,z=x..(3/2-y-x)),x=y..(3/2-y)/2),y=0..1/2) + int(int(int(FC*FC,y=0..1-
eps-z),x=1+eps-z..z),z=1/2+eps/2..1-eps);
# 0.0008209224485
ID := int(int(int(FD*FD*Dxyz,z=x..(3/2-y-x)),x=y..(3/2-y)/2),y=0..1/2);
# 0
IE := int(int(int(FE*FE,y=0..1-eps-z),x=1+eps-z..z),z=1/2+eps/2..1-eps);
# 0.4684111483 10^-5
IS := int(int(int(FS*FS,x=1+eps-z..(1-eps-y)),z=y+2*eps..1/2+eps),y=1/2-3*eps/2..1/2-eps)+int(int(int(FS*FS,x=1+eps-z..(1-eps-y)),z=1-eps-
y..1/2+eps),y=0..1/2-3*eps/2);
# 0.7034444492 10^-6
IT := int(int(int(FT*FT,y=0..3/2-x-z),x=1/2-eps..3/2-z),z=1/2+2*eps..1+eps)+int(int(int(FT*FT,y=0..3/2-x-z),x=1+eps-z..3/2-z),z=1/2+eps..1/2+2*eps);
# 0.2366227122 10^-5
IU := int(int(int(FU*FU,z=1+eps-x..1+eps-y),y=0..x),x=0..1/2-eps);
# 0.8858487383 10^-5
IG := int(int(int(FG*FG*Gxyz,z=x..(3/2-y-x)),x=y..(3/2-y)/2),y=0..1/2);
# 0.7143129988 10^-5
IH := int(int(int(FH*FH*Hxyz,z=x..(3/2-y-x)),x=y..(3/2-y)/2),y=0..1/2);
# 0.4819411681 10^-5
Isum := 6*(IA+IB+IC+ID+IE+IS+IT+IU+IG+IH);
9 February, 2014 at 3:42 pm
Aubrey de Grey
I quickly proofread the Maple code and found only one typo, which I’m not sure would explain the discrepancy: the second coefficient in FA is missing its last digit (0.8166, should be 0.81663).
9 February, 2014 at 4:33 pm
Terence Tao
Well spotted! This increases the I-value to 0.03062212678 (I(A) increases to 0.003405865844). So this doesn’t explain the entire discrepancy…
9 February, 2014 at 4:46 pm
Pace Nielsen
Here are the numbers I get:
I(A)=0.003405880062
I(B)=0.0008483272329
I(C)=0.0008209190117
I(D)=0
I(E)=4.684618094*10^-6
I(S)=7.034678581*10^-7
I(T)=2.366234915*10^-6
I(U)=8.881367920*10^-6
I(G)=7.535069959*10^-6
I(H)=4.820553682*10^-6
These seem to all match extremely well, except the U and G pieces. (This makes a lot of sense as you’ll see below that the U and G pieces should have a lot of round-off error since they involve more of the variables.)
—————–
I’m going to copy and paste some variables and fractions and hopefully you can just copy these into your code. (If this doesn’t work, I’ll make the file available tomorrow when I get to work.)
The variables are:
{AA1, AA10, AA2, AA3, AA4, AA5, AA6, AA7, AA8, AA9, BB1, BB10, BB2, BB3, BB4, BB5, BB6, BB7, BB8, BB9, CC1, CC10, CC2, CC3, CC4, CC5, CC6, CC7, CC8, CC9, EE4, EE6, EE7, EE9, HH9, SS10, SS3, SS4, SS6, SS7, SS8, SS9, TT4, TT7, TT8, TT9, UU16, UU18, UU2, UU20, UU21, UU22, UU23, UU24, UU25, UU26, UU27, UU28, UU29, UU3, UU30, UU31, UU4, UU5, UU6, UU7, UU8, UU9}
The values to be plugged in for these variables are:
{1, 1045142938208869499191181851782774507/\
1250583557010555646667061395704693241, -(
316190143410376180877743423449314379/
245464443795540077818629001202004919), -(
1891769024614429265911454167348900079/
1447939476712835671464363817808062688), -(
6645228840627884543963048543908513027/
5289876174681743792060084416381005195), \
339382475899332801872344573142712540/\
382315024741410006634197807400450109, \
800533017763591087028889327164205386/\
1244356905396458217205005409940313975, \
610227319942583521343573321987866901/\
1364882503730947175994072119119099314, \
889358636648145697618963860699826673/\
1089059167005007839552742646367084883, \
1129697701772130766129061623987627555/\
1057677648341105966172642014701620358, \
369411148833963466416948486507827637/\
662523432040271503868922466512394931, \
70036650704097962432270211642055587/\
764012880419651000309703978698201099, -(
1560220310742393302871638104929376767/
2533466855538622711494072790849524188), -(
675291956550121180518604625359119746/
628900966577543384705927335762397661), -(
2529381695462699016828722243204952689/
10158934785795031265990553206322976713), \
301473130543012653915144253204794977/\
671648655006425274620020662289591135, -(
72843967588099728726005521157785775/
1201374210126871248100329027582696868), \
143825707895572733498873732281838861/\
642792029730168691317286168208033538, \
649120491616113171860687738354432093/\
1372868684761191246523483175495609470, \
923204127144474133750324575031071970/\
894483138835109750336516244948229253, \
504054606061804606346982706190041169/\
1482009696315178162834773520112425988, \
6393539409569434525570984945744351/\
1536858786446366256984445263822713064, -(
790669890434879790226924633515000611/
1202927660436616925000852487643859754), -(
583951140942993837488005058061406582/
904691553133220160159156823559029957), -(
22155783335807716384604672631876769/
2382741655599610617339893240473178207), \
861834403869460514116581559993754859/\
1483110658557996492977375659547372425, \
1929146726486743959255980765537648/\
583834071458801022674364752868975235, \
21780572077072279546180172035622479/\
1486260981903228631659801660491854709, \
184535211848461345418175814435319135/\
407301027098512230853641880451245568, \
232080145073024378344663228214923163/\
453834445204584035710168200740458909, \
5472538654920722429742789691613843676/\
974479232954197975340589995394266455, \
927222828149050158923800771583485723/\
2427346765941624985384346616239603038, \
250517508328910949894678249652185722/\
927265216411134102504733935734045705, \
1240108547818177956234040673419197568/\
2268677602592314368751160380697174029, \
9405819102419059244834716575963924175/\
811372333735457494738136754843943653, -(
1432088304215654669021352650864060725/
1173831359938549301293098635807566287), -(
11612115950284073971150222762767416620/
1189758425639212572034398845328452639), \
103937977558232440508940501348834518/\
968720338025380091790884725502334715, \
214224468539246347682035898225657185/\
578340038314441580717115396074382778, \
16011015326505338708151388841891253041/\
1481970237969351533821283886719874867, -(
2152329004242745879844194442185193763/
1112441007795743584614598777366749922), \
8652296470217515560135397830496043201/\
1393032063270399805786566196554189095, \
2724262739331687731618153452386489771/\
7777163575787859138926611143971853064, -(
3533612330801100162685856352893683/
318742786972619370533192728831094789), -(
8634152014937802133186289083541939/
326132136552676474614615351931787892), \
639258673765815764176758921945001459/\
1023652233362766137377498777586011863, 0, -(
1036177365908403576222625465669165224191/
1396118752614173365815190752515315262), \
683163754447358515357759652655917657307/\
899770442732486890915132953316493212, \
3977430161340892036145546371180618658240/\
942423718900792196615855892814714641, \
4369967465028547394227392689218793956/\
1118925727402664937850908867587807095, -(
6493264317462327139909085594207259201/
2656583931468774802084917498666106861), \
208533806588523947204108028241851658601/\
1593749576650909843879153107097169586, -(
2586867413257547105405021630653379594931/
1017361494191501491128242008483670506), -(
46075356336908979453982139912989909769/
2186736965136790998934152365709299888), \
21583120699474906684881271067473540892/\
2327719037190114284507554697536132109, 0, 0, -(
4493884950736564857307858442065834123411/
2487469455179284947187381390582168137), -(
912131634231853063945020626889013945/
1117765710674185487041664983420906397), \
385418773588866232850515087462213507/\
1797985734299399330339559894335414707, -(
60846714782262228976526525072918278/
1419255270556600115075698318707631525), \
38086532340155117976291869658511569399/\
429342259347747976339594153498728242, \
9900518239375432526911040812620204965/\
1202954557712616339652022357371972894, -(
1363826261161475275558885344800775294047/
1385770492279731028804032285608964254), 0, -(
3986739775635725156458528972312106107630/
1340165793339507490854268037177642059), -(
2967616495233435231968510933124363413/
610343298456544672866212720080088296)}
The explicit polynomials are:
FA= AA1 + AA2 x + AA8 x^2 + AA3 y + AA5 x y + AA9 y^2 + AA4 z + AA6 x z + AA7 y z + AA10 z^2
FB= BB1 + BB2 x + BB8 x^2 + BB3 y + BB5 x y + BB9 y^2 + BB4 z + BB6 x z + BB7 y z + BB10 z^2
FC= CC1 + CC2 x + CC8 x^2 + CC3 y + CC5 x y + CC9 y^2 + CC4 z + CC6 x z + CC7 y z + CC10 z^2
FE= -((3 EE4)/4) – (9 EE7)/32 + (3 EE9)/16 – (9 SS10)/16 – (3 SS3)/8 – ( 3 SS9)/8 + (-((3 EE6)/4) + SS3/2 + (3 SS7)/8 – (3 SS8)/4 + SS9/4) x + SS8 x^2 + (2 EE4 + (3 EE7)/4 – EE9 + SS3 – 2 SS4 – (3 SS7)/4 +
SS9) y + (2 EE6 – 2 SS6 + 2 SS8 + (2 SS9)/3) x y + EE9 y^2 +
EE4 z + EE6 x z + EE7 y z + (EE7/2 – EE9/3 + SS10 – SS7/2 + SS9/3) z^2
FS= -((9 SS10)/16) – (3 SS3)/8 – (3 SS4)/4 – (9 SS7)/32 – (
3 SS9)/16 + (SS3/2 – (3 SS6)/4 + (3 SS7)/8 – (3 SS8)/4 + SS9/4) x +
SS8 x^2 + SS3 y + (2 SS8 + (2 SS9)/3) x y + SS9 y^2 + SS4 z +
SS6 x z + SS7 y z + SS10 z^2
FT = -((3 TT4)/2) – (9 TT7)/8 + (
3 TT9)/4 + (TT4 + (3 TT7)/4 – (3 TT8)/2 – TT9/2) x +
TT8 x^2 + (2 TT4 + (3 TT7)/2 – 2 TT9) y + (2 TT8 + (2 TT9)/3) x y +
TT9 y^2 + TT4 z + (TT7/2 + TT8 – TT9/3) x z +
TT7 y z + (TT7/2 – TT9/3) z^2
FU= -((125 UU16)/256) – UU2/16 + UU20/512 + (125 UU22)/128 + (
5 UU23)/8192 + (5 UU24)/4096 + (125 UU26)/2048 – (
625 UU28)/1024 + UU29/1280 – (5 UU3)/16 + (625 UU31)/256 – (
5 UU4)/8 – (5 UU5)/256 – (5 UU6)/128 – (25 UU7)/64 + UU2 x +
UU8 x^2 + UU20 x^3 + UU29 x^4 + UU3 y +
UU5 x y + (-((225 UU16)/26) + (5 UU18)/2 – (24 UU2)/5 + (333 UU20)/
260 + (225 UU21)/26 + (225 UU22)/13 – (423 UU23)/832 + (
1089 UU24)/416 + (45 UU25)/16 – (105 UU26)/16 – (1125 UU28)/
104 – (3 UU29)/25 + (72 UU3)/13 + (225 UU30)/26 + (1125 UU31)/
26 – (144 UU4)/13 – (3 UU5)/2 – 3 UU6 – (90 UU7)/13 – (8 UU8)/
5 + (120 UU9)/13) x^2 y + UU23 x^3 y +
UU9 y^2 + ((165 UU16)/26 – (27 UU20)/52 – (165 UU21)/26 – (165 UU22)/
13 – (75 UU23)/416 – (15 UU24)/52 – (69 UU25)/80 – (87 UU26)/
40 + (825 UU28)/104 – (27 UU29)/25 – (264 UU3)/65 – (165 UU30)/
26 – (825 UU31)/26 + (528 UU4)/65 – (3 UU5)/5 + (6 UU6)/5 + (
66 UU7)/13 – (88 UU9)/13) x y^2 + (-3 UU18 + (81 UU23)/80 – (
81 UU24)/40 – (147 UU25)/40 + (147 UU26)/10 + (108 UU29)/
25) x^2 y^2 + UU21 y^3 + UU25 x y^3 + UU30 y^4 + UU4 z +
UU6 x z + ((225 UU16)/52 – (5 UU18)/4 – (12 UU2)/5 – (567 UU20)/
520 – (225 UU21)/52 – (225 UU22)/26 + (189 UU23)/1664 – (
1323 UU24)/832 – (45 UU25)/32 + (255 UU26)/32 + (1125 UU28)/
208 – (3 UU29)/50 – (36 UU3)/13 – (225 UU30)/52 – (1125 UU31)/
52 + (72 UU4)/13 – (3 UU5)/4 – (3 UU6)/2 + (45 UU7)/13 – (4 UU8)/
5 – (60 UU9)/13) x^2 z + UU24 x^3 z +
UU7 y z + ((3 UU16)/2 + (3 UU21)/4 – 3 UU22 + (3 UU25)/16 – (3 UU26)/
4 – (15 UU27)/16 + (15 UU28)/8 + (3 UU30)/2 – (15 UU31)/2) y^2 z +
UU27 y^3 z + ((5 UU16)/13 – (3 UU20)/208 – (15 UU21)/208 – (
105 UU22)/52 + (5 UU23)/3328 – (35 UU24)/1664 – (3 UU25)/128 + (
3 UU26)/32 + (25 UU28)/52 + (2 UU3)/13 – (15 UU30)/208 – (
725 UU31)/208 – (4 UU4)/13 + (4 UU7)/13 – UU9/
13) z^2 + (-((15 UU16)/13) + (3 UU20)/13 + (15 UU21)/13 + (
30 UU22)/13 – (63 UU23)/2080 + (363 UU24)/1040 + (3 UU25)/8 – (
27 UU26)/8 – (75 UU28)/52 + (48 UU3)/65 + (15 UU30)/13 + (
75 UU31)/13 – (96 UU4)/65 + UU5/5 – (2 UU6)/5 – (12 UU7)/13 + (
16 UU9)/13) x z^2 + UU18 x^2 z^2 +
UU16 y z^2 + ((3 UU27)/4 + (3 UU28)/2 – (3 UU30)/5 –
3 UU31) y^2 z^2 + UU22 z^3 + UU26 x z^3 + UU28 y z^3 + UU31 z^4
FG= -((9 UU2)/4) + (27 UU20)/64 + (513 UU23)/2048 + (27 UU24)/1024 – (
243 UU25)/512 + (2097 UU26)/512 + (153 UU29)/160 – (45 UU5)/64 – (
45 UU6)/32 + (6 UU2 – (99 UU23)/256 + (99 UU24)/128 + (99 UU25)/
64 – (771 UU26)/64 – (33 UU29)/20 + (15 UU5)/8 + (15 UU6)/
4) x + (-3 UU2 – (27 UU20)/16 – (117 UU23)/512 – (423 UU24)/
256 – (153 UU25)/128 + (987 UU26)/128 + (33 UU29)/40 – (15 UU5)/
16 – (15 UU6)/8) x^2 + (UU20 + UU23/4 + (3 UU24)/4 + UU25/4 –
UU26 – (8 UU29)/5) x^3 +
UU29 x^4 + (-((675 UU16)/104) + 6 UU2 – (81 UU20)/208 + (675 UU21)/
104 + (675 UU22)/52 – (8919 UU23)/16640 + (4869 UU24)/8320 + (
369 UU25)/160 – (4827 UU26)/320 – (3375 UU28)/416 – (123 UU29)/
50 + (54 UU3)/13 + (675 UU30)/104 + (3375 UU31)/104 – (108 UU4)/
13 + (15 UU5)/8 + (15 UU6)/4 – (135 UU7)/26 + (90 UU9)/13) y + ((
225 UU16)/13 – 8 UU2 – (45 UU20)/13 – (225 UU21)/13 – (450 UU22)/
13 + (1929 UU23)/4160 – (10929 UU24)/2080 – (453 UU25)/80 + (
2437 UU26)/80 + (1125 UU28)/52 + UU29/25 – (144 UU3)/13 – (
225 UU30)/13 – (1125 UU31)/13 + (288 UU4)/13 – (5 UU5)/2 –
5 UU6 + (180 UU7)/13 – (240 UU9)/13) x y + (-((225 UU16)/26) + (
207 UU20)/52 + (225 UU21)/26 + (225 UU22)/13 – (441 UU23)/1040 + (
6057 UU24)/1040 + (243 UU25)/80 – (243 UU26)/20 – (1125 UU28)/
104 + (9 UU29)/25 + (72 UU3)/13 + (225 UU30)/26 + (1125 UU31)/
26 – (144 UU4)/13 – (90 UU7)/13 + (120 UU9)/13) x^2 y + ((3 UU23)/
5 – (6 UU24)/5 – (2 UU25)/5 + (8 UU26)/5 + (64 UU29)/
25) x^3 y + ((225 UU16)/26 – 3 UU2 – (243 UU20)/208 – (225 UU21)/
26 – (225 UU22)/13 – (981 UU23)/33280 – (23319 UU24)/16640 – (
1773 UU25)/640 + (8967 UU26)/640 + (1125 UU28)/104 + (381 UU29)/
200 – (72 UU3)/13 – (225 UU30)/26 – (1125 UU31)/26 + (144 UU4)/
13 – (15 UU5)/16 – (15 UU6)/8 + (90 UU7)/13 – (120 UU9)/
13) y^2 + (-((375 UU16)/26) + (189 UU20)/52 + (375 UU21)/26 + (
375 UU22)/13 – (579 UU23)/1040 + (5883 UU24)/1040 + (417 UU25)/
80 – (417 UU26)/20 – (1875 UU28)/104 – (9 UU29)/25 + (120 UU3)/
13 + (375 UU30)/26 + (1875 UU31)/26 – (240 UU4)/13 – (150 UU7)/
13 + (200 UU9)/13) x y^2 + ((27 UU23)/20 – (27 UU24)/10 – (
33 UU25)/20 + (33 UU26)/5 + (54 UU29)/
25) x^2 y^2 + (-((25 UU16)/13) + (23 UU20)/26 + (25 UU21)/13 + (
50 UU22)/13 + (107 UU23)/520 + (361 UU24)/520 + (39 UU25)/40 – (
39 UU26)/10 – (125 UU28)/52 – (46 UU29)/25 + (16 UU3)/13 + (
25 UU30)/13 + (125 UU31)/13 – (32 UU4)/13 – (20 UU7)/13 + (
80 UU9)/39) y^3 + ((3 UU23)/5 – (6 UU24)/5 – (7 UU25)/5 + (
28 UU26)/5 + (64 UU29)/25) x y^3 +
UU29 y^4 + ((675 UU16)/208 + 3 UU2 – (621 UU20)/416 – (675 UU21)/
208 – (675 UU22)/104 – (20799 UU23)/33280 – (10251 UU24)/16640 + (
99 UU25)/320 – (2667 UU26)/640 + (3375 UU28)/832 – (129 UU29)/
50 – (27 UU3)/13 – (675 UU30)/208 – (3375 UU31)/208 + (54 UU4)/
13 + (15 UU5)/16 + (15 UU6)/8 + (135 UU7)/52 – (45 UU9)/
13) z + (-((225 UU16)/26) – 4 UU2 + (45 UU20)/26 + (225 UU21)/
26 + (225 UU22)/13 + (5169 UU23)/8320 + (3831 UU24)/4160 – (
93 UU25)/160 + (997 UU26)/160 – (1125 UU28)/104 + (181 UU29)/
50 + (72 UU3)/13 + (225 UU30)/26 + (1125 UU31)/26 – (144 UU4)/
13 – (5 UU5)/4 – (5 UU6)/2 – (90 UU7)/13 + (120 UU9)/13) x z + ((
225 UU16)/52 + (27 UU20)/104 – (225 UU21)/52 – (225 UU22)/26 + (
909 UU23)/2080 – (1143 UU24)/2080 + (63 UU25)/160 – (63 UU26)/
40 + (1125 UU28)/208 – (81 UU29)/50 – (36 UU3)/13 – (225 UU30)/
52 – (1125 UU31)/52 + (72 UU4)/13 + (45 UU7)/13 – (60 UU9)/
13) x^2 z + (-(UU23/5) + (2 UU24)/5 – UU25/5 + (4 UU26)/5 + (
32 UU29)/25) x^3 z + (-4 UU2 + (9 UU20)/4 + (105 UU23)/128 + (
75 UU24)/64 – (15 UU25)/32 + (185 UU26)/32 + (47 UU29)/10 – (
5 UU5)/4 – (5 UU6)/2) y z + (-((75 UU16)/52) – (9 UU20)/104 + (
75 UU21)/52 + (75 UU22)/26 + (633 UU23)/2080 – (1491 UU24)/
2080 + (51 UU25)/160 – (51 UU26)/40 – (375 UU28)/208 – (117 UU29)/
50 + (12 UU3)/13 + (75 UU30)/52 + (375 UU31)/52 – (24 UU4)/13 – (
15 UU7)/13 + (20 UU9)/13) y^2 z + (-(UU23/5) + (2 UU24)/5 – UU25/
5 + (4 UU26)/5 + (32 UU29)/25) y^3 z + (-((225 UU16)/52) – UU2 + (
297 UU20)/208 + (225 UU21)/52 + (225 UU22)/26 + (21297 UU23)/
33280 + (8403 UU24)/16640 – (39 UU25)/640 + (781 UU26)/640 – (
1125 UU28)/208 + (523 UU29)/200 + (36 UU3)/13 + (225 UU30)/52 + (
1125 UU31)/52 – (72 UU4)/13 – (5 UU5)/16 – (5 UU6)/8 – (45 UU7)/
13 + (60 UU9)/13) z^2 + ((75 UU16)/13 – (15 UU20)/13 – (75 UU21)/
13 – (150 UU22)/13 – (243 UU23)/520 – (33 UU24)/65 + (3 UU25)/
5 – (12 UU26)/5 + (375 UU28)/52 – (66 UU29)/25 – (48 UU3)/13 – (
75 UU30)/13 – (375 UU31)/13 + (96 UU4)/13 + (60 UU7)/13 – (
80 UU9)/13) x z^2 + (-((9 UU23)/80) + (9 UU24)/40 – (27 UU25)/
40 + (27 UU26)/10 + (18 UU29)/25) x^2 z^2 + ((75 UU16)/26 – (
69 UU20)/52 – (75 UU21)/26 – (75 UU22)/13 – (111 UU23)/208 – (
123 UU24)/208 – (9 UU25)/16 + (9 UU26)/4 + (375 UU28)/104 –
3 UU29 – (24 UU3)/13 – (75 UU30)/26 – (375 UU31)/26 + (48 UU4)/
13 + (30 UU7)/13 – (40 UU9)/13) y z^2 + (-((9 UU23)/80) + (
9 UU24)/40 + (3 UU25)/40 – (3 UU26)/10 + (18 UU29)/
25) y^2 z^2 + ((75 UU16)/52 – (43 UU20)/104 – (75 UU21)/52 – (
75 UU22)/26 – (659 UU23)/2080 + (243 UU24)/2080 + (37 UU25)/
160 – (37 UU26)/40 + (375 UU28)/208 – (59 UU29)/50 – (12 UU3)/
13 – (75 UU30)/52 – (375 UU31)/52 + (24 UU4)/13 + (15 UU7)/13 – (
20 UU9)/13) z^3 + ((3 UU23)/20 – (3 UU24)/10 – (3 UU25)/5 + (
12 UU26)/5 + (16 UU29)/25) x z^3 + ((3 UU23)/20 – (3 UU24)/10 –
UU25/10 + (2 UU26)/5 + (16 UU29)/25) y z^3 + (UU23/16 – UU24/8 –
UU25/8 + UU26/2 + UU29/5) z^4
FH= (3 HH9)/8 – (9 SS10)/8 – (3 SS4)/2 – (
9 SS7)/16 + (-((3 HH9)/4) + (3 SS10)/4 + SS4 – (3 SS6)/2 + (9 SS7)/
8) x + (HH9/3 + SS6 – SS7/2) x^2 + (-((3 HH9)/2) + (3 SS10)/2 +
2 SS4 + (3 SS7)/4) y + ((4 HH9)/3 + 2 SS6 – SS7) x y +
HH9 y^2 + (-(HH9/4) – (3 SS10)/4 + SS4 + (3 SS7)/8) z + (HH9/3 +
SS10 + SS6 – SS7/2) x z + ((2 HH9)/3 + 2 SS10) y z + SS10 z^2
9 February, 2014 at 5:19 pm
Terence Tao
I computed the J sum to be 0.06142977105 (using the decimal data with Aubrey’s correction; I just saw the rational values but have not yet input them). This is close to what you have (in fact, my ratio is somewhat better), but the numerical discrepancy is a little troubling. Here is the breakdown:
J1 = 0.005366492245
J2 = 0.0002247808601
J3 = 0.002180015009
J4 = 0.0001510339809
J5 = 0.001311833953
J6 = 0.0004372898451
J7 = 0.0003343819451
J8 = 0.0002324673362
I have not yet verified the formulae for the J integrals; I am going to do that next.
(the code below should be run after the previous set of code).
FAxyz := FA;
FAyzx := subs( {x=y,y=z,z=x}, FA );
FAzyx := subs( {x=z,z=x}, FA );
FBxyz := FB;
FByzx := subs( {x=y,y=z,z=x}, FB );
FBzyx := subs( {x=z,z=x}, FB );
FCxyz := FC;
FCyzx := subs( {x=y,y=z,z=x}, FC );
FCzyx := subs( {x=z,z=x}, FC );
FExyz := FE;
FEyzx := subs( {x=y,y=z,z=x}, FE );
FEzyx := subs( {x=z,z=x}, FE );
FSxyz := FS;
FSyzx := subs( {x=y,y=z,z=x}, FS );
FSzyx := subs( {x=z,z=x}, FS );
FTxyz := FT;
FTyzx := subs( {x=y,y=z,z=x}, FT );
FTzyx := subs( {x=z,z=x}, FT );
FUxyz := FU;
FUyzx := subs( {x=y,y=z,z=x}, FU );
FUzyx := subs( {x=z,z=x}, FU );
FGxyz := FG;
FGyzx := subs( {x=y,y=z,z=x}, FG );
FGzyx := subs( {x=z,z=x}, FG );
FHxyz := FH;
FHyzx := subs( {x=y,y=z,z=x}, FH );
FHzyx := subs( {x=z,z=x}, FH );
J1func := int(FAyzx, z=0..y) + int(FAzyx, z=y..x) + int(FAxyz, z=x..1-eps-x) + int(FBxyz, z=1-eps-x..1-eps-y) + int(FCxyz, z=1-eps-y..1+eps-x) + int(FUxyz, z=1+eps-x..1+eps-y) + int(FGxyz, z=1+eps-y..3/2-x-y);
J1 := int(int(J1func*J1func, y=0..x), x=0..1/2-eps);
J2func := int(FAyzx, z=0..y) + int(FAzyx, z=y..x) + int(FAxyz, z=x..1-eps-x) + int(FBxyz, z=1-eps-x..1-eps-y) + int(FCxyz, z=1-eps-y..3/2-x-y);
J2 := int(int(J2func*J2func, y=1/2-eps..x),x=1/2-eps..1/2-eps/2);
J3func := int(FAyzx, z=0..y) + int(FAzyx, z=y..x) + int(FAxyz, z=x..1-eps-x) + int(FBxyz, z=1-eps-x..1-eps-y) + int(FCxyz, z=1-eps-y..1+eps-x) + int(FTxyz, z=1+eps-x..3/2-x-y);
J3 := int(int(J3func*J3func, y=0..1/2-eps),x=1/2-eps..1/2-eps/2);
J4func := int(FAyzx, z=0..y) + int(FAzyx, z=y..1-eps-x) + int(FBzyx, z=1-eps-x..x) + int(FBxyz, z=x..1-eps-y) + int(FCxyz, z=1-eps-y..3/2-x-y);
J4 := int(int(J4func*J4func, y=1/2-eps..1-eps-x), x=1/2-eps/2..1/2);
J5func := int(FAyzx, z=0..y) + int(FAzyx, z=y..1-eps-x) + int(FBzyx, z=1-eps-x..x) + int(FBxyz, z=x..1-eps-y) + int(FCxyz, z=1-eps-y..1+eps-x) + int(FTxyz, z=1+eps-x..3/2-x-y);
J5 := int(int(J5func*J5func,y=0..1/2-eps),x=1/2-eps/2..1/2);
J6func := int(FAyzx, z=0..y) + int(FAzyx, z=y..1-eps-x) + int(FBzyx, z=1-eps-x..x) + int(FBxyz, z=x..1-eps-y) + int(FCxyz, z=1-eps-y..1+eps-x) + int(FSxyz, z=1+eps-x..1/2+eps) + int(FTxyz, z=1/2+eps..3/2-x-y);
J6 := int(int(J6func*J6func,y=x-2*eps..1-eps-x),x=2*eps..1/2+eps/2) + int(int(J6func*J6func,y=0..1-eps-x),x=1/2..2*eps);
J7func := int(FAyzx, z=0..y) + int(FAzyx, z=y..1-eps-x) + int(FBzyx, z=1-eps-x..x) + int(FBxyz, z=x..1-eps-y) + int(FExyz, z=1+eps-x..1-eps-y) + int(FSxyz, z=1-eps-y..1/2+eps) + int(FTxyz, z=1/2+eps..3/2-x-y);
J7 := int(int(J7func*J7func,y=0..x-2*eps),x=2*eps..1/2+eps/2);
J8func := int(FAyzx, z=0..y) + int(FAzyx, z=y..1-eps-x) + int(FBzyx, z=1-eps-x..1+eps-x) + int(FEzyx, z=1+eps-x..x) + int(FExyz, z=x..1-eps-y) + int(FSxyz, z=1-eps-y..1/2+eps) + int(FTxyz, z=1/2+eps..3/2-x-y);
J8 := int(int(J8func*J8func,y=0..1-eps-x),x=1/2+eps/2..1-eps);
Jsum := 6*(J1+J2+J3+J4+J5+J6+J7+J8);
9 February, 2014 at 5:40 pm
Pace Nielsen
Here are the values I get for the various J integral parts:
J1= 0.005361969338
J2= 0.0002247811682
J3= 0.002180020663
J4= 0.0001510347099
J5= 0.001311839873
J6= 0.0004372914519
J7= 0.0003090305213
J8= 0.0002324692288
The only one that doesn’t match well is the J7 component. (Looking at your code, I believe that the integral on Bxyz should have a different upper limit.)
9 February, 2014 at 7:53 pm
Terence Tao
Thanks for checking! I now get J7 = 0.0003090289458 and J=0.06127746389. So J-2I is about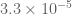 , which is barely one order of magnitude above all the rounding errors we are seeing here – but presumably when we switch to the precise rational coefficients, this will no longer be a problem.
, which is barely one order of magnitude above all the rounding errors we are seeing here – but presumably when we switch to the precise rational coefficients, this will no longer be a problem.
I did check (rather tediously) that all the limits of integration in the J integrals appear to be correct (other than my typo that you caught). Next step will be entering the precise rational data, then checking the marginals, and then we can call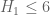 on GEH confirmed. :-)
on GEH confirmed. :-)
9 February, 2014 at 8:00 pm
Pace Nielsen
Excellent! As you noted, the integrals get quite tedious so it is good to get a double check on that computation. Thank you for doing that.
9 February, 2014 at 9:38 pm
Terence Tao
With the rational values, I match your I and J integrals exactly! More precisely, I have
I = 0.03062470572 and J = 0.06125062172 (which are also enormous rational numbers). I put the code at
http://michaelnielsen.org/polymath1/index.php?title=Notes_on_polytope_decomposition#Code
Last thing to do now is to check the marginals…
9 February, 2014 at 10:34 pm
Terence Tao
Good news – the marginals check out, and I also verified the range of integrations for the marginals. Actually, in the eps=1/4 case it looks like the M6 and M8 conditions are not needed, so one might possibly be able to get better/cleaner numbers and/or lower degrees by removing these conditions.
Anyway… I’m now listing H_1=6 on GEH as confirmed! If this were a physical collaboration, I’d pop the champagne about now, but we’ll have to content ourselves with virtual bubbly here. ;-)
4 February, 2014 at 3:05 pm
Eytan Paldi
Rigorous confirmation using piecewise polynomial which does not satisfy the marginal condition:
Let be a vector representing (in some fixed order) the coefficients of a piecewise polynomial
be a vector representing (in some fixed order) the coefficients of a piecewise polynomial  .
.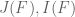 can be represented by
can be represented by
The quadratic functionals
(1)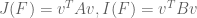
where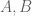 are fixed, positive semi-definite matrices.
are fixed, positive semi-definite matrices.
Similarly, the marginal constraints can be represented by
(2)
where is a fixed, full-rank matrix.
is a fixed, full-rank matrix.
In order to confirm a solution to problem 1, we need to show the existence of a (representing) vector which satisfy (2) and
which satisfy (2) and
(3)
Now suppose that a vector is given which satisfy (3) but not (2). The problem is to use this (approximate) information to show the existence of
is given which satisfy (3) but not (2). The problem is to use this (approximate) information to show the existence of  satisfying both (2) and (3).
satisfying both (2) and (3).
The natural choice for is to take the projection of
is to take the projection of  on the subspace satisfying (2), i.e
on the subspace satisfying (2), i.e
(4)
Note that (automatically) satisfy (2), we need only to verify that it satisfy also (3). Since
(automatically) satisfy (2), we need only to verify that it satisfy also (3). Since
The confirmation of (3) follows provided that we have a sufficiently small upper bound on .
.
3 February, 2014 at 12:51 pm
Eytan Paldi
For a rigorous confirmation, the coefficients should be given as rational numbers (to satisfy the marginal vanishing constraints!)
3 February, 2014 at 1:28 pm
Pace Nielsen
True, but the fractions that arise are not suited to copy and pasting to this blog. One should be able to at least test whether the marginals get extremely close to zero.
3 February, 2014 at 2:05 pm
Eytan Paldi
The problem is with the numerical sensitivity (i.e. how one knows that by slightly perturbing the coefficients in order to satisfy the constraints, the ratio still stays above 2 ?)
1 February, 2014 at 8:52 am
Eytan Paldi
This reminds me that in a previous comment (related to slow convergence) it was observed that certain coefficients were enforced to be zero (indicating significant loss in the remaining degrees of freedom.)
2 February, 2014 at 4:13 pm
interested non-expert
Hello! I wonder what the next step of this project is now, after Pace Nielsen’s code gave H_1<=6 and Terence Tao showed that this sieve can not get H_1<=4 (both on GEH). Is the next step expanding the result without (G)EH assumtion or are you trying to get a new sieve which might go beyond H_1<=4? Thanks and good luck :-)
3 February, 2014 at 9:44 am
Terence Tao
I’m beginning to incline to the view that we might soon declare victory on the Polymath8b project, even though the headline bound of 270 may still have some room for improvement. Initially, the hope was to use the Polymath8a results to improve these bounds, but (except for the m >= 2 results) the progress has instead proceeded in a slightly different direction, through advances in the sieves used and in the numerics. There are actually quite a lot of technical innovations that go into the Polymath8b results already in this regard, and it would make a sizeable paper (not quite as large as the Polymath8a behemoth, but still pretty big). Trying to also tack on Polymath8a type results (in particular, the tentative improvement to MPZ that requires some nontrivial algebraic geometry facts that have yet to be verified) may simply be too much for a single paper. So perhaps after we verify the H_1=6 results, and see if there are any “cheap” ways to push the 270 down further, we may just write up what we have. (There could always be a Polymath8c, of course; and, given recent history, there could also be a surprising new breakthrough coming from outside Polymath.)
3 February, 2014 at 11:36 am
Aubrey de Grey
Makes sense. An alternative might be to write up the [G]EH work and the unconditional work as separate papers – is that worth considering? The two papers might not be written at the same time, I guess – maybe the GEH setting may be felt to have reached a natural victory-declaring point but the unconditional setting not?
Since it’s been a while since the unconditional setting was discussed, there may be value in refreshing our memory by briefly collecting together the ideas that seemed to offer opportunities for cheap progress beyond H_1=270. Here’s what I can recall; am I missing anything?
1) Increasing theta from 0.5 to the polymath8a equivalent of 0.524 or so, as noted. If the current upper bounds of M and M’ are any guide, this might reduce k by as much as 10.
2) The epsilon trick. Seems like its impact will decay rather fast with k, but it’s too soon to say how fast, since it hasn’t been tried with two-digit k for any domain.
3) Exploring higher-degree F. On current evidence it’s looking, however, as though there’s very little more to squeeze here; my guess is that, for k of current interest, degrees of 25 and infinity will deliver k differing by at most 1.
4) Extending the domain of F from R to R’. The known upper bounds for M and M’ imply that k might fall by about 3 if methods used to get to k=54 are adapted to M’. I’m not clear whether there are currently any obstacles to this avenue.
5) Further extending the domain to some version of R’’. Even though the impact of extending R’ to R’’ fell short of initial expectations for small k, this could be a bigger win for two-digit k since the ratio of volumes is so much bigger (in particular, the simplex of size 2 is so huge that the extra volume arising from the prisms that comprise R+R may not even be worth considering). I think Eytan suggested that this might at least halve k.
Avenue (5) would seem to be the most promising quantitatively, but it could be the most challenging computationally. I believe there are two alternatives so far raised to the presumably-totally-impractical option of dissecting the polytope as with k=3:
– the method Terry outlined in https://terrytao.wordpress.com/2013/12/20/polymath8b-iv-enlarging-the-sieve-support-more-efficient-numerics-and-explicit-asymptotics/#comment-258264 . However, Pace noted that even this is likely to be combinatorially challenging as k rises.
– the grid-point scheme proposed by polikimre in https://terrytao.wordpress.com/2014/01/28/polymath8b-vii-using-the-generalised-elliott-halberstam-hypothesis-to-enlarge-the-sieve-support-yet-further/#comment-268675 – but maybe the computations are daunting there too. In that regard might it be worth looking at grids of hybrid granularity – coarser for coordinates further from the R’’ boundary?
3 February, 2014 at 3:09 pm
Aubrey de Grey
A couple of small followups relating to computational complexity:
– In https://terrytao.wordpress.com/2014/01/08/polymath8b-v-stretching-the-sieve-support-further/#comment-263500 Terry provided a “cheap scaling trick” for incorporating epsilon after F has already been chosen, but as far as I can see Pace is instead calculating F with epsilon already specified. I’m unclear as to the status of Terry’s trick – and, in particular, whether it can be applied for larger R or larger k. If it can, could it provide a significant efficiency saving?
– A trick that Pace is indeed using for k=3 is to restrict the monomials of F to have only two dimensions with non-zero exponents, taking advantage of the calculus-of-variations observation that allowed F to be converted to G. This has turned out to be of only modest utility for k=3, because the key goal was reached with only low-degree polynomials – but does it also work for larger k? In https://terrytao.wordpress.com/2014/01/08/polymath8b-v-stretching-the-sieve-support-further/#comment-264256 Terry explained that one cannot iterate on this idea with k=3, but even restricting to monomials with at most k-1 dimensions represented could be a significant efficiency win if the degree is being allowed to rise into two digits.
3 February, 2014 at 4:10 pm
Eytan Paldi
Another possibility is to use the largest possible (as described in a previous, comment – 30 January, 5:11 pm). The idea is to get rid of the
(as described in a previous, comment – 30 January, 5:11 pm). The idea is to get rid of the 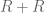 constraint by replacing it with a weaker constraint on
constraint by replacing it with a weaker constraint on  (which is automatically satisfied for this largest
(which is automatically satisfied for this largest  .) Unfortunately, there is no response yet to the potential use of this large
.) Unfortunately, there is no response yet to the potential use of this large  .
.
3 February, 2014 at 5:03 pm
Aubrey de Grey
Ah yes. Is that essentially equivalent to the “free boundary problem” idea that Terry mentioned in https://terrytao.wordpress.com/2014/01/17/polymath8b-vi-a-low-dimensional-variational-problem/#comment-267880 ?
3 February, 2014 at 5:22 pm
Eytan Paldi
Perhaps it looks similar, but the idea here (as confirmed by Terry to my previous question) is that the constraint on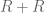 is not really needed but a (weaker) constraint on
is not really needed but a (weaker) constraint on  is what really needed!
is what really needed! automatically holds by choosing the above largest
automatically holds by choosing the above largest  (without satisfying the original constraint on
(without satisfying the original constraint on 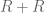 – which is no more needed for this large
– which is no more needed for this large  !)
!)
It follows that the latter constraint on
3 February, 2014 at 5:45 pm
Aubrey de Grey
Going further back, Terry also offered a couple of other ideas back before Christmas for expanding the domain in https://terrytao.wordpress.com/2013/12/20/polymath8b-iv-enlarging-the-sieve-support-more-efficient-numerics-and-explicit-asymptotics/#comment-258637 – so there seems to be no shortage of options in that regard. However, I have no idea to what extent those older ideas are obviated by more recent ones such as the epsilon trick.
3 February, 2014 at 6:26 pm
Eytan Paldi
Yes. but note that this large seems to be the largest possible (since it is the region containing
seems to be the largest possible (since it is the region containing 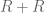 – according to the current “too strong” constraint on
– according to the current “too strong” constraint on 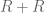 .)
.)
3 February, 2014 at 8:04 pm
Aubrey de Grey
Sure – it’s just that it remains to be seen whether there are greater difficulties in computing with that choice than with others.
4 February, 2014 at 7:35 am
arch1
Building on the hybrid grid notion, I wonder whether in some scenarios it could be useful to change grid size as a function not only of space but also of time, in order to radically reduce expected # of processor cycles relative to a static grid.
6 February, 2014 at 9:44 pm
Gil Kalai
Here is a question of a more general type. Selberg’s beautiful original application for his sieve was to give an upper bound for the number of k-tuples of primes of the form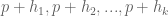 and this upper bound was
and this upper bound was 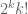 (or so) times the Hardy-Littlewood conjecture. Are the new methods developed recently capable of improving this bound, even based on conjectures like EH or GEH? Incidently what is a good self-contained place to read about Selberg’s original application?
(or so) times the Hardy-Littlewood conjecture. Are the new methods developed recently capable of improving this bound, even based on conjectures like EH or GEH? Incidently what is a good self-contained place to read about Selberg’s original application?
7 February, 2014 at 4:24 pm
Terence Tao
This is a good question! Here’s what I think the situation is with the most general sieve we have: the count for prime k-tuples given by a sieve with cutoff function F overshoots the expected number predicted by the prime tuples conjecture by the quantity
and in particular if F is the indicator function of a region R (which is the optimal case given that F is supported on R), the overshoot is the reciprocal of the volume of R.
Now, the constraints on R are that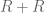 lies in the union of the simplex
lies in the union of the simplex
and the prisms
where is the level of distribution (1/2 from BV, or 1 if one assumes GEH).
is the level of distribution (1/2 from BV, or 1 if one assumes GEH).
Selberg’s original argument, in this language, amounts to taking R to be the simplex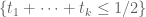 , which has volume
, which has volume  , explaining the overshoot by
, explaining the overshoot by  . One can also take the prism
. One can also take the prism  , which has volume
, which has volume  , giving an overshoot of
, giving an overshoot of  ; I think this bound was already known in the literature (one uses a k-1-dimensional Selberg sieve weighted by
; I think this bound was already known in the literature (one uses a k-1-dimensional Selberg sieve weighted by  ), though I don’t know of an explicit reference (the k=2 case is in Montgomery-Vaughan’s book though). We can take the simplex
), though I don’t know of an explicit reference (the k=2 case is in Montgomery-Vaughan’s book though). We can take the simplex 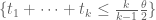 , but this gives an inferior result even on GEH, namely
, but this gives an inferior result even on GEH, namely  . There might be other choices of R that beat the prism, but I can’t think of one right now.
. There might be other choices of R that beat the prism, but I can’t think of one right now.
7 February, 2014 at 9:09 am
“New equidistribution estimates of Zhang type, and bounded gaps between primes” – and a retrospective | What's new
[…] paper) to a fresh thread. (Discussion of the ongoing Polymath8b project is however being kept on a separate thread, to try to reduce […]
9 February, 2014 at 10:57 pm
Polymath8b, VIII: Time to start writing up the results? | What's new
[…] for small values of (in particular ) or asymptotically as . The previous thread may be found here. The currently best known bounds on can be found at the wiki […]
24 October, 2017 at 6:28 pm
Computers, Mathematics, and Complexity – Think Mathematics
[…] current best research tells us that there are infinitely many primes that differ by at most six. This was established […]