Discretised wave equations

The wave equation is usually expressed in the form

where is a function of both time and space , with being the Laplacian operator. One can generalise this equation in a number of ways, for instance by replacing the spatial domain with some other manifold and replacing the Laplacian with the Laplace-Beltrami operator or adding lower order terms (such as a potential, or a coupling with a magnetic field). But for sake of discussion let us work with the classical wave equation on . We will work formally in this post, being unconcerned with issues of convergence, justifying interchange of integrals, derivatives, or limits, etc.. One then has a conserved energy

which we can rewrite using integration by parts and the inner product on as

A key feature of the wave equation is finite speed of propagation: if, at time (say), the initial position and initial velocity are both supported in a ball , then at any later time , the position and velocity are supported in the larger ball . This can be seen for instance (formally, at least) by inspecting the exterior energy

and observing (after some integration by parts and differentiation under the integral sign) that it is non-increasing in time, non-negative, and vanishing at time .

The wave equation is second order in time, but one can turn it into a first order system by working with the pair rather than just the single field , where is the velocity field. The system is then

and the conserved energy is now

Finite speed of propagation then tells us that if are both supported on , then are supported on for all . One also has time reversal symmetry: if is a solution, then is a solution also, thus for instance one can establish an analogue of finite speed of propagation for negative times using this symmetry.

If one has an eigenfunction

of the Laplacian, then we have the explicit solutions

of the wave equation, which formally can be used to construct all other solutions via the principle of superposition.

When one has vanishing initial velocity , the solution is given via functional calculus by

and the propagator can be expressed as the average of half-wave operators:

One can view as a minor of the full wave propagator

which is unitary with respect to the energy form (1), and is the fundamental solution to the wave equation in the sense that

Viewing the contraction as a minor of a unitary operator is an instance of the “dilation trick“.

It turns out (as I learned from Yuval Peres) that there is a useful discrete analogue of the wave equation (and of all of the above facts), in which the time variable now lives on the integers rather than on , and the spatial domain can be replaced by discrete domains also (such as graphs). Formally, the system is now of the form

where is now an integer, take values in some Hilbert space (e.g. functions on a graph ), and is some operator on that Hilbert space (which in applications will usually be a self-adjoint contraction). To connect this with the classical wave equation, let us first consider a rescaling of this system

where is a small parameter (representing the discretised time step), now takes values in the integer multiples of , and is the wave propagator operator or the heat propagator (the two operators are different, but agree to fourth order in ). One can then formally verify that the wave equation emerges from this rescaled system in the limit . (Thus, is not exactly the direct analogue of the Laplacian , but can be viewed as something like in the case of small , or if we are not rescaling to the small case. The operator is sometimes known as the diffusion operator)

Assuming is self-adjoint, solutions to the system (3) formally conserve the energy

This energy is positive semi-definite if is a contraction. We have the same time reversal symmetry as before: if solves the system (3), then so does . If one has an eigenfunction

to the operator , then one has an explicit solution

to (3), and (in principle at least) this generates all other solutions via the principle of superposition.

Finite speed of propagation is a lot easier in the discrete setting, though one has to offset the support of the “velocity” field by one unit. Suppose we know that has unit speed in the sense that whenever is supported in a ball , then is supported in the ball . Then an easy induction shows that if are supported in respectively, then are supported in .

The fundamental solution to the discretised wave equation (3), in the sense of (2), is given by the formula

where and are the Chebyshev polynomials of the first and second kind, thus

and

In particular, is now a minor of , and can also be viewed as an average of with its inverse :

As before, is unitary with respect to the energy form (4), so this is another instance of the dilation trick in action. The powers and are discrete analogues of the heat propagators and wave propagators respectively.

One nice application of all this formalism, which I learned from Yuval Peres, is the Varopoulos-Carne inequality:

Theorem 1 (Varopoulos-Carne inequality) Let be a (possibly infinite) regular graph, let , and let be vertices in . Then the probability that the simple random walk at lands at at time is at most , where is the graph distance.

This general inequality is quite sharp, as one can see using the standard Cayley graph on the integers . Very roughly speaking, it asserts that on a regular graph of reasonably controlled growth (e.g. polynomial growth), random walks of length concentrate on the ball of radius or so centred at the origin of the random walk.

Proof: Let be the graph Laplacian, thus

for any , where is the degree of the regular graph and sum is over the vertices that are adjacent to . This is a contraction of unit speed, and the probability that the random walk at lands at at time is

where are the Dirac deltas at . Using (5), we can rewrite this as

where we are now using the energy form (4). We can write

where is the simple random walk of length on the integers, that is to say where are independent uniform Bernoulli signs. Thus we wish to show that

By finite speed of propagation, the inner product here vanishes if . For we can use Cauchy-Schwarz and the unitary nature of to bound the inner product by . Thus the left-hand side may be upper bounded by

and the claim now follows from the Chernoff inequality.

This inequality has many applications, particularly with regards to relating the entropy, mixing time, and concentration of random walks with volume growth of balls; see this text of Lyons and Peres for some examples.

For sake of comparison, here is a continuous counterpart to the Varopoulos-Carne inequality:

Theorem 2 (Continuous Varopoulos-Carne inequality) Let , and let be supported on compact sets respectively. Then

where is the Euclidean distance between and .

Proof: By Fourier inversion one has

for any real , and thus

By finite speed of propagation, the inner product vanishes when ; otherwise, we can use Cauchy-Schwarz and the contractive nature of to bound this inner product by . Thus

Bounding by , we obtain the claim.

Observe that the argument is quite general and can be applied for instance to other Riemannian manifolds than .

Cayley graphs and the algebra of groups

This is a sequel to my previous blog post “Cayley graphs and the geometry of groups“. In that post, the concept of a Cayley graph of a group was used to place some geometry on that group . In this post, we explore a variant of that theme, in which (fragments of) a Cayley graph on is used to describe the basic algebraic structure of , and in particular on elementary word identities in . Readers who are familiar with either category theory or group homology/cohomology will recognise these concepts lurking not far beneath the surface; we wil remark briefly on these connections later in this post. However, no knowledge of categories or cohomology is needed for the main discussion, which is primarily focused on elementary group theory.

Throughout this post, we fix a single group , which is allowed to be non-abelian and/or infinite. All our graphs will be directed, with loops and multiple edges permitted.

In the previous post, we drew the entire Cayley graph of a group . Here, we will be working much more locally, and will only draw the portions of the Cayley graph that are relevant to the discussion. In this graph, the vertices are elements of the group , and one draws a directed edge from to labeled (or “coloured”) by the group element for any ; the graph consisting of all such vertices and edges will be denoted . 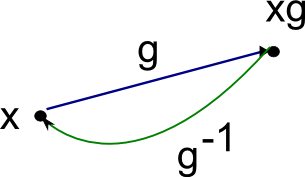Thus, a typical edge in looks like this:

Figure 1.

One usually does not work with the complete Cayley graph . It is customary to instead work with smaller Cayley graphs , in which the edge colours are restricted to a smaller subset of , such as a set of generators for . As we will be working locally, we will in fact work with even smaller fragments of at a time; in particular, we only use a handful of colours (no more than nine, in fact, for any given diagram), and we will not require these colours to generate the entire group (we do not care if the Cayley graph is connected or not, as this is a global property rather than a local one).

Cayley graphs are left-invariant: for any , the left translation map is a graph isomorphism. To emphasise this left invariance, we will usually omit the vertex labels, and leave only the coloured directed edge, like so:

Figure 2.

This is analogous to how, in undergraduate mathematics and physics, vectors in Euclidean space are often depicted as arrows of a given magnitude and direction, with the initial and final points of this arrow being of secondary importance only. (Indeed, this depiction of vectors in a vector space can be viewed as an abelian special case of the more general depiction of group elements used in this post.)

Let us define a diagram to be a finite directed graph , with edges coloured by elements of , which has at least one graph homomorphism into the complete Cayley graph of ; thus there exists a map (not necessarily injective) with the property that whenever is a directed edge in coloured by a group element . Informally, a diagram is a finite subgraph of a Cayley graph with the vertex labels omitted, and with distinct vertices permitted to represent the same group element. Thus, for instance, the single directed edge displayed in Figure 2 is a very simple example of a diagram. An even simpler example of a diagram would be a depiction of the identity element:

Figure 3.

We will however omit the identity loops in our diagrams in order to reduce clutter.

We make the obvious remark that any directed edge in a diagram can be coloured by at most one group element , since implies . This simple observation provides a way to prove group theoretic identities using diagrams: to show that two group elements are equal, it suffices to show that they connect together (with the same orientation) the same pair of vertices in a diagram.

Remark 1 One can also interpret these diagrams as commutative diagrams in a category in which all the objects are copies of , and the morphisms are right-translation maps. However, we will deviate somewhat from the category theoretic way of thinking here by focusing on the geometric arrangement and shape of these diagrams, rather than on their abstract combinatorial description. In particular, we view the arrows more as distorted analogues of vector arrows, than as the abstract arrows appearing in category theory.

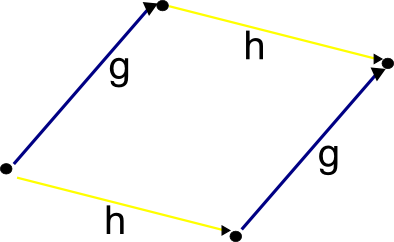
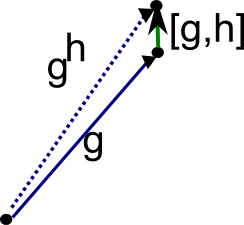
Just as vector addition can be expressed via concatenation of arrows, group multiplication can be described by concatenation of directed edges. Indeed, for any , the vertices can be connected by the following triangular diagram:

Figure 4.

In a similar spirit, inversion is described by the following diagram:

Figure 5.

We make the pedantic remark though that we do not consider a edge to be the reversal of the edge, but rather as a distinct edge that just happens to have the same initial and final endpoints as the reversal of the edge. (This will be of minor importance later, when we start integrating “-forms” on such edges.)

A fundamental operation for us will be that of gluing two diagrams together.

Lemma 1 ((Labeled) gluing) Let be two diagrams of a given group . Suppose that the intersection of the two diagrams connects all of (i.e. any two elements of are joined by a path in ). Then the union is also a diagram of .

Proof: By hypothesis, we have graph homomorphisms , . If they agree on then one simply glues together the two homomorphisms to create a new graph homomorphism . If they do not agree, one can apply a left translation to either or to make the two diagrams agree on at least one vertex of ; then by the connected nature of we see that they now must agree on all vertices of , and then we can form the glued graph homomorphism as before.

The above lemma required one to specify the label the vertices of (in order to form the intersection and union ). However, if one is presented with two diagrams with unlabeled vertices, one can identify some partial set of vertices of with a partial set of vertices of of matching cardinality. Provided that the subdiagram common to and after this identification connects all of the common vertices together, we may use the above lemma to create a glued diagram .

For instance, if a diagram contains two of the three edges in the triangular diagram in Figure 4, one can “fill in” the triangle by gluing in the third edge:

Figure 6.

One can use glued diagrams to demonstrate various basic group-theoretic identities. For instance, by gluing together two copies of the triangular diagram in Figure 4 to create the glued diagram

Figure 7.

and then filling in two more triangles, we obtain a tetrahedral diagram that demonstrates the associative law :

Figure 8.

Similarly, by gluing together two copies of Figure 4 with three copies of Figure 5 in an appropriate order, we can demonstrate the Abel identity :

Figure 9.

In addition to gluing, we will also use the trivial operation of erasing: if is a diagram for a group , then any subgraph of (formed by removing vertices and/or edges) is also a diagram of . This operation is not strictly necessary for our applications, but serves to reduce clutter in the pictures.

If two group elements commute, then we obtain a parallelogram as a diagram, exactly as in the vector space case:

Figure 10.

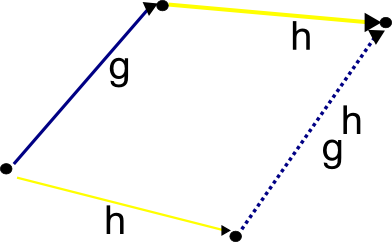
In general, of course, two arbitrary group elements will fail to commute, and so this parallelogram is no longer available. However, various substitutes for this diagram exist. For instance, if we introduce the conjugate of one group element by another, then we have the following slightly distorted parallelogram:

Figure 11.

By appropriate gluing and filling, this can be used to demonstrate the homomorphism properties of a conjugation map :

Figure 12.

Figure 13.

Another way to replace the parallelogram in Figure 10 is to introduce the commutator of two elements, in which case we can perturb the parallelogram into a pentagon:

Figure 14.

We will tend to depict commutator edges as being somewhat shorter than the edges generating that commutator, reflecting a “perturbative” or “nilpotent” philosophy. (Of course, to fully reflect a nilpotent perspective, one should orient commutator edges in a different dimension from their generating edges, but of course the diagrams drawn here do not have enough dimensions to display this perspective easily.) We will also be adopting a “Lie” perspective of interpreting groups as behaving like perturbations of vector spaces, in particular by trying to draw all edges of the same colour as being approximately (though not perfectly) parallel to each other (and with approximately the same length).

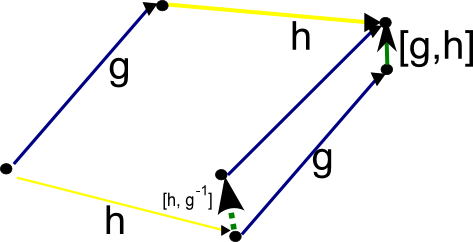
Gluing the above pentagon with the conjugation parallelogram and erasing some edges, we discover a “commutator-conjugate” triangle, describing the basic identity :

Figure 15.

Other gluings can also give the basic relations between commutators and conjugates. For instance, by gluing the pentagon in Figure 14 with its reflection, we see that . The following diagram, obtained by gluing together copies of Figures 11 and 15, demonstrates that ,

Figure 16.

while this figure demonstrates that :

Figure 17.

Now we turn to a more sophisticated identity, the Hall-Witt identity

which is the fully noncommutative version of the more well-known Jacobi identity for Lie algebras.

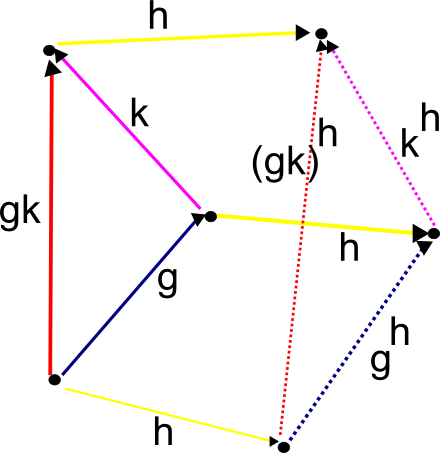
The full diagram for the Hall-Witt identity resembles a slightly truncated parallelopiped. Drawing this truncated paralleopiped in full would result in a rather complicated looking diagram, so I will instead display three components of this diagram separately, and leave it to the reader to mentally glue these three components back to form the full parallelopiped. The first component of the diagram is formed by gluing together three pentagons from Figure 14, and looks like this:

Figure 18.

This should be thought of as the “back” of the truncated parallelopiped needed to establish the Hall-Witt identity.

While it is not needed for proving the Hall-Witt identity, we also observe for future reference that we may also glue in some distorted parallelograms and obtain a slightly more complicated diagram:

Figure 19.

To form the second component, let us now erase all interior components of Figure 18 or Figure 19:

Figure 20.

Then we fill in three distorted parallelograms:

Figure 21.

This is the second component, and is the “front” of the truncated praallelopiped, minus the portions exposed by the truncation.

Finally, we turn to the third component. We begin by erasing the outer edges from the second component in Figure 21:

Figure 22.

We glue in three copies of the commutator-conjugate triangle from Figure 15:

Figure 23.

But now we observe that we can fill in three pentagons, and obtain a small triangle with edges :

Figure 24.

Erasing everything except this triangle gives the Hall-Witt identity. Alternatively, one can glue together Figures 18, 21, and 24 to obtain a truncated parallelopiped which one can view as a geometric representation of the proof of the Hall-Witt identity.

Among other things, I found these diagrams to be useful to visualise group cohomology; I give a simple example of this below, developing an analogue of the Hall-Witt identity for -cocycles.

254B, Notes 7: Sieving and expanders

In this final set of course notes, we discuss how (a generalisation of) the expansion results obtained in the preceding notes can be used for some number-theoretic applications, and in particular to locate almost primes inside orbits of thin groups, following the work of Bourgain, Gamburd, and Sarnak. We will not attempt here to obtain the sharpest or most general results in this direction, but instead focus on the simplest instances of these results which are still illustrative of the ideas involved.

One of the basic general problems in analytic number theory is to locate tuples of primes of a certain form; for instance, the famous (and still unsolved) twin prime conjecture asserts that there are infinitely many pairs in the line in which both entries are prime. In a similar spirit, one of the Landau conjectures (also still unsolved) asserts that there are infinitely many primes in the set . The Mersenne prime conjecture (also unsolved) asserts that there are infinitely many primes in the set , and so forth.

More generally, given some explicit subset in (or , if one wishes), such as an algebraic variety, one can ask the question of whether there are infinitely many integer lattice points in in which all the coefficients are simultaneously prime; let us refer to such points as prime points.

At this level of generality, this problem is impossibly difficult. Indeed, even the much simpler problem of deciding whether the set is non-empty (let alone containing prime points) when is a hypersurface cut out by a polynomial is essentially Hilbert’s tenth problem, which is known to be undecidable in general by Matiyasevich’s theorem. So one needs to restrict attention to a more special class of sets , in which the question of finding integer points is not so difficult. One model case is to consider orbits , where is a fixed lattice vector and is some discrete group that acts on somehow (e.g. might be embedded as a subgroup of the special linear group , or on the affine group ). In such a situation it is then quite easy to show that is large; for instance, will be infinite precisely when the stabiliser of in has infinite index in .

Even in this simpler setting, the question of determining whether an orbit contains infinitely prime points is still extremely difficult; indeed the three examples given above of the twin prime conjecture, Landau conjecture, and Mersenne prime conjecture are essentially of this form (possibly after some slight modification of the underlying ring , see this paper of Bourgain-Gamburd-Sarnak for details), and are all unsolved (and generally considered well out of reach of current technology). Indeed, the list of non-trivial orbits which are known to contain infinitely many prime points is quite slim; Euclid’s theorem on the infinitude of primes handles the case , Dirichlet’s theorem handles infinite arithmetic progressions , and a somewhat complicated result of Green, Tao, and Ziegler handles “non-degenerate” affine lattices in of rank two or more (such as the lattice of length arithmetic progressions), but there are few other positive results known that are not based on the above cases (though we will note the remarkable theorem of Friedlander and Iwaniec that there are infinitely many primes of the form , and the related result of Heath-Brown that there are infinitely many primes of the form , as being in a kindred spirit to the above results, though they are not explicitly associated to an orbit of a reasonable action as far as I know).

On the other hand, much more is known if one is willing to replace the primes by the larger set of almost primes – integers with a small number of prime factors (counting multiplicity). Specifically, for any , let us call an -almost prime an integer which is the product of at most primes, and possibly by the unit as well. Many of the above sorts of questions which are open for primes, are known for -almost primes for sufficiently large. For instance, with regards to the twin prime conjecture, it is a result of Chen that there are infinitely many pairs where is a prime and is a -almost prime; in a similar vein, it is a result of Iwaniec that there are infinitely many -almost primes of the form . On the other hand, it is still open for any fixed whether there are infinitely many Mersenne numbers which are -almost primes. (For the superficially similar situation with the numbers , it is in fact believed (but again unproven) that there are only finitely many -almost primes for any fixed (the Fermat prime conjecture).)

The main tool that allows one to count almost primes in orbits is sieve theory. The reason for this lies in the simple observation that in order to ensure that an integer of magnitude at most is an -almost prime, it suffices to guarantee that is not divisible by any prime less than . Thus, to create -almost primes, one can start with the integers up to some large threshold and remove (or “sieve out”) all the integers that are multiples of any prime less than . The difficulty is then to ensure that a sufficiently non-trivial quantity of integers remain after this process, for the purposes of finding points in the given set .

The most basic sieve of this form is the sieve of Eratosthenes, which when combined with the inclusion-exclusion principle gives the Legendre sieve (or exact sieve), which gives an exact formula for quantities such as the number of natural numbers less than or equal to that are not divisible by any prime less than or equal to a given threshold . Unfortunately, when one tries to evaluate this formula, one encounters error terms which grow exponentially in , rendering this sieve useful only for very small thresholds (of logarithmic size in ). To improve the sieve level up to a small power of such as , one has to replace the exact sieve by upper bound sieves and lower bound sieves which only seek to obtain upper or lower bounds on quantities such as , but contain a polynomial number of terms rather than an exponential number. There are a variety of such sieves, with the two most common such sieves being combinatorial sieves (such as the beta sieve), based on various combinatorial truncations of the inclusion-exclusion formula, and the Selberg upper bound sieve, based on upper bounds that are the square of a divisor sum. (There is also the large sieve, which is somewhat different in nature and based on almost orthogonality considerations, rather than on any actual sieving, to obtain upper bounds.) We will primarily work with a specific sieve in this notes, namely the beta sieve, and we will not attempt to optimise all the parameters of this sieve (which ultimately means that the almost primality parameter in our results will be somewhat large). For a more detailed study of sieve theory, see the classic text of Halberstam and Richert, or the more recent texts of Iwaniec-Kowalski or of Friedlander-Iwaniec.

Very roughly speaking, the end result of sieve theory is that excepting some degenerate and “exponentially thin” settings (such as those associated with the Mersenne primes), all the orbits which are expected to have a large number of primes, can be proven to at least have a large number of -almost primes for some finite . (Unfortunately, there is a major obstruction, known as the parity problem, which prevents sieve theory from lowering all the way to ; see this blog post for more discussion.) One formulation of this principle was established by Bourgain, Gamburd, and Sarnak:

Theorem 1 (Bourgain-Gamburd-Sarnak) Let be a subgroup of which is not virtually solvable. Let be a polynomial with integer coefficients obeying the following primitivity condition: for any positive integer , there exists such that is coprime to . Then there exists an such that there are infinitely many with non-zero and -almost prime.

This is not the strongest version of the Bourgain-Gamburd-Sarnak theorem, but it captures the general flavour of their results. Note that the theorem immediately implies an analogous result for orbits , in which is now a polynomial from to , and one uses instead of . It is in fact conjectured that one can set here, but this is well beyond current technology. For the purpose of reaching , it is very natural to impose the primitivity condition, but as long as one is content with larger values of , it is possible to relax the primitivity condition somewhat; see the paper of Bourgain, Gamburd, and Sarnak for more discussion.

By specialising to the polynomial , we conclude as a corollary that as long as is primitive in the sense that it contains matrices with all coefficients coprime to for any given , then contains infinitely many matrices whose elements are all -almost primes for some depending only on . For further applications of these sorts of results, for instance to Appolonian packings, see the paper of Bourgain, Gamburd, and Sarnak.

It turns out that to prove Theorem 1, the Cayley expansion results in from the previous set of notes are not quite enough; one needs a more general Cayley expansion result in where is square-free but not necessarily prime. The proof of this expansion result uses the same basic methods as in the case, but is significantly more complicated technically, and we will only discuss it briefly here. As such, we do not give a complete proof of Theorem 1, but hopefully the portion of the argument presented here is still sufficient to give an impression of the ideas involved.

254B, Notes 2: Cayley graphs and Kazhdan’s property (T)

In the previous set of notes we introduced the notion of expansion in arbitrary -regular graphs. For the rest of the course, we will now focus attention primarily to a special type of -regular graph, namely a Cayley graph.

Definition 1 (Cayley graph) Let be a group, and let be a finite subset of . We assume that is symmetric (thus whenever ) and does not contain the identity (this is to avoid loops). Then the (right-invariant) Cayley graph is defined to be the graph with vertex set and edge set , thus each vertex is connected to the elements for , and so is a -regular graph.

Example 2 The graph in Exercise 3 of Notes 1 is the Cayley graph on with generators .

Remark 3 We call the above Cayley graphs right-invariant because every right translation on is a graph automorphism of . This group of automorphisms acts transitively on the vertex set of the Cayley graph. One can thus view a Cayley graph as a homogeneous space of , as it “looks the same” from every vertex. One could of course also consider left-invariant Cayley graphs, in which is connected to rather than . However, the two such graphs are isomorphic using the inverse map , so we may without loss of generality restrict our attention throughout to left Cayley graphs.

Remark 4 For minor technical reasons, it will be convenient later on to allow to contain the identity and to come with multiplicity (i.e. it will be a multiset rather than a set). If one does so, of course, the resulting Cayley graph will now contain some loops and multiple edges.
For the purposes of building expander families, we would of course want the underlying group to be finite. However, it will be convenient at various times to “lift” a finite Cayley graph up to an infinite one, and so we permit to be infinite in our definition of a Cayley graph.

We will also sometimes consider a generalisation of a Cayley graph, known as a Schreier graph:

Definition 5 (Schreier graph) Let be a finite group that acts (on the left) on a space , thus there is a map from to such that and for all and . Let be a symmetric subset of which acts freely on in the sense that for all and , and for all distinct and . Then the Schreier graph is defined to be the graph with vertex set and edge set .

Example 6 Every Cayley graph is also a Schreier graph , using the obvious left-action of on itself. The -regular graphs formed from permutations that were studied in the previous set of notes is also a Schreier graph provided that for all distinct , with the underlying group being the permutation group (which acts on the vertex set in the obvious manner), and .

Exercise 7 If is an even integer, show that every -regular graph is a Schreier graph involving a set of generators of cardinality . (Hint: you may assume without proof Petersen’s 2-factor theorem, which asserts that every -regular graph with even can be decomposed into edge-disjoint -regular graphs. Now use the previous example.)

We return now to Cayley graphs. It is easy to characterise qualitative expansion properties of Cayley graphs:

Exercise 8 (Qualitative expansion) Let be a finite Cayley graph.

• (i) Show that is a one-sided -expander for for some if and only if generates .
• (ii) Show that is a two-sided -expander for for some if and only if generates , and furthermore intersects each index subgroup of .

We will however be interested in more quantitative expansion properties, in which the expansion constant is independent of the size of the Cayley graph, so that one can construct non-trivial expander families of Cayley graphs.
One can analyse the expansion of Cayley graphs in a number of ways. For instance, by taking the edge expansion viewpoint, one can study Cayley graphs combinatorially, using the product set operation

of subsets of .

Exercise 9 (Combinatorial description of expansion) Let be a family of finite -regular Cayley graphs. Show that is a one-sided expander family if and only if there is a constant independent of such that for all sufficiently large and all subsets of with .

One can also give a combinatorial description of two-sided expansion, but it is more complicated and we will not use it here.

Exercise 10 (Abelian groups do not expand) Let be a family of finite -regular Cayley graphs, with the all abelian, and the generating . Show that are a one-sided expander family if and only if the Cayley graphs have bounded cardinality (i.e. ). (Hint: assume for contradiction that is a one-sided expander family with , and show by two different arguments that grows at least exponentially in and also at most polynomially in , giving the desired contradiction.)

The left-invariant nature of Cayley graphs also suggests that such graphs can be profitably analysed using some sort of Fourier analysis; as the underlying symmetry group is not necessarily abelian, one should use the Fourier analysis of non-abelian groups, which is better known as (unitary) representation theory. The Fourier-analytic nature of Cayley graphs can be highlighted by recalling the operation of convolution of two functions , defined by the formula

This convolution operation is bilinear and associative (at least when one imposes a suitable decay condition on the functions, such as compact support), but is not commutative unless is abelian. (If one is more algebraically minded, one can also identify (when is finite, at least) with the group algebra , in which case convolution is simply the multiplication operation in this algebra.) The adjacency operator on a Cayley graph can then be viewed as a convolution

where is the probability density

where is the Kronecker delta function on . Using the spectral definition of expansion, we thus see that is a one-sided expander if and only if

whenever is orthogonal to the constant function , and is a two-sided expander if

whenever is orthogonal to the constant function .
We remark that the above spectral definition of expansion can be easily extended to symmetric sets which contain the identity or have multiplicity (i.e. are multisets). (We retain symmetry, though, in order to keep the operation of convolution by self-adjoint.) In particular, one can say (with some slight abuse of notation) that a set of elements of (possibly with repetition, and possibly with some elements equalling the identity) generates a one-sided or two-sided -expander if the associated symmetric probability density

obeys either (2) or (3).
We saw in the last set of notes that expansion can be characterised in terms of random walks. One can of course specialise this characterisation to the Cayley graph case:

Exercise 11 (Random walk description of expansion) Let be a family of finite -regular Cayley graphs, and let be the associated probability density functions. Let be a constant.

• Show that the are a two-sided expander family if and only if there exists a such that for all sufficiently large , one has for some , where denotes the convolution of copies of .
• Show that the are a one-sided expander family if and only if there exists a such that for all sufficiently large , one has for some .

In this set of notes, we will connect expansion of Cayley graphs to an important property of certain infinite groups, known as Kazhdan’s property (T) (or property (T) for short). In 1973, Margulis exploited this property to create the first known explicit and deterministic examples of expanding Cayley graphs. As it turns out, property (T) is somewhat overpowered for this purpose; in particular, we now know that there are many families of Cayley graphs for which the associated infinite group does not obey property (T) (or weaker variants of this property, such as property ). In later notes we will therefore turn to other methods of creating Cayley graphs that do not rely on property (T). Nevertheless, property (T) is of substantial intrinsic interest, and also has many connections to other parts of mathematics than the theory of expander graphs, so it is worth spending some time to discuss it here.
The material here is based in part on this recent text on property (T) by Bekka, de la Harpe, and Valette (available online here).

Cayley graphs and the geometry of groups

In most undergraduate courses, groups are first introduced as a primarily algebraic concept – a set equipped with a number of algebraic operations (group multiplication, multiplicative inverse, and multiplicative identity) and obeying a number of rules of algebra (most notably the associative law). It is only somewhat later that one learns that groups are not solely an algebraic object, but can also be equipped with the structure of a manifold (giving rise to Lie groups) or a topological space (giving rise to topological groups). (See also this post for a number of other ways to think about groups.)

Another important way to enrich the structure of a group is to give it some geometry. A fundamental way to provide such a geometric structure is to specify a list of generators of the group . Let us call such a pair a generated group; in many important cases the set of generators is finite, leading to a finitely generated group. A generated group gives rise to the word metric on , defined to be the maximal metric for which for all and (or more explicitly, is the least for which for some and ). This metric then generates the balls . In the finitely generated case, the are finite sets, and the rate at which the cardinality of these sets grow in is an important topic in the field of geometric group theory. The idea of studying a finitely generated group via the geometry of its metric goes back at least to the work of Dehn.

One way to visualise the geometry of a generated group is to look at the (labeled) Cayley colour graph of the generated group . This is a directed coloured graph, with edges coloured by the elements of , and vertices labeled by elements of , with a directed edge of colour from to for each and . The word metric then corresponds to the graph metric of the Cayley graph.

For instance, the Cayley graph of the cyclic group with a single generator (which we draw in green) is given as

while the Cayley graph of the same group but with the generators (which we draw in blue and red respectively) is given as

We can thus see that the same group can have somewhat different geometry if one changes the set of generators. For instance, in a large cyclic group , with a single generator the Cayley graph “looks one-dimensional”, and balls grow linearly in until they saturate the entire group, whereas with two generators chosen at random, the Cayley graph “looks two-dimensional”, and the balls typically grow quadratically until they saturate the entire group.

Cayley graphs have three distinguishing properties:

• (Regularity) For each colour , every vertex has a single -edge leading out of , and a single -edge leading into .
• (Connectedness) The graph is connected.
• (Homogeneity) For every pair of vertices , there is a unique coloured graph isomorphism that maps to .

It is easy to verify that a directed coloured graph is a Cayley graph (up to relabeling) if and only if it obeys the above three properties. Indeed, given a graph with the above properties, one sets to equal the (coloured) automorphism group of the graph ; arbitrarily designating one of the vertices of to be the identity element , we can then identify all the other vertices in with a group element. One then identifies each colour with the vertex that one reaches from by an -coloured edge. Conversely, every Cayley graph of a generated group is clearly regular, is connected because generates , and has isomorphisms given by right multiplication for all . (The regularity and connectedness properties already ensure the uniqueness component of the homogeneity property.)

From the above equivalence, we see that we do not really need the vertex labels on the Cayley graph in order to describe a generated group, and so we will now drop these labels and work solely with unlabeled Cayley graphs, in which the vertex set is not already identified with the group. As we saw above, one just needs to designate a marked vertex of the graph as the “identity” or “origin” in order to turn an unlabeled Cayley graph into a labeled Cayley graph; but from homogeneity we see that all vertices of an unlabeled Cayley graph “look the same” and there is no canonical preference for choosing one vertex as the identity over another. I prefer here to keep the graphs unlabeled to emphasise the homogeneous nature of the graph.

It is instructive to revisit the basic concepts of group theory using the language of (unlabeled) Cayley graphs, and to see how geometric many of these concepts are. In order to facilitate the drawing of pictures, I work here only with small finite groups (or Cayley graphs), but the discussion certainly is applicable to large or infinite groups (or Cayley graphs) also.

For instance, in this setting, the concept of abelianness is analogous to that of a flat (zero-curvature) geometry: given any two colours , a directed path with colours (adopting the obvious convention that the reversal of an -coloured directed edge is considered an -coloured directed edge) returns to where it started. (Note that a generated group is abelian if and only if the generators in pairwise commute with each other.) Thus, for instance, the two depictions of above are abelian, whereas the group , which is also the dihedral group of the triangle and thus admits the Cayley graph

is not abelian.

A subgroup of a generated group can be easily described in Cayley graph language if the generators of happen to be a subset of the generators of . In that case, if one begins with the Cayley graph of and erases all colours except for those colours in , then the graph foliates into connected components, each of which is isomorphic to the Cayley graph of . For instance, in the above Cayley graph depiction of , erasing the blue colour leads to three copies of the red Cayley graph (which has as its structure group), while erasing the red colour leads to two copies of the blue Cayley graph (which as as its structure group). If is not contained in , then one has to first “change basis” and add or remove some coloured edges to the original Cayley graph before one can obtain this formulation (thus for instance contains two more subgroups of order two that are not immediately apparent with this choice of generators). Nevertheless the geometric intuition that subgroups are analogous to foliations is still quite a good one.

We saw that a subgroup of a generated group with foliates the larger Cayley graph into -connected components, each of which is a copy of the smaller Cayley graph. The remaining colours in then join those -components to each other. In some cases, each colour will connect a -component to exactly one other -component; this is the case for instance when one splits into two blue components. In other cases, a colour can connect a -component to multiple -components; this is the case for instance when one splits into three red components. The former case occurs precisely when the subgroup is normal. (Note that a subgroup of a generated group is normal if and only if left-multiplication by a generator of maps right-cosets of to right-cosets of .) We can then quotient out the Cayley graph from , leading to a quotient Cayley graph whose vertices are the -connected components of , and the edges are projected from in the obvious manner. We can then view the original graph as a bundle of -graphs over a base -graph (or equivalently, an extension of the base graph by the fibre graph ); for instance can be viewed as a bundle of the blue graph over the red graph , but not conversely. We thus see that the geometric analogue of the concept of a normal subgroup is that of a bundle. The generators in can be viewed as describing a connection on that bundle.

Note, though, that the structure group of this connection is not simply , unless is a central subgroup; instead, it is the larger group , the semi-direct product of with its automorphism group. This is because a non-central subgroup can be “twisted around” by operations such as conjugation by a generator . So central subgroups are analogous to the geometric notion of a principal bundle. For instance, here is the Heisenberg group

over the field of two elements, which one can view as a central extension of (the blue and green edges, after quotienting) by (the red edges):

Note how close this group is to being abelian; more generally, one can think of nilpotent groups as being a slight perturbation of abelian groups.

In the case of (viewed as a bundle of the blue graph over the red graph ), the base graph is in fact embedded (three times) into the large graph . More generally, the base graph can be lifted back into the extension if and only if the short exact sequence splits, in which case becomes a semidirect product of and a lifted copy of . Not all bundles can be split in this fashion. For instance, consider the group , with the blue generator and the red generator :

This is a -bundle over that does not split; the blue Cayley graph of is not visible in the graph directly, but only after one quotients out the red fibre subgraph. The notion of a splitting in group theory is analogous to the geometric notion of a global gauge. The existence of such a splitting or gauge, and the relationship between two such splittings or gauges, are controlled by the group cohomology of the sequence .

Even when one has a splitting, the bundle need not be completely trivial, because the bundle is not principal, and the connection can still twist the fibres around. For instance, when viewed as a bundle over with fibres splits, but observe that if one uses the red generator of this splitting to move from one copy of the blue graph to the other, that the orientation of the graph changes. The bundle is trivialisable if and only if is a direct summand of , i.e. splits as a direct product of a lifted copy of . Thus we see that the geometric analogue of a direct summand is that of a trivialisable bundle (and that trivial bundles are then the analogue of direct products). Note that there can be more than one way to trivialise a bundle. For instance, with the Klein four-group ,

the red fibre is a direct summand, but one can use either the blue lift of or the green lift of as the complementary factor.

Approximate subgroups of linear groups

Emmanuel Breuillard, Ben Green, and I have just uploaded to the arXiv our paper “Approximate subgroups of linear groups“, submitted to GAFA. This paper contains (the first part) of the results announced previously by us; the second part of these results, concerning expander groups, will appear subsequently. The release of this paper has been coordinated with the release of a parallel paper by Pyber and Szabo (previously announced within an hour(!) of our own announcement).

Our main result describes (with polynomial accuracy) the “sufficiently Zariski dense” approximate subgroups of simple algebraic groups , or more precisely absolutely almost simple algebraic groups over , such as . More precisely, define a -approximate subgroup of a genuine group to be a finite symmetric neighbourhood of the identity (thus and ) such that the product set can be covered by left-translates (and equivalently, right-translates) of .

Let be a field, and let be its algebraic closure. For us, an absolutely almost simple algebraic group over is a linear algebraic group defined over (i.e. an algebraic subvariety of for some with group operations given by regular maps) which is connected (i.e. irreducible), and such that the completion has no proper normal subgroups of positive dimension (i.e. the only normal subgroups are either finite, or are all of . To avoid degeneracies we also require to be non-abelian (i.e. not one-dimensional). These groups can be classified in terms of their associated finite-dimensional simple complex Lie algebra, which of course is determined by its Dynkin diagram, together with a choice of weight lattice (and there are only finitely many such choices once the Lie algebra is fixed). However, the exact classification of these groups is not directly used in our work.

Our first main theorem classifies the approximate subgroups of such a group in the model case when generates the entire group , and is finite; they are either very small or very large.

Theorem 1 (Approximate groups that generate) Let be an absolutely almost simple algebraic group over . If is finite and is a -approximate subgroup of that generates , then either or , where the implied constants depend only on .

The hypothesis that generates cannot be removed completely, since if was a proper subgroup of of size intermediate between that of the trivial group and of , then the conclusion would fail (with ). However, one can relax the hypothesis of generation to that of being sufficiently Zariski-dense in . More precisely, we have

Theorem 2 (Zariski-dense approximate groups) Let be an absolutely almost simple algebraic group over . If is a -approximate group) is not contained in any proper algebraic subgroup of of complexity at most (where is sufficiently large depending on ), then either or , where the implied constants depend only on and is the group generated by .

Here, we say that an algebraic variety has complexity at most if it can be cut out of an ambient affine or projective space of dimension at most by using at most polynomials, each of degree at most . (Note that this is not an intrinsic notion of complexity, but will depend on how one embeds the algebraic variety into an ambient space; but we are assuming that our algebraic group is a linear group and thus comes with such an embedding.)

In the case when , the second option of this theorem cannot occur since is infinite, leading to a satisfactory classification of the Zariski-dense approximate subgroups of almost simple connected algebraic groups over . On the other hand, every approximate subgroup of is Zariski-dense in some algebraic subgroup, which can be then split as an extension of a semisimple algebraic quotient group by a solvable algebraic group (the radical of the Zariski closure). Pursuing this idea (and glossing over some annoying technical issues relating to connectedness), together with the Freiman theory for solvable groups over due to Breuillard and Green, we obtain our third theorem:

Theorem 3 (Freiman’s theorem in ) Let be a -approximate subgroup of . Then there exists a nilpotent -approximate subgroup of size at most , such that is covered by translates of .

This can be compared with Gromov’s celebrated theorem that any finitely generated group of polynomial growth is virtually nilpotent. Indeed, the above theorem easily implies Gromov’s theorem in the case of finitely generated subgroups of .

By fairly standard arguments, the above classification theorems for approximate groups can be used to give bounds on the expansion and diameter of Cayley graphs, for instance one can establish a conjecture of Babai and Seress that connected Cayley graphs on absolutely almost simple groups over a finite field have polylogarithmic diameter at most. Applications to expanders include the result on Suzuki groups mentioned in a previous post; further applications will appear in a forthcoming paper.

Apart from the general structural theory of algebraic groups, and some quantitative analogues of the basic theory of algebraic geometry (which we chose to obtain via ultrafilters, as discussed in this post), we rely on two basic tools. Firstly, we use a version of the pivot argument developed first by Konyagin and Bourgain-Glibichuk-Konyagin in the setting of sum-product estimates, and generalised to more non-commutative settings by Helfgott; this is discussed in this previous post. Secondly, we adapt an argument of Larsen and Pink (which we learned from a paper of Hrushovski) to obtain a sharp bound on the extent to which a sufficiently Zariski-dense approximate groups can concentrate in a (bounded complexity) subvariety; this is discussed at the end of this blog post.

Kleiner’s proof of Gromov’s theorem

This week there is a conference here at IPAM on expanders in pure and applied mathematics. I was an invited speaker, but I don’t actually work in expanders per se (though I am certainly interested in them). So I spoke instead about the recent simplified proof by Kleiner of the celebrated theorem of Gromov on groups of polynomial growth. (This proof does not directly mention expanders, but the argument nevertheless hinges on the absence of expansion in the Cayley graph of a group of polynomial growth, which is exhibited through the smoothness properties of harmonic functions on such graphs.)