[This post is authored by Ben Green, who has kindly “guest blogged” this week’s “open problem of the week”. – T.]
In an earlier blog post Terry discussed Freiman’s theorem. The name of Freiman is attached to a growing body of theorems which take some rather “combinatorial” hypothesis, such that the sumset |A+A| of some set A is small, and deduce from it rather “algebraic” information (such that A is contained in a subspace or a grid).
The easiest place to talk about Freiman’s theorem is in the finite field model (see my survey article on this subject for a full discussion). Here it was shown by Ruzsa that if |A+A| is at most
then A is contained in a subspace of size no more than about
. The exponent has been improved a few times since Ruzsa’s paper, the best result currently in print being due to Sanders, who obtains an upper bound of
. Terry and I are in the process of writing a paper which obtains
, which is best possible in view of the example
where
; this set has doubling roughly K but is not contained in a subspace of dimension smaller than 2K.
This result has an air of finality (except for the true nature of the o(K) term, which represents an interesting open problem). This is something of an illusion, however. Even using this theorem, one loses an exponential every time one tries to transition between “combinatorial” structure and “algebraic” structure and back again. Indeed if one knows that A is contained in a subspace of size then the strongest assertion one can make about the doubling of A is that it is at most
.
The Polynomial Freiman-Ruzsa conjecture (PFR), in , hypothesises a more precise structure theorem for sets with small doubling. Using this
conjecture, one may flit back and forth between combinatorial and algebraic structure with only polynomial losses. Ruzsa attributes the conjecture to
Marton: it states that if A has doubling at most K then A is contained in the union of translates of some subspace H of size at most |A|.
Various equivalent formulations of this may be found in my survey article referenced above. They are all due to Imre Ruzsa and here is one I find particularly tantalising: suppose that is a function such that the size of the set
is at most K. Then f can be written as g + h, where g is linear and the cardinality
of the image of h is bounded by a polynomial in K. It is fairly clear that h can be made at most
; simply define f on the basis vectors and extend linearly. Now I come to think of it, for this variant of the problem I’m not sure a bound much better than
is known at all.
The main open problem in the area is to prove the PFR. There are two other groups of problems which might be highlighted here:
- Generalising the PFR to other groups. Even for the group
, there is some controversy about the statement of PFR. I’d be happy enough to
formulate the following conjecture: If the doubling of A is at most K then there is a convex body P of dimensionand volume at most |A|
together with an affine mapsuch that A lies in the union of at most
translates of A.It may be that some slightly technical “roundness” condition on P is desirable for applications. It is not clear at present whether P can be
taken to be a box; this seems to involve some rather tricky geometry of numbers issues though one suspects the answer may be “no”. - Applications. The PFR seems to be the key to unlocking the relationship between combinatorial and algebraic structure. But what applications does
it have? It could be very helpful in the theory of sum-product estimates; I know for example that it easily implies a (very difficult) result of
Bourgain and Chang which states that, where f(k) tends to infinity with k. Could it be helpful with, say, Waring’s problem? If the
powers A are not a basis of small order then the iterated sumset
must be closer than one expects to
, for some i. One might then hope to show that the
powers have some kind of weak algebraic structure, a possibility which could be eliminated by other (number-theoretical means). I don’t have any idea how to do either part of this at the moment.
- Another possible application might be to the following very nice question: If A is a set of square numbers, is
for some positive c? Again, one could use PFR to show that if this is not the case then there is a set of squares with high density on a “grid” (image of a convex body). One might then hope to adapt techniques of Bombieri, Zannier, Granville and Pintz which showed that squares cannot concentrate overly much on a progression. I particularly like this question because it seems very closely related to a lovely question of Rudin: Are the squares
a
set for some p less than 4? I refer the reader to Bourgain’s survey article on
sets for more information.

18 comments
Comments feed for this article
12 March, 2007 at 12:06 pm
Gil
Marton’s conjecture and the many equivalent formulation by Ruzsa are very beautiful. Let me mention something little that I find interesting: You have these two equivalent formulations (1) and (2) (from Green’s paper). (1) says that we can find inside A a subset A’ of size at least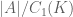 which is contained in a coset of size at most
which is contained in a coset of size at most  . (2) says that you can cover |A| with
. (2) says that you can cover |A| with  such sets A’. The non trivial implication (1) –> (2) is rather easy in view of Ruzsa’s lemma 1.2 (in Green’s paper).
such sets A’. The non trivial implication (1) –> (2) is rather easy in view of Ruzsa’s lemma 1.2 (in Green’s paper).
In abstract combinatorial settings you can expect (if things go your way and you can maintain the assumptions after deleting A’) an additional factor of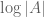 moving from (1) to (2). Some sort of integrality gap. And getting rid of it is at times impossible, at times open, and at times hard. Here, somehow the additive structure makes (1) and (2) quite easily, almost the same. (In combinatorial geometry you also sometimes see similar phenomena.)
moving from (1) to (2). Some sort of integrality gap. And getting rid of it is at times impossible, at times open, and at times hard. Here, somehow the additive structure makes (1) and (2) quite easily, almost the same. (In combinatorial geometry you also sometimes see similar phenomena.)
12 March, 2007 at 12:53 pm
Terence Tao
Dear Gil,
I tend to view the Freiman-Ruzsa theory as more of an “approximate group theory” than a purely combinatorial theory, to emphasise the additional algebraic (rather than combinatorial) structure present.
For instance, if H and L are two finite subgroups of an abelian group G, and K is an integer, then it is not hard to show that the following two statements are equivalent: (1) H has a subset of size at least which is contained in a coset of L, and (2) H is covered by K translates of L. Indeed, the equivalence is essentially the first homomorphism theorem from undergraduate algebra. Ruzsa’s lemma is thus the robust version of this theorem.
which is contained in a coset of L, and (2) H is covered by K translates of L. Indeed, the equivalence is essentially the first homomorphism theorem from undergraduate algebra. Ruzsa’s lemma is thus the robust version of this theorem.
I am hoping that eventually we will be able to “robustify” many other results in group theory (or ring theory, etc.) to extend to approximate groups. For instance, as I mentioned in an earlier post, Freiman’s theorem can be viewed as a robust version of the classification of finite abelian groups as the direct product of cyclic groups (or perhaps, a classification of the finitely generated abelian groups as the direct product of cyclic groups and copies of Z). Ultimately we might hope to manipulate “1%-structured objects” (such as sets which are closed under addition 1% of the time) with the almost the same degree of versatility as we currently enjoy while manipulating “100%-structured objects” (such as sets which are closed under addition 100% of the time, i.e. groups). An intermediate stage in this program would be to study “99%-structured objects”, e.g. a finite group with 1% of its elements removed and another 1% of garbage elements added. Here we seem to have a very good theory, due to the use of majority-vote and similar tools to “clean up” all the noise.
12 March, 2007 at 3:46 pm
Greg Kuperberg
On the general subject of robust versions of results in group theory, there is the theorem of Ben-Or, Coppersmith, Luby, and Rubinfeld that an approximate homomorphism between two finite groups is close to a group homomorphism.
13 March, 2007 at 8:08 am
ben green
Greg,
Yes, indeed there is. They definitely beat us additive combinatorialists to this whole game of making exact algebraic structures out of approximate ones. But I recently discovered that essentially the same idea occurs in a paper of Fournier from 1977 called “Sharpness of Young’s inequality for convolution“.
He is interested in the following question: for which groups G is the Young inequality, which states (say) that , basically sharp? I.e. in which circumstances can you improve it to the statement that
, basically sharp? I.e. in which circumstances can you improve it to the statement that 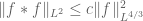 , where c is less than one?
, where c is less than one?
He shows that one can do this provided that G does not have compact open subgroups (note that G does not need to be abelian).
You can sort of see the connection to what we’re talking about here – if there is some f for which is about as big as
is about as big as  then this means (after expanding out) that the support of f has got to be 99 percent closed under addition. He then goes on to show that the support must be close to a true subgroup.
then this means (after expanding out) that the support of f has got to be 99 percent closed under addition. He then goes on to show that the support must be close to a true subgroup.
So I sort of think of Fournier as the father of approximate, or “99 percent” theory, unless someone can point me to an earlier paper :-)
22 March, 2007 at 6:32 pm
Freiman's theorem in finite fields via extremal set theory « What’s new
[…] theorem in the 2-torsion case, and in particular getting some partial results on the polynomial Freiman-Ruzsa conjecture. Specifically, we show that if has doubling constant at most K, thus , then A can be contained in […]
9 November, 2008 at 2:56 pm
A counterexample to a strong polynomial Freiman-Ruzsa conjecture « What’s new
[…] open problems in additive combinatorics is the polynomial Freiman-Ruzsa conjecture, which Ben Green guest blogged about here some time ago. It has many equivalent formulations, but here is one involving […]
6 December, 2009 at 6:54 pm
Non-commutative Freiman theorems, and model theory « What’s new
[…] description of sets of small doubling. (For more on the question of improving the constants, see this guest blog post of Ben […]
13 January, 2012 at 7:49 pm
254B, Notes 4: The Bourgain-Gamburd expansion machine « What’s new
[…] which are qualitatively similar in spirit, but have much worse quantitative bounds (though there is some hope in the case of Freiman’s theorem to only lose polynomial bounds with some improvement of […]
19 March, 2014 at 5:30 pm
Metric entropy analogues of sum set theory | What's new
[…] does, however the known bounds in the latter theorem are worse than polynomial in (although it is conjectured otherwise), whereas the elementary estimates are almost all polynomial in […]
19 November, 2019 at 12:41 pm
Khot,Minzer,Safra on approximate sections of sheaves | Quomodocumque
[…] is meant to recall the principle from additive number theory that an approximate subgroup is approximately a subgroup, as in e.g. […]
27 June, 2023 at 12:45 pm
Sumsets and entropy revisited | What's new
[…] preprint “Sumsets and entropy revisited“. This paper uses entropy methods to attack the Polynomial Freiman-Ruzsa (PFR) conjecture, which we study in the following two […]
27 June, 2023 at 2:49 pm
Sumsets and entropy revisited | What's new - Being Teaching 2023
[…] “Sumsets and entropy revisited“. This paper makes use of entropy strategies to assault the Polynomial Freiman-Ruzsa (PFR) conjecture, which we examine within the following two […]
27 June, 2023 at 3:28 pm
Sumsets and entropy revisited | What's new - Gud Learn
[…] and entropy revisited“. This paper makes use of entropy techniques to assault the Polynomial Freiman-Ruzsa (PFR) conjecture, which we research in the adhering to 2 […]
8 August, 2023 at 4:00 pm
Sumsets and entropy revisited | What's new - keiseronlineuniversity.com
[…] “Sumsets and entropy revisited“. This paper makes use of entropy strategies to assault the Polynomial Freiman-Ruzsa (PFR) conjecture, which we examine within the following two […]
13 November, 2023 at 3:04 am
Marton’s “Polynomial Freiman-Rusza” Conjecture was Settled by the A-Team. | Combinatorics and more
[…] conjecture” was certainly a holy grail of additive combinatorics. (Here is a 2007 short blog post by Ben Green presenting the problem.) Tim Gowers, Ben Green, Freddie Manners and Terry Tao have now solved it […]
13 November, 2023 at 9:41 am
On a conjecture of Marton | What's new
[…] paper “On a conjecture of Marton“. This paper establishes a version of the notorious Polynomial Freiman–Ruzsa conjecture (first proposed by Katalin […]
13 November, 2023 at 10:54 am
On a conjecture of Marton - Gud Learn
[…] paper “On a conjecture of Marton“. This paper develops a variation of the well-known Polynomial Freiman–Ruzsa conjecture (very first proposed by Katalin […]
4 April, 2024 at 2:06 pm
Marton’s conjecture in abelian groups with bounded torsion | What's new
[…] This paper fully resolves a conjecture of Katalin Marton (the bounded torsion case of the Polynomial Freiman–Ruzsa conjecture (first proposed by Katalin […]