Ben Green, Freddie Manners and I have just uploaded to the arXiv our preprint “Sumsets and entropy revisited“. This paper uses entropy methods to attack the Polynomial Freiman-Ruzsa (PFR) conjecture, which we study in the following two forms:
Conjecture 1 (Weak PFR over) Let
be a finite non-empty set whose doubling constant
is at most
. Then there is a subset
of
of density
that has affine dimension
(i.e., it is contained in an affine space of dimension
).
Conjecture 2 (PFR over) Let
be a non-empty set whose doubling constant
is at most
. Then
can be covered by
cosets of a subspace of cardinality at most
.
Our main results are then as follows.
Theorem 3 Ifwith
, then
- (i) There is a subset
of
of density
of “skew-dimension” (or “query complexity”)
.
- (ii) There is a subset
of
of density
of affine dimension
(where
goes to zero as
).
- (iii) If Conjecture 2 holds, then there is a subset
of
of density
of affine dimension
. In other words, Conjecture 2 implies Conjecture 1.
The skew-dimension of a set is a quantity smaller than the affine dimension which is defined recursively; the precise definition is given in the paper, but suffice to say that singleton sets have dimension , and a set
whose projection to
has skew-dimension at most
, and whose fibers in
have skew-dimension at most
for any
, will have skew-dimension at most
. (In fact, the skew-dimension is basically the largest quantity which obeys all of these properties.)
Part (i) of this theorem was implicitly proven by Pálvölgi and Zhelezov by a different method. Part (ii) with replaced by
was established by Manners. To our knowledge, part (iii) is completely new.
Our proof strategy is to establish these combinatorial additive combinatorics results by using entropic additive combinatorics, in which we replace sets with random variables
, and cardinality with (the exponential of) Shannon entropy. This is in order to take advantage of some superior features of entropic additive combinatorics, most notably good behavior with respect to homomorphisms.
For instance, the analogue of the combinatorial doubling constant of a finite non-empty subset
of an abelian group
, is the entropy doubling constant
Our first main result is a “99% inverse theorem” for entropic Ruzsa distance: if is sufficiently small, then there exists a finite subgroup
of
such that
to a set
of small doubling, which can then be related to a subgroup
by standard inverse theorems; this gives a weak version of (1) (roughly speaking losing a square root in the bound), and some additional analysis is needed to bootstrap this initial estimate back to (1).
We now sketch how these tools are used to prove our main theorem. For (i), we reduce matters to establishing the following bilinear entropic analogue: given two non-empty finite subsets of
, one can find subsets
,
with
For parts (ii) and (iii), we first use an entropic version of an observation of Manners that sets of small doubling in must be irregularly distributed modulo
. A clean formulation of this in entropic language is the inequality
As one byproduct of our analysis we also obtain an appealing entropic reformulation of Conjecture 2, namely that if is an
-valued random variable then there exists a subspace
of
such that

13 comments
Comments feed for this article
28 June, 2023 at 11:19 am
Anonymous
Is there a conjectured value for the best exponent in theorem 3(ii) (instead of 5/3)?
29 June, 2023 at 2:06 pm
Terence Tao
The conjectured exponent is 1 (this is Conjecture 1).
29 June, 2023 at 8:47 am
Joe
In Theorem 3 (iii),’There’ should be typed in lowercase.
[Corrected, thanks – T.]
2 July, 2023 at 9:54 am
Gil Kalai
I find it surprising and remarkable that a result over Z can be derived from a similar result over Z/2Z. Terry, can you elaborate more on how it works?
2 July, 2023 at 12:49 pm
Terence Tao
For simplicity I will describe the argument in combinatorial language rather than entropic language, although the combinatorial argument doesn’t quite work as stated and one has to move to the entropy formulation to make everything go through. (Also to make the inductive argument close properly one has to work with a “bilinear” formulation in which one has two sets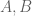 to induct on rather than a single set
to induct on rather than a single set  , but I will ignore this complication.)
, but I will ignore this complication.)
The first key observation is a remarkable observation of Manners that says, roughly speaking, that if a subset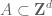 has small doubling, then
has small doubling, then  is also close (in Ruzsa distance) to the dilate
is also close (in Ruzsa distance) to the dilate 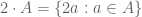 (which already strongly hints at the low dimensionality of a large portion of
(which already strongly hints at the low dimensionality of a large portion of  , but does not yet establish it). This comes from the inequality
, but does not yet establish it). This comes from the inequality  which is proven by a double counting argument similar to the one used to prove the Ruzsa triangle inequality
which is proven by a double counting argument similar to the one used to prove the Ruzsa triangle inequality  (the point being that because of the identity
(the point being that because of the identity 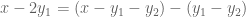 , every element of
, every element of 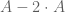 generates
generates  distinct pairs in
distinct pairs in 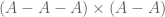 ).
).
If we project the integer lattice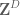 down to the finite field vector space
down to the finite field vector space 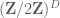 , then the dilate
, then the dilate 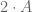 gets sent to 0. As a consequence, we see that the projection of
gets sent to 0. As a consequence, we see that the projection of  to
to 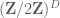 has to be quite small; also, since
has to be quite small; also, since  has small doubling, the projection has small doubling also. From this and the known progress on PFR, one can relate the projection of
has small doubling, the projection has small doubling also. From this and the known progress on PFR, one can relate the projection of  efficiently to a low dimensional subspace of
efficiently to a low dimensional subspace of 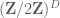 , whose inverse images are sublattices of
, whose inverse images are sublattices of 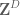 . If
. If  is much larger than the dimension of this subspace, one can (in the entropic setting) use this to locate a coset of this sublattice inside of which
is much larger than the dimension of this subspace, one can (in the entropic setting) use this to locate a coset of this sublattice inside of which  is still quite large, and has better doubling properties than the original set
is still quite large, and has better doubling properties than the original set  . An induction on the dimension
. An induction on the dimension  then lets one close the argument.
then lets one close the argument.
27 July, 2023 at 12:53 pm
CSperson
Why do you use the phrase “query complexity”?
29 July, 2023 at 11:09 am
Terence Tao
The terminology was first introduced to this context by Zhelezov and Pálvölgyi (see page 3 for the explanation).
31 July, 2023 at 6:19 am
CSperson
May be should be called ‘generalized decision tree complexity’ or something along those lines. Someone might know better on the analogy here.
10 October, 2023 at 9:52 am
Anonymous
It would be interesting to have an analog for Theorem 3 (i) for $F_2^n$. Possibly it may have some connections to the log rank conjecture in computer science?
10 October, 2023 at 2:14 pm
Terence Tao
We were actually able to get some sort of analogue in finite fields using these entropic methods, but it was really weird and we didn’t find a good use for it (or a clean statement). Roughly speaking, it is similar to 3(i) except that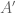 , instead of having query complexity
, instead of having query complexity 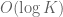 , is instead generated from a point via
, is instead generated from a point via 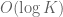 “extension” operations, where an extension from one set
“extension” operations, where an extension from one set 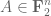 to another
to another 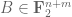 is one of the following three things:
is one of the following three things:
1. Short extension , and
, and  is a subset of
is a subset of 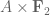 of relative density
of relative density 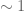 .
.
2. Dense extension. is a subset of
is a subset of 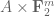 of relative density
of relative density  (say).
(say).
3. Freiman extension. is a graph
is a graph 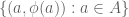 where
where 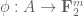 is a “99% Freiman homomorphism”.
is a “99% Freiman homomorphism”.
Of course, we believe the “correct” statement in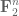 to be the polynomial Freiman-Ruzsa conjecture (Conjecture 2). We have some thoughts on how to improve the current state of the art towards this conjecture, but we don’t see a way to resolve it completely at this point.
to be the polynomial Freiman-Ruzsa conjecture (Conjecture 2). We have some thoughts on how to improve the current state of the art towards this conjecture, but we don’t see a way to resolve it completely at this point.
28 October, 2023 at 8:49 pm
Kaiyi Huang
Hello Terence,
Thanks for your blog post and paper. I am a graduate student recently reading this paper in order to present in a fall school. I find it very accessible and inspiring. However, there are a few questions listed below.
1. In proving the small Ruzsa distance results, the construction of on which the uniform distribution is close to
on which the uniform distribution is close to  induces a Bernoulli random variable
induces a Bernoulli random variable  . Is it a common trick to introduce this
. Is it a common trick to introduce this  ? Can we improve the results in Proposition 1.2 by reducing/removing the
? Can we improve the results in Proposition 1.2 by reducing/removing the 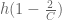 term?
term?
2. The bilinear forms you use in Theorems 7.3 and 9.3 are very different from that of 1.6. How did you come up with the inequality and specifically the functions ?
?
3. Do you have any conjecture on how to further improve Theorem 1.11? Do you think this is the best the entropic method can achieve with a function similar to Theorem 9.3?
Theorem 9.3?
4. What are some future directions? Do we have to come up with some statement different from Theorem 1.11 to attack the conjectures?
4. In the proof of 1.4 in Section 4, I think all the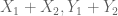 should be replaced by
should be replaced by  , respectively. Of course, this typo does not affect the results.
, respectively. Of course, this typo does not affect the results.
Thanks for reading the questions.
1 November, 2023 at 4:49 pm
Terence Tao
We did not try too strenuously to optimize the arguments, and it is very plausible that by applying entropy inequalities in a slightly different way one could get superior results. Introducing a boolean variable such as to restrict to a “good” event (or to the complementary “exceptional” event) in order to access facts that are available conditioning to that event, is a common trick in this subject.
to restrict to a “good” event (or to the complementary “exceptional” event) in order to access facts that are available conditioning to that event, is a common trick in this subject.
In these sorts of iterative arguments, the bounding functions is usually not known in advance – one first works out what the inductive step gives, which in this case is some assertion of the form “if
is usually not known in advance – one first works out what the inductive step gives, which in this case is some assertion of the form “if 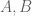 have a certain entropy distance
have a certain entropy distance 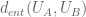 , then I can find some better pair
, then I can find some better pair 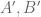 obeying one of several possible improved bounds”, and then one has to hunt for a clean choice of function
obeying one of several possible improved bounds”, and then one has to hunt for a clean choice of function  for which the inductive step will close properly. This often takes some trial and error, especially if the inductive step does not produce a single bound, but rather a disjunction of several possible bounds. Usually one has to explore a few iterations of the inductive step to get a feel of how the bounds might grow in order to propose a guess for
for which the inductive step will close properly. This often takes some trial and error, especially if the inductive step does not produce a single bound, but rather a disjunction of several possible bounds. Usually one has to explore a few iterations of the inductive step to get a feel of how the bounds might grow in order to propose a guess for  , try to close the induction for that
, try to close the induction for that  , and tweak the choice if it didn’t quite work.
, and tweak the choice if it didn’t quite work.
We have a forthcoming paper (with Timothy Gowers) with some significant improvements to the results. Will hopefully be able to report more on this soon. (We will also correct the typos in Section 4 in the next revision of the ms.)
13 November, 2023 at 9:41 am
On a conjecture of Marton | What's new
[…] constant at most is unclear (and perhaps even false). However, it turns out (as discussed in this recent paper of myself with Green and Manners) that things are much better. Here, the analogue of a subset in is a random variable taking […]