This post is a sequel of sorts to my earlier post on hard and soft analysis, and the finite convergence principle. Here, I want to discuss a well-known theorem in infinitary soft analysis – the Lebesgue differentiation theorem – and whether there is any meaningful finitary version of this result. Along the way, it turns out that we will uncover a simple analogue of the Szemerédi regularity lemma, for subsets of the interval rather than for graphs. (Actually, regularity lemmas seem to appear in just about any context in which fine-scaled objects can be approximated by coarse-scaled ones.) The connection between regularity lemmas and results such as the Lebesgue differentiation theorem was recently highlighted by Elek and Szegedy, while the connection between the finite convergence principle and results such as the pointwise ergodic theorem (which is a close cousin of the Lebesgue differentiation theorem) was recently detailed by Avigad, Gerhardy, and Towsner.
The Lebesgue differentiation theorem has many formulations, but we will avoid the strongest versions and just stick to the following model case for simplicity:
Lebesgue differentiation theorem. If
is Lebesgue measurable, then for almost every
we have
. Equivalently, the fundamental theorem of calculus
is true for almost every x in [0,1].
Here we use the oriented definite integral, thus . Specialising to the case where
is an indicator function, we obtain the Lebesgue density theorem as a corollary:
Lebesgue density theorem. Let
be Lebesgue measurable. Then for almost every
, we have
as
, where |A| denotes the Lebesgue measure of A.
In other words, almost all the points x of A are points of density of A, which roughly speaking means that as one passes to finer and finer scales, the immediate vicinity of x becomes increasingly saturated with A. (Points of density are like robust versions of interior points, thus the Lebesgue density theorem is an assertion that measurable sets are almost like open sets. This is Littlewood’s first principle.) One can also deduce the Lebesgue differentiation theorem back from the Lebesgue density theorem by approximating f by a finite linear combination of indicator functions; we leave this as an exercise.
The Lebesgue differentiation and density theorems are qualitative in nature: they assert that eventually gets close to f(x) for almost every x, or that A will eventually occupy most of [x-r,x+r] for almost every x in A, by taking r small enough, but does not give a quantitative bound for how small r has to be. The following simple example shows why there is a problem. Let n be a large integer, and partition [0,1] into
dyadic intervals
(never mind about the overlaps on the boundary, as they have zero measure, and the Lebesgue philosophy in analysis is to always ignore anything which happens on sets of measure zero). Let
be the union of every other interval:
One then sees that if x is any element of which is not on the boundary, then it is indeed true that the local density
of
will eventually converge to 1, but one has to wait until r is of size
or smaller before one sees this; for scales much larger than this, the local density will remain stubbornly close to 1/2. A similar phenomenon holds for the indicator functions
: the local average
will eventually get close to
, which is either 0 or 1, but when
, these averages will also stay close to 1/2. (Closely related to this is the fact that the functions
converge weakly to 1/2, despite only taking values in {0,1}.)
Intuitively, what is going on here is that while each set is certainly Lebesgue measurable, these sets are getting increasingly “less measurable” as n gets large, and the rate of convergence in the Lebesgue differentiation and density theorems depends on how measurable the sets
are. One can illustrate this by considering (non-rigorously) the limiting case
as follows. Suppose we select a random subset
of [0,1] by requiring each real number x in [0,1] to lie in
with an independent probability of 1/2 (thus we are flipping an uncountable number of coins to determine this set!). The law of large numbers (applied very non-rigorously!) then suggests that with probability 1,
should have density 1/2 in every single interval I in [0,1], thus
. This would seem to violate the Lebesgue density theorem; but what is going on here is that the set
is in fact almost surely non-measurable (indeed, the Lebesgue density theorem provides a proof of this fact, modulo the issues of justifying several non-rigorous claims in this paragraph).
So, it seems that to proceed further we need to quantify the notion of measurability, in order to decide which sets or functions are “more measurable” than others. There are several ways to make such a quantification. Here are some typical proposals:
Definition. A set
is
-measurable if there exists a set B which is the union of dyadic intervals
at scale
, such that A and B only differ on a set of Lebesgue measure (or outer measure)
.
Definition. A function
is
-measurable if there exists a function g which is constant on the dyadic intervals
, which differs from f in
-norm by at most
, thus
.
(One can phrase these definitions using the -algebra generated by the dyadic intervals of length
; we will not do so here, but these
-algebras are certainly underlying the ideas here. Their presence is particuarly prominent in the “ergodic theory” approach to this circle of ideas, which we are not focusing on here.)
Then one can obtain the following quantitative results:
Quantitative Lebesgue differentiation theorem. Let
be
-measurable. Then for all x in [0,1] outside of a set of measure
we have
for all
.
Quantitative Lebesgue density theorem. Let
be
-measurable. Then for all x in A outside of a set of measure
we have
for all
.
These results follow quickly from the Hardy-Littlewood maximal inequality, and by exploiting the low “complexity” of the structured objects B and g which approximate A and f respectively; we omit the standard arguments.
To connect these quantitative results back to their qualitative counterparts, one needs to connect the quantitative notion of -measurability with the traditional qualitative notion of Lebesgue measurability. The relevant result that provides this connection is
Lebesgue approximation theorem, first version. Let
be measurable. Then for every
there exists n such that A is
-measurable.
Lebesgue approximation theorem, second version. Let
be measurable. Then for every
there exists n such that f is
-measurable.
These two results are easily seen to be equivalent. Let us quickly recall the proof of the first version:
Proof. The claim is easily verified when A is the finite union of dyadic intervals, and then by monotone convergence one also verifies the claim when A is compact (or open). One then verifies that the claim is closed under countable unions, intersections, and complements, which then gives the claim for all Borel-measurable sets. The claim is also obviously true for null sets, and thus true for Lebesgue-measurable sets.
So, we’re done, right? Well, there is still an unsatisfactory issue: the Lebesgue approximation theorems guarantee, for any given , that a measurable set A or a measurable function f will eventually be
-measurable by taking n large enough, but don’t give any bound as to what this n will be. In a sense, this is unavoidable, even if we consider “nice” objects such as compact sets A or piecewise constant functions f; the example of the set
or the function
discussed previously show that for fixed
, one can be forced to take n to be arbitrarily large.
However, we can start looking for substitutes for these theorems which do have quantitative bounds. Let’s focus on the first version of the Lebesgue approximation theorem, and in particular in the case when A is compact. Then, we can write , where
is the union of all the (closed) dyadic intervals which intersect A. The measures
are a monotone decreasing sequence of numbers between 0 and 1, and thus (by the infinite convergence principle!) they have a limit, which (by the upper continuity of Lebesgue measure) is just
. Thus, for every
we have
for all sufficiently large n, which explains why A is
-measurable for all large n.
So now we see where the lack of a bound on n is coming from – it is the fact that the infinite convergence principle also does not provide an effective bound on the rate of convergence. But in the previous posting on this topic, we saw how the finite convergence theorem did provide an effective substitute for the infinite convergence principle. If we apply it directly to this sequence , this is what we get:
Effective Lebesgue approximation theorem. Let
be any function, and let
. Then there exists an integer N with the following property: given any subset A of [0,1], there exists
such that
is
-measurable.
This theorem does give a specific upper bound on the scale n one has to reach in order to get quantitative measurability. The catch, though, is that the measurability is not attained for the original set A, but instead on some discretisation of A. However, we can make the scale at which we are forced to discretise to be arbitrarily finer than the scale at which we have the measurability.
Nevertheless, this theorem is still a little unsatisfying, because it did not directly say too much about the original set A. There is an alternate approach which gives a more interesting result. In the previous results, the goal was to try to approximate an arbitrary object (a set or a function) by a “structured” or “low-complexity” one (a finite union of intervals, or a piecewise constant function), thus trying to move away from “pseudorandom” or “high-complexity” objects (such as the sets and functions
discussed earlier). Of course, the fact that these pseudorandom objects actually exist is what is making this goal difficult to achieve satisfactorily. However, one can adopt a different philosophy, namely to embrace both the structured and the pseudorandom aspects of these objects, and focus instead on creating an efficient decomposition of arbitrary objects into the structured and pseudorandom components.
To do this, we need to understand what “pseudorandom” means. One clue is to look at the examples and
discussed earlier. Observe that if one averages
on any reasonable sized interval J, one gets something very close to the global average of
, i.e. 1/2. In other words, the integral of
on an interval J is close to the global average of
times
. (This is also true when J is a small interval, since in this case both expressions are small.) This motivates the following definition:
Definition. A function
is said to be
-regular on a dyadic interval I if we have
for all dyadic subintervals
.
Thus, for instance, is
-regular on [0,1]. We then have an analogue of the Szemerédi regularity lemma for subsets of the interval, which I will dub the “Lebesgue regularity lemma”:
Lebesgue regularity lemma. If
and
is measurable, then there exists an positive integer
(i.e. n is bounded by a quantity depending only on
), such that f is
-regular on all but at most
of the
dyadic intervals of length
.
Proof. As with the proof of many other regularity lemmas, we shall rely primarily on the energy increment argument (the energy is also known as the index in some literature). For minor notational reasons we will take to be a negative power of 2. For each integer n, let
be the conditional expectation of f to the dyadic intervals of length
, thus on each such interval I,
is equal to the constant value
(again, we are ignoring sets of measure zero). An easy application of Pythagoras’s theorem (for
) shows that the energies
are an increasing sequence in n, and bounded between 0 and 1. Applying (a special case of) the finite convergence principle, we can find
such that we have the energy metastability
(Indeed, we obtain a fairly civilised bound of ). Applying Pythagoras’ theorem again, we conclude
which by Markov’s inequality implies that
for all but of the
dyadic intervals I of length
. The Cauchy-Schwarz inequality then quickly shows that f is
-regular on all of these intervals.
One can of course specialise the above lemma to indicator functions to obtain a regularity lemma for subsets of the interval, whose formulation I will leave to the reader as an exercise.
An inspection of the proof shows that the full power of the finite convergence principle was not tapped here, because we only used it to get a metastability region of . One can get a stronger result (at the cost of worsening the bound on n) by extending this region of stability. To motivate this stronger version, first observe that if a function f is
-regular on an interval I, then on that interval we have a decomposition f = c+h on I where
is the mean of f on I (in particular, c is constant), and h has small averages in the sense that
for all dyadic subintervals J of I. We can do better than this:
Definition. A function
is said to be strongly
-regular on a dyadic interval I if there exists a decomposition f=c+e+h on I, where
is the mean of f on I, e is small in the sense that
, and h has vanishing averages in the sense that
for all dyadic subintervals
with
.
Note that strong -regularity implies
-regularity as long as
. Strong
-regularity offers much better control on the fluctuation of f at finer scales, as long as the scale is not too fine (this is where the parameter m comes in).
Strong Lebesgue regularity lemma. If
,
, and
is measurable, then there exists an positive integer
such that f is
-regular on all but at most
of the
dyadic intervals of length
.
The bound on n is rather poor, it is basically a -fold iteration of the function
applied to 1, so for instance if one wanted F to be exponential in nature then n might be as large as a tower of exponentials of height
or so. (A very similar situation occurs for the Szemerédi regularity lemma, which has a variety of such strong versions, including one by Alon-Fischer-Krivelevich-Szegedy, one by Rödl-Schacht, and one by myself.)
We can now return to the Lebesgue differentiation theorem, and use the strong regularity lemma to obtain a more satisfactory quantitative version of that theorem:
Quantitative Lebesgue differentiation theorem. If
,
, and
is measurable, then there exists an positive integer
such that for all x in [0,1] outside of a set of measure
we have the Cauchy sequence property
for all
.
This theorem can be deduced fairly easily by combining the strong regularity lemma with the Hardy-Littlewood maximal inequality (to deal with the errors e), and by covering (most of) the non-dyadic intervals [x,x+r] or [x,x+s] by dyadic intervals and using the boundedness of f to deal with the remainder. We leave the details as an exercise.
One sign that this is a true finitary analogue of the infinitary differentiation theorem is that this finitary theorem implies most of the infinitary theorem; namely, it shows that for any measurable f, and almost every x, the sequence is a Cauchy sequence as
, although it does not show that the limit is equal to f(x). (Finitary statements can handle Cauchy sequences – which make sense even in the rationals – but have some trouble actually evaluating the limits of such sequences – which need the (infinite precision) real numbers and thus not truly finitary.) Conversely, using weak compactness methods one can deduce the quantitative differentiation theorem from the infinitary one, in much the same way that the finite and infinite convergence principles can be deduced from each other.
The strong Lebesgue regularity lemma can also be used to deduce the (one-dimensional case of the) Rademacher differentiation theorem, namely that a Lipschitz continuous function from [0,1] to the reals is almost everywhere differentiable. To see this, suppose for contradiction that we could find a function g which was Lipschitz continuous but failed to be differentiable on a set of positive measure, thus for every x in this set, the (continuous) sequence is not a Cauchy sequence as r goes to zero. We can normalise the Lipschitz constant of g to equal 1. Then by standard arguments we can find
and a function
such that for every x in a set of measure greater than
, and every n, the sequence
fluctuates by at least
in the range
. Now let M be a very large integer (depending on
and F) and discretise g to scale
to create a piecewise linear approximant
, which is the antiderivative of a bounded function f which is constant on dyadic intervals of length
. We apply the strong Lebesgue regularity lemma to f and find a scale
for which the conclusion of that lemma holds; by choosing n large enough we can ensure that
. It is then not hard to see that the lemma contradicts the previous assertion that
fluctuates for certain ranges of x and r.
In my next post I will talk about a new paper of mine using some of these ideas to establish a quantitative version of the Besicovitch projection theorem.
[Update, June 19: Definition of strong regularity corrected.]

16 comments
Comments feed for this article
18 June, 2007 at 4:02 pm
Top Posts « WordPress.com
[…] The Lebesgue differentiation theorem and the Szemeredi regularity lemma This post is a sequel of sorts to my earlier post on hard and soft analysis, and the finite convergence principle. […] […]
19 June, 2007 at 6:41 am
Doug
As I understand infinity [oo], reciprocity of limit theory allows this definition of infinity oo := 1/0.
Does reciprocity allow your arguments to be true for the interval [1,oo]?
This seems possible from my visual interpretation the illustration in the section ‘As a sphere’ of ‘Riemann sphere’ using 1 as the equator and 0,oo as the poles.
http://en.wikipedia.org/wiki/Riemann_sphere
19 June, 2007 at 8:19 am
Terence Tao
Dear Doug,
The map x -> 1/x from [0,1] to [1,\infty] preserves the topological structure (such as limits), and in the case of the Riemann sphere, it also preserves the conformal structure (such as angles). But it does not preserve the measure or metric structure (there is a non-trivial Jacobian involved which distorts lengths and measures). So the results do not extend automatically.
Nevertheless, there are various analogues available in infinite-measure settings such as the real line, but one needs an additional decay hypothesis, for instance that the function f is absolutely integrable or that the set A has bounded measure. Also, instead of working with a decomposition into equally spaced intervals, it becomes more effective to work with unequally spaced intervals which are more adapted to where the function or set is distributed; in particular, the Calderon-Zygmund decomposition from harmonic analysis becomes very useful.
19 June, 2007 at 11:04 am
A quantitative form of the Besicovitch projection theorem via multiscale analysis « What’s new
[…] the multiscale arguments used to establish various forms of the Lebesgue differentiation theorem in my previous post (in particular, the finite convergence principle, in the guise of pigeonholing in scales, plays an […]
21 June, 2007 at 9:42 am
Jeremy Avigad
A theorem due to Steinhaus states that if A and B are subsets of the real line with positive Lebesgue measure, then the sumset A + B includes an interval.
Steinhaus originally stated the theorem in terms of distance sets, i.e. replacing B by -B. The article appeared in 1920 in the first volume of Fundamenta Mathematicae, and is available online:
http://matwbn.icm.edu.pl/spis.php?wyd=1
(To whet readers’ curiosity and encourage them to follow the link, I’ll note that 14 of the 24 papers in this first volume were written (or co-written, in one case) by a single person.)
Steinhaus’s theorem is not difficult to prove using the Lebesgue density theorem. But I first learned of it in a paper by Renling Jin, called “Sumset phenomenon” (Proceedings of the AMS, 2001; also available on Jin’s web page), where the result is obtained as an easy corollary of a theorem of nonstandard analysis. (Jin used his nonstandard result to show that if A and B are two subsets of the natural numbers with positive upper Banach density, then A + B is piecewise syndetic, and he has since gone on to make much more extensive use of nonstandard analysis in additive number theory.) Around that time, I developed a syntactic translation of nonstandard proofs to standard ones, and I decided to try it out on Jin’s proof of Steinhaus’s theorem.
With a little heuristic fiddling, I was able to find a constructively valid version of Steinhaus’s theorem, and a direct combinatorial proof. These are described on slides 9-13 of a short talk I gave a few years ago:
Click to access dagstuhl.pdf
The argument follows a strategy mentioned in Tao’s post: the sets A and B are approximated from above by unions of the dyadic intervals that intersect them.
The translation for nonstandard arguments that I mentioned above is described in a paper called “Weak theories of nonstandard arithmetic and analysis,” and perhaps more perspicuously in Section 5.2 of a survey called “Forcing in proof theory,” both available on my web page. (It is also described on the slides at the link above.) Towsner and I have wondered whether the translation might provide a useful aid to “finitizing” methods of analysis. We are looking forward to following up on the topics that have been raised in this thread, as well as the paper by Elek and Szegedy.
21 June, 2007 at 10:11 am
Terence Tao
Dear Jeremy,
Thanks for your commentary and links. I think one can use the quantitative Lebesgue approximation theorem mentioned above to get a similarly quantitative version of Steinhaus’ theorem, which goes something like this: if A, B are measurable subsets of [0,1] of measure at least , and F is any function from the natural numbers to the natural numbers, then there exists a dyadic interval I in [0,2] of some length
, and F is any function from the natural numbers to the natural numbers, then there exists a dyadic interval I in [0,2] of some length 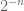 such that A+B is “fills out I at scale
such that A+B is “fills out I at scale 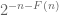 ” in the sense that any dyadic subinterval J of I of length
” in the sense that any dyadic subinterval J of I of length 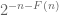 has non-empty intersection with A+B. Furthermore, one can get a uniform bound on n which depends only on
has non-empty intersection with A+B. Furthermore, one can get a uniform bound on n which depends only on  and F; these types of uniformity properties tend to be quite useful in applications (in particular, there are many applications of the Szemeredi regularity lemma which rely crucially on this type of uniform bound on the complexity), and seem to arise whenever the result one is finitising enjoys some sort of “weak compactness”.
and F; these types of uniformity properties tend to be quite useful in applications (in particular, there are many applications of the Szemeredi regularity lemma which rely crucially on this type of uniform bound on the complexity), and seem to arise whenever the result one is finitising enjoys some sort of “weak compactness”.
14 October, 2008 at 8:45 am
Non-measurable sets via non-standard analysis « What’s new
[…] math.LO | Tags: Lebesgue density theorem, measurability, non-standard analysis | by Terence Tao Last year on this blog, I sketched out a non-rigorous probabilistic argument justifying the following well-known theorem: […]
16 October, 2010 at 8:29 pm
245A, Notes 5: Differentiation theorems « What’s new
[…] with a reasonable modulus of continuity, due to the increasingly oscillatory nature of . See this blog post for some further discussion of this issue, and what quantitative substitutes are available for such […]
3 November, 2010 at 6:51 pm
Asymptotic decay for a one-dimensional nonlinear wave equation « What’s new
[…] A compactness argument allows one to extract a quantitative estimate from this theorem (cf. this earlier blog post of mine) which, roughly speaking, tells us that there are large portions of the trajectory which behave […]
27 March, 2012 at 12:34 pm
Jana Rodriguez Hertz
Hi Terence,
what’s the exponent of \varepsilon in the higher dimension version of the Quantitative Lebesgue density theorem? do you obtain the limit is 1-o(\sqrt(\varepsilon)) too? thank you, Jana
27 March, 2012 at 12:40 pm
Jana Rodriguez Hertz
sorry, I shouldn’t have said the limit. I’m interested in the dependence r(\varepsilon) for higher dimension. that is, is there any information (perhaps adding hypothesis) on which r one has to take in order to obtain
|A \cap B_r(x)|> 1-\varepsilon |B_r(x)| ?
that’s it, sorry, and thanks
21 October, 2018 at 4:27 pm
The Inscribed Square Problem | Gödel's Lost Letter and P=NP
[…] if has positive measure, then almost all points in have the density-1 property. Here is a nice comment on this from Terry Tao’s […]
15 August, 2019 at 11:32 am
Quantitative bounds for critically bounded solutions to the Navier-Stokes equations | What's new
[…] of compactness by more complicated substitutes that give effective bounds; see for instance these previous blog posts for more discussion. I therefore was interested in trying to obtain a quantitative […]
12 February, 2020 at 12:07 am
Bob
Hi Terence, by a finite linear combination of indicator functions, say
by a finite linear combination of indicator functions, say  , did you plan to use a weak-(1,1) estimate for the maximal function raising from
, did you plan to use a weak-(1,1) estimate for the maximal function raising from 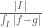 ? I’m asking since I’m wondering if this claim holds true also in the generalized context of complete separable metric spaces equipped with a probability measure, where in general we can’t rely on Besicovitch covering theorem to get the weak-(1,1) estimate…
? I’m asking since I’m wondering if this claim holds true also in the generalized context of complete separable metric spaces equipped with a probability measure, where in general we can’t rely on Besicovitch covering theorem to get the weak-(1,1) estimate…
when you claimed that we can deduce the Lebesgue differentiation theorem back from the Lebesgue density theorem by approximating
Thanks,
Bob
12 February, 2020 at 4:44 am
Bob
I found in the literature that density theorem is equivalent to weak Vitaly property while the differentiation theorem is equivalent to strong Vitaly property and that there exists a complete separable metric space and a finite Borel measure where the weak property holds while the strong doesn’t… so, to answer my own question: in the context of complete separable metric spaces the equivalence between density theorem and differentiation theorem doesn’t hold true.
18 May, 2021 at 1:52 pm
Alan Chang
In the last two displayed equations of the proof of the Lebesgue regularity lemma, the left absolute value bar and the integral sign should be swapped.
[Corrected, thanks – T.]