[This post is authored by Gil Kalai, who has kindly “guest blogged” this week’s “open problem of the week”. – T.]
The entropy-influence conjecture seeks to relate two somewhat different measures as to how a boolean function has concentrated Fourier coefficients, namely the total influence and the entropy.
We begin by defining the total influence. Let be the discrete cube, i.e. the set of
vectors
of length n. A boolean function is any function
from the discrete cube to {-1,+1}. One can think of such functions as “voting methods”, which take the preferences of n voters (+1 for yes, -1 for no) as input and return a yes/no verdict as output. For instance, if n is odd, the “majority vote” function
returns +1 if there are more +1 variables than -1, or -1 otherwise, whereas if
, the “
dictator” function returns the value
of the
variable.
We give the cube the uniform probability measure
(thus we assume that the n voters vote randomly and independently). Given any boolean function f and any variable
, define the influence
of the
variable to be the quantity
where is the element of the cube formed by flipping the sign of the
variable. Informally,
measures the probability that the
voter could actually determine the outcome of an election; it is sometimes referred to as the Banzhaf power index. The total influence I(f) of f (also known as the average sensitivity and the edge-boundary density) is then defined as
Thus for instance a dictator function has total influence 1, whereas majority vote has total influence comparable to . The influence can range between 0 (for constant functions +1, -1) and n (for the parity function
or its negation). If f has mean zero (i.e. it is equal to +1 half of the time), then the edge-isoperimetric inequality asserts that
(with equality if and only if there is a dictatorship), whilst the Kahn-Kalai-Linial (KKL) theorem asserts that
for some k. There is a result of Friedgut that if
is bounded by A (say) and
, then f is within a distance
(in
norm) of another boolean function g which only depends on
of the variables (such functions are known as juntas).
Now we define the entropy. For this we recall the Fourier-Walsh expansion
of any real-valued function , where
is the monomial boolean function
and is the Fourier-Walsh coefficient
Algebraically, the Fourier-Walsh expansion regards f as a polynomial combination of multilinear (square-free) monomials. It is of course a special case of the more general concept of a Fourier transform on an abelian group.
From Plancherel’s theorem we have
The influence can be written similarly:
.
Note that this (together with Plancherel’s theorem) already implies the edge-isoperimetric inequality. The influence thus measures the average “height” of the spectrum, with each set S being viewed as having height |S|.
The spectral entropy E(f) of a boolean function f is defined as
Roughly speaking, it measures the logarithm of the “width” of the Fourier transform of f; it is larger when the spectrum of f is “smeared out”. From Jensen’s inequality, the entropy is at least zero (with equality attained if and only if f is a monomial for some S), and can be as large as n or so (this is the case for random functions, for instance).
Entropy/influence conjecture (Friedgut-Kalai, 1996) : We have
(i.e.
for some absolute constant C.)
Comparing the Fourier-analytic formulae for the entropy and influence, we thus see that this conjecture asserts in some sense that if the Fourier coefficients are “smeared” then the Fourier coefficients are (on average) “high”. One strange feature of this conjecture is worth noting: the spectral entropy is invariant under arbitrary linear transformations, whereas the influence depends on a specific basis. Thus, the conjecture also implies that if Fourier coefficients are smeared, then they are high with respect to arbitrary bases.
On the other hand, both the entropy and influence are additive with respect to tensor products: if and
are boolean functions, then the tensor product
is such that
and
. This fact is of course consistent with the conjecture.
The entropy/influence conjecture, if true, has several consequences:
- Influences under symmetry. The motivation for the entropy/influence conjecture was to understand influences (and the related threshold behavior) under symmetry. Here is a simple case: suppose that f is symmetric under some transitive group of permutations acting on the variables. Suppose also that f is odd (i.e.
). In terms of voting methods, this means that the two candidates +1, -1 are treated equally, and that every individual voter is treated equally, though because we do not assume that the permutation group is 2-transitive, it is not necessarily the case that every pair of voters is treated equally.The entropy/influence conjecture then implies a lower bound of
. An unconditional proof of this latter claim was obtained by Friedgut and Kalai using the KKL theorem mentioned earlier.For certain specific types of permutation groups, the entropy/influence conjecture predicts a precise improvement of this logarithmic lower bound. Slightly weaker versions of these improved bounds were established by Bourgain and Kalai, and
interesting to see if the techniques extend to give some weaker form of the conjecture without symmetry.
Results about influence under symmetry give some hope
for similar results on influences under some sort of “spectral continuity” hypothesis. Roughly speaking, one expects assertions of the form “When the variables have geometric meaning and the Fourier coefficients respect the geometry and are “continuous”, then the influence must be high.” - Mansour’s conjecture. Consider a Boolean function f described by a formula in conjunctive normal form of polynomial size in n. Yishay Mansour conjectured (see also this paper) that most of the Fourier coefficients are concentrated only on
polynomial number of coefficients! This conjecture is still open. Using a theorem of Hastad and Boppana one can show; thus Mansour’s conjecture will follow from the entropy/influence conjecture. Mansour’s motivation was to show that such Boolean functions can be statistically learned (for uniform random input) in polynomial time. This was proved by Jackson using a different method.
There are some variants and strengthenings of this conjecture:
- Other probability distributions. The notions considered here and the entropy/influence-conjecture extend if we replace the unbiased Boolean variables with other product probability spaces, such as independent biased Boolean variables or Gaussian variables. It is also of interest to consider non-product spaces as well.
- Noise sensitivity versions. The entropy/influence conjecture shows that the mean height of the spectrum is
. Can one guarantee a more robust conclusion, namely that the median height (or other percentiles) are also
? (This is called “noise sensitivity” but I will not explain why.) This claim is not true for the majority vote function, but some version of this may persist if one somehow rules out majority vote-like examples – for instance by considering boolean functions which are monotone, invariant under a transitive permutation group, with influence
(say).
- Pivotals distribution versions. If f is a boolean function and
, define
. If x is selected randomly, then
is a random subset of
; the distribution of this random variable is called the pivotals distribution. Note that the expected value of this distribution is precisely I(f), so the pivotals distribution is somewhat analogous to the spectral distribution. We can ask if some version of the influence/entropy inequality applies also here. (A direct translation fails for the majority function, so we will need a weaker form.) Existence of such connection gives interesting prediction for pivotal sets for certain interesting examples.
- Matrix function versions. The following related conjecture is based on discussions together with Itai Benjamini, Gadi Kozma, Elchanan Mossell, and Ofer Zeitouni.
Conjecture. There is an absolute constant
with the following property. Let
be an odd function on the space
of antisymmetric real
matrices, which is invariant under similarity of matrices. Then we have
, where the influence and
norm are measured using the Gaussian probability distribution on
. [To define the influence of non-boolean functions, one considers the average variance of these functions in each of the coordinates in turn, keeping all the other coordinates frozen.]
Kalai and Safra have a survey on issues related to these conjectures.
[Update, Aug 17: Maths typo corrected. – T.]

25 comments
Comments feed for this article
17 August, 2007 at 1:02 am
otto
Gil,
A small correction: At some point near the middle of your post, you start summing over S a subset of the cube, whereas it should be S a subset of {1,2, …, n}.
The same question can be asked for real-valued functions on the discrete cube, or perhaps for functions taking values in [-1,+1]. Is it essential that the range be discrete?
17 August, 2007 at 6:19 am
John Armstrong
Hi, Dr. Kalai. What I can see looks interesting, but the vast majority of your LaTeX formulas do not parse. I’m digging through the HTML source I see on this end, but I can’t see what’s going wrong. Do you see them rendered properly at your end?
17 August, 2007 at 7:22 am
Ryan O'Donnell
Otto, the range being {-1,1} is essential. Consider , which has range [-1,1]. Then I(f) = 1/n, but
, which has range [-1,1]. Then I(f) = 1/n, but  .
.
Mysteriously, if you define Ent(f) to be the same as E(f) except you don’t put in the “hats” (i.e., you take the entropy of f’s squared values, rather than f’s Fourier coefficients’ squared values), then it holds that . This is the Logarithmic-Sobolev Inequality for {-1,1}^n.
. This is the Logarithmic-Sobolev Inequality for {-1,1}^n.
Gil might also have mentioned the application of this conjecture (and related ideas) to the theory of metric space embeddings; see, e.g., Cor. 3.9 in:
Click to access nonembed-final-new.pdf
17 August, 2007 at 7:30 am
Terence Tao
Otto: Thanks for the typo correction! (For technical reasons, I am the one responsible for these sorts of formatting issues, though Gil is of course responsible for the content.)
John: I see the LaTeX displaying just fine; perhaps there was some temporary wordpress glitch.
17 August, 2007 at 1:40 pm
otto
Is there an entropic uncertainty principle saying that one of Ent(f) or Ent(\hat f) has to be large? (assuming |f| = 1)
17 August, 2007 at 2:50 pm
Terence Tao
Dear Otto,
There is indeed such a principle; in fact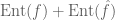 is minimised precisely when f is a sharp example for the discrete uncertainty principle
is minimised precisely when f is a sharp example for the discrete uncertainty principle  (in this context |G| would be 2^n), or in other words when f (and hence
(in this context |G| would be 2^n), or in other words when f (and hence 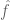 ) is a scalar multiple of a translated and modulated indicator function of a subgroup. Indeed it is not hard to see (from Jensen’s inequality) that the entropy uncertainty principle implies the discrete uncertainty principle.
) is a scalar multiple of a translated and modulated indicator function of a subgroup. Indeed it is not hard to see (from Jensen’s inequality) that the entropy uncertainty principle implies the discrete uncertainty principle.
One particularly slick proof of the entropy uncertainty principle is to take the sharp Hausdorff-Young inequality, which with the right normalisations reads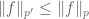 for
for 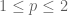 , and differentiate (!) this inequality at
, and differentiate (!) this inequality at 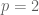 (noting from Plancherel’s identity that we have identity at the endpoint
(noting from Plancherel’s identity that we have identity at the endpoint 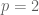 ).
).
17 August, 2007 at 3:59 pm
Top Posts « WordPress.com
[…] (Gil Kalai) The entropy/influence conjecture [This post is authored by Gil Kalai, who has kindly “guest blogged” this week’s “open problem of the week”. – […] […]
17 August, 2007 at 5:31 pm
otto
What about the following question (which seems morally close).
Consider . Do we have
. Do we have
Even more ambitiously, if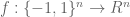 , is one of
, is one of ?
?
Ent(f) or Ent(\hat f) always bounded by
(Either concentrate of measure or concentration of spectral measure?)
18 August, 2007 at 9:42 pm
Gil Kalai
Dear all, Greetings from Jerusalem. Thanks everybody for the interesting comments, suggestions and corrections, and thanks Terry for hosting me so helpfully.
I think that Otto’s idea to find a version of the E/I-conjecture for real functions on the discrete cube is a good idea but I do not know how to do it. (As Ryan pointed out we need to modify the formulation.) Let me mention a formula by Michel Talagrand (formula (1.2) in the paper: On Russo’s approximate zero-one law, Ann. of Prob. 22 (1994) 1576-1578,) which extends the KKL Theorem (in a sharp form) to arbitrary real functions on the discrete cube.
(I did not understand Otto’s suggestion from remark 8 regarding functions from the discrete -dimensional cube to
-dimensional cube to 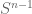 and
and 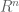 . Is it important that the
. Is it important that the  on both sides is the same? Also please remind me what is the LIP norm.)
on both sides is the same? Also please remind me what is the LIP norm.)
The connection to metric embeddings that Ryan mentioned is indeed a very nice recent application of Fourier analysis of Boolean functions (along with a lot of other stuff). Subash Khot and Nisheeth Vishnoi made the breakthrough proving that there is a finite metric space of size in
in  which requires a distortion of
which requires a distortion of 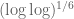 for
for  -embedding. (46th Annual IEEE Symposium on Foundations of Computer Science (FOCS’05) pp. 53-62.) Their result answered negatively a fundamental problem posed by Goemans and Linial. Along with Muli Safra we spent a lot of efforts to understand their beautiful paper. And we even have some hopes that the E/I conjecture or some relative may be relevant for possible improvements.
-embedding. (46th Annual IEEE Symposium on Foundations of Computer Science (FOCS’05) pp. 53-62.) Their result answered negatively a fundamental problem posed by Goemans and Linial. Along with Muli Safra we spent a lot of efforts to understand their beautiful paper. And we even have some hopes that the E/I conjecture or some relative may be relevant for possible improvements.
19 August, 2007 at 8:30 pm
Hamed Hatami
Let me mention a problem due to Ryan O’Donnell which is related to
the entropy/influence conjecture. The following statement follows
immediately from the conjecture, but a valid proof that does not use
the conjecture is unknown.
There exists a positive constant such that the following
such that the following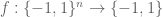 , then
, then
holds. If
When is monotone, the statement follows from the KKL
is monotone, the statement follows from the KKL .
.
theorem as in that case
14 March, 2008 at 12:09 am
Gil Kalai
I realized a typo in my presentation. In the four displaced formulas where the sums are over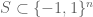 , it should be, of course, over
, it should be, of course, over  .Sorry!
.Sorry!
Here is another remark: Item 3 in the “variants” considers the distribution of the sets of pivotals, and asks if the influence is bounded below by a constant times the entropy of this pivotal distribution.
I claimed that this does not work for the balanced majority function, but it does. In this case with probability we have the empty sets as the set of pivotals and otherwise the set of pivotals is a random set of size
we have the empty sets as the set of pivotals and otherwise the set of pivotals is a random set of size ![{}[n/2]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%2F2%5D&bg=ffffff&fg=545454&s=0&c=20201002) or
or ![{}[n/2]+1](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%2F2%5D%2B1&bg=ffffff&fg=545454&s=0&c=20201002) . So it looks that both the influence and entropy of the pivotals distribution is
. So it looks that both the influence and entropy of the pivotals distribution is  .
.
14 May, 2008 at 7:51 am
Combinatorics, mathematics, academics, polemics, … « Combinatorics and more
[…] and the other was about the entropy/influence conjecture. […]
31 May, 2008 at 10:09 am
Nati’s Influence « Combinatorics and more
[…] post: The Entropy Influence Conjecture. (Terry Tao’s blog) Possibly related posts: (automatically generated)Smart Mobs, Dumb […]
31 January, 2009 at 6:36 am
Quantum boolean functions « Tobias J. Osborne’s research notes
[…] than review the theory of fourier analysis for boolean functions I’ll just refer you to the post by Gil Kalai on the entropy influence conjecture which contains a very readable account. […]
16 October, 2009 at 5:45 pm
Analysis and Probability of Boolean Functions — Gil Kalai at the UCLA-IPAM Colloquium « Not just coffee time
[…] on Analysis and Probability of Boolean Functions. Parts of this talk have been featured in a guest blog entry over at Terence Tao’s […]
23 February, 2010 at 2:08 pm
Gil
Mansour’s conjecture for random DNF formulas was proved by Adam Klivans, Homin Lee, Andrew Wan http://eccc.hpi-web.de/report/2010/023/
2 April, 2011 at 4:22 am
Gil Kalai
There is a new paper on the conjecture entitled The Fourier Entropy-Infuence Conjecture
for certain classes of Boolean functions, by
Ryan O’Donnell, John Wright, and Yuan Zhou, that can be found here
Click to access fei.pdf
The paper contains a proof of the conjecture for symmetric Boolean functions and in various other cases. For symmetric functions a noise sensitivity statement for the discrete directional derivatives of the function
which implies the conjecture is proved.
Let me also mention that Gady Kozma asked if the conjecture remains true for functions to the unit circle in the complex plane.
14 December, 2020 at 2:15 am
Gil Kalai
Gideon Schechtman used analogs of the Rudin-Shapiro pairs of functions to find a counter example to the entropy/influence statement for functions to the unit complex circle. https://arxiv.org/abs/2009.12753
14 June, 2011 at 12:53 pm
Tentative Plans and Belated Updates II | Combinatorics and more
[…] theorem in terms of families of fans. (We asked about it here.) There is a new paper on the Entropy-Influence conjecture entitled The Fourier Entropy-Infuence Conjecture for certain classes of Boolean […]
1 November, 2013 at 4:39 am
NatiFest is Coming | Combinatorics and more
[…] post: The Entropy Influence Conjecture. (Terry Tao’s […]
6 March, 2020 at 6:05 am
A new PolyTCS blog! | Combinatorics and more
[…] is a 2014 post on GLL on the problem of Project 2, and here is my 2007 post on WN on the problem of Project […]
6 March, 2020 at 6:14 am
Gil Kalai
Let me mention a substantial progress and a proof of a weaker form of the conjecture in https://arxiv.org/abs/1911.10579 by Esty Kelman, Guy Kindler, Noam Lifshitz, Dor Minzer, and Muli Safra.
22 March, 2020 at 2:43 am
Kelman, Kindler, Lifshitz, Minzer, and Safra: Towards the Entropy-Influence Conjecture | Combinatorics and more
[…] Let me briefly report on a remarkable new paper by Esty Kelman, Guy Kindler, Noam Lifshitz, Dor Minzer, and Muli Safra, Revisiting Bourgain-Kalai and Fourier Entropies. The paper describes substantial progress towards the Entropy-Influence conjecture, posed by Ehud Friedgut and me in 1996. (See this blog post from 2007.) […]
29 January, 2021 at 1:03 am
Possible future Polymath projects (2009, 2021) | Combinatorics and more
[…] are so far three very interesting proposals there, and the first proposal is the Friedgut-Kalai Entropy/Influence conjecture. For various proposals, see also the polymath blog administered by Tim Gowers, Michael Nielsen, […]
27 September, 2021 at 12:25 am
Everyday entropy: what is a map? – bonefactory
[…] https://www.quantamagazine.org/gil-kalais-argument-against-quantum–computers-20180207/ I think that the effort required to obtain a low enough error level for any implementation of universal quantum circuits increases exponentially with the number of qubits, and thus, quantum computers are not possible. I am pretty certain, while a little nervous to be proven wrong. Our results state that noise will corrupt the computation, and that the noisy outcomes will be very easy to simulate on a classical computer. This prediction can already be tested; you don’t even need 50 qubits for that, I believe that 10 to 20 qubits will suffice. For quantum computers of the kind Google and IBM are building, when you run, as they plan to do, certain computational processes, they expect robust outcomes that are increasingly hard to simulate on a classical computer. Well, I expect very different outcomes. So I don’t need to be certain, I can simply wait and see. https://terrytao.wordpress.com/2007/08/16/gil-kalai-the-entropyinfluence-conjecture/#more-41 […]