One of my favourite unsolved problems in mathematics is the Kakeya conjecture in geometric measure theory. This conjecture is descended from the
Kakeya needle problem. (1917) What is the least area in the plane required to continuously rotate a needle of unit length and zero thickness around completely (i.e. by
)?
For instance, one can rotate a unit needle inside a unit disk, which has area . By using a deltoid one requires only
area.
In 1928, Besicovitch showed that that in fact one could rotate a unit needle using an arbitrarily small amount of positive area. This unintuitive fact was a corollary of two observations. The first, which is easy, is that one can translate a needle using arbitrarily small area, by sliding the needle along the direction it points in for a long distance (which costs zero area), turning it slightly (costing a small amount of area), sliding back, and then undoing the turn. The second fact, which is less obvious, can be phrased as follows. Define a Kakeya set in to be any set which contains a unit line segment in each direction. (See this Java applet of mine, or the wikipedia page, for some pictures of such sets.)
Theorem. (Besicovitch, 1919) There exists Kakeya sets
of arbitrarily small area (or more precisely, Lebesgue measure).
In fact, one can construct such sets with zero Lebesgue measure. On the other hand, it was shown by Davies that even though these sets had zero area, they were still necessarily two-dimensional (in the sense of either Hausdorff dimension or Minkowski dimension). This led to an analogous conjecture in higher dimensions:
Kakeya conjecture. A Besicovitch set in
(i.e. a subset of
that contains a unit line segment in every direction) has Minkowski and Hausdorff dimension equal to n.
This conjecture remains open in dimensions three and higher (and gets more difficult as the dimension increases), although many partial results are known. For instance, when n=3, it is known that Besicovitch sets have Hausdorff dimension at least 5/2 and (upper) Minkowski dimension at least . See my Notices article for a general survey of this problem (and its connections with Fourier analysis, additive combinatorics, and PDE), my paper with Katz for a more technical survey, and Wolff’s survey for a systematic treatment of the field (up to about 1998 or so).
In 1999, Wolff proposed a simpler finite field analogue of the Kakeya conjecture as a model problem that avoided all the technical issues involving Minkowski and Hausdorff dimension. If is a vector space over a finite field F, define a Kakeya set to be a subset of
which contains a line in every direction.
Finite field Kakeya conjecture. Let
be a Kakeya set. Then E has cardinality at least
, where
depends only on n.
This conjecture has had a significant influence in the subject, in particular inspiring work on the sum-product phenomenon in finite fields, which has since proven to have many applications in number theory and computer science. Modulo minor technicalities, the progress on the finite field Kakeya conjecture was, until very recently, essentially the same as that of the original “Euclidean” Kakeya conjecture.
Last week, the finite field Kakeya conjecture was proven using a beautifully simple argument by Zeev Dvir, using the polynomial method in algebraic extremal combinatorics. The proof is so short that I can present it in full here.
The polynomial method is used to control the size of various sets E by looking at one or more polynomials P which vanish on that set E. This philosophy of course closely resembles that of algebraic geometry, and indeed one could classify the polynomial method as a kind of “combinatorial algebraic geometry”. An important difference, though, is that in the combinatorial setting we work over fields that are definitely not algebraically closed; in particular, we are primarily interested in polynomials and their zero sets over finite fields. [Also, whereas algebraic geometry is more concerned with specific (and often highly structured) polynomials, the polynomial method requires that one consider rather generic (and usually quite high degree) polynomials.]
For instance, in high school we learn the following connection between one-dimensional sets E, and polynomials P(x) of one variable:
Factor theorem. Let F be a field, and
be an integer. Let
denote the polynomials in one variable with coefficients in F.
- If
is a non-zero polynomial of degree at most d, then the set
has cardinality at most d.
- Conversely, given any set
of cardinality at most d, there exists a non-zero polynomial
of degree at most d that vanishes on E.
Thus, to obtain an upper bound on the size of a one-dimensional set E, it would suffice to exhibit a non-zero low-degree polynomial that vanishes on E; conversely, to lower bound the size of E, one would have to show that the only low-degree polynomial that vanishes on E is the zero polynomial. It is the latter type of observation which is of relevance to the finite field Kakeya problem.
There are analogues of both 1. and 2. above in higher dimensions. For instance, the Schwartz-Zippel lemma is a higher-dimensional analogue of 1, as is the combinatorial nullstellensatz of Alon, while Stepanov’s method exploits a higher-dimensional analogue of 2. (Bézout’s theorem from algebraic geometry also qualifies as a variant of 1.) These sorts of techniques and results are collectively referred to as the polynomial method in extremal algebraic combinatorics. For Dvir’s argument, we will need a very simple higher-dimensional version of 2. that comes from basic linear algebra, namely
Lemma. Let
be a set of cardinality less than
for some
. Then there exists a non-zero polynomial
on n variables of degree at most d which vanishes on E.
Proof. Let V be the vector space of polynomials in of degree at most d. Elementary combinatorics reveals that V has dimension
. On the other hand, the vector space
of F-valued functions on E has dimension
. Hence the evaluation map
from V to
is non-injective, and the claim follows.
Dvir’s argument combines this lemma with
Proposition. Let
be a polynomial of degree at most
which vanishes on a Kakeya set E. Then P is identically zero.
Proof. Suppose for contradiction that P is non-zero. We can write , where
is the degree of P and
is the
homogeneous component, thus
is non-zero. Since P vanishes on E, d cannot be zero.
Let be an arbitrary direction. As E is a Kakeya set, E contains a line
for some
, thus
for all
. The left-hand side is a polynomial in t of degree at most
, and thus vanishes identically by the factor theorem. In particular, the
coefficient of this polynomial, which is
, vanishes for any non-zero v. Since
is homogeneous of degree
,
vanishes on all of
. Since
also has degree less than
, repeated application of the factor theorem for each variable in turn (or the Schwarz-Zippel lemma, which is much the same thing) shows that
, a contradiction.
Remark. The point here is that a low-degree polynomial which vanishes on a line must also vanish on the point at infinity where the line touches the hyperplane at infinity. Thus a polynomial which vanishes on a Kakeya set vanishes at the entire hyperplane at infinity. One can then divide out the defining polynomial for that hyperplane and repeat the process to conclude that the polynomial vanishes identically.
Combining the lemma and the proposition we obtain
Corollary. Every Kakeya set in
has cardinality at least
.
Since , this establishes the finite field Kakeya conjecture.
This bound seems to be quite tight. For instance, it gives the lower bound of for Kakeya sets in
(which was already implicitly observed by Wolff). The best known lower bound currently in this case is
, due to Cooper (see also a related paper by Faber); in the other direction, an example of Mockenhaupt and myself shows that such sets can have cardinality
.
It now seems sensible to revisit other problems in extremal combinatorics over finite fields to see if the polynomial method can yield results there. Certainly close relatives of the Kakeya conjecture (e.g. the Nikodym set conjecture, or the Kakeya maximal function conjecture) should now be establishable by these methods. On the other hand, there are other problems (such as the sum-product problem, Szemerédi-Trotter type theorems, and distance set problems) which are sensitive to the choice of field F (and in particular, whether that field contains a subfield of index 2); see this paper of Bourgain, Katz, and myself for further discussion. It would be interesting to see if there are ways to adapt the polynomial method in order to detect the existence of subfields.
Unfortunately, the polynomial method is extremely dependent on the algebraic nature of the finite field setting and does not seem to extend directly to the Euclidean case (though there may be a chance that they may extend instead to certain problems in discrete combinatorial incidence geometry, such as the “joints” problem of Sharir, perhaps by using various embedding theorems). On the other hand, this result lends significant indirect support to the Euclidean Kakeya conjecture; in particular, the result morally rules out any “algebraic” counterexample to the Euclidean conjecture, since a highly algebraic example to this conjecture would likely be adaptable to the finite field setting. (The examples of zero measure Kakeya sets in the Euclidean plane have no finite field analogue, but they are non-algebraic in nature, and in particular take advantage of the multiple scales available in the Euclidean setting.)
[Update, Mar 24: Proof of proposition expanded.]
[Update, Mar 25: See also these posts by Izabella Laba and Quomodocumque.]

43 comments
Comments feed for this article
24 March, 2008 at 2:05 pm
JSE
Beautiful!
I would certainly call this an argument in algebraic geometry, by the way — algebraic geometers certainly do work over finite fields and not only over their algebraic closures! And arguments like the one presented here, where one shows existence of a polynomial vanishing on some specified set (i.e. a variety passing through some set of points) are quite common, even when the variety is, as you describe it, “generic” and not some specific algebraic set contemplated in advance.
24 March, 2008 at 4:24 pm
Terence Tao
Dear JSE,
Well, you’re much closer to algebraic geometry as it is currently practised than I am, so I will cede the point (my knowledge of the subject sort of stops at the graduate level). It does seem hard to draw a sharp line where the algebraic geometry stops and the combinatorics begins. On the other hand, there does seem to be some differences in emphasis between this type of algebraic extremal combinatorics and more classical algebraic geometry. For instance, in the combinatorial approach one tends to study polynomials individually (except when it is necessary to invoke dimension-counting arguments, as in the above lemma), whereas in classical algebraic geometry one tends to collect polynomials into ideals or rings and manipulate those objects instead. It also seems that many of the fundamental theorems in algebraic geometry (e.g. Hilbert’s nullstellensatz) are not directly useful for combinatorics (due in part to their reliance on algebraic closure, and also because the effective bounds associated with such theorems are sometimes a bit poor), though there are often very useful substitutes (e.g. Alon’s combinatorial nullstellensatz) which can be used instead. Still, the two subjects are definitely extremely close to each other (as I said above, one can certainly classify the polynomial method as belonging to the broader subject of algebraic geometry, even if it does not exactly fit into the classical approach to the subject).
24 March, 2008 at 4:43 pm
carlbrannen
Okay, intuitively I understand the 2-d case. But only by translating it into blue-collar terms. What’s the minimum tread area in which you can turn a forklift 360 degrees? (If you only count area where the front wheels diverge from the paths of the rear wheels or vice versa.) The solution is to not turn the steering wheel much, but to take long cuts.
24 March, 2008 at 7:09 pm
ninguem
There is something missing in the proof of the proposition. You proved that P_d vanishes for all v nonzero in F^n. That is not the same as P_d being identically zero since F is finite. I guess that should follow from d < |F| but is not automatic.
24 March, 2008 at 7:15 pm
Terence Tao
Good point; I’ve amended the proof of the proposition accordingly.
25 March, 2008 at 7:32 am
Give the people (who like the Kakeya problem) what they want « Quomodocumque
[…] the people (who like the Kakeya problem) what they want 25Mar08 Wow — make one comment on Terry’s blog and you get a ton of […]
26 March, 2008 at 6:30 am
JSE
Here’s another question, in the vein of “how seriously should we take the analogy between the finite field situation and the Euclidean situation”?
(as usual, all math here is done on the fly and should not be considered checked.)
Suppose that you fix some constants c_n and consider subsets S of F_q^n with cardinality at most c_n q^d; is this what you would take as a model for a subset of R^n with Hausdorff dimension at most d?
Now one can find a polynomial f of degree on order q^{d/n} vanishing on S.
Let L be a line intersecting S in more than q^{d/n} points. Then f must vanish identically on L. So f also vanishes at the intersection of L with H, the hyperplane at infinity.
As in Dvir’s argument we can represent f projectively by a homogeneous form of degree at most q^{d/n} which doesn’t vanish identically on H. So its vanishing on H is contained in a hypersurface of degree at most q^{d/n}, which should have at most q^{n -2 + d/n} points or so. So this is an upper bound for the number of directions in which there exists a line with “excess intersection” with S in this sense.
So here’s a question — Let S be a subset of R^n of Hausdorff dimension d, and let D be the set of directions in which there exists a line L such that L intersect S has Hausdorff dimension greater than d/n. Do you expect it to follow that D has Hausdorff dimension at most n-2+d/n?
This evidently implies the Kakeya conjecture; do you see it as essentially the same, or is this a much stronger statement?
26 March, 2008 at 9:14 am
Terence Tao
The standard conjecture for this is the Kakeya maximal function conjecture. Ignoring factors of , the finite field version of this conjecture is the following: if S is a set and D is a set of directions in which there exists a line L that intersects S in at least k points, then
, the finite field version of this conjecture is the following: if S is a set and D is a set of directions in which there exists a line L that intersects S in at least k points, then
The Kakeya set conjecture essentially corresponds to the case in which and
and  . Other extreme cases include the case
. Other extreme cases include the case 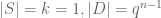 (a point) and
(a point) and  (a line).
(a line).
In Euclidean space, the analogue of the conjecture is as follows: if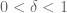 , S is a
, S is a  -separated set in
-separated set in 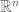 and D is a
and D is a  -separated set of directions in which there exists a unit line segment which comes within
-separated set of directions in which there exists a unit line segment which comes within  of at least k points in S, then
of at least k points in S, then
(i.e.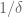 basically plays the role of q in the Euclidean case). Morally speaking (ignoring technicalities regarding the distinction between Hausdorff dimension, lower Minkowski dimension, and upper Minkowski dimension), (**) implies that
basically plays the role of q in the Euclidean case). Morally speaking (ignoring technicalities regarding the distinction between Hausdorff dimension, lower Minkowski dimension, and upper Minkowski dimension), (**) implies that
whenever D is a family of lines which intersect S in a set of dimension s.
The estimate (**) is best possible in all parameter ranges, as one can see by considering examples in which S is a ball or a tube. (It is not however believed that (***) is sharp; there is a conjecture of Wolff on this relating to “Furstenberg sets”, and in fact a paper of myself and Nets Katz, combined with a “discretised sum-product theorem” of Bourgain, gives a tiny improvement to (***) in the case n=2, s=1/2, dim(D)=1.) However, it appears that (*) is only sharp at certain discrete parameter regimes, e.g. E needs to be an integer power of d. Your argument suggests there is in fact some sharp transition phenomena, e.g. if and
and  then one expects only the trivial bound
then one expects only the trivial bound  when c is a small constant (consider for instance the case d=0), but you obtain the refinement
when c is a small constant (consider for instance the case d=0), but you obtain the refinement 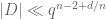 when c is a large constant.
when c is a large constant.
So it looks like your argument should be able to not only establish the Kakeya maximal function conjecture in the finite field case, but even indicate some parameter ranges in which an improvement is possible! But such improvement would definitely be a phenomenon specific to finite fields.
The survey article of Wolff mentioned in the main post is perhaps still the best reference for these things, in case you want to know more.
26 March, 2008 at 5:43 pm
carlbrannen
As I figured out while driving over to the airport, my comment on understanding the 2-d case intuitively is completely wrong. Let me try and make a better intuitive explanation.
(1) Suppose instead of turning the needle around its center, you pick a point perpendicular to the needle and swing the needle around that point. This will sweep out an annulus. As the point you sweep around gets farther from the needle, the annulus gets thinner, but longer. It turns out that these two effects cancel, the area stays the same (at least to first order).
(2) When you rotate the needle by x radians, you inevitably sweep out an area of . To make the total area swept out be small, you have to arrange the swept areas so that they overlap. This is very non intuitive.
. To make the total area swept out be small, you have to arrange the swept areas so that they overlap. This is very non intuitive.
27 March, 2008 at 1:48 am
Nikolay Vereshchagin
I have a question related to Kakeya’s sets and proofs of Kakeya’s conjecture.
Let L be a collection of lines in F^n such that L has exactly one line going in each direction (thus L has about |F|^{n-1} lines).
Let E stand for the Kakeya set consisting of all points in lines from L.
Consider the following random variable X_L in E: we pick at random a line in L and output a random point lying on that line. The Shannon entropy H(X_L) of this random variable is at most log |E|. We need a lower bound for H(X_L). My question is: is it always true that H(X_L) is about n log|F| (say, up to an additive O(n log log |F|) term)? The truth of Kakeya’s
conjecture gives a hope that this might be true.
We need an answer to this question
to analyse our “geometric” protocol to generate strings of large Shannon entropy (http://lpcs.math.msu.su/~ver/papers/rsf.pdf)
Previously, we used Gerd and Tao’s proof of the lower bound |E|>|F|^{n/2+1} and showed that H(X_L)>(n/2+1)log|F|.
I do not see how to use Dvir’s arguments.
27 March, 2008 at 3:25 am
Zeev Dvir
To Nikolay,
It is possible to prove the claim that you stated using a similar argument to the one I used for Kakeya sets. It actually shows that X_L is close to having min-entropy (1-eps)*n*log(q) for every eps>0 (provided q >~ n^{1/eps}).
This argument (in a slightly more complicated setting, involving curves) will appear soon in a paper I am writing with Avi Wigderson (the paper deals with application to the construction of randomness extractors).
Best,
Zeev.
27 March, 2008 at 6:15 pm
harrison
Prof. Tao (or Mr. Dvir, whoever can answer),
It was pointed out to me that the argument is fairly similar to the encryption/decryption algorithms for Reed-Solomon codes. Is this coincidental, is it just a consequence of the polynomial method, or is there a deeper connection that I’m missing?
Thanks,
Harrison
1 April, 2008 at 3:03 pm
Gil Kalai
(Wow!!)
Is there an analog to the finite Kakeya problems for more combinatorial notions of the term “lines” like those used in the Hales-Jewett theorem?
1 April, 2008 at 3:51 pm
Terence Tao
Dear Harrison,
One can certainly interpret this proof in coding language; the proposition in the post can be viewed as an assertion that a Reed-Solomon code of a certain order can be uniquely decoded by looking at the restriction of that code to a Kakeya set, and the Lemma can be viewed as a lower bound on the capacity of that code. I believe that this proof of Kakeya was motivated by some computer science considerations that are somewhat related to coding theory, but I do not know the full details.
Dear Gil: Well, there is of course the density Hales-Jewett theorem of Furstenberg and Katznelson, which (viewed contrapositively) is the assertion that if a set contains a point in every combinatorial line, then it has asymptotically full measure, which is an assertion of a vaguely Kakeya-type nature. Of course, algebraic methods such as the polynomial method are unlikely to apply directly to such a combinatorial situation that has no obvious algebraic structure, but it is still an interesting question as to whether some other proof of the density Hales-Jewett theorem (including, perhaps, a simplified ergodic theory proof) is available.
1 April, 2008 at 5:31 pm
Gil Kalai
Right, but density H-J is only a vaguely Kakeya type question. If you insist on having a “combinatorial line” in each “direction” how large should the set be? (There are various combinatorial notions of lines/direction you can take but as the condition is weaker maybe the set need not be so very large. )
1 April, 2008 at 5:39 pm
Terence Tao
Hmm, now that I think about it, there is a significant difference between finite field Kakeya and HJ. Both take place on a discrete cube![{}[k]^d](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5Ed&bg=ffffff&fg=545454&s=0&c=20201002) (in the finite field case we identify [k] with a finite field). But Kakeya is only non-trivial in the regime when d is fixed and k goes to infinity, while in contrast Hales-Jewett is only interesting in the regime when k was fixed and d goes to infinity. For bounded d the combinatorial lines split into easily understood families and there is not much of interest to say.
(in the finite field case we identify [k] with a finite field). But Kakeya is only non-trivial in the regime when d is fixed and k goes to infinity, while in contrast Hales-Jewett is only interesting in the regime when k was fixed and d goes to infinity. For bounded d the combinatorial lines split into easily understood families and there is not much of interest to say.
From past experience with HJ I would have to say that how one defines the “number” of lines involved is going to be very important; a naive notion of cardinality is probably not the right one (it assigns too much weight to those lines with about half of the coordinates being active). A randomly formulated problem in this area is likely to be either trivially true, trivially false, or otherwise not terribly interesting.
2 April, 2008 at 6:11 am
Gil
Dear Terry,
One nice problem for practicing discretization+polynomial method or other methods is this: What is the largest measure of a subset of the
of the  -sphere which does not contain two orthogonal vectors. a natural guess is the twice the measure of a spherical cup of radius
-sphere which does not contain two orthogonal vectors. a natural guess is the twice the measure of a spherical cup of radius 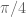 . When
. When  is large this is roughly a fraction
is large this is roughly a fraction  of the total measure of the sphere.
of the total measure of the sphere.
Now, the corresponding problem for the discrete cube (when the dimension is 4 times a prime number) can be solved (up to a factor 2 or so) by the polynomial method based on calculations over the field of 2 elements. This result translates to a result for the Euclidean question which is the best known but it is far from the conjecture. (It gives . ) This is essentially Frankl-Wilson’s theorem.
. ) This is essentially Frankl-Wilson’s theorem.
measure
One can try to discretize differently and use the polynomial methods for other fields and finding an appropriate “weighting” is indeed part of the difficulty but so far nobody managed to do it. There are promising competing methods which at present gives weaker bounds.
7 April, 2008 at 6:00 pm
Seva
Actually, why is “Kakeya only non-trivial in the regime when is fixed and
is fixed and  goes to infinity”? What is the smallest size of a subset of
goes to infinity”? What is the smallest size of a subset of  , containing a line in every direction? (The field
, containing a line in every direction? (The field 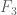 seems to be particularly interesting in this context as in this case the notion of a line is identical to that of a three-term arithmetic progression, not to mention that this is the first non-trivial case.) The trivial lower bound for the smallest size of such a set is
seems to be particularly interesting in this context as in this case the notion of a line is identical to that of a three-term arithmetic progression, not to mention that this is the first non-trivial case.) The trivial lower bound for the smallest size of such a set is  , and it seems that a random subset of $F_3^r$ of size at least
, and it seems that a random subset of $F_3^r$ of size at least  possesses the property in question with positive probability. Isn’t the gap between
possesses the property in question with positive probability. Isn’t the gap between  and
and  worth investigation?
worth investigation?
4 May, 2008 at 4:16 pm
Clifford Smyth
Hi,
What are some upper bounds on the minimum size of a Kakeya set in F_q^n?
I found one of size (q-1)^n + 2^n – 1. Surely there are smaller ones?
Cliff
8 May, 2008 at 6:49 am
Terence Tao
Dear Seva: You do have a point. Previous literature on the Kakeya problem did not seek to control the dependence of constants on the dimension, and so there were basically no interesting non-trivial results in the asymptotically high dimensional regime, but it is certainly possible to pose these questions in this regime. Very different techniques would probably be needed; in particular, in analogy with the Hales-Jewett theory, one might expect methods from ergodic theory to start playing some role. (In the F_3 case, it’s also possible, by analogy with the theory surrounding Roth’s theorem, that Fourier-analytic and additive-combinatorial techniques could also be effective.)
Dear Cliff,
In two dimensions, there are reasonably sharp results (giving sets close to q^2/2) in
http://arxiv.org/abs/math/0510356
http://arxiv.org/abs/math/0607734
(and see also a comment in
)
In higher dimensions, the best construction I know of uses the two-dimensional construction, combined with the trivial observation that the Cartesian product of two Kakeya sets is still a Kakeya set (in a higher dimensional space, of course). This gives about q^d / 2^{d/2} in the case when d is even, and slightly worse than this when d is odd. This is a fair distance away from Dvir’s bound, which is about q^d/d!. So there is still a little bit of room to close the gap here, and in particular to settle the question of whether the density of Kakeya sets needs to decay faster than exponentially (i.e. it is asymptotically less than c^d q^d as d -> infinity for any c > 0).
9 May, 2008 at 6:23 am
Simeon Ball
The bound in the two-dimensional case for q odd was recently improved to q(q+1)/2+(q-1)/2 by Blokhuis and Mazzocca.
This bound is tight as seen by the conic construction. Let C be a conic in PG(2,q), L the line at infinity, and m a bisecant to C (a line is incident with two points of the conic). Let E be the external points to C (which are the points that are incident with two tangents of C). Then the set
(E U C U m) \ L is a Kakeya (Besikovitch) set with q(q+1)/2+(q-1)/2 points.
Moreover, Blokhuis and Mazzocca have shown that all such sets that attain the bound come from this construction. The bound follows from an old result of Jamison. I have detailed this in
Click to access kakeya.pdf
To classify the sets meeting the bound, you use similar arguments to those used by Segre in the fifties to prove that a set of q+1 points in PG(2,q), q odd, with the property that every line is incident with at most two points of the set, is a conic. The proof of this has been done by Blokhuis and Mazzocca, although I’m not sure this preprint is available yet.
13 May, 2008 at 12:19 am
Simeon Ball
I forgot to mention in the previous post that L should be a tangent to C at a point P and that m is incident with P.
20 July, 2008 at 9:12 am
Francesco Mazzocca
The results by A.Blokhuis and F.Mazzocca about the finite Kakeya problem in two dimensional case, cited by Simeon Ball, will appear on the last volume of Bolyai Society Mathematical Studies dedicated to L.Lovász’s 60th birthday ( http://www.springer.com/math/numbers/book/978-3-540-85218-6?detailsPage=toc )
13 August, 2008 at 10:49 am
Plans and Updates « Combinatorics and more
[…] on the finite field Kakeya problem. The proof was extremely simple to start with (see Tao’s post ) and Zvi’s presentation was even simpler. It is a very interesting question how, given […]
27 November, 2008 at 3:36 pm
The Kakeya conjecture and the Ham Sandwich theorem « What’s new
[…] as a partial analogue of Dvir’s arguments in the finite field setting (which I discussed in this blog post) to the Euclidean setting; in particular, both arguments rely crucially on the ability to create a […]
9 December, 2008 at 7:25 am
mathaaron
some progresses toward these problems
http://arxiv.org/abs/0812.1043
17 December, 2008 at 3:10 pm
mike
Dr. tau,
have you seen Michael anthony’s solution to Riemann Hypothesis?
12 March, 2009 at 2:43 pm
The Kakeya set and maximal conjectures for algebraic varieties over finite fields « What’s new
[…] of Dvir and later authors on the Kakeya problem in finite fields, which I have discussed in this earlier blog post. Dvir established the following: Kakeya set conjecture for finite fields. Let F be a finite […]
11 May, 2009 at 10:49 am
Recent progress on the Kakeya conjecture « What’s new
[…] analogue of the low-degree algebraic geometry used in the incidence geometry approaches (see also this blog post for more discussion). Indeed, one can view Dvir’s argument in the incidence geometry […]
20 November, 2010 at 1:11 pm
The Guth-Katz bound on the Erdős distance problem « What’s new
[…] method (similar to, say, how Dvir proved the finite fields Kakeya conjecture, as discussed in this previous blog post). As such, the result in fact holds over an arbitrary field, but we will stick to for sake of […]
18 February, 2011 at 6:41 am
The Szemeredi-Trotter theorem via the polynomial ham sandwich theorem « What’s new
[…] arbitrary fields (not just over ), and can be proven by a simple linear algebra argument (see e.g. this previous blog post). However, the cell decomposition is more flexible than this algebraic fact due to the ability to […]
7 October, 2011 at 7:36 pm
On a short proof of Schwartz-Zippel lemma – Kenneth Shum's scrapbook
[…] by a solution to Kakeya set over finite field (see e.g. Terry Tao’s post), Dana Moshkovitz recently give an alternate proof of the Schwartz-Zippel lemma, (Schwartz-Zippel) […]
18 December, 2011 at 7:09 pm
“Kakeya sets over non-archimedean local rings,” by Dummit and Hablicsek « Quomodocumque
[…] this point, if you haven’t thought about the Kakeya conjecture before, you might want to read Terry’s long expository post about the Kakeya conjecture and Dvir’s theorem; I cannot do it any better […]
29 August, 2012 at 12:15 pm
Two Short Proofs of Hard Theorems « murphmath
[…] Terry Tao’s blog post […]
20 October, 2013 at 10:43 am
Punting in clearings of arbitrarily small Lebesgue measure | Complex Projective 4-Space
[…] a beautiful proof (which would certainly win Bradley’s elegance prize!), again mentioned in an article by Terry […]
25 October, 2013 at 7:48 am
Algebraic combinatorial geometry: the polynomial method in arithmetic combinatorics, incidence combinatorics, and number theory | What's new
[…] Alon is also another relatively early use of the polynomial method. More recently, it underlies Dvir’s proof of the Kakeya conjecture over finite fields and Guth and Katz’s near-complete solution to the Erdos distance problem in the plane, and […]
17 November, 2013 at 1:08 pm
Mohammad
Would you mind clarifying the following intuition ” …take advantage of the multiple scales available in the Euclidean setting” ?
17 May, 2016 at 6:36 pm
Ellenberg’s announcement of a solution to the cap-set problem | in theory
[…] that had resisted attacks from powerful Fourier-analytic proofs, and was solved by Zeev Dvir with a relatively simple application of the polynomial method. One may hope that the method has not yet exhausted its […]
18 May, 2016 at 12:13 am
A symmetric formulation of the Croot-Lev-Pach-Ellenberg-Gijswijt capset bound | What's new
[…] method in superficially similar problems such as the finite field Kakeya problem (discussed in this previous post), it was natural to wonder that this method could be applicable to the cap set problem (see for […]
9 September, 2016 at 9:48 am
Introduction to the polynomial method (and other similar things) | Short, Fat Matrices
[…] that this differs slightly from Terry Tao’s exposition.) To do this, we suppose to the contrary that . Then by the previous result, there exists a […]
18 March, 2020 at 2:40 am
Or Ordentlich, Oded Regev and Barak Weiss: New bounds for Covering Density! | Combinatorics and more
[…] aspect of the proof is the use of finite field Kakaya-type questions. Since the breakthrough by Zeev Dvir, many people had hopes for applications from the finite fields results to the Euclidean setting (in […]
4 December, 2021 at 9:30 pm
Kakeya 转针问题 & 何为维度 – 南外数学逻辑与生活社
[…] Dvir 对有限 Kakeya 问题的优美证明 — https://terrytao.wordpress.com/2008/03/24/dvirs-proof-of-the-finite-field-kakeya-conjecture/ […]
16 November, 2022 at 5:06 am
Barnabás Janzer: Rotation inside convex Kakeya sets | Combinatorics and more
[…] problem is the conjecture that every Kakeya set in has Housdorff dimension . in 2008, Zeev Dvir found a simple remarkable proof for a finite field analog of the conjecture. Finding possible connections between the finite field […]