Returning (perhaps anticlimactically) to the subject of the Poincaré conjecture, recall from Lecture 2 that one of the key pillars of the proof of that conjecture is the finite time extinction result (see Theorem 4 from that lecture), which asserted that if a compact Riemannian 3-manifold (M,g) was initially simply connected, then after a finite amount of time evolving via Ricci flow with surgery, the manifold will be empty.
In this lecture and the next few, we will describe some of the key ideas used to prove this theorem. We will not be able to completely establish this theorem at present, because we do not have a full definition of “surgery”, but we will be able to establish some partial results, and indicate (in informal terms) how to cope with the additional technicalities caused by the surgery procedure. Hopefully, if time permits later in the class, once we have studied the surgery process, I will be able to revisit this material and flesh out these technicalities a bit more.
The proof of finite time extinction proceeds in several stages. The first stage, which was already accomplished in the previous lecture (in the absence of surgery, at least), is to establish lower bounds on the least scalar curvature . The next stage, which we discuss in this lecture, is to show that the second homotopy group
of the manifold must become extinct in finite time, thus all immersed copies of the 2-sphere
in M(t) for sufficiently large t must be contractible to a point. The third stage is to show that the third homotopy group
also becomes extinct so that all immersed copies of the 3-sphere
in M are similarly contractible. The final stage, which uses homology theory, is to show that a non-empty 3-manifold cannot have
simultaneously trivial, thus yielding the desired claim (note that a simply connected manifold has trivial
by definition; also, from Exercise 2 of Lecture 2 we see that all components of M remain simply connected even after surgery).
More precisely, in this lecture we will discuss (most of) the proof of
Theorem 1. (Finite time extinction of ) Let
be a Ricci flow with surgery on compact 3-manifolds with
, with M(0) containing no embedded copy of
with trivial normal bundle. Then for all sufficiently large t,
is trivial (or more precisely, every connected component of M(t) has trivial
).
The technical assumption about having no copy of with trivial normal bundle is needed solely in order to apply the known existence theory for Ricci flow with surgery (see Theorem 2 from Lecture 2).
The intuition for this result is as follows. From the Gauss-Bonnet theorem (and the fact that the Euler characteristic of the sphere is positive), we know that 2-spheres tend to have positive (Gaussian) curvature on the average, which should make them shrink under Ricci flow. (Here I am conflating Gaussian curvature with Ricci curvature; however, by restricting to a special class of 2-spheres, namely minimal surfaces, one can connect the two notions of curvature to each other (and to scalar curvature) quite nicely.) On the other hand, the presence of negative scalar curvature can counteract this by expanding these spheres. But the lower bounds on scalar curvature tell us that the negativity of scalar curvature becomes weakened over time, and it turns out that the shrinkage caused by the Gauss-Bonnet theorem eventually dominates and sends the area of all minimal immersed 2-spheres into zero, at which point one can conclude the triviality of
by the Sacks-Uhlenbeck theory of minimal 2-spheres.
The arguments here are drawn from the book of Morgan-Tian and from the paper of Colding-Minicozzi. The idea of using minimal surfaces to force disappearance of various topological structures under Ricci flow originates with Hamilton (who used 2-torii instead of 2-spheres, but the idea is broadly the same).
— Curvature on surfaces —
We have seen how Riemannian manifolds have various notions of curvature: Riemannian curvature
, Ricci curvature
, and scalar curvature R. These are intrinsic notions of curvature: they depend only on the manifold M (and its metric g), and not how this manifold is embedded (if it is embedded at all) in some larger space. However, there are some important extrinsic notions of curvature as well, which describe how an immersed manifold
is curved inside its ambient space M. In particular, we will recall the Gauss curvature K, principal curvatures
, and mean curvature H of a surface (i.e. a 2-dimensional manifold)
inside a 3-manifold (M,g). [These notions can also be defined for other dimensions, but we will focus exclusively on the case of surfaces inside 3-manifolds.] We will also recall the standard fact that the mean curvature H vanishes whenever the surface is a minimal surface.
Let be an immersed 2-surface in a Riemannian 3-manifold
. All our computations here will be local, in the neighbourhood of some point
in
(and thus in M; in particular we can pretend that the immersed manifold
is in fact embedded as a submanifold of M. If we let h be the restriction of the metric
to
(restricting TM to
, etc.) then of course
is a Riemannian 2-manifold.
It is convenient to pick a unit normal vector field , thus n has norm 1 and is orthogonal to
at every point in
. It is only the value of n on the submanifold
which is important, but we will arbitrarily extend n smoothly to all of M so that we can take advantage of vector field operations on the ambient space. There is a choice of sign for n (e.g. if
bounded a three-dimensional region, we could pick either the outward or inward normal), which can lead to an ambiguity in sign in the principal and mean curvatures, but it will not affect the sign of the Gauss curvature.
Let be the Levi-Civita connection on M, and let X, Y be two vector fields which are tangential to
, thus
for all
. Then the covariant derivative
need not be tangential to
, but we can decompose
, (1)
where is the component of
parallel to n, and
is the component which is orthogonal to n (and in particular lies in
on
.
Exercise 1. Show that is the Levi-Civita connection on
, and that
(2)
on . (Hint: for the latter, compute the quantity
in two different ways.) Conclude that
can be identified with a symmetric rank (0,2) tensor (known as the second fundamental form) on
, which (up to sign) is independent of the choice of normal
.
Exercise 2. Using (1), deduce the Gauss equation
(3)
on , whenever X, Y, Z, W are vector fields that are tangent to
, and
and
are the Riemann curvature tensors of
and
respectively. (One could of course write (3) in abstract index notation, but we have chosen not to do so to avoid confusion between the two bundles
and
that are implicitly in play here.)
At any point , the second fundamental form
can be viewed as a symmetric bilinear form on the two-dimensional space
, which thus has two real eigenvalues
, known as the principal curvatures of
(as embedded in M) in x. The normalised trace
of the second fundamental form is known as the mean curvature. Meanwhile, the Gauss curvature K = K(x) at a point
is defined as equal to half the scalar curvature of
:
. (In particular, this manifestly demonstrates that the Gauss curvature K is intrinsic; this fact, combined with Exercise 3 below, is essentially the famous theorema egregium of Gauss.)
Exercise 3. Using Exercise 2, establish the identity
(4)
where is the sectional curvature of
in M, defined at a point x by the formula
where
are an orthonormal basis of
at x. In particular, if
is Euclidean space, then the Gauss curvature is just the product of the two principal curvatures (or equivalently, the determinant of the second fundamental form).
From (4) and the arithmetic mean-geometric mean inequality, we obtain in particular the following relationship between Gauss, mean, and sectional curvature:
. (5)
Next, we now recall a special case of the Gauss-Bonnet theorem.
Proposition 1. (Gauss-Bonnet theorem for ) Let
be an immersion of the sphere
, and let
be the Gauss curvature. Then
, where
is the volume measure (or area measure) associated to h.
Proof. We use a flow-based argument. Since Gauss curvature is intrinsic, we may pull back and assume that is in fact equal to
, but with some generic Riemannian metric which we shall call
, which may differ from the standard Riemannian metric on
, which we shall call
. We can flow from
to
by the linear flow
(say); note that this is a smooth flow on Riemannian metrics. Our task is to show that
at time zero. By equations (15), (19) of Lecture 1, we have
. (6)
The contribution of the second and third terms vanish thanks to Stokes’ theorem (equation (28) from Lecture 1). And in two dimensions, the Bianchi identities force the Ricci curvature to be conformal, i.e. it is equal to
. Thus the right-hand side of (6) vanishes completely, and so by the fundamental theorem of calculus, the value of
at time 0 is equal to that at time 1. The claim then follows from the standard facts that
with the usual metric has area
and constant scalar curvature +2 (or Gauss curvature +1).
From this and (5) we conclude that
(7)
for any immersed copy of . Thus we can start lower bounding sectional curvatures on the average, as soon as we figure out how to deal with the mean curvature H.
To do this, we now specialise to immersed spheres which are minimal; they have minimal area
with respect to smooth deformations. The following proposition is very well known:
Proposition 2. Let be a minimal immersed surface. Then the mean curvature H of
is identically zero.
Proof. Let us consider a local perturbation of . Working in local coordinates as before, we choose a unit normal field n, and flow
using the velocity field
, where f is a localised scalar function. This has the effect of deforming the metric h on
at the rate
, where
is the Lie derivative along the vector field Z. By equation (19) from Lecture 1, the area of
will thus change under this deformation at the rate
. (8)
On the other hand, as is minimal, the left-hand side vanishes. Also, using equation (25) from Lecture 1, we have
(9)
where X, Y is an orthonormal frame of (we can work locally, so as to avoid the topological obstruction of the hairy ball theorem). Expanding out
and recalling that n is orthogonal to X and Y, some calculation using (2) allows us to express (9) as
. (10)
Putting all this together, we conclude that for all local perturbations f, which implies that H vanishes identically.
It is an instructive exercise to try to convince oneself of the validity of Proposition 2 by pure geometric intuition regarding curvature and area.
From (7) and Proposition 2 we conclude a lower bound
(11)
for the integrated sectional curvature of a minimal immersed 2-sphere in a 3-manifold M.
— Minimal immersed spheres and Ricci flow —
Now let be a compact 3-manifold with a non-trivial second homotopy group
. Thus there exist immersions
which cannot be contracted to a point. It is a theorem of Sacks and Uhlenbeck that the area of such incontractible immersions cannot be arbitrarily small (for fixed M, g), and so if one defines
to be the infimum of the areas of all incontractible immersed spheres, then
is strictly positive.
It is a result of Meeks and Yau that the infimum here is actually attained, which would mean that there is a incontractible minimal immersed 2-sphere which has area exactly
. However, it suffices for our purposes to use a simpler result that an incontractible minimal 2-sphere
of area exactly
exists which is a branched immersion rather than an immersion, which roughly speaking means that there are a finite number of points in
where the function f behaves like an embedding of the power function
in the neighbourhood of the complex origin. See Lemma 18.10 of Morgan-Tian’s book for details (roughly, one needs to regularise the energy functional to obtain the Palais-Smale condition, then take limits to obtain a weak harmonic map, using a somewhat crude surgery argument to show that bubbling does not occur in the minimum area limit). For simplicity we shall ignore the effects of branching here; basically, branch points increase the integrated Gauss curvature in the Gauss-Bonnet theorem, but this effect turns out to have a favourable sign and is thus ultimately harmless.
Now suppose that is a Ricci flow for t in some time interval I. Suppose that t lies in I but is not the right endpoint of I. Then we have an incontractible minimal 2-sphere
of area
which is a branched immersion; we will suppose that it is an immersion for simplicity. Let us now see how the area
of
changes under Ricci flow. Using the variation formula (19) for the 2-dimensional measure
, specialised to Ricci flow, we have
(12)
where is the Ricci curvature of the 3-manifold M, and h is the 2-dimensional metric formed by restricting g to
. We now apply the following identity:
Exercise 4. Show that , where
is the sectional curvature of
and
is the scalar curvature of M. (Hint: use two tangent vectors of
and one normal vector to build an orthonormal basis, and write the Ricci and scalar curvatures in terms of sectional curvatures.)
Inserting this identity into (12) and using (11), as well as the lower bound , we conclude that
; (13)
by definition of , we thus conclude the ordinary differential inequality
(14)
in the sense of forward difference quotients.
This is already enough to obtain a weak version of Theorem 1:
Theorem 2. (Non-trivial implies finite time singularity) Let
be a Ricci flow on a time interval [0,T) for a compact 3-manifold with
non-trivial. Then T must be finite.
Proof. At time zero, the minimal scalar curvature is of course finite. By rescaling if necessary we may assume
(say). Then Proposition 2 of Lecture 3 implies that
, and so from (14) we have
. (15)
This can be rewritten (by the usual method of integrating factors) as
. (16)
Now, the expression is divergent when integrated from zero to infinity, while the expression
is finite and non-negative. These two facts contradict each other if T is infinite, and so T is finite as claimed.
Note that this argument in fact gives an explicit upper bound for the time of development of the first singularity, in terms of the minimal Ricci curvature at time zero and minimal area of an immersed sphere at time zero.
We now briefly discuss how the same arguments can be extended to tackle Ricci flow with surgery, though this discussion will have to be somewhat informal since we have not yet fully defined what surgery is. The basic idea is to ensure that the inequality (14) persists through surgery. In a little more detail, the argument proceeds as follows:
- The first step is to clarify the topological nature of the surgery. It turns out that at each surgery time t, the manifold
can be obtained (in the topological category) from
by finding a collection of disjoint 2-spheres in
, performing surgery on each 2-sphere to replace it with a pair of disks, then removing all but finitely many of the connected components that are created as a consequence.
- At any given time t, let s(t) denote the maximal number of embedded 2-spheres one can place in
which are homotopically essential in the sense that none of these spheres can be contracted to a point, or deformed to any other sphere. It is possible to use homological arguments and van Kampen’s theorem to show that s(t) is always finite.
- By homotopy theory, one can show that every time a surgery involves at least one homotopically essential sphere, the quantity s(t) decreases by at least one. Thus, after a finite number of surgeries, all spheres involved in surgery are contractible to a point. By shifting the time variable if necessary, we may thus assume that the above claim is true for all times
.
- Once all spheres involved in surgery are contractible, one can show that whenever surgery is applied to a connected manifold, either the manifold is removed completely, or one of the post-surgery components is homotopy equivalent to the original manifold, and the rest are homotopy spheres. In particular, if a connected manifold has non-trivial
before surgery, then it is either removed by surgery, or one of the post-surgery components has the same
; and if a connected manifold has trivial
then all post-surgery components do also. Thus if Theorem 1 fails, one can find a “path of components” through the Ricci flow with surgery with non-trivial
for all time. We now restrict attention to this path of components, which by abuse of notation we shall continue to call M(t) at each time t.
- Using the geometric properties of the surgery and standard limiting arguments, we can show that if
is non-positive before surgery, then it cannot decrease as a consequence of surgery (thus
, and similarly if
is non-negative before surgery, then it stays non-negative after surgery (here we adopt the convention that
when the manifold is empty). These facts are ultimately because surgery is only performed in regions of high positive curvature. From this, one can conclude (assuming the initial normalisation
that the bound
persists even after surgery.
- Finally, using the geometric properties of the surgery and standard limiting arguments, one can show that
has no upward jump discontinuity at surgery times t in the sense that
. This allows us to repeat the proof of Theorem 2 and obtain the desired contradiction to prove Theorem 1.
Further details can be found in Section 18.12 of Morgan-Tian’s book, and I will hopefully return to this matter later in the course.
[Update, April 13: minor corrections.]
[Update, April 15: Condition about no embedded with trivial normal bundle added.]
[Update, April 17: Behaviour of with respect to surgery clarified.]
[Update, May 7: Meeks-Yau reference added; thanks to Sylvain Maillot for this correction (as well as various corrections to other lectures).]

13 comments
Comments feed for this article
12 April, 2008 at 4:38 am
fedfan
A slightly off topic question Professor Tao: what references do you suggest
for the basic theory of Riemannian manifolds?
12 April, 2008 at 7:11 am
wenwen
Dear Terry,
Some possible typo s:
1. 3rd line of the proof of Prop2, h^\dot =L_Z g instead of h^\dot =L_X g
2. 4th line of the proof of Prop2, By equation (19) instead of (15)
One question about theorem 2 is that, for Sacks-Uhlenbeck, we don’t need a vanishing \pi_2 to construct minimal branched sphere. So can we remove this assumption in theorem 2?
12 April, 2008 at 11:47 pm
Andy Sanders
Prof Tao,
Just a quick typo, in the proof of theorem 2 I think you want to say, “These two facts contradict….” But I find myself significantly more confused by what this contradiction is. It seems that none of the expressions on the right hand sides, (15) and what follows, are non-negative. Could you clarify the conclusion of this proof?
On another note, I’m curious where you found this nice analytic proof of Gauss Bonnet for S^2. It appears to be genuinely different, in quite a pretty and concise way, than other proofs I have seen.
Thanks,
Andy
13 April, 2008 at 1:05 pm
Terence Tao
Dear all: thanks for the corrections! (There was a bizarre formatting error in Theorem 2 that was making it read strangely, but it’s finally fixed now.)
As for the analytic proof of Gauss-Bonnet, I’m sure it must be folklore, but I simply computed the first variation (i.e. the derivative) of the expression (which, a fortiori, must vanish if Gauss-Bonnet is true), and indeed everything canceled out (as it must). More generally, the trick of proving an integral identity by taking a first variation tends to reduce matters (after doing all the obvious integration by parts) to establishing a pointwise identity, which can usually be verified in finite time by pure algebra (assuming that the integrand consisted entirely of local terms, and that there are no ambient constraint equations).
(which, a fortiori, must vanish if Gauss-Bonnet is true), and indeed everything canceled out (as it must). More generally, the trick of proving an integral identity by taking a first variation tends to reduce matters (after doing all the obvious integration by parts) to establishing a pointwise identity, which can usually be verified in finite time by pure algebra (assuming that the integrand consisted entirely of local terms, and that there are no ambient constraint equations).
As for books, I am using Petersen’s “Riemannian Geometry”, though I am somewhat biased because I have the advantage of having Peter Petersen sitting in my class to answer questions as I teach this course. I also have profitably used Chavel’s book and Jost’s book in the past, as well as some general relativity texts that also cover (pseudo-)Riemannian geometry, though I am not relying on them currently.
As for the question about trivial , I would believe in this case that there might not be any non-trivial minimal spheres; as far as I am aware, Sacks-Uhlenbeck theory only applies to spheres that are not contractible to a point, and of course such spheres do not exist when
, I would believe in this case that there might not be any non-trivial minimal spheres; as far as I am aware, Sacks-Uhlenbeck theory only applies to spheres that are not contractible to a point, and of course such spheres do not exist when 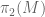 is trivial.
is trivial.
13 April, 2008 at 4:37 pm
wenwen
In fact, the Sacks-Uhlenbeck stuff works for trivial . For example, let’s take
. For example, let’s take 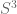 (we know
(we know  . But the standard embedding of
. But the standard embedding of 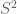 is a “maximal” sphere (so is minimal).
is a “maximal” sphere (so is minimal).
13 April, 2008 at 9:06 pm
Andy Sanders
Thanks for the clarifications.
15 April, 2008 at 10:30 pm
285G, Lecture 5: Finite time extinction of the third homotopy group, I. « What’s new
[…] the previous lecture, we saw that Ricci flow with surgery ensures that the second homotopy group became extinct in […]
15 April, 2008 at 10:34 pm
Terence Tao
Dear wenwen,
Ah, now I see what you’re saying. (I was thinking of “minimal surface” as necessarily being a local minimiser of the area functional, when instead it is usually defined as merely being a critical point of that functional, i.e. zero mean curvature.) The key inequality (13) still holds for such surfaces, but it does not lead to the inequality (14) for the width functional . However, one can use (13) for such surfaces to obtain a similar inequality for another width functional
. However, one can use (13) for such surfaces to obtain a similar inequality for another width functional  , which is defined whenever one has non-trivial
, which is defined whenever one has non-trivial  (rather than non-trivial
(rather than non-trivial  ); this is discussed in the Lecture 5 notes which I’ve just uploaded.
); this is discussed in the Lecture 5 notes which I’ve just uploaded.
18 April, 2008 at 11:48 am
285G, Lecture 6: Finite time extinction of the third homotopy group, II « What’s new
[…] Lecture 4, we studied minimal immersed spheres into a three-manifold, and how their area varied with respect […]
21 April, 2008 at 11:52 am
285G, Lecture 7: Rescaling of Ricci flows and kappa-noncollapsing « What’s new
[…] 2 and are also supercritical. Thus the various bounds we have on these quantities from Lectures 4, 5, 6 do not directly tell us anything about asymptotic […]
24 April, 2008 at 4:34 pm
285A, Lecture 8: Ricci flow as a gradient flow, log-Sobolev inequalities, and Perelman entropy « What’s new
[…] (we have already exploited this fact to prove the Gauss-Bonnet formula, see Proposition 1 from Lecture 4). More generally, we recover see from (10) the fact (well known in general relativity) that the […]
30 May, 2008 at 10:24 pm
285G, Lecture 16: Classification of asymptotic gradient shrinking solitons « What’s new
[…] 1 near infinity. But this means that , contradicting the Gauss-Bonnet formula (Proposition 1 from Lecture 4). Thus Case 3 cannot in fact […]
2 June, 2008 at 1:15 pm
285G, Lecture 17: The structure of κ-solutions « What’s new
[…] to be instead of the quotient . Then we observe from the Gauss-Bonnet theorem (Proposition 1 from Lecture 4) that , and hence by the volume variation formula (equation (33) from Lecture 1) the volume is […]